# 1988：記憶的兩個組成成分 [TOC=2,5] [長期記憶的雙組分模型](https://supermemo.guru/wiki/Two-component_model_of_long-term_memory)是 [SuperMemo](https://supermemo.guru/wiki/SuperMemo) 的基礎，并在 [SM-17 算法](https://supermemo.guru/wiki/Algorithm_SM-17)中明確表示。它區分了知識在長期記憶存儲中的穩定性和提取的難易程度。這仍然是學習理論中一個鮮為人知的典型事實，即一個人可以流利，但記憶力仍然很差。 從長遠來看，流利度并不能很好地衡量學習效果。 ## 長期記憶的組成成分 多年來，記憶研究人員一直使用“記憶強度”這個詞。它應該反映出人們對事物的記憶有多好。 上世紀 80 年代中期，我對[間隔重復](https://supermemo.guru/wiki/Spaced_repetition)的研究讓我很快意識到，一個*強度*變量不足以描述存儲在長期記憶中的知識的狀態。我們需要兩個變量來區分事實從記憶中提取的難易程度。 我的結論是，存儲在長期記憶中的知識的狀態可以用兩個變量來描述：[穩定性](https://supermemo.guru/wiki/Stability)和[可提取性](https://supermemo.guru/wiki/Retrievability)。記憶的穩定性告訴您記憶在存儲中可以持續多長時間。可提取性告訴你回憶一段知識是多么容易。在記憶研究中，這兩個變量常常被混為一談。 令人驚訝的是，在我觀察了三十年之后，記憶的兩個組成成分的概念仍然在滲透主流的記憶研究。2018 年，大多數論文忽略了這兩個變量的分離，仍然依賴于單一的“記憶強度”概念。這導致了巨大的困惑和研究進展緩慢。 ## 記憶雙組分模型的起源 1988 年 1 月 9 日，我在計算機模擬課上的一篇論文中首次描述了[長期記憶的兩個組成成分](https://supermemo.guru/wiki/Two_component_model_of_memory)。在同一篇論文中，我用了一種不相關的推理方法，得出結論：[陳述性學習](https://supermemo.guru/wiki/programural_learning)和[過程性學習](https://supermemo.guru/wiki/programural_learning)一定涉及不同的回路。 如果您停下來思考一分鐘，那么雙組分的整個思想應該是非常顯然的。如果你在復習后馬上取兩段記憶，一段最佳時間間隔很短，另一段最佳時間間隔很長，那么這兩段記憶的記憶狀態必然不同。兩者都可以被完美地回憶(最大的可提取性)，它們還需要在記憶中持續的時間上有所不同(不同的穩定性)。我很驚訝我找不到任何關于這個主題的文獻。然而，如果文獻中沒有提及在間隔重復中存在最優間隔，那么這個看似明顯的結論可能隱藏在另一個看似明顯的概念背后：在最優間隔復習中間隔遞增的級數。這是一個可愛的例子，說明人類的進步是漸進的，而且緩慢得令人痛苦。我們是出了名的不善于創新。燭臺下最暗。這一弱點可以通過網絡交流的爆炸來打破。我主張少一些同行審查，多一些大膽的假設。我提到了 Robin Clarke 關于阿爾茨海默病的論文中的一個很好的例子。嚴格的同行審查讓人想起普魯士的學校教育：在追求完美的過程中，我們失去了創造力，失去了人性，最終失去了生活的樂趣。 1988 年 2 月 19 日，當我第一次向我的老師 Katulski 博士提出我的想法時，他并沒有給我留下太深刻的印象，但他給了我一張計算機模擬學分的通行證。順便說一句，不久之后，Katulski 成為 [SuperMemo 1.0 for DOS](https://supermemo.guru/wiki/SuperMemo_1.0_for_DOS) 的首批用戶之一。 在我的[碩士論文](https://supermemo.guru/wiki/Master's_Thesis)(1990)中，我添加了一個稍微正式的證明，證明這兩個組件的存在(參見[下一節](https://supermemo.guru/wiki/History_of_spaced_repetition_(print)#Proof))。我論文的那一部分沒有引起注意。 1994年，J.Kowalski 在波蘭恩特寫道： > 我們已經到了這樣一個階段，對記憶的進化解釋表明，它使用的原理是增加間隔和[間隔效應](https://supermemo.guru/wiki/Spacing_effect)。除了進化論的推測外，還有什么證據可以證明這種記憶模型嗎？在他的博士論文中，Wozniak 廣泛地討論了記憶的分子層面，并提出了一個假設模型，描述了學習過程中突觸發生的變化。本文提出的新元素是記憶痕跡的[穩定性](https://supermemo.guru/wiki/Stability)和[可提取性](https://supermemo.guru/wiki/Retrievability)之間的區別。這不能用來支持 [SuperMemo](https://supermemo.guru/wiki/SuperMemo) 的有效性，因為一個簡單的事實是，正是 SuperMemo 本身奠定了假設的基礎。然而，越來越多的分子層面證據似乎與穩定性-可提取性模型相吻合，同時，該模型為導向 SuperMemo 的假設的正確性提供了支持。簡單地說，可提取性是記憶的一種屬性，它決定了突觸對刺激反應的效率水平，從而引發學習行為。可提取性越低，您就越不可能回憶起對問題的正確回答。另一方面，穩定性反映了早期重復的歷史，并決定了記憶痕跡能夠維持的時間范圍。記憶的穩定性越高，可提取性下降到零，即下降到記憶永久遺忘所需的時間就越長。根據 Wozniak 的說法，當我們第一次學習某樣東西的時候，我們會在編碼特定刺激反應關聯的突觸中體驗到穩定性和可提取性的輕微提高。隨著時間的推移，可提取性迅速下降；相當于遺忘的現象。同時，記憶的穩定性保持在大致相同的水平。然而，如果我們在可提取性下降到零之前重復這種關聯，可提取性將恢復其初始值，而穩定性將增加到一個新的水平，顯著高于初次學習時的水平。在下一次重復發生之前，由于穩定性的提高，可提取性以較慢的速度下降，在遺忘發生之前，重復之間的間隔可能要長得多。記憶的另外兩個重要特性也應該注意到：(1) 當可提取性高時，重復不能增加穩定性(間隔效應)，(2) 遺忘時，穩定性迅速下降 ## 同行評議刊物 (1995) 我們與 [Janusz Murakowski 博士](https://supermemo.guru/wiki/Janusz_Murakowski)和 [Edward Gorzelanczyk 博士](https://supermemo.guru/wiki/Edward_Gorzelanczyk) 在 [1995](http://supermemory.com/english/2vm.htm) 發表了我們的想法。Murakowski 完善了數學證明。Gorzelanczyk 充實了分子模型。我們沒有從科學界聽到太多的熱情和反饋。記憶的兩個組成成分的概念就像葡萄酒，時間越久，味道就越好。我們一直想知道它什么時候會得到更廣泛的認可。畢竟，我們并不是生活在[孟德爾](https://en.wikipedia.org/wiki/Gregor_Mendel)的時代，把一塊好寶石藏在某個晦澀的檔案中。間隔重復的用戶數以百萬計，即使只有 0.1% 的人對這個理論感興趣，他們也會聽說我們的兩個組分。今天，甚至 [SuperMemo](https://supermemo.guru/wiki/Algorithm_SM-17) 中的[最新算法](https://supermemo.guru/wiki/SuperMemo)都是基于雙組分模型的，而且運行起來很有魅力。具有諷刺意味的是，用戶往往會涌向[更簡單的解決方案](https://supermemo.guru/wiki/Algorithm_SM-2)，那里隱藏著人類記憶的所有機制。即使在 [supermemo.com](http://supermemo.com/) 上，我們也確保不會用屏幕上過多的數字嚇到客戶。這樣，我們就可以在渴望簡單的用戶中更好地采用模型的指導功能。 ## Robert Bjork 的研究 記憶的兩個組成成分的概念在以前的研究中有相似之處，特別是在 [Bjork](https://supermemo.guru/wiki/Bjork) 的研究中。 在 20 世紀 40 年代，科學家研究了習慣強度和反應強度作為老鼠行為的獨立組成部分。這些概念后來在 Bjork 的廢用理論中重新表述。Herbert Simon 在 1966 年的論文中似乎注意到了記憶穩定性變量的必要性。1969 年，Robert Bjork 提出了強度悖論：回憶的概率和復習的記憶效果之間存在反向關系。請注意，他的是根據兩分量模型對間隔效應的重述，這距離闡明記憶變量之間的區別只有一小步之遙。這引出了 Bjork 的新廢用理論(1992)，該理論區分了儲存強度和提取強度。這是與可提取性和穩定性相近的等價物，但對作為區別基礎的機制的解釋略有不同。最引人注目的是，Bjork 認為，當可提取性降至零時，仍然保留了穩定的記憶(在我們的模型中，穩定性變得不確定)。在細胞層面上，Bjork 可能是對的，至少在一段時間內是正確的，但實踐 SuperMemo 顯示了完全遺忘的力量，而從神經的角度來看，保留廢棄的記憶將是非常低效的，獨立于它們的穩定性。最后但并非最不重要的一點是，Bjork 用連接性來定義存儲強度，這與我認為優秀學生身上會發生的事情非常接近：一致性會影響穩定性。 為什么記憶的兩個組成成分還沒有進入主流研究？我認為，如果人類的思維傾向于短視，而我們都是故意的，那么科學的頭腦可能真的會被繁重的職責、發表或滅亡、撥款之爭、等級制度、利益沖突、同行評議、教學義務，甚至行為準則扼殺。記憶研究人員傾向于生活在“記憶強度”的單一維度中。在這個維度上，他們不能真正理解需要研究以解決問題的分子和神經過程的真實動力學。具有諷刺意味的是，進步可能來自那些傾向于從事人工智能或神經網絡工作的人。Demis Hassabis 或 Andreas Knoblauch 的驚人頭腦通過獨立的推理過程、模型和模擬提出了兩個想法。生物學家將需要聆聽數學和計算機科學的語言。 ## 算法 SM-17 中的雙組分模型 [長期記憶的雙組分模型](https://supermemo.guru/wiki/Two_component_model_of_long-term_memory)是 [Algorithm SM-17](https://supermemo.guru/wiki/Algorithm_SM-17) 的基礎。算法 SM-17 的成功，是該模型正確性的最終實踐證明。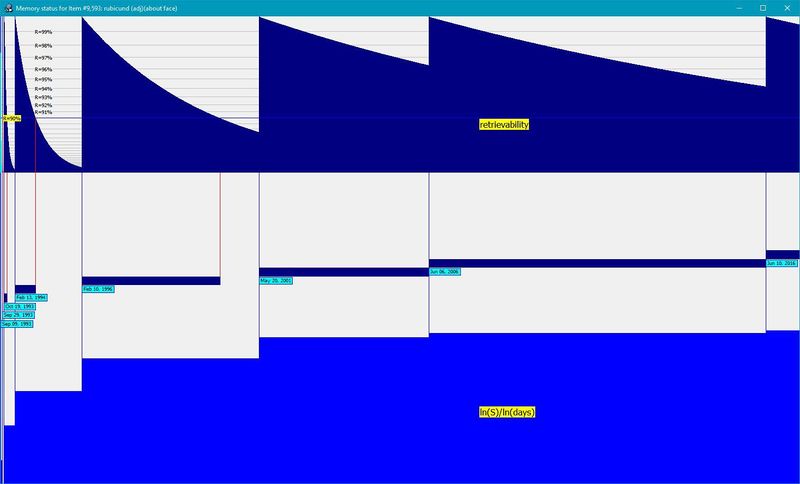 記憶的兩個組成成分的值的實際變化圖提供了記憶狀態演變的概念性可視化： [](https://supermemo.guru/wiki/File:Memory_status.jpg) > **圖：** 記憶狀態隨著時間的推移而發生變化。橫軸表示跨越整個重復歷史的時間。頂部面板顯示可提取性(十次冪，`$ R^{10} $`，便于分析)。灰色網格的可提取性指標分別為 R=99%、R=98% 等。中間深藍色的面板顯示的最佳間隔。重復日期用藍色豎線標記，并以淺藍綠色標記。當 R 越過 90% 線時，最佳區間的末端用紅色豎線表示(僅當區間大于最佳區間時)。下面板顯示穩定性(以 `$ \ln(S)/\ln(days) $` 表示，便于分析)。從圖中可以看出，當穩定性較低時，早期重復后的可提取性下降較快(指數級)，但在第 7 次復習后的 10 年時間里，可提取性僅從100%下降到 94%。所有的值都來自一個實際的重復歷史和記憶的三組分模型。 因為一個現實生活中的應用 [SuperMemo](https://supermemo.guru/wiki/SuperMemo) 需要解決不同難度的學習材料，模型中所涉及的第三個變[項目難度](https://supermemo.guru/wiki/Item_difficulty) (D)。項目難度的一些影響也已經在這篇[文章](https://supermemo.guru/wiki/History_of_spaced_repetition)被討論。特別是具有不同子成分的復合記憶對記憶穩定性的影響。 為了實現新的算法，我們定義了記憶的三個組成成分如下: - 記憶穩定性(S)被定義為在復習時產生 0.9 的平均回憶概率的重復間隔。 - 記憶可提取性(R)被定義為在假設同質學習材料按負指數函數遺忘的前提下，任意時刻的期望回憶概率，衰減常數由記憶穩定性(S)決定 - 項目難度(D)定義為復習時記憶穩定性(S)可能增加的最大值，線性映射到 0..1 區間，0 代表最容易的可能項目，1 代表 SuperMemo 中考慮的最高難度(目前的截止極限是穩定性增加 6 倍于記錄的最大值) ## 證明 下面是我碩士論文中的實際證明。這些語言和模型已經有 30 年的歷史了，而且有些笨拙。然而，核心思想至今仍然站得住腳。要更好地理解證明，請參見 Murakowski 的證明。 > 檔案警告：為什么要使用文字檔案？ > > 這篇文章是：“優化學習” (1990) [Piotr Wozniak](https://supermemo.guru/wiki/Piotr_Wozniak) 的一部分 > > ### 10.4.2. 記憶的兩個變量：穩定性和可提取性 > > 有一個重要的結論直接來自于 SuperMemo 理論，那就是有兩個變量，而不是像人們通常認為的一個描述突觸電導率和一般記憶的變量。為了說明這種情況，讓我們再次考慮突觸記憶的 calpain 模型。從模型中可以明顯看出，它的作者假設只需要一個自變量來描述突觸的傳導性。鈣的內流、鈣蛋白酶的活性、食物蛋白的降解和谷氨酸受體的數量都是這種變量的例子。請注意，所有提到的參數都是相關的，即知道其中一個參數，我們可以計算所有其他參數；顯然，只有在能夠構造相關公式的情況下才能計算。參數的依賴性是它們之間因果聯系的直接結果。 > > 然而，最佳學習過程恰好需要兩個獨立變量來描述給定時刻突觸的狀態： > > - 起時鐘作用的變量，用于測量兩次重復之間的時間。這里可以使用的示例性參數包括： > - `$ T_e $` - 自上次重復以來已經過去的時間（屬于區間 <0，最佳間隔>）， > - `$ T_L $` - 在下一次重復發生之前必須經過的時間（`$ T_L $` = 最佳間隔 - `$ T_e $`）， > - `$ P_f $` - 突觸在有問題的一天內丟失記憶痕跡的概率（屬于區間 <0，1>）。 > - 衡量記憶持久性的變量。這里可以使用的示例性參數包括： > - I(n+1) - 在下一次重復之后應該使用的最佳間隔（I(n+1)=I(n)*C，其中 C 是大于 3 的常數）， > - I(n) - 現在的最佳間隔 > - n - 在回答問題的時刻之前重復的次數等。 > > 現在讓我們看看上述變量是否充分必要地描述突觸在時間最優學習過程中的狀態。為了說明變量是相互獨立的，我們將說明它們之間沒有一個可以相互計算。讓我們注意到，在給定的重復間隔內，I(n) 參數保持不變，而 `$ T_e $` 參數從 0 變為 I(n)。這表明沒有滿足條件的函數 f： > > > `$ T_e=f(I(n)) $` > > 另一方面，在隨后的重復時刻，`$ T_e $` 總是等于零，而 I(n) 總是有一個不同的、遞增的值。因此，不存在滿足條件的函數 g： > > > `$ I(n)=g(T_e) $` > > 因此 I(n) 和 `$ T_e $` 是獨立的。 > > 為了說明在最優學習過程中不需要其他變量，讓我們注意到，在任何給定時間，我們都可以使用下面的算法計算未來重復的所有時刻: > > 1. 經過 I(n) -`$ T_e $` 天 > 2. 讓我們重復一遍。 > 3. 令 `$ T_e $` 為零，I(n) 增加 C 倍。 > 4. 回到 1。 > > 請注意，對于給定的突觸，C 的值是一個恒定的特征，因此在學習過程中不會改變。稍后我將使用術語**可提取性**來表示第一個變量，使用術語**穩定性**來表示第二個變量。為了證明第一個學期的選擇是合理的，讓我注意到，我們過去常常認為記憶在學習任務之后是強烈的，然后它們就會消失，直到它們變得不再可以找回。這是決定記憶何時不再存在的可提取性。還值得一提的是，可提取性是被默認為唯一需要描述記憶的變量(就像在 calain 模型中一樣)。穩定性變量的不可見性是因為研究人員將精力集中在單一的學習任務和觀察突觸的后續變化上，而穩定性的重要性只有在多次重復同一任務的過程中才能可視化。為了總結對記憶變量的分析，讓我們提出在開發任何生物模型時必須提出的標準問題。記憶的兩個變量的存在可能產生的進化優勢是什么？ > > 可提取性和穩定性對于編寫一個學習過程的代碼都是必要的，該學習過程允許隨后的重復間隔在不遺忘的情況下增加長度。很容易證明，就個人的存活率而言，這種學習模式是最好的，如果我們承認這樣一個事實，即記住而不遺忘會在短時間內阻塞有限的記憶系統。如果記憶是健忘的，它必須有一種方法來保留這些似乎對生存很重要的痕跡。重復作為一種增強記憶的因素就是這樣一種方法。現在讓我們考慮一下重復過程的最合適時機是什么。如果一個給定的現象出現 n 次，那么它出現 n+1 次的可能性就會增加，因此更長的記憶保留時間似乎是有利的。描述最佳重復過程的確切函數取決于記憶存儲的大小、個人可能遇到的現象的數量以及許多其他因素。然而，通過重復記憶來維持記憶所需要的時間間隔的增加，以及記憶的可提取性和穩定性的進化價值，都是無可爭議的。我們可以想象，在進化過程中，許多情況都會干擾記憶發展的簡單圖景。例如，與強烈壓力相關的事件應該被更好地記住。事實上，兒茶酚胺對學習影響的研究證實了這一點。也許，使用荷爾蒙刺激可以提高應用 SuperMemo 方法的學生的表現。 > > **臨時摘要** > > 1. 假設存在描述最優學習過程所需的兩個自變量。這些變量被命名為記憶的可提取性和穩定性 > 2. 記憶的可提取性反映了重復之間的時間間隔，并指示記憶痕跡在回憶過程中能在多大程度上被成功利用 > 3. 記憶的穩定性反映了學習過程中重復的歷史，并且隨著突觸的每一次刺激而增加。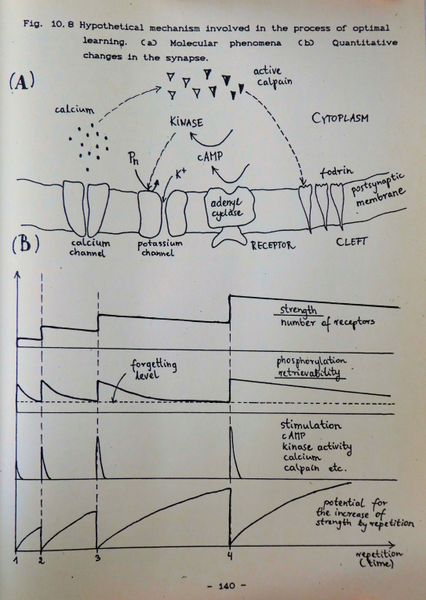它確定最佳重復間隔的長度 > > [](https://supermemo.guru/wiki/File:Hypothetical_mechanism_involved_in_the_process_of_optimal_learning.jpg) > > > **圖：** 在我的碩士論文“優化學習”(1990)中，我提出了一些假設概念，這些概念可能是基于間隔重復的優化學習過程的基礎。(A)分子現象 (B)突觸的數量變化。這些觀點在今天看來有些過時，但代表記憶可提取性的鋸齒形曲線在有關間隔重復的流行出版物中得到了廣泛的認識。它們通常被錯誤地歸因于赫爾曼?艾賓浩斯 > ## Murakowski 的證明 這里有一份由 [Murakowski](https://supermemo.guru/wiki/Janusz_Murakowski) 提交的證明： > 在早期的研究中已經發現，配對聯想學習中的最佳重復間隔，理解為需要最小重復次數才能無限期地保持恒定的知識保持水平(例如 95%)的間隔，可以用以下公式大致表示([Wozniak 和 Gorzelanczyk，1994](https://supermemo.guru/wiki/Optimization_of_repetition_spacing_in_the_practice_of_learning))： > > - (1) `$ I_1=C_1 $` > - (2) `$ I_i=I_{i-1}*C_2 $` > > 這里： > > - `$ I_i $` - 第 i 次重復后的重復間隔。 > - `$ C_1 $` - 第一個間隔的長度(取決于所選的知識保留，通常等于幾天)。 > - `$ C_2 $` - 常數，表示后續重復中重復間隔的增加(取決于所選的知識記憶和記憶項目的難度) > > 上述公式是使用計算機優化過程為人類受試者找到的，該計算機優化過程使用主動回憶丟棄技術來監督單詞對的自定步速學習過程。[...] > > 如下所示，被廣泛研究的記憶強度(或突觸增強)不足以解釋最佳重復間隔的規律：*[...]* > > 1. 我們想要確定存儲記憶痕跡所涉及的(分子)變量集，這些變量足以說明最佳重復間隔。首先，讓我們假設這些變量在學習中的兩個相關性，它們受制于公式(1)及(2)所表示的最佳間距： > > `$ r $` - 從當前時刻到當前最佳間隔結束的剩余時間(最佳間隔是指保留率在結束時降至先前定義的水平的間隔，例如 95%)。 > > `$ s $` - 當前最佳間隔的長度。 > > 2. 僅在第 i 次重復開始時，`$ r=0 $`，而 `$ s_i>s_{i-1}>0 $` (`$ s_i $` 表示正好在第 i 次重復開始時的 `$ s $`)。這表明沒有函數 `$ g_1 $` 使得 `$ s=g_1(R) $`，即 `$ s $` 不能只是 `$ r $` 的函數。 > > 3. 在重復間隔期間，`$ r(t_1)<>r(t_2) $` 當 `$ t_1<>t_2 $` (`$ t $` 表示時間，`$ r(t) $` 表示時刻 `$ t $`)。另一方面，`$ s(t_1)=s(t_2) $` (`$ s(t) $` 表示此時的 `$ s $`)。這表明不存在函數 `$ g_2 $` 使得 `$ r=g_2(s) $`，否則我們將有：`$ r(t_1)=g_2(s(t_1))=g_2(s(t_2))=r(t_2) $`，這導致了一個矛盾。`$ r $` 不能僅是 `$ s $` 的函數。 > > 4. 在步驟 2 和 3 中，我們已經證明了 `$ r $` 和 `$ s $` 是獨立的，因為沒有函數 `$ g_1 $` 和 `$ g_2 $` 使得 `$ s=g_1(r) $` 或 `$ r=g_2(s) $`。這顯然不意味著沒有參數 `$ x $` 和函數 `$ y_s $` 和 `$ y_r $` 使得 `$ s=y_s(x) $` 和 `$ r=y_r(x) $`。 > > 5. 可以看出，`$ r $` 和 `$ s $` 足以計算最佳重復間隔(參見公式(1)及(2))。讓我們首先假設以下兩個函數 `$ f_r $` 和 `$ f_s $` 在 s 涉及記憶存儲 i 的系統中是已知的：`$ r_i=f_r(s_i) $` 和 `$ s_i=f_s(s_{i-1}) $`。在我們的例子中，這些函數具有平凡的形式 `$ f_r：r_i=s_i $` 和 `$ f_s：s_i=s_{i-1}*C_2 $` (其中 `$ C_2 $` 是公式(2)中的常量。在這種情況下，變量 `$ r $` 和 `$ s $` 足以在任何時刻 `$ t $` 以最佳重復間隔表示記憶。以下是重復間隔算法，它表明這是正確的： > > 1. 假設變量 `$ r_i $` 和 `$ s_i $` 描述第 i 次重復后的記憶狀態 > 2. 時間流逝 `$ r_i $` > 3. 開始重復 > 4. 讓函數 `$ f_s $` 用于從 `$ s_i $` 計算新值 `$ s_{i+1} $` > 5. 讓函數 `$ f_r $` 用于從 `$ s_{i+1} $` 計算新值 `$ r_{i+1} $` > 6. `$ i:=i+1 $` > 7. 回到 2 > > 上述推理表明，變量 r 和 s 形成了計算最佳重復間隔所需的足夠的自變量集合。顯然，使用形式為 `$ r’’=Tr(r’) $` 和 `$ s’’=Ts(s’) $` 的一組變換函數，可以設想可以描述記憶系統狀態的變量對 r-s 的無窮族。一個困難的選擇仍然是選擇這樣一對 r-s，它將最方便地與突觸水平上發生的分子現象相對應。 > > 在涉及 r-s 對變量的記憶系統中，作者提出了以下術語和解釋：變量 R(可提取性)確定在給定時刻可以調用給定記憶軌跡的概率，而變量 S(記憶的穩定性)確定由于遺忘而導致的可提取性下降的速率，從而確定最佳重復間隔中的重復間隔的長度。 > > 假設可提取性以負指數下降，并將穩定性解釋為可提取性衰減常數的倒數，我們可以方便地使用以下公式(t 表示時間)來表示 R 和 S 之間的關系： > > - (3) `$ R=e^{-t/S} $` > > 從推理的步驟 1-5 中使用的 r-s 對到建議的解釋 R-S 的變換函數如下(假設最佳重復間隔的定義為產生知識保持的間隔 K=0.95)： > > - (4) `$ S=-s/\ln(K) $` > - (5) `$ R=e^{-(s-r)/S} $` > > 因此，第 i 次重復后的穩定性(`$ S_i $`)與確定由公式(1)和(2)定義的最佳重復間隔的常數 `$ C_1 $` 和 `$ C_2 $` 之間的關系可以寫成： > > - (6) `$ S_i=-(C_1*C_2^{i-1})/\ln(K) $` > > 最后，在最佳重復間隔中的可提取性可以表示為： > > - (7) `$ R_i(t)=\exp^{(t*\ln(K)/(C_1*C_2^{i-1}))} $` > > - 這里： > - i - 問題的重復次數 > - t - 從第 i 次重復開始的時間 > - `$ R_i(t) $` - 自第 i 次重復以來經過時間 t 之后的最佳重復間隔的可提取性 > - `$ C_1 $` 和 `$ C_2 $` - 來自公式(1)和(2)的常量。 > - K-知識保留量等于 0.95(重要的 是要注意由公式(7)表示的關系。由于較短間隔產生的間距效應，保留率高于 0.95 的情況可能不成立) ## SuperMemo 中的記憶的兩個組成成分 SuperMemo 一直基于記憶的雙組分模型，該模型在過去 30 年中以越來越明顯的形式出現。公式(2) 中的常數 `$ C_2 $` 在 Murakowski 的上述證明中表示穩定性增加。2018 年，穩定性增加在 SuperMemo 中表示為矩陣 SInc[]。`$ C_2 $` 說明在學習中應該增加多少重復間隔，才能達到可接受的遺忘水平標準。實際上，`$ C_2 $` 不是常數。這取決于許多因素。其中，最重要的是： - 項目難度(D)(參見：復雜性)：記住的信息越難，`$ C_2 $` 越小(即必須更頻繁地復習困難的材料) - [記憶穩定性](https://supermemo.guru/wiki/Memory_stability) (S)：記憶越持久，`$ C_2 $` 值越小 - 回憶概率([可提取性](https://supermemo.guru/wiki/Retrievability))(R)：回憶的概率越低，`$ C_2 $` 值越高(即由于[間隔效應](https://supermemo.guru/wiki/Spacing_effect)，如果延遲查看項目，可以更好地記住它們) 由于這些多重依賴關系，`$ C_2 $` 的精確值不容易預測。SuperMemo 通過使用多維矩陣來表示多自變量函數，并根據在實際學習過程中所做的測量來調整這些矩陣的值，從而解決了這個和類似的優化問題。這些矩陣的初始值是從理論模型或從先前的測量中導出的。隨著時間的推移，實際使用的值將與理論預測的值或根據以前學生的數據得出的值略有不同。 例如，如果給定難度、給定記憶狀態的給定項的 `$ C_2 $` 值產生的重復間隔比期望的間隔長(即產生的回憶率低于期望的水平)，則 `$ C_2 $` 值相應減少。 以下是[穩定性增加](https://supermemo.guru/wiki/Stability_increase )(常數 `$ C_2 $`)多年來的演變： - 在紙筆版本的 SuperMemo(1985) 中，`$ C_2 $` 確實(幾乎)是一個常數。設置為平均 1.75 (為了舍入誤差和簡單性，從 1.5 到 2.0 不等)，沒有考慮材料難度、穩定性或記憶的可提取性等。 - 在 [SuperMemo for DOS](https://supermemo.guru/wiki/SuperMemo_for_DOS)(1987) 的早期版本中，`$ C_2 $` (命名為 E-因子)首次反映了項目難度。成績不好時降低，成績好時增加。 - SuperMemo 4(1989) 沒有使用 `$ C_2 $`，但是為了計算重復間隔，它第一次使用了優化矩陣 - 在 [SuperMemo 5](https://supermemo.guru/wiki/SuperMemo_5) (1990) 中，`$ C_2 $` (命名為 O-因子)最終被表示為一個矩陣，它既包括難度維度，也包括穩定性維度。同樣，矩陣的條目將受到測量-驗證-校正循環的影響，該循環將從基于先前測量的初始值開始，產生向滿足學習標準的值的收斂 - 在 [SuperMemo 6](https://supermemo.guru/wiki/SuperMemo_6)(1991) 中，`$ C_2 $` 以 [O-因子矩陣](https://supermemo.guru/wiki/O-Factor_matrix)的形式派生自一個包含可提取性維度的三維矩陣。第三維度的重要意義是，[SuperMemo](https://supermemo.guru/wiki/SuperMemo) 第一次使檢查不同難度和記憶穩定性的遺忘曲線成為可能 - 在 [SuperMemo 8](https://supermemo.guru/wiki/SuperMemo_8)(1997) 到 [SuperMemo 16](http://www.super-memo.com/supermemo16.html) 中，`$ C_2 $` 的表示沒有有太大變化，但是，用于產生從理論數據到真實數據的快速而穩定的轉換的算法將逐漸變得越來越復雜。最重要的是，新的 SuperMemo 更好地利用了 `$ C_2 $` 的可提取性性維度。因此，與間隔效應無關，學生可以偏離初始學習標準，例如在考試前臨時抱佛腳，而不會在優化過程中引入噪聲 - 在 [SuperMemo 17](https://supermemo.guru/wiki/SuperMemo_17) (2016) 中，`$ C_2 $` 最終采取了基于最初的記憶雙組分模型的形式。它取自穩定性增加矩陣(SInc)，該矩陣具有三個維度，表示決定穩定性增加的三個變量：復雜性、穩定性和可提取性。在使用稱為算法 SM-17 的復雜算法學習期間用數據填充 SInc 矩陣。可使用 **Tools：Memory：4D Graphs** (**穩定性** 選項卡)在 SuperMemo 17 中檢查穩定性增加矩陣。