# 1989: SuperMemo 適應用戶記憶 [TOC=2,5] ## 引入彈性間隔函數 [SuperMemo 2](https://supermemo.guru/wiki/SuperMemo_2) 很棒。它的簡單算法已經在流行的應用程序（如[Anki](https://supermemo.guru/wiki/Anki)或[Mnemosyne](https://supermemo.guru/wiki/Mnemosyne)）中[存活至今](https://supermemo.guru/wiki/exponential_growth_of_the_popular)。然而，該算法是愚蠢的，因為其沒有辦法修改[最優間隔](https://supermemo.guru/wiki/Optimum_interval)的函數。[1985](https://supermemo.guru/wiki/Birthday_of_SuperMemo) 的發現是板上釘釘的。記憶[復雜度](https://supermemo.guru/wiki/Complexity)和[穩定性增加](https://supermemo.guru/wiki/Stability_increase)用相同的數字表示：[E-factor](https://supermemo.guru/wiki/E-factor)。這有點像在自行車上使用同一個控制桿來改變檔位和方向。 單個的[項目](https://supermemo.guru/wiki/Item)可以根據其估計的[難度](https://supermemo.guru/wiki/Complexity)來調整復習的間隔。這些變化可以補償[最優間隔](https://supermemo.guru/wiki/Optimum_interval)函數中的錯誤。即使算法收斂速度慢，理論上也是收斂的。主要的缺陷是，在[算法 SM-2](https://supermemo.guru/wiki/Algorithm_SM-2) 中，新項目不會從舊項目的經驗中受益。 [算法 SM-2](https://supermemo.guru/wiki/Algorithm_SM-2) 沒有適應能力。新[項目](https://supermemo.guru/wiki/Item)不受益于舊項目的經驗 算法 SM-4 是第一次嘗試用通用的適應性武裝 [SuperMemo](https://supermemo.guru/wiki/SuperMemo)。它于 1989 年 2 月竣工。最后，適應性表現得太慢了，但是用算法 SM-4 收集的靈感對于進一步發展是至關重要的，特別是在理解[間隔重復](https://supermemo.guru/wiki/Spaced_repetition)中的穩定性與準確性問題上。簡而言之，SM-4 算法太過穩定而不能準確。這在 7 個月后的 SM-5 算法中很快得到了糾正。以下是我的[碩士論文](https://supermemo.guru/wiki/Master's Thesis)的一段摘錄。 > 檔案警告:[為什么使用文字檔案?](https://supermemo.guru/wiki/Why_use_literal_archives%3F) > > 本文是 [Piotr Wozniak](https://supermemo.guru/wiki/Piotr_Wozniak) 的《*優化學習*》(1990)的一部分。 > > [算法 SM-2](https://supermemo.guru/wiki/Algorithm_SM-2) 的主要錯誤似乎是最優間隔函數的任意形狀。雖然在實踐中非常有效，并且經過多年的實驗重復得到了證實，但是**這個函數并不能被科學地證明其有效性**，也不能檢測出最優間隔的幾天變化對學習過程的整體影響。考慮到這些缺陷，我決定使用常規的 SuperMemo 重復來驗證最優間隔的作用! > > 使用那些在尋找[E因子](https://supermemo.guru/wiki/E-Factor)時應用的優化過程，我想讓程序在任何時候修正最初提出的函數，只要修正看起來是合理的。 > > 為了達到這個目的，我把最優間隔的函數列成表。 > > [](https://supermemo.guru/wiki/File:Matrix_of_optimum_intervals_in_SuperMemo_5.jpg) > > > **圖片：**最優間隔矩陣出現在1989年的SuperMemo 4中，并在SuperMemo 17中保留至今，幾乎沒有變化。在SuperMemo 4中，它是優化間距的信息來源。在SuperMemo 17中，它是由算法SM-15生成的矩陣得到的，同時與算法SM-17使用。這幅圖展示了一個來自SuperMemo 5的矩陣，并顯示了與原始矩陣值的顯著偏離。在SuperMemo 4中，改編的速度要慢得多 > > 最優間隔矩陣(后來稱為OI矩陣)的初始項最初取自算法SM-2中的公式。 > > SuperMemo 4(1989年2月)實現了新的解決方案，使用OI矩陣來確定重復間隔的值: > > > I(n):=OI(n,EF) > > > > 上式中： > > > > - I(n) - 給定項目的第n次重復間隔(以天為單位)， > > - EF - 項目的E-Factor， > > - OI(n,EF) - OI矩陣中對應第 n 次重復和 EF 的項目。 > > 然而，OI 矩陣并不是固定的。在重復的過程中，矩陣的具體項隨著分數的不同而增加或減少。例如，如果項目指出最優的間隔是 X，使用的間隔是 X+Y，而這個間隔之后的等級不低于 4，那么項目的新值將落在 X 和 X+Y 之間。 > > 因此，處于平衡狀態的 OI 項的值應該穩定在一個點上，在這個點上，低保留項流與高保留項流對矩陣的影響相平衡。 > > 因此，SuperMemo 4 試圖給出最優間隔函數的最終定義。 ## 剛性 SuperMemo 4 我很快就意識到新算法的驗證-校正周期太長了。這與在計算機上運行 [1985 年實驗](https://supermemo.guru/wiki/Birth_of_SuperMemo)沒有太大的不同。為了確定十年的間隔，我需要十年的時間來測試審查的結果。這導致了七個月后的 [算法 SM-5](https://supermemo.guru/wiki/Algorithm_SM-5)。以下是我在[碩士論文](https://supermemo.guru/wiki/Master's _thesis)中描述的算法 SM-4 的問題: > 檔案警告:[為什么使用文字檔案?](https://supermemo.guru/wiki/Why_use_literal_archives%3F) > > 本文是 [Piotr Wozniak](https://supermemo.guru/wiki/Piotr_Wozniak) 的《*優化學習*》(1990)的一部分。 > > 算法 SM-4 在 SuperMemo 4 中實現，并在 1989 年 3 月9 日至 1989 年 10 月 17 日期間使用。雖然修改最優間隔函數的主要概念似乎是向前邁出的一大步，但是算法的實現是失敗的。該算法的基本不足似乎源于在修改OI矩陣時應用的公式。 > > 有兩個最明顯的缺陷: > > - 修改太過細微，無法在合理的短時間內明顯地重新排列 OI 矩陣， > - 對于較長的間隔重復時間，修改的效果需要很長時間才能穩定固定，即需要很長時間才能看到幾個月間隔修改的結果，并在必要時進行修正 > > 在使用 SM-4 算法 7 個月后，特定數據庫的 OI 矩陣與它們的初始狀態并沒有太大的不同。人們可以用我早先關于最優重復間隔真值的預測的正確性來解釋這一事實，然而，正如后來用算法SM-5證明的那樣，矩陣穩定的實際原因是優化公式中的缺陷。 > > 就獲取率和保留率而言，沒有可靠的證據表明 SM-4 算法帶來了任何進展。輕微的改進也可能與軟件的總體改進和項目制定原則的改進有關。 ## SuperMemo4 的殘余在新的 SuperMemo 里 有趣的是，你仍然可以在新版本的 SuperMemo 中看到最優間隔矩陣。這個矩陣并沒有被算法使用，但是它顯示在SuperMemo 統計數據中，因為它告訴用戶[復雜性](https://supermemo.guru/wiki/Complexity)對學習過程中項目的前景的影響。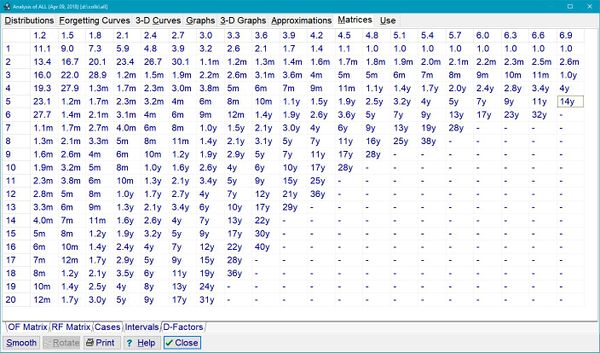 如果你比較一個使用了 8 個月的 [SuperMemo 5](https://supermemo.guru/wiki/SuperMemo_5) 生成的矩陣，你會發現它與使用了 20 年的[算法 SM-8](https://supermemo.guru/wiki/Algorithm_SM-8) 生成的矩陣有顯著的相似性： [](https://supermemo.guru/wiki/File:Matrix_of_optimum_intervals_in_SuperMemo_17.jpg) > **圖片：**算法 SM-17 不再使用最優間隔矩陣。但是，仍然可以通過算法 SM-15 的步驟來生成。這些列與以A因子表示的材料的簡易度相一致。這些行對應于以重復類別表示的記憶穩定性 ## 算法SM-4 以下是我在[碩士論文](https://supermemo.guru/wiki/Master's _thesis)中描述的算法SM-4的概要:： > 檔案警告:[為什么使用文字檔案?](https://supermemo.guru/wiki/Why_use_literal_archives%3F) > > 本文是 [Piotr Wozniak](https://supermemo.guru/wiki/Piotr_Wozniak)(1990) 的《*優化學習*》的一部分。 > > **算法SM-4在SuperMemo4.0中的應用** > > 4. ### 算法 > > 1. 將知識分解為最小的卡片 > 2. 所有卡片的 EF 設置為 2.5 > 3. 列出以重復次數和 EF 為索引的 OI 矩陣 > 4. 使用下面的重復間隔來初始化 OI 矩陣： > - OI(1,EF)=1 > - OI(2,EF)=6 > - for n>2 OI(n,EF)=OI(n-1,EF)*EF > - OI(n,EF) - 難度為 EF 的卡片在第 n 次復習時的最優間隔 > 5. 使用 OI 矩陣來確定重復間隔： > - I(n, EF) = OI(n, EF) > - I(n, EF) - 難度為 EF 的卡片在第 n 次復習時的間隔 > - OI(n, EF) - OI 矩陣對應 n 和 EF 的值 > 6. 每次重復后都用 0-5 的成績來給回憶質量打分 > 7. 每次重復后都根據下列公式修改 EF： > - $EF'=EF+(0.1-(5-q)\times(0.08+(5-q)\times0.02))$ > - EF' - EF 的新值 > - EF - EF 的舊值 > - q - 回憶質量打分 > - 如果 EF < 1.3 則令 EF = 1.3 > 8. 每次重復后都修改 OI 矩陣上的相關項 > 9. 一個示例公式如下（SM-4 中實際使用的公式更復雜）： > - $OI'=interval+\cfrac{interval\times (1-\cfrac{1}{EF})}{2}\times(0.25\times q-1)$ > - $OI''=(1-fraction)\times OI+fraction\times OI'$ > - OI - OI 對應項的舊值 > - OI' - 計算 OI 對應項新值的輔助值 > - OI'' - OI 對應項的新值 > - interval - 之前的間隔 > - fraction - 調和參數 > - EF - 重復卡片的 EF > - q - 回憶質量評分 > - 注意，當 q = 4 時 OI 不會改變，當 q = 5 時 OI 增長是 q = 0 時減少的 4 分之一 > 10. 如果回憶質量小于 3，卡片重新開始復習，并且不改變其 EF > 11. 在某一天的每次重復練習之后，再重復那些在回憶質量評分中得分低于4分的卡片。繼續重復，直到所有這些卡片得分至少4分。 ## 間隔矩陣的問題 SM-4 表明，除了收斂速度慢以外，使用間隔矩陣會導致一些問題，而用 OF 來替換間隔可以很容易解決。這些額外的缺陷使 SM-5 快速實現。以下是使用最優間隔矩陣的缺陷： > 檔案警告:[為什么使用文字檔案?](https://supermemo.guru/wiki/Why_use_literal_archives%3F) > > 本文是[Piotr Wozniak](https://supermemo.guru/wiki/Piotr_Wozniak)(1990)的《*優化學習*》的一部分。 > > - 在重復過程中，可能會發生一個間隔在計算后短與前一個間隔的情況，這與 SuperMemo 的假設不一致。此外，即使可以通過不允許間隔增加或減少超過某值來避免這種情況，但這會極大減慢矩陣的優化過程。 > - 特定卡片的 EF 會不斷修改，因此在 OI 矩陣中，一個卡片可以從一個難度類別轉移到另一個難度類別。如果卡片重復的次數足夠大，將會導致卡片重復過程的嚴重影響。注意，卡片連續重復次數越大，相鄰的 EF 列的最優間隔間的差異就越大。如果 EF 增加，卡片的最優間隔會變得不自然的長，在相反的情況下間隔可能會變得太短。 > > SM-4 嘗試將最優間隔的長度和重復次數相關聯。這種方法似乎是不正確的。因為記憶對之前使用的重復間隔長度更敏感，而不是重復次數。 ## SuperMemo 5 最優間隔矩陣的概念誕生于 1989 年 2 月 11 日。[SuperMemo](https://supermemo.guru/wiki/SuperMemo)將為不同水平的記憶穩定性和難度保存一組最優間隔。它將根據新數據流修改間隔。1989 年 3 月 1 日，我開始使用 SuperMemo 4 來學習世界語。我很早就注意到這個想法需要全面修改。算法的收斂速度慢得要命。 1989 年 5 月 5 日，我有了一個新想法。從本質上講，這就是[穩定性增長](https://supermemo.guru/wiki/Stability_increase)函數的誕生，除了在 [SuperMemo](https://supermemo.guru/wiki/SuperMemo) 的最優復習中沒有[可提取性](https://supermemo.guru/wiki/Retrievability)維度。新算法將使用[最優因子矩陣](https://supermemo.guru/wiki/Matrix_of_optimum_factors)。它不會記住最優的時間間隔，而是記住需要根據[記憶復雜度](https://supermemo.guru/wiki/memory_復雜性)和當前[記憶穩定性](https://supermemo.guru/wiki/Memory_stability)增加多少時間間隔。算法 SM-4 的緩慢收斂也激發了[隨機化間隔](https://supermemo.guru/wiki/History_of_spaced_repetition_(print)#randomization)的需求(1989年5月20日)。 與此同時，SuperMemo](https://supermemo.guru/wiki/SuperMemo) 的進展又一次因為學校的義務而被推遲。在 [Krzysztof Biedalak](https://supermemo.guru/wiki/Krzysztof_Biedalak) 的幫助下，我們決定編寫一個程序，用于開發可以與 SuperMemo 一起使用的學校測試。這個項目再次被用來在開明的 Krzysztof 博士的課堂上擺脫其他義務，Krzysztof 現在已經成為 SuperMemo 的支持者。 我花了一個夏天在荷蘭進行實踐訓練，由于各種義務(包括**強制**遠足！)進展緩慢。速度慢的主要原因之一是極端節食，這是因為需要存錢來償還我的PC1512債務。我還希望能多掙些錢給我的電腦買個硬盤。多虧了埃因霍溫大學的Peter Klijn的幫助，我的所有工作才得以完成。他只是把他的電腦給了我，讓我在整整兩個月的時間里私人使用。他不想讓我在SuperMemo上出色的工作慢下來。這是我第一次可以把所有的文件都保存在硬盤上，感覺就像是從一輛舊自行車搬到了特斯拉S型車。 直到 1989 年 10 月 16 日，新的算法 SM-5 才完成，我開始使用 SuperMemo 5。我在筆記中寫道：“*一場偉大的革命即將到來*”。確實取得了巨大的進展。 我有幾個 SuperMemo 2 的用戶準備升級到 SuperMemo 5。我只要求一個條件：他們將從初始化為特定值的最優因子矩陣開始。這是為了驗證算法，并確保它沒有先入為主的偏見。所有預先設定的優化矩陣將很好地快速收斂。這一事實隨后被用來主張普遍收斂，該算法在[關于間隔重復算法的第一本出版物](https://supermemo.guru/wiki/Optimization_of_repetition_spacing_in_the_practice_of_learning)中被這樣描述。不要讀那份出版物！它已經被[同行評審](https://supermemo.guru/wiki/Peer_review)閹割了。閱讀下面的內容來理解 SM-5 算法。 ## 算法SM-5 [SuperMemo](https://supermemo.guru/wiki/SuperMemo) 使用了一個簡單的原則：*“使用、驗證和糾正”*。在[重復](https://supermemo.guru/wiki/Repetition)之后，在[OF 矩陣](https://supermemo.guru/wiki/OF_matrix)的幫助下計算一個新的間隔。計算時間間隔的“相關項目”取決于重復(類別)和項目難度。在[間隔時間](https://supermemo.guru/wiki/Interval)過后， SuperMemo 要求下一次重復。使用[成績](https://supermemo.guru/wiki/Grade)來告訴 SuperMemo 這個間隔“表現”得如何。如果成績較低，我們有理由相信，間隔太長，[OF 矩陣](https://supermemo.guru/wiki/OF_matrix) 對應的項太大。在這種情況下，我們稍微減少了對應的項。這里的相關項目是之前用于計算間隔(即在間隔開始之前)的項目。換句話說，項目(1)用于計算間隔(n次重復之后)，然后(2)用于糾正[OF 矩陣](https://supermemo.guru/wiki/OF_matrix) (n+1次重復之后)。 以下是我的[碩士論文](https://supermemo.guru/wiki/Master's _thesis)中給出的算法SM-5的概要: > 檔案警告:[為什么使用文字檔案?](https://supermemo.guru/wiki/Why_use_literal_archives%3F) > > 本文是[Piotr Wozniak](https://supermemo.guru/wiki/Piotr_Wozniak)(1990)的《*優化學習*》的一部分。 **SuperMemo 5算法的最終公式如下(算法SM-5):** 1. 將知識分成盡可能小的項目 2. 所有項目的 [E-Factor](https://supermemo.guru/wiki/E-Factor) 等于 2.5 3. 將不同重復次數和 EF 類別的矩陣制表。使用以下公式： 1. OF(1,EF):=4 2. for n>1 OF(n,EF):=EF 3. 其中： 1. OF(n,EF) - 對應給定簡易度和連續復習次數 n 的最優因子 4. 使用 OF 矩陣確定重復間隔： 1. I(n,EF)=OF(n,EF)*I(n-1,EF) 2. I(1,EF)=OF(1,EF) 3. 其中： 1. I(n,EF) - 給定 EF 值的卡片的連續第 n 個間隔 2. OF(n,EF) - OF 矩陣對應給定簡易度和連續復習次數 n 的 OF 值 5. 在每次重復之后，在 0-5 級量表中評估[成績](https://supermemo.guru/wiki/Grade) (cf.算法SM-2) 6. 每次重復后，根據公式修改最近重復項的e因子： 1. EF':=EF+(0.1-(5-q)\*(0.08+(5-q)\*0.02)) 2. 其中： 1. EF' - 簡易度的新值 2. EF - 簡易度的舊值 3. q - [quality of the response](https://supermemo.guru/wiki/Grade) in the 0-5 grade scale 3. 如果 EF 小于 1.3，則將 EF 設置為 1.3 7. 每次重復后修改矩陣的相關項目。任意構造并在修改中使用的示例性公式可以是這樣的： 1. OF':=OF*(0.72+q*0.07) 2. OF*:=(1-fraction)\*OF+fraction\*OF'* 3. 其中： 1. OF *- OF 的新值 2. OF' - 計算 OF 新值的輔助值 3. OF - OF 的舊值 4. fraction - 0~1之間的一個值，越大 OF 改變越大 5. q - [回憶質量打分](https://supermemo.guru/wiki/Grade) 0 - 5 4. 請注意，對于 q=4 ，OF 不變。q>4 時增大，q<4 時減小。 8. 如果 q 小于 3，則不改變 EF 的值，項目從頭開始復習。 9. 在某一天的每一次重復之后，重復所有在[回憶質量打分](https://supermemo.guru/wiki/Grade)中得分低于 4 分的項目。繼續[重復](https://supermemo.guru/wiki/Repetition)，直到所有這些[項目](https://supermemo.guru/wiki/Item)得分至少 4 分 根據之前的觀察，[OF 矩陣](https://supermemo.guru/wiki/OF_matrix)的項不允許低于 1.2。在算法 SM-5 中，根據定義，[間隔](https://supermemo.guru/wiki/Interval)不能在連續的[重復](https://supermemo.guru/wiki/Repetition)中變得更短。時間間隔至少是其前身的 1.2 倍。更改 [E-Factor](https://supermemo.guru/wiki/E-Factor) 類別僅增加下一個應用的間隔，增加的倍數與 [OF 矩陣](https://supermemo.guru/wiki/OF_matrix)相應項所需的倍數相同。 ## 對 SM-5 算法的批評 [Anki](https://supermemo.guru/wiki/Anki) 手冊中包含了一段對 SM-5 算法出乎意料的批評(2018 年 4 月)。這些話特別令人驚訝，因為算法 SM-5 從來沒有完整地發表過(上面的版本只是一個粗略的大綱)。盡管批評的話語顯然是善意的，但它們暗示了一種可能性，即如果[算法 SM-2](https://supermemo.guru/wiki/Algorithm_SM-2)是優于[算法 SM-5](https://supermemo.guru/wiki/Algorithm_SM-5)，或許它也優于[算法 SM-17](https://supermemo.guru/wiki/Algorithm_SM-17)。如果是這樣的話，我就浪費了過去 30 年的研究和編程。時至今日，維基百科還在“批評” “[SM3+](https://supermemo.guru/wiki/SM3%2B)”。“SM3+” 是最初在[Anki](https://supermemo.guru/wiki/Anki)手冊中使用的一個標簽，已經在網絡上的幾十個站點使用(特別是那些因其簡單性而傾向于堅持使用較舊算法的人)。[這里](https://supermemo.guru/wiki/Universal_metric_for_cross-comparison_of_spaced_repetition_algorithms)比較了算法 SM-2 和算法 SM-17 。希望這不會有任何疑問。 ### Anki 手冊中的錯誤聲明 我的[碩士論文](https://supermemo.guru/wiki/Master's _thesis)于 1998 年在 [supermemo.com](https://supermemo.com/) 上摘錄發表，其中只包括對算法 SM-5 的粗略描述。為了清楚起見，數十個次要程序沒有公布。這些程序需要進行大量修改，以確保良好的收斂性、穩定性和準確性。這種修修補補需要幾個月的學習和分析相結合。算法 SM-5 從來沒有現成的開箱即用版本。 算法SM-5的源代碼從未發表或公開過，最初的算法只能在 MS DOS 下由 Supermemo 5 的用戶進行測試。SuperMemo 5 在 1993 年成為免費軟件。需要注意的是，圍繞最優值的隨機分散間隔是建立收斂性的關鍵。如果沒有[分散](https://supermemo.guru/wiki/History_of_spaced_repetition_(print)# random_dispersal_of_interval)，算法的進展將會慢得令人痛苦。同樣，[矩陣平滑](https://supermemo.guru/wiki/History_of_spaced_repetition_(print)# Matrix_smoothing)對于一致的行為是必要的，獨立于為不同級別的[穩定性](https://supermemo.guru/wiki/Stability)和項目[復雜性](https://supermemo.guru/wiki/Complexity)收集的數據的稀缺性。 在 1989 年和之后進行的多次評估表明，在任何研究的度量中，算法 SM-5 和之后的算法毫無疑問地優于[算法 SM-2](https://supermemo.guru/wiki/Algorithm_SM-2)。算法 SM-17 實際上可以用來衡量算法 SM-5 的效率，如果我們有志愿者用我們的[通用度量](https://supermemo.guru/wiki/Algorithm_SM-17)重新實現古老的代碼。到目前為止，我們已經對 SM-2 算法進行了比較。實現的成本微不足道。不用說，SM-2 算法在預測能力方面遠遠落后，特別是在[可提取性](https://supermemo.guru/wiki/Retrievability)的次優水平(在用戶沒有嚴格遵守規定時間表的情況下)。 即使對底層模型有基本的了解，也應該清楚一個好的實現將產生巨大的好處。SuperMemo 5 將根據用戶的記憶來調整它的間隔函數。SuperMemo 2 是固定不變的。我非常自豪的是，1985年和1987年的大膽猜測經受住了時間的考驗，但任何算法都不應該相信一個擁有 2 年間隔重復算法實現經驗的卑微學生的判斷。相反，Supermemo 4 和所有后續實現進行的猜測越來越少，并且提供了更好、更快的適應性。在所有這些實現中，只有 Supermemo 4 適應速度慢，并在 7 個月內被更好的解決方案取代。 Anki 的批評沒有惡意，但如果作者推動實施并迅速轉向自學，而不是花時間修補那些似乎不像他預期的那樣有效的程序，我不會感到驚訝。相比之下，在1989年，我知道算法SM-2是有缺陷的，我知道算法SM-5是更好的，我將不遺余力地確保新概念被完善到其最大的理論潛力。 Anki手冊摘錄(2018年4月): > Anki最初是基于 SuperMemo 的 SM5 算法。然而，Anki 在回答卡片之前顯示下一個間隔的默認行為揭示了 SM5 算法的一些基本問題。SM2 于后來修改的算法之間的關鍵區別是： > > - SM2 根據您的一張卡片上的表現來安排該卡片下一次的時間 > - SM3+ 根據您的一張卡片上的表現來安排該卡片，以及類似卡片下一次的時間 > > 后一種方法不僅考慮了單個卡片的表現，還考慮了作為一個組的表現，從而保證了選擇更準確的間隔時間。如果你在學習上非常一致，并且所有的牌都有一個非常相似的難度，這種方法可以很好地工作。然而，一旦在公式中引入了不一致性(不同難度的卡片，不是每天在同一時間學習)，SM3+ 更容易在下一個間隔中出現不正確的猜測——導致牌被安排得太頻繁或太遙遠。 > > 此外，當SM3+動態調整“最優因子”表時，經常會出現這樣的情況：在一張卡片上回答“困難”比回答“容易”的間隔時間更長。下一次時間在 SuperMemo 中是隱藏的，所以用戶永遠不會知道這個。 > > 在對備選方案進行評估之后，Anki 的作者認為，通過模仿 SM2 產生的接近最優間隔要比冒著錯誤猜測的風險獲得最優間隔更好。SM2 方法對用戶來說是可預測的和直觀的，而 SM3+ 方法對用戶隱藏了細節，并要求用戶信任系統(即使系統可能在調度中出錯) 在所有這些說法中，只有一個是正確的。[SuperMemo 2](https://supermemo.guru/wiki/SuperMemo_2)確實更直觀。多年來，這個問題一直困擾著 SuperMemo。每個版本都更復雜，很難向用戶隱藏其中的某些復雜性。我們將繼續努力。 這就是為什么 Anki 批評是不合理的原因： - 事實上，SuperMemo 5 利用所有項目的過去表現來最大化新項目的表現，這是一個優勢，而不是一個“問題”。更重要的是，這是適應性的關鍵 - 不一致的評分一直是所有算法的一個問題。平均而言，適應性有助于發現錯誤評分的平均影響，特別是如果不一致本身是一致的(即用戶在相似的情況下不斷犯類似的錯誤) - 混合的困難被 SuperMemo 5 處理得更好。在 SuperMemo 2 中難度和穩定性增長都是用 EF 編碼的，而在 SuperMemo 5 及以后的版本中，這兩種記憶特性是分開的 - 間隔預測在 SuperMemo 5 中被證明更優越，而“更容易出錯”的說法只能用實現中的錯誤來解釋 - 如果沒有實現矩陣平滑，較低的評分可能帶來更長的間隔。這部分算法在我的論文中只做了口頭描述 - 即使在更簡單的實現中(例如，對于手持設備、智能手機等)，間隔和重復日期也總是顯著地顯示在 SuperMemo 中。沒有向用戶隱藏任何東西。最重要的是，遺忘指數和工作量的統計數據是完全可見的，并且有可能看到 SuperMemo 是否履行了它承諾的保留，以及在怎樣的工作量代價下。 - 算法及其所有細節在 SuperMemo 5 中得到了充分的展示。特別是，在每次重復時將顯示對矩陣的更改。對于任何對算法有基本了解的人來說，它的操作都是完全透明的。全面的跟蹤也可以在 Anki 或其他應用程序中實現，但可能需要大量的修改。這將是昂貴的。最后，Anki 的選擇可能確實很好，因為它很簡單(從實現、操作、跟蹤、調試、維護、用戶直覺等方面來說)。 - “隱藏細節”的抱怨與神經網絡在間隔重復方面更優越的主張是截然相反的。與神經網絡實現不同，算法SM-5的操作比較容易分析 我們 2011 年在 [supermemopedia.com](http://supermemopedia.com/) 上發表的官方回應今天看來相當準確: > 檔案警告:[為什么使用文字檔案?](https://supermemo.guru/wiki/Why_use_literal_archives%3F) 很棒的是，Anki 介紹了自己的創新，同時仍然給予 SuperMemo 應有的贊譽。的確，與萊特納系統或紙面上的 Supermemo 相比，SuperMemo 的算法 SM-2 工作得很好。然而，SM-5 算法相對于 SM-2 算法的優越性是毋庸置疑的。無論是在實踐中還是在理論上都是如此。算法 SM-2 的時間間隔是固定的，并且只依賴于項目的難度，該難度可以用一個啟發式公式來近似(即一個基于 1987 年前有限經驗得出的猜測的公式)。確實，您不能通過向算法 SM-2 提供錯誤數據來“破壞”它。之所以如此，只是因為它不具有適應性。您可能更喜歡使用可自定義字體的文字處理程序，盡管您可能會通過應用修飾把文本弄亂。 SM-2算法簡單地用一個所謂的 [E-Factor](https://supermemo.guru/wiki/E-Factor) 來粗略地乘以間隔，這是一種表示項目[難度](https://supermemo.guru/wiki/難度)的方法。相反，算法 SM-5 收集用戶的表現數據，并相應地修改最優間隔的函數。換句話說，它適應學生的表現。算法 SM-6 甚至更進一步，修改了最優間隔的函數，以達到期望的[知識保留](https://supermemo.guru/wiki/Knowledge_retention)水平。這些新算法的優越性已經通過多種方式得到了驗證，例如，通過測量固定大小數據庫中工作負載隨時間的下降情況。在研究的案例中(小樣本)，與使用算法 SM-2 處理的舊數據庫(相同類型的材料：英語詞匯)相比，使用新算法處理的工作量下降速度幾乎是后者的兩倍。 所有的 SuperMemo 算法都將項目分成難度類別。算法 SM-2 給每個類別一個嚴格的間隔集。算法 SM-5 也給了每個類別一組間隔，但是這些間隔是根據用戶的表現來調整的，也就是說不是固定不變的。 “糟糕的評分”在算法 SM-5 中確實比在算法 SM-2 中更嚴重，因為錯誤的數據會導致“錯誤的適應”。然而，在 SuperMemo 中給出不真實/作弊的分數總是不好的，無論你使用哪種算法。 在有關記憶的知識不完整的情況下，適應性總是優于僵化的模型。這就是為什么適應一個不精確的平均值(如算法SM-5)要比根據一個不精確的猜測(如算法 SM-2)來確定間隔要好。 毋庸置疑，最后一個詞進入算法 SM-8 之后又變了，因為它適應了測得的平均值 ### SuperMemo5 的評估（1989） SuperMemo 5的優勢如此明顯，以至于我沒有收集太多數據來證明我的觀點。我只拿我的[碩士論文](https://supermemo.guru/wiki/Master's_thesis)做了幾次比較，結果毫無疑問。 檔案警告:[為什么使用文字檔案?](https://supermemo.guru/wiki/Why_use_literal_archives%3F) 本文是[Piotr Wozniak](https://supermemo.guru/wiki/Piotr_Wozniak)(1990)的《*優化學習*》的一部分。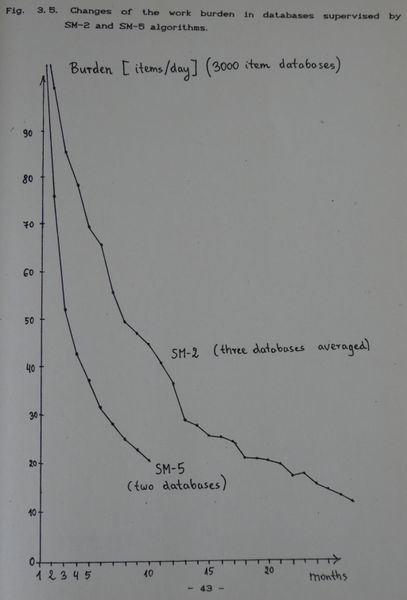 **3.8.算法 SM-5 的評估** 算法 SM-5 自 1989 年 10 月 17 日開始使用，它提供了一種確定理想的最優間隔函數的有效方法，超出了所有人的預期，從而提高了習得率(在 9 個月內學習了 15,000 個項目)。圖 3.5 顯示習得速率至少是組合應用 SM-2 和 SM-4 算法的兩倍！ [](https://supermemo.guru/wiki/File:Burdern_SM2_vs_SM5.jpg) > **圖片：**在 SM-2 和 SM-5 算法的監督下，數據庫中工作負擔的變化 對于 10 個月的數據庫，知識保留率提高到 96% 左右。下面列出了選定數據庫中的一些知識保留率數據，以顯示 SM-2 和 SM-5 算法之間的比較： - 日期 - 測量日期， - 數據庫 - 數據庫的名稱；ALL 表示所有數據庫的平均值 - 間隔 - 數據庫中項目使用的平均當前間隔 - 保留率 - 數據庫中的知識保留率 - 版本 - 數據庫所應用的算法版本 | Date | Database | Interval | Retention | Version | | :----: | :------: | :------: | :-------: | :-----------------: | | Dec 88 | EVD | 17 days | 81% | SM-2 | | Dec 89 | EVG | 19 days | 82% | SM-5 | | Dec 88 | EVC | 41 days | 95% | SM-2 | | Dec 89 | EVF | 47 days | 95% | SM-5 | | Dec 88 | all | 86 days | 89% | SM-2 | | Dec 89 | all | 190 days | 92% | SM-2, SM-4 and SM-5 | 在復習過程中，記錄了下列成績分布情況: | Quality | Fraction | | :-----: | :------: | | 0 | 0% | | 1 | 0% | | 2 | 11% | | 3 | 18% | | 4 | 26% | | 5 | 45% | 根據算法 SM-5 的假設，該分布產生的平均回憶質量等于 4。遺忘指數等于 11%(成績低于 3 的項目被認為是被遺忘的)。請注意，保留率數據表明數據庫中只有 4% 的項目沒有被記住。因此，遺忘指數超過遺忘項目百分比的 2.7 倍。 在一個 7 個月前的數據庫中，發現 70% 的項目在測量之前的重復過程中甚至沒有忘記一次，而只有 2% 的項目遺忘次數超過 3 次 ### 新算法優越性的理論證明 Anki 對 SuperMemo 5 的批評需要根據現代的[間隔重復](https://supermemo.guru/wiki/Spaced_repetition)理論來做一個簡單的證明。我們可以表明，今天的記憶模型可以映射到兩種算法基礎上的模型：[算法 SM-2](https://supermemo.guru/wiki/Algorithm_SM-2) 和[算法 SM-5](https://supermemo.guru/wiki/Algorithm_SM-5)，兩者之間的關鍵區別是最優間隔函數的適應性缺失(在算法SM-5中由最優因子矩陣表示)。 SInc = f (C、S、R) 是一個[穩定性增長](https://supermemo.guru/wiki/Stability_increase)函數，[復雜性](https://supermemo.guru/wiki/Complexity) C、[穩定](https://supermemo.guru/wiki/Stability) S、[可恢復性](https://supermemo.guru/wiki/Retrievability) R 作為參數。這個函數決定了最優學習中復習[間隔](https://supermemo.guru/wiki/Interval)的遞增。 兩種算法，SM-2 和 SM-5 都忽略了[可提取性](https://supermemo.guru/wiki/Retrievability)維度。理論上，如果兩種算法都能完美運行，我們可以假設它們的目標是 R=0.9。正如可以在 [SuperMemo](https://supermemo.guru/wiki/SuperMemo) 中測量的那樣，這兩種算法都失敗了，因為它們不知道相關的[遺忘曲線](https://supermemo.guru/wiki/Forgetting_curve)。他們只是不收集遺忘曲線數據。這種數據收集的可能性是在 1991 年才在[算法 SM-6](https://supermemo.guru/wiki/Algorithm_SM-6) 中引入的。 然而，如果我們假設 [1985](https://supermemo.guru/wiki/The_birthday_of_spaced_repetition:_July_31，_1985) 和 [1987](https://supermemo.guru/wiki/SuperMemo_1.0_for_DOS_(1987)) 啟發式是完美的猜測，在理論上，該算法可以使用SInc=F(C,S)，常數R為90%。 由于 SM-2 使用相同的數字 EF 用于穩定性增加和項目復雜性，對于 SM-2，我們有以 EF=f'(EF,interval) 的形式表示的 SInc=f(C,S) 方程，其中的數據可以很容易地顯示 f<>f' 。令人驚訝的是，SM-2 中使用的啟發式通過解耦 EF 和項目復雜性之間的實際聯系，使這個函數發揮作用。由于數據顯示 SInc 隨著 S 的增加而不斷減少，在算法 SM-2 中，根據定義，如果要用 EF 來表示項的復雜度，那么所有項都需要在每次復習時獲得復雜度。在實際應用中，算法 SM-2 使用 EF=f'(EF,interval)，即 SInc(n)=f(SInc(n-1),interval)。 讓我們假設 EF=f(EF,interval) 啟發式正如 SM-2 算法的支持者所聲稱的那樣，是一個很好的猜想。令 *SInc* 在算法 SM-5 中由 [O-factor](https://supermemo.guru/wiki/O-factor) 表示。然后我們可以將 *SInc*=f(C,S) 表示為 *OF*=f([EF](https://supermemo.guru/wiki/EF),[interval](https://supermemo.guru/wiki/Interval))。 對于算法 SM-2, OF 是常數，等于 EF，在算法 SM-5 中，OF是可適應的，可以根據算法的表現進行修改。很明顯，對表現差的算法進行懲罰，降低[OF 矩陣](https://supermemo.guru/wiki/OF_matrix)對應的項，并通過增加對應的項來獎勵它，這要優于保持不變。 有趣的是，盡管 SM-2 算法的支持者聲稱它表現得很好，但神經網絡 SuperMemo 算法的支持者卻不斷指責代數算法：缺乏適應性。實際上，[算法 SM-17](https://supermemo.guru/wiki/Algorithm_SM-17) 的適應性是最好的，因為它是基于最精確的[記憶模型](https://supermemo.guru/wiki/Three_component_model_of_memory)。 可以想象，在 SM-2 中使用的啟發法是如此精確，以致于原來對 *OF*=f(EF,interval) 的猜測不需要修改。然而，正如在實際應用中所顯示的那樣，[OF 矩陣](https://supermemo.guru/wiki/OF_matrix)迅速發展，并收斂到[這篇出版物(Wozniak, Gorzelanczyk 1994)](https://supermemo.guru/wiki/ANE1994)中描述的值。它們與算法 SM-2 中的假設有本質上的不同。 **總結：** - sm17 (2016): SInc=f(C,S,R)， 3 個變量，f 是有適應性的 - sm5 (1989): SInc=f(C,S,0.9)， 2 個變量，f 是有適應性的 - sm2 (1987): SInc=f(SInc,S,0.9) - 1 個變量，f 是固定的 ## 收斂 算法SM-5表現出了快速的收斂性，這很快被以單價[矩陣](https://supermemo.guru/wiki/OF_matrix)開始的用戶所證明。這與SM-4算法形成了鮮明的對比。 檔案警告:[為什么使用文字檔案?](https://supermemo.guru/wiki/Why_use_literal_archives%3F) 本文是[Piotr Wozniak]的《*優化學習*》(https://supermemo.guru/wiki/Piotr_Wozniak)(1990)的一部分。 **3.6.改進最優因子的預定矩陣** 在[矩陣](https://supermemo.guru/wiki/OF_matrix)的轉換中應用的優化過程似乎是令人滿意的有效的，從而使項目快速收斂到它們的最終值。 然而，在考慮的時期(1989年10月17日- 1990年5月23日)，只有那些以修改-驗證周期短(不到3-4個月)為特征的最優因素似乎達到了平衡值。 關于[矩陣](https://supermemo.guru/wiki/OF_matrix)的最終形狀，還需要幾年的時間才能得出更合理的結論。在分析了7個月大的矩陣后，最有趣的事實是，對于e因子等于2.5的矩陣，第一次重復間隔應該長達5天，對于e因子等于1.3的矩陣，甚至應該長達8天!第二個時間間隔對應的值分別為3周和2周左右。 新得到的[最優間隔]函數(https://supermemo.guru/wiki/Optimal_interval)表達式如下: > I(1)=8-(EF-1.3)/(2.5-1.3)*3 > > I(2)=13+(EF-1.3)/(2.5-1.3)*8 > > for i>2 I(i)=I(i-1)*(EF-0.1) > > 上式中： > > - I(I) -第I次重復后的間隔(以天為單位) > - EF - [E-Factor](https://supermemo.guru/wiki/E-Factor)。 為了加速優化過程，應該使用這個新函數來確定矩陣的初始狀態(SM-5算法的第3步)。除了第一個間隔外，這個新函數與SM-0到SM-5算法中使用的函數沒有顯著的區別。人們可以把這一事實歸因于優化過程的低效，畢竟，這是由應用預先確定的矩陣的事實所造成的。為了確保這不是事實，我讓我的三個同事使用SuperMemo 5.3的實驗版本，其中使用了一價矩陣(在兩個實驗中所有的項目都等于1.5，在剩下的實驗中等于2.0)。 雖然實驗數據庫的使用時間只有2-4個月，但矩陣的收斂速度似乎緩慢地趨近于使用預先確定的矩陣所得到的形式。然而，矩陣的預定繼承了E-Factor與相關E-Factor類元素值之間的人工相關性(即對于n>3， (n,EF)的值接近于EF)。這種現象在單葉矩陣中不存在，單葉矩陣傾向于根據算法中任意選擇的元素如e因子初值(始終為2.5)、函數重復后修改e因子等要求對矩陣進行更緊密的調整。 ## 矩陣平滑 一些[Anki的作者批評](https://supermemo.guru/wiki/History_of_spaced_repetition_(print)#Criticism_of_Algorithm_SM-5)可能是由于沒有采用矩陣平滑算法的一個重要組成部分,至今仍用于[算法SM-17](https://supermemo.guru/wiki/Algorithm_SM-17)。 檔案警告:[為什么使用文字檔案?](https://supermemo.guru/wiki/Why_use_literal_archives%3F) 本文是[Piotr Wozniak]的《*優化學習*》(https://supermemo.guru/wiki/Piotr_Wozniak)(1990)的一部分。 **3.7.變化在最優因子矩陣上的傳播** 注意到前面提到的矩陣中各元素之間關系的規律性，我決定通過在矩陣中傳播修改來加速優化過程。如果一個最優因子增加或減少，那么我們可以得出結論，與較高的重復次數相對應的因子也應該增加。 這是從(i,EF)= (i+1,EF)的關系得出的，它對所有[e - factor](https://supermemo.guru/wiki/E-Factor)和i>2大致有效。類似地，如果我們記得對于i>2，我們有of (i,EF')= of (i,EF*)\*EF'/EF*(特別是如果EF'和EF*足夠接近的話)，我們可以考慮理想的因子變化。我只在還沒有被重復反饋修改過的矩陣上使用變化的傳播。這證明了特別成功的情況下，一價矩陣適用于SuperMemo的實驗版本在前一段提到 所提出的傳播方案可以概括為: 1. 執行算法SM-5的第7步后，定位在重復過程中尚未被修改的of矩陣的所有相鄰的項，即未進入修改-驗證循環的項。相鄰項在這里理解為對應重復次數+/- 1和e因素類別+/- 1(即e因素+/- 0.1)的項。 2. 當下列關系之一不成立時，修改相鄰的項: - for i>2 (i,EF)=OF(i+1,EF) for all EFs - for i>2 OF(i,EF')=OF(i,EF*)\*EF'/EF* - 因為i=1 OF(i,EF')=OF(i,EF*)* 3. 對于第2步中修改的所有項目，重復查找它們尚未修改的鄰居的整個過程。 變化的傳播似乎是不可避免的，如果你記得最優間隔的函數取決于這樣的參數: - 學生的能力 - 學生的自我評價習慣(響應質量根據學生的主觀意見給出) - 記憶知識的性質等。 因此，不可能提供一個理想的、預先確定的矩陣，而不使用修改-驗證過程和(在較小程度上)傳播方案。 時間間隔的隨機散布 ## 間隔的隨機散布 算法SM-5的關鍵改進之一是間隔的隨機散布。一方面，它極大地加快了優化過程，另一方面，它給幾乎所有未來版本的SuperMemo的用戶造成了極大的困惑:*“為什么相同等級的相同項目每次使用不同的間隔時間?”*。微小的偏差是寶貴的。當“naked”[算法SM-17](https://supermemo.guru/wiki/Algorithm_SM-17)在早期的SuperMemo 17中發布時，這個問題就暴露出來了。可以看出，那些收藏了大量[水蛭](https://supermemo.guru/wiki/Leech)的用戶很容易就會遇到“局部極小值”，從此他們再也出不來了。隨機離散度在一定的延遲下恢復。“赤裸”這段時間對算法的準確觀察是需要的，尤其是在我這樣的幾十年的學習過程中。 檔案警告：為什么使用文獻存檔？ 這篇文章是[Piotr Wozniak]的一部分:“改進學習”(https://supermemo.guru/wiki/Piotr_Wozniak) (1990) **3.5.最優間隔的隨機散布** 為了進一步改進優化過程，引入了一種可能與最優重復間隔原則相矛盾的機制。讓我們重新考慮一下算法SM-5的一個重大錯誤:只有在滿足以下條件時，才能對一個最優因子的修改進行正確性驗證: - 修正因子用于計算重復間隔 - 計算的時間間隔過去了，重復的時間間隔產生的響應質量可能表明需要增加或減少最優因子 這意味著即使大量的實例用于修改一個最優因子，也不會顯著地改變它，直到新計算的值被用于確定新的間隔，并在它們過去后進行驗證。 在重復使用一段時間后對修改過的最優因素進行驗證的過程以后將稱為修改-驗證周期。重復次數越大，修改-驗證周期越長，優化過程的慢化程度越大。 為了說明修改約束的問題，讓我們考慮圖[3.4]中的計算(http://super-memory.com/english/ol/sm5.htm)。 我們可以很容易地得出結論，對于變量INTERVAL_USED大于20，如果質量等于5，那么MOD5的值將等于1.05。當質量=5時，修改器將等于MOD5，即1.05。因此，新提出的最優因子(NEW_OF)只能比前一個(NEW_OF:=USED_OF*MODIFIER)大5%。因此，修改后的最優因子永遠不會超過5%的極限，除非USED_OF增加，這相當于將修改后的最優因子應用于計算重復間隔。 考慮到這些事實，我決定在某些情況下讓重復間隔與最優間隔不同，以繞過修改-驗證周期的約束。 我把這個過程稱為最優間隔的隨機修正散布。 如果允許一小部分時間間隔更短或更長時間比它應該遵循從矩陣的這些不正常的間隔可以加速最優因素的變化,讓他們減少或增加超越極限的機制提出了圖(3.4)(http://super-memory.com/english/ol/sm5.htm)。換句話說，當一個最優因子的值與期望的值有很大的差異時，由于響應特性更傾向于促進變化，而不是與之相反，因此由偏差間隔引起的偶然變化不會被標準重復流拉平。 使用最優間隔的另一個好處是消除了SuperMemo用戶經常抱怨的一個問題——重復調度的混亂。我所說的重復計劃的塊塊性，是指重復工作在某天的積累，而相鄰的日子則相對沒有負擔。這是由于學生們在一次學習中往往記住了大量的項目，而這些項目往往在接下來的幾個月里粘在一起，僅根據他們的電子因素分開。 在最優間隔周圍散布間隔消除了塊狀問題。現在讓我們考慮一下最新的SuperMemo軟件在散布接近最優值的間隔時所使用的公式。與被認為是最優的間隔(根據矩陣的形式)稍有不同的重復間隔稱為接近最優的間隔。近似最優間隔按下式計算: > NOI=PI+(OI-PI)*(1+m) > > 上式中： > > - NOI-接近最優間隔 > - PI-使用以前的間隔 > - OI-由矩陣計算的最優間隔(cf.算法SM-5) > - m-屬于<-0.5、0.5>范圍的數字(見下文) > > 或使用 OF 值： > > NOI=PI*(1+(OF-1)*(1+m)) > > NOI=PI+(OI-PI)*(1+m) 修改器m將確定偏離最優間隔的程度(m =-0.5或m=0.5值的最大偏差，m=0時完全沒有偏差)。 為了在加速優化和消除塊度(兩者都需要很強的分散重復間隔)和高保留(嚴格應用最優間隔)之間找到一個折衷點，m在大多數情況下應該有一個接近于零的值。 利用以下公式確定修飾語m的分布函數: - -在<0,0.5>范圍內選擇一個修飾語的概率應該等于0.5: - 假設選擇一個修飾語m=0的概率是選擇m=0.5的概率的100倍: - 假設概率密度函數為負指數形式，參數a和b在前兩個方程的基礎上: 上述公式對于以百分比表示的m，則得a=0.04652, b=0.09210。 從分布函數 > 從-m到m的積分a*exp(-b*ab (x))dx = P (P表示概率) 我們可以得到修飾符m的值(對于m>=0): 因此，計算接近最優間隔的最終步驟如下: > a:=0.047; > > b:=0.092; > > p:=random-0.5; > > m:=-1/b*ln(1-b/a*abs(p)); > > m:=m*sgn(p); > > NOI:=PI*(1+(OF-1)*(100+m)/100); > > 其中: > > - random - 函數的取值范圍 <0,1)，具有均勻分布的概率 > - NOI - 接近最優間隔 > - PI - 以前使用的間隔 > - OF - 矩陣的相關項