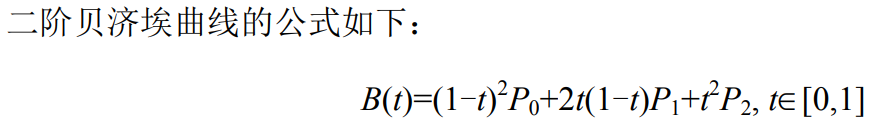
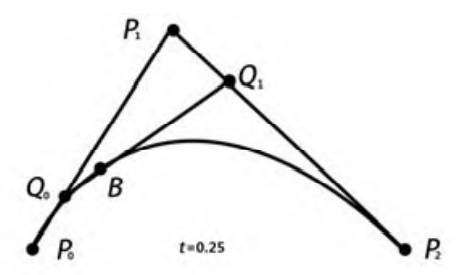
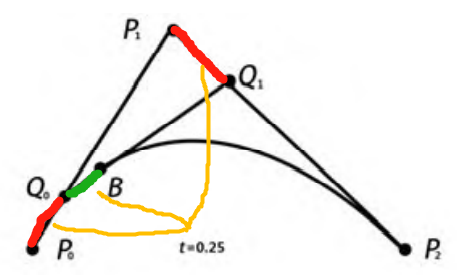
[TOC] # 1. 前言 貝塞爾曲線(Bézier curve)，又稱貝茲曲線或貝濟埃曲線，是應用于二維圖形應用程序的數學曲線。一般的矢量圖形軟件通過它來精確畫出曲線，貝茲曲線由線段與節點組成，節點是可拖動的支點，線段像可伸縮的皮筋，我們在繪圖工具上看到的鋼筆工具就是來做這種矢量曲線的。 # 2. 介紹 ## 2.1 一階貝濟埃曲線 一階貝濟埃曲線的公式如下： ``` B(t)=(1-t)P_0+tP_1，t屬于0-1 ``` P0為起始點，P1為終點，t 表示當前時間，B(t)表示公式的結果值。其實也就是一條從P0到P1的直線上，勻速運動的點值。 ## 2.2 二階貝塞爾曲線    這條曲線的構成也就是每個t時刻，Q0和Q1的所屬的直線的的t時刻的距離的點，這里也就是B。不妨將上面這個圖簡單標注下：  也就是在從P0到P1，進行勻速運動，在t=0.25的時刻走到Q0，類似的，從P1到P2經過勻速運動，在t=0.25的時刻走到Q1，對于Q0到Q1，經過勻速運動，在t=0.25的時刻走到B。而B也就是二階貝塞爾曲線上的點。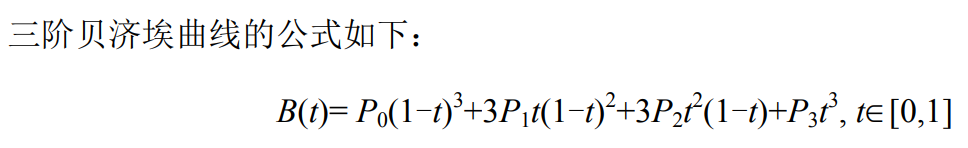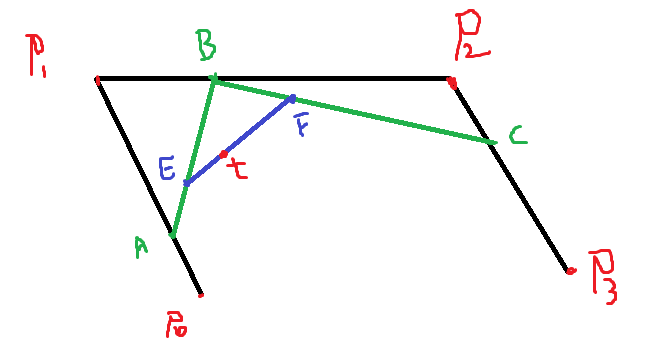 ## 2.3 三階貝塞爾曲線  也就是說此時有兩個控制點，對應著也就是三根連著的線段，類似的我們可以得到最終的t點：  那么，根據上面的規則，我們可以自己來實現一下貝賽爾曲線的計算方式，并將曲線繪制出來。 # 3. 一、二、三階貝塞爾曲線實現 定義為： ~~~ class Point(var x: Float, var y: Float){ } /** * 得到貝賽爾曲線上的點集 * @param points 起始、控制和終止點坐標 * @param number 需要計算的貝賽爾曲線上的點的個數 * @return 返回路徑 */ private fun getBezierPointsPath(points: Array<Point>, number: Int): Path{ val path = Path() for (time in 0 until number){ val t = time * 1f / number val point = calcPoint(points, t) if(time == 0){ path.moveTo(point.x, point.y) } else { path.lineTo(point.x, point.y) } Log.e("TAG", "getBezierPointsPath: ${point.x} , ${point.y}", ) } return path } /** * 計算在t時刻上，位于貝賽爾曲線上的點的坐標 * @param points 點的集合 * @param t 時刻，屬于0-1 * @return 點坐標 Point */ private fun calcPoint(points: Array<Point>, t: Float): Point{ // 分別求任意兩個點之間的在t時刻運動的距離 // 任意兩點，按照順序分別為始和終 var index = 0 var len = points.size - 1 while (index < len){ points[index].x = getValueByTime(points[index].x, points[index + 1].x, t) points[index].y = getValueByTime(points[index].y, points[index + 1].y, t) index++ if(index == len){ index = 0 len-- } } return points[0] } /** * 定義勻速運動的計算坐標 * @param start 開始的位置 * @param end 結束的位置 * @param time 運動的時間，范圍0-1 * @return time時刻的運動位置 */ private fun getValueByTime(start: Float, end: Float, time: Float): Float{ return start + (end - start) * time } ~~~ 然后使用： ~~~ // 繪圖方法 override fun onDraw(canvas: Canvas?) { super.onDraw(canvas) canvas?.apply { val points = arrayOf(Point(200f, 400f), Point(100f, 20f), Point(500f, 20f), Point(800f, 400f)) val numberOfPoint = 100 mPath = getBezierPointsPath(points, numberOfPoint) drawPath(mPath, mPaint) } } ~~~  很明顯，這里細粒度不夠。可以把numberOfPoint 設置的更大些。當設置為1000的時候：  當然這里可以使用arrayOf的時候添加更多的點，以做到更加高階的貝塞爾曲線，比如簡單修改一下： ~~~ val points = arrayOf(Point(200f, 400f), Point(100f, 20f), Point(500f, 20f), Point(800f, 400f), Point(1000f, 20f) ) ~~~ 也就是對應三個控制點，對應四階本塞爾曲線，對應效果：  當然，在系統中其實也提供了一、二、三階的貝賽爾曲線的API，所以通常直接調用即可。對應的如下： * mPath.lineTo：進行直線繪制 ； * mPath.quadTo(x1, y1, x2, y2) ：生成二次貝塞爾曲線，(x1,y1) 為控制點，(x2,y2)為結束點 ； * mPath.cubicTo(x1, y1, x2, y2, x3, y3)：生成三次貝塞爾曲線， (x1,y1) 為控制點，(x2,y2)為控制點，(x3,y3) 為結束點； # 4. 案例 ~~~ /** * 學習波浪效果，其實也就是移動類似于正弦的連續圖像，帶來的視覺效果 * @author 夢否 * 2022年3月15日 */ class WaterRippleView : View { constructor(context: Context?) : super(context) { init() } constructor(context: Context?, attrs: AttributeSet?) : super(context, attrs) { init() } constructor(context: Context?, attrs: AttributeSet?, defStyleAttr: Int) : super( context, attrs, defStyleAttr ) { init() } private lateinit var mPath: Path private lateinit var mPaint: Paint private lateinit var points1: Array<MyPoint> private lateinit var points2: Array<MyPoint> class MyPoint(var x: Float, var y: Float) /** * 初始化方法 */ private fun init() { mPath = Path() mPaint = Paint() mPaint.isDither = true mPaint.isAntiAlias = true mPaint.strokeWidth = 5f mPaint.color = Color.GRAY mPaint.style = Paint.Style.FILL val viewWidth = resources.displayMetrics.widthPixels points1 = arrayOf( MyPoint(0f * viewWidth, 200f), MyPoint(.33f * viewWidth, 20f), MyPoint(.66f * viewWidth, 360f), MyPoint(1f * viewWidth, 200f) ) points2 = arrayOf( MyPoint(-1f * viewWidth, 200f), MyPoint(-.66f * viewWidth, 20f), MyPoint(-.33f * viewWidth, 360f), MyPoint(0f * viewWidth, 200f), ) // 三階貝塞爾曲線，傳入0，也就是初始時刻 updatePathByDistance(0f) } override fun onDraw(canvas: Canvas?) { super.onDraw(canvas) canvas?.apply { drawPath(mPath, mPaint) } } /** * 根據距離來進行更新在貝賽爾曲線中的點的坐標值 * @param distance 傳入的距離 */ private fun updatePathByDistance(distance: Float) { // 重置 mPath.reset() // 設置 mPath.moveTo(points2[0].x, points2[0].y) mPath.cubicTo( points2[1].x + distance, points2[1].y, points2[2].x + distance, points2[2].y, points2[3].x + distance, points2[3].y ) mPath.cubicTo( points1[1].x + distance, points1[1].y, points1[2].x + distance, points1[2].y, points1[3].x + distance, points1[3].y ) val y = resources.displayMetrics.heightPixels mPath.lineTo(points1[3].x, y.toFloat()) mPath.lineTo(points2[0].x + distance, y.toFloat()) mPath.lineTo(points2[0].x + distance, points2[0].y) } /** * 一直移動繪制的兩個類似于正弦函數的路徑 */ var startedMove = false private fun startMove() { startedMove = true val animator = ValueAnimator.ofFloat(0f, resources.displayMetrics.widthPixels.toFloat()) animator.duration = 800 // 線性插值器，使之勻速運動 animator.interpolator = LinearInterpolator() // 循環 animator.repeatCount = ValueAnimator.INFINITE animator.addUpdateListener(object : ValueAnimator.AnimatorUpdateListener { override fun onAnimationUpdate(animation: ValueAnimator?) { val value = animator.getAnimatedValue() updatePathByDistance(value as Float) // 重繪 invalidate() } }) animator.start() } override fun onTouchEvent(event: MotionEvent?): Boolean { super.onTouchEvent(event) var flag = false when (event?.action) { MotionEvent.ACTION_DOWN -> { flag = true if(!startedMove) startMove() } MotionEvent.ACTION_MOVE, MotionEvent.ACTION_UP -> { flag = false } } return flag } override fun onMeasure(widthMeasureSpec: Int, heightMeasureSpec: Int) { super.onMeasure(widthMeasureSpec, heightMeasureSpec) val minHeight = dp2px(300) val minWidth = dp2px(500) val widthSize = getMeasureSize(widthMeasureSpec, minWidth.toInt()) val heightSize = getMeasureSize(heightMeasureSpec, minHeight.toInt()) setMeasuredDimension(widthSize, heightSize) } /** * 計算高度和寬度 */ private fun getMeasureSize(Spec: Int, minValue: Int): Int { var result = 0 // 獲取模式 val mode = MeasureSpec.getMode(Spec) val size = MeasureSpec.getSize(Spec) // 判斷一下 when (mode) { MeasureSpec.AT_MOST -> { result = Math.min(size, minValue) } MeasureSpec.UNSPECIFIED -> { result = minValue } MeasureSpec.EXACTLY -> { result = size } } return result } /** * dp轉換為px */ private fun dp2px(size: Int): Float { return resources.displayMetrics.density * size } } ~~~