[TOC]
## 概述
* 回溯法是一種通過探索所有可能的候選解來找出所有的解的算法。如果候選解被確認不是一個解的話(或者至少不是最后一個解),回溯算法會通過在上一步進行一些變化拋棄該解,即回溯并且再次嘗試。
* 回溯算法就是個多叉樹的遍歷問題
解決一個回溯問題,實際上就是一個決策樹的遍歷過程
1. 路徑:也就是已經做出的選擇。
2. 選擇列表:也就是你當前可以做的選擇。
3. 結束條件:也就是到達決策樹底層,無法再做選擇的條件。
回溯算法框架
```
result = []
def backtrack(路徑, 選擇列表):
if 滿足結束條件:
result.add(路徑)
return
for 選擇 in 選擇列表:
做選擇
backtrack(路徑, 選擇列表)
撤銷選擇
```
> 其核心就是 for 循環里面的遞歸,在遞歸調用之前「做選擇」,在遞歸調用之后「撤銷選擇」
如枚舉 1,2,3,列出回溯算法的「決策樹」
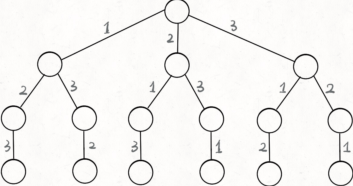
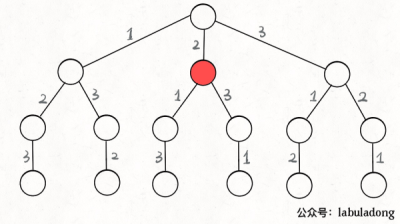
現在可以解答開頭的幾個名詞:\[2\] 就是**路徑**,記錄你已經做過的選擇;\[1,3\] 就是**選擇列表**,表示你當前可以做出的選擇;**結束條件**就是遍歷到樹的底層,在這里就是選擇列表為空的時候。
**前序和后續后序排列**
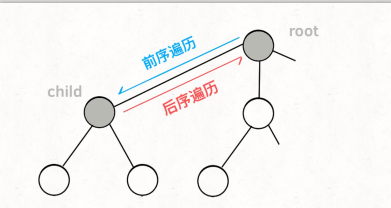
前序遍歷的代碼在進入某一個節點之前的那個時間點執行,后序遍歷代碼在離開某個節點之后的那個時間點執行。
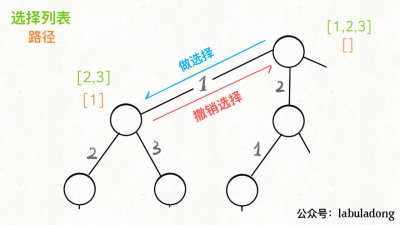
這樣可以更好的理解回溯算法
```
for 選擇 in 選擇列表:
# 做選擇
將該選擇從選擇列表移除
路徑.add(選擇)
backtrack(路徑, 選擇列表)
# 撤銷選擇
路徑.remove(選擇)
將該選擇再加入選擇列表
```
我們只要在遞歸之前做出選擇,在遞歸之后撤銷剛才的選擇
回溯算法 go 實現
<details>
<summary>server.go</summary>
```
import (
"fmt"
)
var group [][]int
func permute(nums []int) [][]int {
group =make([][]int,0)
if len(nums) == 0 {
return group
}
// 存儲已經用過的值,遍歷共用一個 狀態
used := make([]bool, len(nums))
track := make([]int, 0,len(nums))
backtrack(nums, track, used)
return group
}
func backtrack(nums []int, track []int, used []bool) {
if len(nums) == len(track) {
tmp := make([]int, len(track))
// 拷貝切片值
copy(tmp, track)
group = append(group, tmp)
return
}
for i := 0; i < len(nums); i++ {
if !used[i] {
used[i]=true
track = append(track, nums[i])
backtrack(nums,track, used)
// 撤銷狀態
used[i]=false
track=track[:len(track)-1]
}
}
}
func main() {
fmt.Printf("%+v\n", permute([]int{1,2,3}))
//[[1 2 3] [1 3 2] [2 1 3] [2 3 1] [3 1 2] [3 2 1]]
}
```
</details>
<br/>
回溯算法的一個特點,不像動態規劃存在重疊子問題可以優化,回溯算法就是純暴力窮舉,復雜度一般都很高點贊
- 目錄
- Lua
- 常用接口
- 協同程序
- 文件IO
- 錯誤處理
- 面向對象
- Scheme / Racket
- 技巧
- 如何設計遞歸
- 導入自定義文件
- []與() 的區別
- 打印函數
- 函數實現設計訣竅
- trace 打印調試信息
- 命令
- racket 運行
- raco 打包
- 語法
- 向量 / 結構體 / cons / list / string?等檢查類型
- 符號 / 字符 / 字符串
- if / and / cond 條件分支
- 類型判斷 / 等式判斷
- local 組織函數
- 測試函數
- Rust
- 命令
- rustup
- Cargo
- rustc
- Rustfmt
- C++
- 快速入門
- 技巧與概念
- pragma comment
- socket 編程
- 編譯
- 引入庫的 <> 與 "" 的區別
- 語法
- 基礎類型
- 運算符表
- 運算符重載
- 命名空間
- const和mutable的使用
- c++1新特性
- nullptr / constexpr (c++ 1x)
- auto / decltype 類型推到 (c++ 1x)
- 循環數組 區間迭代
- if-switch-變量聲明強化
- 面向對象
- 原始字符串字面量 R"
- 指針
- 內存泄漏
- 指針與引用的差別
- const修飾指針
- 智能指針
- 數組
- 對象
- 構造函數
- 虛繼承/虛基類
- 虛函數和純虛函數
- 抽象類
- 棧中實例化 / 堆實例化
- 實例類型轉換
- 繼承 公有 / 私有 / 保護
- 子類調用父類
- 多重繼承
- 實例指針(this)
- 友元函數 訪問類私有和保護的成員
- 構造函數、explicit、類合成
- 多態的應用
- new和delete的使用
- 函數
- 引用傳值/指針傳值
- inline函數
- Lambda 表達式
- 模版
- 函數模版
- 類模板
- 容器
- std::array
- std::vector
- std::ist / std::forward_list
- map 各種map
- 各種 set
- 元組
- 正則
- 并發
- thread
- 鎖
- 異步訪問
- 條件變量
- 原子操作
- 命令
- g++
- make
- vcpkg
- clang++
- pkg-config
- 常用實例
- fork 方式創建后臺進程
- 第三方庫
- folly 工具庫
- QxOrm
- catch 測試框架
- MSYS2
- pacman
- c++ 性能追蹤
- gperftools
- gprof
- Qt
- Qt 代碼風格
- qt 項目框架
- Qt Design Studio
- 技巧
- 添加 .pri 項目
- 添加子項目
- 加載第三方庫
- 中文不亂碼
- 信號和槽
- 國際化
- 定制幫助系統
- 多媒體
- 數據驗證器
- 伙伴快捷鍵
- 單詞補全
- QPushButton 樣式問題
- 為元素添加滾動條
- 指定圖標
- 自定義的結構體支持串行化
- 界面數據存儲與獲取
- 匿名函數
- 預編譯
- 升級瀏覽器內核
- 封裝彈窗
- 命令
- qmake
- 命令行編譯
- pro 文件
- CONFIG
- TEMPLATE
- windeployqt 打包
- jom
- 知識
- 元對象系統(MOC)
- 對象樹與擁有權
- 各個 TextEdit 的區別
- Qt 資源系統
- QSS 查詢
- QObject的創建時間
- qt 的繼承關系
- 單元測試
- 宏
- 測試類/函數
- GUI測試
- Benchmark測試
- 實例
- 在子項目中創建
- 數據驅動測試程序'
- 模擬GUI事件
- API
- 控件
- QInputDialog
- QIcon
- QFileIconProvider 提供文件icon
- QActionGroup
- QSystemTrayIcon
- QMenu
- QWidget
- QLabel
- QTextBrowser
- QTextEdit
- QPushButton
- QRadioButton
- QDockWidget
- QMainWindow
- QKeySequence 預設快捷鍵
- QSplashScreen 啟動圖
- QListWidget
- QTreeWidget
- QTreeView
- QTreeWidgetItem
- QTreeWidgetItemIterator 遍歷QTree
- QTableWidget
- QTableView 基類
- QTableWidgetItem
- 條目控件
- 條目的拖拽
- 自定義右鍵菜單
- 基于條目控件的樣式表
- QWebEngineView
- 模型
- QFileSystemModel 文件系統
- QStandardItemModel
- QAbstractItemModel 基類
- QAbstractItemView / QStandardItem
- QSortFilterProxyModel
- 布局
- 布局分類
- QSplitter 分裂器
- QSizePolicy 伸展
- 伸展因子
- 伸展策略
- BoxLayout 布局
- FlowLayout 流式布局
- QGridLayout 柵格布局
- QFormLayout 表單布局
- 文件系統
- QFile
- QFileInfo
- QStorageInfo 分區信息
- QTemporaryDir
- QTemporaryFile
- QDir
- QFileSystemWatcher 監控文件
- QLockFile
- 字節與流
- QByteArray
- QDataStream
- QTextStream
- 進程
- QProcess
- 線程
- QMutex
- QReadWriteLock
- 并發方案
- 繼承 QObject [推薦]
- 繼承 QThread
- QRunnable與QThreadPool 配合
- QtConcurrent
- Application::postEvent
- 圖像
- QPainter
- QPixmap / QBitmap
- QImage
- QPicture
- QImageWriter 創建圖片
- QImageReader 讀取圖片信息
- 命令行工具
- QCommandLineParser
- 關聯容器
- QStack
- QVector
- QLinkedList
- QQueue
- QList
- ====== 順序容器 ======
- QMap
- QHash
- QMultiMap 一key 多value
- QMultiHash 一key多value
- QCache key映射到類
- QPair
- QSet
- ====== 關聯容器 ======
- QVariant
- QVariantList
- QVariantMap
- QMetaObject 元對象,反射
- invokeMethod
- 實例
- 反射類名
- 反射實例
- 數據庫
- mysql 鏈接
- sqlite 內存版
- QSqlDatabase 連數據庫
- QSqlQuery
- QSqlTableModel 綁定表
- QSqlQueryModel
- 日志
- myMessageOutput 自定義日志格式
- 網絡
- QLocalServer/QLocalSocket
- QTcpServer / QTcpSocket
- QNetworkAccessManager 異步API
- QSslSocket
- QUdpSocket
- QUrl
- QUrlQuery
- 系統
- QStandardPaths
- QDesktopServices 桌面服務
- QSysInfo
- 日期和時間
- QDate
- QDateTime
- QTime
- 異常處理
- QException
- 正則
- QRegExp
- 字符串
- QStringRef
- QUuid
- Core
- Q_PROPERTY 屬性
- QGlobalStatic
- QSharedData
- QCoreApplication
- 全局 qxxx
- qSort / qStableSort 排序
- qRegisterMetaType 注冊自定義類型
- qSetMessagePattern 改qDebug格式
- qInstallMessageHandler
- QCryptographicHash 加密
- QSettings
- QTimer
- QObject
- 設計模式
- 工廠類
- 單例模式
- 第三方庫
- FluentUI UI框架
- Felgo 可做移動端
- Dart
- 語法
- 基礎類型
- 運算符
- 函數
- 類
- 控制流程語句
- 異常
- 映射
- 異步支持
- Future / Stream
- async/await
- 容器
- Map
- List
- Set
- 庫和可見性
- 測試
- pub / pubspec.yaml
- Flutter
- 安裝
- 技巧
- 混合開發方案
- State Widget 生命周期
- 與原生通信
- 自動切換Andrio和Ios 主題
- 命令
- flutter
- flutterfire 構建 Firebase
- 常見組件
- 布局
- 響應式
- 交互
- cupertino IOS 風格
- 資源與圖片
- Packages
- 路由
- Builder
- streambuilder
- theme
- 三方庫
- Getx 狀態管理
- shared_preferences 存儲
- webview_flutter
- FluroRouter 路由
- 實例
- 放大圖片
- Python
- 技巧
- 語法
- 字符串
- 字典
- 裝飾器
- 類
- 異常和錯誤
- 異步 python 3.x
- 場景
- 文件讀取
- 內置包
- 包
- 工具類
- Supervisor-Linux/Unix進程管理工具
- 網絡
- urllib包
- requests-比urllib2簡潔
- BeautifulSoup-解析html
- 數據庫/ORM
- pymysql -python3的mysql庫
- SQLAlchemy ORM
- 辦公
- pdfminer3k-解析pdf
- 測試 & 安全
- faker -測試
- web 框架
- web.py框架
- Django框架
- 模型
- gui
- easygui_gui模塊
- tkinter - 高效簡單
- pyqt5 - 控件豐富
- 單元測試
- doctest模塊
- unittest模塊
- 命令
- pip
- poetry 高級pip
- virtualenv 虛擬環境
- Java
- java 數組
- java 類
- java 包
- java 異常
- java String
- java 集合
- PHP
- 常用場景 / 封裝
- appkey/secretKey 實例
- https雙向認證
- 從字符串中找出高頻詞
- 操作 HTML DOM
- levenshtein 輸出錯誤,猜測輸入的值
- ip 查詢
- 配置webhook.php
- php 輸出圖片
- ignore_user_abort 網頁斷開有效
- 原生支持異步的方法 exec
- 可自動結束的程序
- 循壞程序
- ===== 函數 / 類封裝 ? =======
- 指定月份的第某個月
- 時間類封裝 某天的開始與結束
- 數據庫鏈式調用封裝
- curl 封裝 / 發送文件 / 遠程下載到服務器
- 下載進度條 / 斷點續傳
- 獲取 win / linux 的mac地址
- exec 控制 cli 服務器的啟動與停止 linux 版本
- 代碼規范及技巧
- PHP的優化之道
- PHP 代碼簡潔之道
- PHP The Right Way
- PHP標準規范
- PSR-3 日志接口規范
- PSR-4 自動加載規范
- PSR-6 緩存接口規范
- PSR-7 HTTP 消息接口規范
- PSR-11 容器接口
- PSR-13 超媒體鏈接
- PSR-14 事件分發器
- PSR-15 HTTP 請求處理器
- PSR-16 緩存接口
- PSR-17 HTTP 工廠
- PSR-18 HTTP 客戶端
- PHP注釋規范
- php7+
- PHP WEB框架
- Slim 微型框架
- yaf
- RPC-yar
- 內置函數
- hyperf 高性能框架
- swoole
- 安裝
- HttpServer
- WebSocket
- AsyncIO
- Swoole-Crontab
- 異步文件系統IO
- 異步Redis
- 異步MySQL客戶端
- process
- Memory 內存操作
- Channel 連接池
- swoole與tp5
- 調試 swoole
- 示例
- websocket 綁定對象方法
- redis 事件訂閱發布
- EasySwoole
- 技巧
- 對自定義類優化的方式
- 數據庫
- 基礎使用
- 定時器
- 自定義命令
- 自定義進程
- 自定義事件
- 異步任務
- Crontab 定時任務
- 日志
- 組件庫
- 單例模式
- Di 容器 / 依賴注入
- 協程 / WaitGroup
- 內存 Table
- Csp 并發等待執行
- 隊列 Queue
- SplArray
- SplBean 過濾表結構
- 緩存
- 熱重啟
- 控制器
- TP5
- 驗證器
- 內置規則
- 數據庫操作
- 數據添加或更新
- 靜態增刪改查 / 關聯操作
- 日志操作
- 路由
- taglib-自制標簽
- migrations 數據庫遷移
- tp 測試
- TP3.2
- 數據庫操作
- 關聯表
- 增刪改查與驗證
- 前置與后置
- 發送郵箱
- Tp6
- 技巧
- 多應用的api版本控制
- phinx 遷移工具
- 單元測試
- 先使用修改器在驗證
- 異常統一處理
- thinkcmf
- 快速入門
- 常用插件
- 小程序管理插件
- 手機微信登錄插件
- 表單自動生成插件
- phalcon C框架
- 快速入門
- 腳手架教程
- Symfony
- Swoft
- laravel
- webman
- workerman
- Spiral Framework
- composer / C擴展
- 網絡 / curl / 文件上傳 / jwt 認證
- guzzle [19.8k] http 客戶端
- php-curl-class[2.6k] 封裝curl為類
- class.upload.php 文件上傳
- codeguy/upload 文件上傳
- php-jwt 封裝 JWT 加解密
- 文本 uuid / 加密整數id / 中文轉拼音 / 解析html
- uuid 生成uuid
- hashids 隱藏真實id
- pinyin 中文轉拼音
- html-parser 類jquery解析 html
- i18n
- i18n 國際化
- gettext 國際化
- 數據驗證 / mock數據 / 媒體類型
- faker 生成驗證數據
- Analyzer 檢驗媒體資源類型
- Valitron [1.3k] 數據驗證
- rakit/validation [399 star] 驗證數據
- 支付
- OmniPay 多網關支付處理的框架
- 時間
- Carbon [14.6K]
- 日志 monolog / seasLog
- monolog php編寫
- SeasLog C擴展
- 辦公文件 pdf / word / excel / ppt
- Snappy 一個PDF和圖像的生成庫
- WKHTMLToPDF HTML轉換為PDF
- PHPPdf XML轉化為PDF和圖片
- PHPWord - 處理Word文檔
- PHPExcel 處理Excel文檔
- PHPPowerPoint -處理PPT幻燈片
- 性能分析 xhprof
- xhprof - PHP性能追蹤及分析工具
- 緩存 yac
- Yac 5.2+ 共享緩存
- 配置 yarconf / 解析 json xml ini yaml
- yarconf 7.0+ 讀取配置
- config 解析 json xml ini yaml
- 隊列 resque (基于redis) / beanstalkd
- Beanstalkd 隊列
- php-resque 基于redis的消息隊列
- web ui 管理 / redis / pgsql / mysql / mgdb
- phpRedisAdmin - Redis 管理
- phpPgAdmin - PostgreSQL管理工具
- phpMyAdmin - MySQL管理工具
- rockmongo - MongoDB管理工具
- ORM
- medoo 支持5大數據庫
- Redis C 擴展
- mongodb C擴展
- mongo-php-library 官方基于C擴展到的封裝
- MongoDB ORM
- ElasticSearch PHP 用于 ElasticSearch 的官方客戶端庫.
- 調試與性能
- nette/tracy 優化報錯
- 狀態機
- Finite 有限狀態機
- 定時任務
- jobby
- 郵箱
- php-imap 接收郵箱
- PHPMailer 發送郵箱
- Sphinx - 全文索引
- JsonMapper 一個將內嵌JSON結構映射到PHP類上的庫
- weichat 封裝
- User Agent 檢測
- class.upload.php 文件上傳
- 官方庫
- SPL 數據結構
- SplDoublyLinkedList 鏈表
- SplStack 棧
- SplQueue 隊列
- SplHeap 堆
- SplMaxHeap / SplMInHeap 大排序
- SplObjectStorage 存儲對象列表
- SplFixedArray 固定長度的數組
- 預定義接口
- Iterator while迭代
- ArrayAccess 數組式接口
- Serializable 序列化接口
- IteratorAggregate foreach迭代器
- Observer 觀察者
- SPL 函數
- spl_autoload_register 自動導入類
- class_parents 返回指定類的父類
- spl_object_hash/spl_object_id
- SPL 常見異常
- SPL 迭代器
- DirectoryIterator 文件目錄迭代器
- FilesystemIterator 文件迭代器
- GlobIterator 帶匹配的文件系統
- ArrayIterator 把數組改成迭代器
- NoRewindIterator 只遍歷一次
- RecursiveArrayIterator 遞歸迭代
- RecursiveTreeIterator 輸出遞歸樹
- SPL 文件處理
- SplFileInfo 文件信息
- SplFileObject 文件操作提供對象
- SplTempFileObject 臨時文件
- Ctype 類型檢測
- ctype_alnum 是否只有字母和數字
- ctype_alpha 是否是字母
- ctype_cntrl 是否是控制符(\n\t\r)
- ctype_digit 是否是整數
- ctype_lower / ctype_upper 是否是 小/大 寫字母
- ctype_graph 是否是可見字符(空格不算可見)
- ctype_print 是否是可見字符(空格算可見)
- ctype_punct 是否是除字母,數字,空格外的特殊字符
- ctype_space 是否是空白字符
- ctype_xdigit 是否包含16進制字符([0-9 和 [A-Fa-f] ])
- 數組
- array_map-針對多個數組
- array_multisort 對二維數組進行排序
- array_filter
- array_walk - 對一個數組操作
- array_walk_recursive 遞歸
- filter 過濾器函數
- 預定義常量
- filter_has_var 存在指定變量
- filter_var 過濾變量
- filter_var_array
- filter_input_array 過濾外部變量
- filter_input
- 控制輸出 flush
- flush 刷新輸出緩沖
- 實戰
- 安全轉義參數
- htmlspecialchars html標簽轉實體
- addslashes 用反斜線轉義(可用于數據庫)
- quotemeta 轉義特殊字符
- 日期/時間/日歷
- format 參數列表 如 Y,m,d
- DateTime 時間函數
- cal_days_in_month 某個月的天數
- date_parse_from_format [函數] 根據日期格式轉時間
- 異常處理
- set_error_handler
- set_exception_handler 自定義異常
- URL 處理函數
- get_headers 獲取頭信息
- http_build_query 數組轉 query
- parse_url 解析 URL 返回數組
- urldecode 和 urlencode
- 字符串處理
- strstr 字符串的首次出現
- chunk_split 將字符串分割成小塊
- chr / ord 字符與ascii轉換
- str_split 將字符串轉換為數組
- htmlentities / htmlspecialchars 等 html 編解碼
- strip_tags 字符串中去除 HTML 和 PHP 標記
- uniqid 返回唯一值
- preg 函數
- preg_grep 從數組返回匹配的值
- preg_last_error 正則匹配錯誤
- preg_match / preg_match_all
- preg_replace 正則替換
- preg_replace_callback
- preg_split
- 進制轉換
- bin2hex / hex2bin 字符串-16進制
- bindec / decbin 十進制-二進制
- octdec / decoct 八進制-十進制
- base_convert 任意進制轉換
- 文件系統函數
- fopen / feof / fclose 適合文件和網頁
- fread 按字節讀取
- fgets 按行讀取
- fwrite 寫入文件
- file 一次讀取整個內容,行遍歷
- fscanf() 每行都根據格式循環輸出
- file_get_contents 一次讀取所有,返回完整字符串
- flock 文件鎖
- disk_total_space 磁盤容量
- 文件 / 路徑處理
- scandir 返回指定路徑的目錄和文件
- glob 使用 * 模糊搜索文件和目錄
- is_dir / is_file
- opendir / readdir / closedir 循環輸出文件/目錄名
- dirname /basename 父路徑 / 基礎文件
- pathinfo 文件路徑的信息
- realpath 真實路徑
- copy / rename 復制 / 重命名
- touch / unlink 創建/刪除
- file_exists 文件是否存在
- filesize 獲取文件大小
- is_readable / is_writable / is_executable
- 文件權限
- fileperms 獲取文件權限
- 反射
- ReflectionClass 反射類
- ReflectionExtension 反射擴展
- ReflectionFunctionAbstract
- ReflectionFunction 反射函數
- ReflectionParameter 函數,類的參數
- ReflectionProperty 類屬性
- ReflectionType 參數或返回值的類型
- 協議
- php://
- input / output
- stdin / stdout / stderr
- memory / temp
- filter
- ftp:// 和 ftps://
- data://
- glob:// 文件路徑模式
- 過濾器
- 字符串過濾器
- 轉換過濾器
- stream
- Stream Filters
- Contexts
- socket
- PDO
- PDO::setAttribute 屬性
- 加密擴展
- password_?hash
- openssl
- 雜項函數
- sys_getloadavg 獲取系統的負載
- hrtime 微妙時間戳
- ignore_user_abort
- uniqid
- sleep/usleep
- imap 郵箱
- Session
- Callback 類型
- exec 執行結果以數組返回
- socket_create 操作
- soap 調用 webserver
- C / C++框架 編寫擴展
- 原生編譯
- 引用 加載動態庫(.so) 文件
- 參數、數組和Zvals
- Zephir 開發PHP擴展
- 安裝
- 快速入門
- php-cpp C++開發擴展
- 安裝
- 技巧
- 語法
- 變量
- 常數
- 輸出和錯誤
- 函數
- 指定參數
- 調用PHP函數
- Lambda函數
- 構造函數
- 魔術方法
- 基礎SPL接口
- 擴展類的魔術方法
- 類屬性
- 異常
- 讀取php.ini變量
- 擴展回調
- 命名空間
- FFI PHP擴展方式
- pear / pecl
- pecl c 擴展
- 在多 php 版本中指定
- pear php 擴展
- 安裝/編譯
- oneinstack 一鍵配置
- lnmp /lamp 腳本安裝
- 配置 Let's Encrypt
- 配置 thinkphp
- dnmp docker 安裝 LNMP
- ==== php 環境一鍵安裝 ====
- Centos
- Ubuntu
- macOS
- ==== 包安裝 ====
- apache
- nginx
- php
- 安裝 GD 擴展
- 安裝 openssl 模塊
- ==== 編譯環境安裝 ====
- window apache/php
- window nginx/php
- PHPUnit
- 編程寫測試
- 添加測試的依賴
- 數據供給器
- 對異常進行測試
- 對輸出進行測試
- 基境 測試初始化與還原
- 數據庫測試
- php 擴展
- opcache 緩存編譯
- 常用正則
- php.ini 最佳實踐
- php 調用 jar包
- Golang
- 知識碎片
- 無鎖編程
- 調度器
- 預防CSRF攻擊
- 避免XSS攻擊
- 避免SQL注入
- 存儲密碼
- 設計模式 / 規范 / 性能 / 技巧
- 設計模式
- 單例模式-數據庫單例
- 值選項模式
- 組合模式
- 策略模式
- 規范
- 性能優化
- 技巧
- 高性能
- 字符串拼接性能
- 切片性能及陷阱
- for 和 range 的性能比較
- Reflect 提高反射性能
- 逃逸分析
- 死碼消除與調試(debug)模式
- sync.Mpap 與 加鎖map
- 項目布局
- 項目布局一
- 項目布局二
- DDD分層架構
- 數據類型
- 切片類型( slice)
- 場景
- 請求/響應/錯誤碼設計
- gin 對 handle的封裝
- 帶超時的 sync.WaitGroup
- 優雅關閉協程
- 控制協程的并發數量
- 并發非阻塞緩存
- 守護其他進程的代碼
- 各類型轉 sturct
- 注冊為window 的服務
- go 注冊
- sc 注冊
- nssm 注冊
- udp 打洞
- udp 打洞轉 tcp
- Reader 用法
- i18n 本土化
- 壓縮編譯體積
- 第三方庫
- 操作 DOM
- goJquery 像 jQuery一樣操作DOM
- ORM
- gorose -鏈式調用
- GORM
- 技巧
- 獲取一對多
- dbx 支持緩存全表數據
- sqlx
- 路由 / http客戶端 / websocket
- httprouter 實現RESTful 風格
- mux - 路由
- fasthttp 比 net/http 快10倍
- GoRequest http 客戶端
- gorilla庫 路由 /參數轉結構體
- gorilla/mux URL路由和分發器
- gorilla/schema 參數轉換為結構
- websocket
- balloons-websocket 封裝好的 websocket
- melody 優雅的websocket
- nhooyr-websocket 性能好于gorilla
- gorilla/websocket [14.5K]
- 緩存 / 并發
- go-redis
- gocache 封裝 redis,memcached,內存的緩存
- cache2go 帶過期回調的緩存
- go-cahce 類memcached 可存文件斷電恢復
- tiedot 內存NoSQL數據庫
- Gcache 帶過期,帶操作事件,支持 LFU,LRU ,ARC
- concurrent-map 支持并發的map
- bigcache 分片map緩存,value 只能存byte
- golang-set set的go實現
- atomic 支持更多類型
- conc 更好的結構化并發
- map轉struct / 打印結構體
- mapstructure map 轉 struct
- litter 優雅打印結構體
- 數據結構
- 結構算法庫 Lists / Sets / Stacks / Maps / Trees
- 工具庫
- pie 常用數組操作
- lo 類似 Lodash
- 連接池
- go-common-pool
- ants
- 序列化庫 json / ini / yaml
- jsoniter 官方更高效的 json 庫
- easyjson免運行時反射的json化
- gjson 從json中取值或判斷
- simplejson 處理未知結構的json
- props 解析各種 ini / yaml 等
- 支持Unmarshal map 轉配置
- viper 11k Star 支持yaml,ini 支持 env ,命令行 等
- hash / uuid
- xxhash 返回整數類型
- uuid
- Log 日志庫
- zap 高性能日志
- Logrus 可插拔日志
- GUI
- fyne 簡單難看的 GUI
- go-qt
- wails 桌面gui go + vue
- webview 用 html 可直接編譯跨平臺 app
- vugu vue+WebAssembly
- termui [11.6k]
- 命令行 / TUI
- urfave/cli [14.3k] 命令行
- kingpin 簡單強大命令行
- cobra [18.2k] 專業級命令工具
- x-mod/cmd 空格隔離參數
- mpb 進度條
- progressbar 另一個進度條
- rivo/tview [4.5k] 命令行ui
- cute 漂亮的輸出
- bubbletea 強大的 TUI
- 檢驗 validator
- validator
- 定時器
- cron 簡單,不可修改的定時器
- cronlib 可修改任務 推薦
- robfig/cron 支持cron 和 固定時間
- 加密庫
- thinkoner/openssl 可支持 ECB、CBC等
- 自己封裝的加密庫
- 身份驗證和OAuth
- authboss 認證
- go-oauth2-server 符合規范的OAuth2服務器
- 開源 IM
- tonyboxes/imgo
- GoBelieveIO/im_service
- alberliu/gim [1.2k]
- 流量控制 / 熔斷器 / 容錯
- hystrix-go
- 示例
- Hello World
- http 示例
- dashboard 可視化
- Sentinel GO 流量控制組件
- QPS
- 熱點參數限流
- 熔斷降級
- 靜態資源打包
- go-bindata 靜態資源打包進執行文件
- 爬蟲/無頭瀏覽器
- colly [11.9k]
- chromedp 可控制是否顯示瀏覽器[9.6k]
- 實例
- 啟動訪問某個網站
- 訪問網站并且截圖
- 設置cookie,保持登錄狀態
- 下載文件
- emulate 設備模擬
- 代理
- goproxy 代理
- 聊天機器人
- chatbot
- 圖像
- imaging 圖像處理
- gg 圖像處理
- 單元測試
- gomonkey 打樁函數 - 推薦
- goconvey 測試結果帶UI
- sqlMock
- redisMock
- httpmock
- Testify 支持斷言,寫法更簡便
- gocheck 測試框架
- faker 生成假數據
- 依賴注入
- fx User開發的依賴注入
- 注冊一個http
- 添加 handle
- 添加日志
- 注入接口
- 注入多個接口
- MIME 文件檢測
- mimetype 類型檢測 [1.2k]
- filetype [1.9k]
- 全文索引
- bleve
- fsnotify 文件監聽
- gopay 支付集合
- .env 環境變量
- 哈希算法 轉整數
- gopsutil 系統性能數據
- 官方包
- C
- 簡單調用 c函數
- c與go 類型轉換
- go 類型轉C類型
- panic / recover
- panic+recover簡化錯誤處理 模塊必學
- error 自定義錯誤結構體
- unsafe
- archive
- tar
- zip
- bufio
- bytes
- compress 壓縮
- gzip
- zlib
- container 數據結構
- heap
- list
- ring
- index/suffixarray 字典樹
- Context
- crypto 加密
- rsa
- md5
- sha1
- sha256
- sha512
- tls
- database
- sql
- encoding
- encoding
- base32
- base64
- binary 序列化
- csv
- gob
- hex
- json
- xml
- errors
- expvar - 線性安全全局變量
- flag
- fmt
- 格式化輸出格式
- html
- html
- template
- image
- image
- color
- png
- draw 圖像合成函數
- gif
- jpeg
- io
- io
- ioutil
- log
- syslog
- math
- math
- rand
- net
- net
- http
- cookiejar 自動存儲cookie
- httptest http的mock
- httptrace 追蹤http
- httptest
- httputil 反向代理,打印頭信息
- pprof
- rpc
- smtp
- url
- textproto
- os
- os
- exec
- signal
- user
- path
- path
- filepath
- plugin
- reflect
- regexp 正則
- runtime
- runtime
- debug
- pprof
- trace
- sort
- strconv
- strings
- sync
- atomic
- testing
- doc
- testing
- quick
- text
- scanner
- template
- time
- unicode / utf8
- unicode
- utf8
- utf16
- embed 嵌入
- js WebAssembly
- 示例
- golang.org/x
- net
- ctxhttp 帶 ctx 的請求
- nettest
- netutil
- websocket
- oauth2
- crypto
- ssh
- text
- xorm / xorm+odbc
- go 適配 odbc
- 其他技巧
- 查詢條件方法
- 關聯查詢
- 緩存
- 增刪改查前后置的操作
- 同時支持三個數據庫需求
- cmd 自動生成結構
- 嵌入 logrus
- web框架 / 微服務框架
- gin 框架
- 語法
- 中間件
- 參數模型綁定
- hmtl 渲染
- JSONP
- BasicAuth 基礎認證
- 路由
- 輸出格式
- 重定向
- 異步處理
- 靜態資源
- 實例
- HelloWorld
- go-gin-example
- gin-vue-admin
- 測試
- beego
- 模型操作
- generate 生成的模型操作
- 一對一查詢
- 一對多
- 打印日志
- 路由
- iris web 框架
- kratos bilibili 開源
- gf web/tcp 4.3K集大成框架
- gf-cli 命令行工具
- tcp 組件
- endless 熱更新
- echo
- ====== web 庫 ======
- Goji微框架
- go-zero [5.2k] web / 微服務框架
- go-micro 14.9K 微服務框架
- 快速開始
- 技巧
- 命令
- micro
- dashboard
- 示例
- HelloWorld
- 用戶模塊示例
- Jupiter 2.5K 微服務框架
- ====== 微服務 ======
- go-admin
- Gin-Vue-Admin
- gfast
- Simple Admin
- ====== Admin 后臺 ======
- RPC / ARPC
- net/rpc
- net/rpc/jsonrpc 不支持http
- RPCX 分布式的RPC
- 元數據 / 分組
- 心跳
- 單服務例子
- 多服務例子
- 異步回調例子
- Fork 發送多個rpc有個成功
- broadcast 廣播模式
- UI管理工具
- erpc
- arpc
- tcp / tcp 框架
- 最簡單的 tcp 連接
- 面向對象,帶有類型的tcp連接
- tcp binary 設置協議頭
- 完善的tcp 服務端/客戶端管理
- tcp server 框架
- zero - [152]
- xtcp - [101]
- gotcp - [458]
- Zinx - [3K]
- Go Web 編程
- go web
- websocket
- go cli
- godoc
- 約定
- Example
- go build
- buildmode 編譯不同結果
- 編譯 *.so 的動態鏈接
- pgp 示例
- 條件編譯
- +build 條件編譯
- go:build 推薦
- 文件后綴編譯
- go:build 條件編譯
- mod
- gcflags 逃逸分析等
- asmflags
- -ldflags 編譯優化等
- go run
- go install
- go get
- go generate
- go test
- -bench 壓測
- http 測試
- fuzz 模糊測試
- go mod
- go tool trace 性能追蹤
- go tool pprof 性能追蹤[推薦]
- 封裝 pprof 可指定端口
- statsviz 運行時統計信息
- go tool dist
- work
- 編譯工具
- xgo 一鍵編譯多平臺
- goreleaser 快速上傳各架構編譯到github
- go 國產化編譯
- air 監聽go,實時編譯
- golines 自動換行
- go 支持 oracle
- go 調用dll
- dlv 遠程調試
- 服務器
- Git
- 知識
- codeowners 指定目錄所屬
- 命令
- config
- commit
- rebase 合并 commit
- merge 分支合并
- cherry-pick
- checkout 切換/創建分支
- branch 創建/刪除分支
- clone
- diff
- reset
- revert 取消某個提交
- rm / mv
- mergetool 可視化合并沖突
- log / reflog
- stash 擱置
- tag
- show
- pull / fetch
- push
- remote
- submodule 子模塊
- shortlog log日志匯總
- archive 打包
- sparse-checkout
- git lfs 管理大文件
- rev-list
- filter-branch 歷史中刪除不該提交的文件
- bisect 二分查找
- format-patch 導出補丁
- worktree 便捷clone
- 技巧
- HEAD^ / HEAD~ 差別
- git 使用 rsa
- window 重新設置賬戶密碼
- commit 規范
- 生成 Change log
- 規范流程
- commit 圖標
- 分支命名
- centos git 服務器
- Nginx
- 技巧
- location 匹配
- 場景
- http 代理 / 超時設置
- 靜態站點 / 動靜分離
- 負載均衡
- 限流配置
- HTTP/2 服務推送
- 匹配路徑跳轉
- 縮略圖
- 優化
- reuseport 負載均衡 [nginx>1.9]
- linux 內核參數優化
- nginx.conf 配置
- open_file_cache
- 自定義 access.log 格式
- Apache
- 常見場景
- .htaccess 場景
- 切割日志
- 改寫重定向權限
- rewrite日志功能
- ip限制
- 目錄列表功能
- 響應頭的 Server 信息
- 代理 / 重定向
- 配置 https
- 添加響應頭信息
- 限制目錄訪問
- 某目錄不解析 php
- 允許跨域
- mpm 三種并行處理模塊
- Caddy 類Nginx
- Caddyfile
- Caddyfile 指令
- root
- header
- php_fastcgi
- rewrite / try_files / uri 代理
- redir 重定向
- encode 壓縮
- basicauth http認證
- handle / handle_path 類似nginx 的location
- reverse_proxy
- metrics 統計
- 場景
- 設置靜態文件
- 自動跳websocket
- 真實域名設置https
- 代理
- php 服務
- 命令
- 監控日志
- OpenResty 帶lua 的nginx
- ====== 常用工具 ======
- protobuf 協議
- 安裝
- protobuf
- gogo
- protoc 命令
- 語法
- proto3的變化
- 示例
- golang 實現
- grpc
- golang 實現
- ====== 傳輸協議 ======
- opentracing 標準
- jaeger UI 優化,更簡單
- 實例
- 帶 context 的追蹤
- 以 span 追蹤
- http 形式訪問
- 使用Inject和在進程之間
- rpcx 調用 [通過 conetxt ]
- rpcx 調用[通過傳遞 string(tranid,spanid,parentSpanId)]
- Zipkin
- ====== 鏈路追蹤 ======
- jenkins 持續集成/交付
- 推薦設置
- 技巧
- webhook -通過gitlab 觸發
- 遠程觸發編譯
- 添加節點
- 構建一個go
- 常用環境變量
- 構建方式
- pipeline
- 設置環境變量
- 實例:Jenkinsfile
- 示例:使用多個agent
- 參數化構建
- MultiJob Project (新版棄用)
- 插件
- Go Plugin 插件
- git 無變化跳過構建
- Folders Plugin 創建任務分組,方便管理
- Multiple SCMs Plugin [新版本棄用]
- 生成時間戳
- FTP 傳送到應用服務器
- Publish Over SSH 發送到遠程
- 角色及權限管理
- 備份
- pipeline
- blue ocean 可視化 pipeline
- junit 測試報告
- Cobertura Plugin 可視化覆蓋率
- cds 持續集成
- Travis CI 教程
- GitLab
- 持續集成 CI/CD
- 安裝Runner環境
- .gitlab-ci.yml 配置
- CI/CD Examples
- 備份還原
- Gitea git 自托管
- ====== 持續集成 ======
- Zabbix 服務器監控
- prometheus 時序處理,報警系統
- 概念
- 工作流程(推薦閱讀)
- 數據類型
- 作業和實例
- 聯合
- 命名
- 安裝
- 組件
- prometheus.yml 配置
- 數據模型
- PromQL
- 運算符
- 函數
- 查詢
- HTTP API
- 記錄規則
- 警報規則
- 配置
- 告警規則
- 示例模板
- Alertmanager
- 配置 Alertmanager
- 實例
- 監控程序啟動
- 監控cpu,內存告警
- 服務發現
- 基于文件的服務發現
- 實例
- 導入 prometheus
- 配置三個 node
- go demo
- grafana 圖形分析器
- Grafana 變量
- 報警
- 配置郵箱接收
- 配置 webhook
- 通知策略
- 實例
- 開源監控方案
- go+influxdb+grafana 制作日志監控系統
- 數據庫中獲取數據展示
- goaccess 日志分析工具
- countly-server 網站統計
- go-netflow 監控程序流量
- tproxy 監測 grpc 與mysql 連接
- Monyog 監控mysql
- uptime-kuma 多功能監控
- kyanos 帶ui 的tcpdump
- ====== 監控 ======
- metersphere 測試/壓測/報告
- ====== 測試 ======
- beats 輕量型日志采集器
- fluentd 日志處理
- 安裝
- 配置文件
- 語法
- 公共參數
- 插件
- 輸入插件
- tail 監聽文件
- forward 接受到其他fluent
- tcp
- http
- exec 接受程序輸出
- monitor_agent 監視器
- 輸出插件
- file
- forward 轉發到其他fluent
- http
- copy
- roundrobin 輪詢輸出
- stdout
- elasticsearch
- mongo
- mongo_replset
- 容器開發
- 實例
- HelloWorld
- PHP應用
- apache日志輸出到mongod
- Addax 異構數據同步
- 示例
- Hello World
- Elasticsearch
- Loki grafana 的日志收集
- ====== 日志/數據 處理 ======
- Bazel 構建
- Make
- 技巧
- ====== 構建工具 ======
- HAProxy
- 安裝與示例
- 配置詳解
- 示例
- 搭建L7負載均衡器
- 搭建L4負載均衡器
- 使用Keepalived實現高可用
- Keepalived 虛擬ip
- ====== 負債均衡 ======
- pyroscope-server pprof 定位性能問題
- 示例
- go 示例
- ====== 持續profiling服務 ======
- proxmox 虛擬機管理
- Vagrant
- opentofu 云化管理,可回滾docker等
- Docker
- 規范的docker部署案例
- 場景
- phpstorm調用docker
- Docker 命令
- docker push / pull
- docker search
- docker images
- docker rmi
- docker commit 定制鏡像
- docker tag 鏡像標簽
- docker save 導出鏡像
- docker history 鏡像創建歷史
- docker buildx 構建多種系統架構
- ====== 鏡像 ======
- docker run
- docker update 更新run的設置
- docker stop / start / restart
- docker pause / unpause 暫停/啟動
- docker kill 殺到運行的容器
- docker rm
- docker attach / exec 進入容器
- docker export / import 導入導出
- docker ps 列出容器
- docker port 映射的端口
- docker top 類似top
- docker logs 容器日志
- docker inspect 容器元數據
- docker stats 資源情況
- docker cp 復制目錄到容器
- docker diff 容器結構變動
- docker rename 重命名
- ====== 容器管理 ======
- docker login
- docker logout
- ====== Docker Hub ======
- docker swarm 管理集群服務
- docker-machine 模擬安裝與使用
- vm 安裝和使用
- docker service
- docker node 管理集群節點
- docker stack 文件方式編排
- 示例:部署WordPress
- ====== 集群管理(Swarm) ======
- docker network
- network create
- network connect
- network disconnect
- network inspect 顯示細節
- network ls
- network prune 刪除所有未使用網絡
- network rm
- docker volume
- volume create
- volume inspect 詳細信息
- volume ls
- volume prune 修剪
- volume rm
- docker system 系統管理
- system df 磁盤總體情況
- system prune 移除不用資源
- system info 等于 docker info
- system events 等于 docker events
- docker info docker 信息
- Docker-compose
- 命令
- docker 命令轉 docker-compose
- Docker-machine 編排
- dokcer-machine create
- 安裝
- Dockerfile 文件
- ENTRYPOINT 入口點
- docker-compose.yml
- 指令
- 私有倉庫
- docker-registry
- Harbor
- UI界面
- lazydocker docker 命令行ui
- WeaveScope docker網頁可視化
- lazykube k8s 界面
- Portainer 單機,集群可視化管理
- Rancher 企業級容器編排
- 實例
- redis 單機
- redis 集群
- docker-compose 搭建 lamp 應用
- php實戰項目
- K8S
- 安裝
- 容器可ping 外網 / 給容器局域網 ip
- 遠程使用docker
- 縮小容器體積
- ====== 虛擬化 ======
- ffmpeg 音視頻處理
- 實例
- 查看文件信息
- 轉換編碼格式
- 調整碼率
- 改變分辨率
- 提取音頻
- 截圖
- 裁剪
- 為音頻添加封面
- SRS 流媒體服務器
- ====== 流媒體 ======
- Casbin web訪問權限控制
- Model 與常用配置文件
- 示例
- Hello World
- Http 示例
- gin 示例
- Casdoor 集成登錄
- ====== web 組件 ======
- semgrep 靜態代碼掃描工具
- shellcheck 腳本lints
- ====== Lint ======
- Apollo 強大但部署麻煩
- Nacos 簡單方便
- ====== 配置中心 ======
- 寶塔 面板安裝
- 1Panel 運維管理
- 雷池 站點防護
- ====== Linux 面板 ======
- libreoffice 操作/預覽office
- soffice 命令
- linux 中文字體問題
- 示例
- 預覽 office(word,ppt,xsl) / pdf
- tika 文檔轉文字
- tika-server
- tika-app
- 示例
- http 請求獲取文本內容
- go 與jar 配合
- ====== 文檔 ======
- 禪道
- 快速入門
- ====== 項目管理軟件 ======
- buildroot 交叉編譯
- CGO 交叉編譯實例
- onlyoffice 在線office編輯
- 安裝
- 編譯
- ubuntu16.04 編譯
- 在uos_arm編譯[棄]
- 修改字體
- 示例
- Hello-World
- ebpf 性能追蹤
- Nexus Repository 統一包管理器
- go
- webdav
- chsrc 鏡像自動設置
- 前端
- HTML
- 設計規范
- Web前端兼容性問題
- 手機端
- 尺寸單位
- rem 方案的示例
- JS / jQuery 插件
- 輪播圖 滑動鼠標
- slick 鼠標滑動事件
- swiper 鼠標滑動 案例豐富
- 時間
- Moment 時間解析模塊
- jQuery jquery-date-range-picker 日期區間
- jQuery daterangepicker 日期區間(美觀)
- jquery bootstrap-datetimepicker 日期和時間
- 圖片
- viewerjs 圖片預覽 功能全無需jquery
- grade.js 根據圖片生成背景色
- js-cloudimage-360-view 360度旋轉觀看圖片的 JS 庫
- pagemap 網頁右上角縮略圖
- JQuery jqzoom.js-類似淘寶的圖片放大
- jQuery lightBox-圖片順序預覽
- JQuery Jcrop 圖像裁剪
- X6 圖形繪制工具
- 圖形渲染
- D3
- SnapSVG svg 繪制庫
- pixijs 繪制 WebGL,Canvas
- gojs
- three.js 做3D VR
- css3d-engine 精簡版 treejs
- pano2vr 方便快速的3D-VR
- echarts
- 示例
- 動態時序圖
- smoothie.js 監控圖
- 工具庫
- 下劃線庫 -有兩個庫
- licia 常用開發庫
- Ramda 函數式庫
- API
- 比較運算
- 數學運算
- 邏輯運算
- 字符串
- 函數
- 數組
- 對象
- MOCK
- json-server 偽造 json 接口
- mock.js 隨機數據
- 文件上傳 / 下載
- [推薦]filepond 文件上傳 9.6K start 可編輯圖片
- downloadjs 可讓ie 支持文件下載重命名
- jQuery 多文件上傳進度條 Huploadify
- 單元測試
- mocha 20K
- jest 33.2K
- 匹配器
- cypress 測試
- 視頻播放
- flv.js b站開源
- jessibuca 支持webrtc
- media-chrome 視頻播放器
- ORM
- typeorm
- 實體
- 一對一等處理
- 查找
- 生成器
- 驗證
- 大屏
- 拖拽式 大屏框架
- DataV 基于vue2 大屏
- 加密庫
- CryptoJS
- 網頁編輯器
- monaco-editor 網頁版編輯器
- codemirror
- 移動端相關庫
- better-scroll 更好的滾動
- Pxmu.js 通知,loading 等 [11 star]
- postcss-pxtorem 自動px 轉 rem
- jQuery
- jQuery springy 關系可視化
- jQuery zTree 樹插件
- jQuery select標簽中搜索option
- jQuery jQueryUI
- 拖拽和放置
- 縮放
- 特效
- 滑動選擇
- 排序
- 折疊面板
- 進度條
- 標簽頁
- autocomplete 自動完成
- jQuery form 表單提交插件
- jQuery Validate 驗證
- 使用方式
- 校驗規則
- 實例 validate與 jquery form
- jQuery Cookie
- jQuery Boostrap autocomplete
- jQuery Growl 側邊消息提醒
- jQuery noty 通知
- jQuery Migrate
- Slidev makedown 生成 PPT
- 語法
- makeDown
- Layouts
- theme
- 基礎屬性
- PlantUML
- components
- 對象數據庫
- sql.js 網頁sqlite 數據庫
- 示例
- node 使用
- web 使用
- 獲取遠程庫
- pglite 網頁版 pgsql
- prismjs 語法高亮
- introjs 新手引導
- RequireJS 客戶端模塊管理
- cleave.js 格式化輸入框內容
- fusejs 搜索功能
- tesseract.js 文字識別
- fullPage 全屏滾動網站
- mjml 轉為相應式郵箱html
- progressJs 頭部進度條
- instant.page 鏈接預加載
- pdf.js
- Yjs 協議編輯
- 前端框架
- layui
- 常用方法
- layui.laytpl 前端模板
- 模塊定義
- 常用庫
- form_table
- Cron表達式組件
- notify
- layui-soul-table
- xm-select
- tableTree
- croppers 截圖上傳
- 技巧
- 打開表單
- 表單格式
- layuiAdmin 官方
- LuLu 靈活前端
- ====== 桌面框架 ======
- Frozen UI
- WeChat UI
- MUI 對移動端做了優化
- AUI js 框架
- ====== 移動端 ======
- ficusjs 使用 Web component
- ====== 原生 component ======
- htmlx 無js 頁面交互
- CSS
- 知識
- 最佳網頁寬度
- 產生空白間隙的原因
- 所有元素平滑動畫
- 技巧
- 居中 / 對齊
- 頂端觀看顯示進度條
- 圖片自適應同步的截取
- 元素硬件加速
- 滾動條樣式
- 給列表加豎線
- 文字超出隱藏并顯示省略號
- 打字效果
- 語法
- translate 移動
- transform 轉換
- transition 過渡
- animation 動畫
- ====== 動效 ======
- flex
- grid
- ====== 布局 ======
- 函數
- CSS 變量
- vw,ch 等長度
- box-sizing 屬性
- ====== 技巧 ======
- Font Awesome 字體
- bootstrap v3
- 樣式快速入門
- 基礎樣式
- 布局
- 文本
- 列表
- 表格
- 表單
- 按鈕
- 圖片
- 輔助類
- 關閉按鈕
- 三角符號
- JavaScript 插件
- 模態框
- 標簽頁
- tooltip 提示
- 按鈕 設置加載
- normalize.css 初始化
- animate.css 動效
- tailwindcss css類樣式
- 安裝
- 定制
- 配置 文件
- 組件
- 語法
- container 容器
- Box Sizing
- Display
- 浮動 / 清除浮動
- Object 可控替換元素
- overflow 溢出
- Overscroll 滾動區域邊界時的行為
- position
- Top / Right / Bottom / Left
- visibility 可見性
- Z-Index
- Flex
- Justify Content 控制flex/grid的主軸
- Align Content
- Align Items
- Grid 網格布局
- Justify Items
- 間距
- 內邊距 / 外邊距
- space 控制子元素之間的間隔
- UnoCSS 類似 TailwindCSS
- water.css [7k] 無需class的框架
- simple.css [2.5k] 無需class的框架
- open-props css變量框架
- ====== css 框架 ======
- Sass/Scss與Less區別
- less 不依賴ruby
- z.less 庫- 預定義常用函數
- stylus
- Sass 靠縮進繼承
- scss = Sass 3 靠括號繼承
- ====== css 庫 ======
- jQuery
- 插件
- jQuery 制作插件
- 常用方法
- bind / on / click
- js-ajax-* 實現異步
- 全局body loading 為wj實現
- 根據 event.timeStamp 防抖
- 設置select 的默認值
- 圖片放大
- 圖片懶加載
- 文件異步下載 / 帶百分比
- 文件異步上傳 / 帶百分比
- 拖拽上傳文件
- 常用指令
- AJAX
- 全局 Ajax 事件處理器
- $().ajaxPrefilter ajax前置與后置監聽
- $.get
- $.getJSON
- $.getScript
- $.post
- $.ajax
- $().load
- .serialize() / .serializeArray()
- DOM
- .addClass() / .removeClass()
- .hasClass() / .toggleClass()
- .attr() / .removeAttr()
- .prop() / .removeProp()
- .html() / .val() / .text()
- .data() / .removeData()
- .after() / .before()
- .append() / .appendTo()
- .prepend() / .prependTo()
- .clone()
- .detach() / .empty()
- .each() 遍歷 jQuery 對象
- .get()
- ====== 元素選擇 ======
- .eq() / .first() / .last()
- .filter() / .find() / .has()
- .next() / .prev()
- .parent() / .parents()
- CSS
- .css()
- .height() / .width()
- .innerHeight() / innerWidth()
- .outerHeight() / .outerWidth()
- .position()
- .scrollLeft() / .scrollTop()
- 動畫 / 特效
- .animate()
- .delay() / .finish() / .stop()
- .fadeIn() / .fadeOut() / .fadeTo()
- .hide() / .show() / .toggle()
- .slideDown() / .slideUp() 滑動
- 瀏覽器事件
- .scroll()
- .resize()
- Event 對象
- event.currentTarget
- event.target
- event.data
- event.isDefaultPrevented()
- event.which 按鍵監聽
- event.pageX / event.pageY
- event.preventDefault()
- event.stopPropagation()
- event.timeStamp
- event.result
- event.type
- event.key
- 事件監聽
- .on()
- .one() 觸發一次
- .trigger()
- .off() 移除事件
- 表單事件
- .blur() / .focus()
- .focusin() / .focusout() 支持冒泡
- .change()
- .select()
- .submit()
- 鍵盤事件
- .keydown() / .keypress()
- .keyup()
- 鼠標事件
- .click() / .dblclick()
- .contextmenu() 右鍵
- .hover()
- .mouseup() / .mousedown()
- .mouseenter() / .mouseleave() 鼠標進入 / 移開
- .mousemove() 移動
- .mouseout() / .mouseover() 冒泡移入/移除
- 工具類
- .grep() 過濾數組
- .map() 轉為另一個數組
- .merge() 合并數組
- .each() 遍歷數組和對象
- .inArray()
- ==== 數組 ====
- $.param / $().serialize / $().serializeArray()
- .extend() 合并對象
- ==== 對象 ====
- .trim() 去掉首尾空格
- .parseHTML() / .parseJSON() /.parseXML()
- ==== 字符串 ====
- .isArray()
- .isEmptyObject()
- .isFunction()
- .isNumeric()
- .isPlainObject()
- .type() 可區分 array 與 object
- ==== 類型判斷 ====
- .now() 時間戳
- 函數 compose
- callbacks.add() 添加函數
- callbacks.empty() 清空函數
- callbacks.fire() 調用函數
- JavaScript
- 知識
- 同源限制
- 不同域跨窗口通訊
- typeof / instanceof
- JS 語法樹
- 設計模式
- 嚴格模式
- 性能優化
- scrollHeight 等各中高度
- 技巧 / 場景
- onClickOutside 判斷是否在嚴肅外
- clientX .pageX,screenX,offsetX 區別
- getBoundingClientRect 定位元素
- 下拉示例
- 自定義去除字符
- 打印時間戳
- 類型轉換 黑魔法
- 只初始化一次
- 防抖 / 節流
- 動畫
- ====== 技巧 ======
- this / bind / call /apply
- 函數式編程 / 柯里化
- compose 函數組合
- 原生面向對象寫法
- 示例:canvas小球碰撞
- new 帶prototype的函數
- ES5 實現繼承
- 大文件斷點續傳
- ====== 場景 ======
- 插件
- JS 制作插件
- 實例:拖拽列表插件
- 圖片/文件拖拽顯示信息
- js 原生提示
- 手寫簽名
- JS 模塊
- ES6 [推薦]
- CommonJS 模塊
- ES6,7,8語法
- Promise
- Class
- Map / Set
- async / await
- 瀏覽器對象
- 瀏覽器環境概述
- window 對象
- Location 對象
- Navigator 對象
- Screen 對象
- XMLHttpRequest 異步請求
- console 對象
- URL 解析
- URL 的編碼和解碼
- URLSearchParams 對象轉url參數
- 標準庫 / 對象
- Object 對象
- Number 對象
- Array 數組
- String 對象
- Math 對象
- Date 對象
- RegExp 對象
- JSON 對象
- FormData 對象
- ArrayBuffer / Blob 對象
- File / FileList / FileReader 對象
- TextEncoder / TextDecoder
- DOM
- DOM,Node 接口
- Document 節點
- Element 等節點
- CSS 操作
- 事件
- EventTarget 事件通用接口
- Event 對象
- 鼠標事件
- 鍵盤事件
- 進度事件 - 加載外部資源
- 觸摸
- 實例 手寫
- PointerEvents 更通用的touch
- 拖拉事件
- 窗口事件
- 剪貼板事件
- GlobalEventHandlers 接口
- HTML 標簽
- <a>
- <img>
- <input> 元素
- Web Api
- Fetch
- Response 對象
- Request 對象
- Headers 對象
- 實例
- POST 請求
- JSON 請求
- 上傳文件
- 獲取數據流-如圖片
- 逐行處理文本文件
- 自定義請求 Request
- sessionStorage / localStorage
- Intersection Observer 元素可見判斷
- PerformanceObserver 性能監聽
- ResizeObserver 監聽元素大小
- TextDecoder / TextEncoder
- Gamepad 游戲手柄
- geolocation 地理位置
- 網頁可見性 狀態監聽
- Notification 系統通知
- 畫中畫API
- Pointer events 指針事件
- Vibration API 震動
- Audio API 聲音
- Web Share API
- WebCodecs API 幀和音頻塊的訪問
- Mutation Observer 監視 DOM 變動
- 數據類型
- TypeScript
- 技巧
- 聲明文件
- 全局變量
- npm 包中使用
- UMD 庫
- 模塊插件
- tsconfig.json
- 語法
- 基礎類型
- 裝飾器(decorators)
- 命名空間
- 模塊
- 高級類型
- 類型兼容性
- 接口
- 類
- 函數
- 泛型
- Record
- 高級類型
- ====== 基礎 ======
- SVG
- 語法
- js 操作 SVG
- canvas
- 繪制矩形
- 繪制路徑
- 繪制直線
- 繪制圓弧
- 繪制貝塞爾曲線
- 繪制文本
- 繪制圖片
- 樣式與顏色
- 狀態的保存和恢復
- 變形
- 平移
- 旋轉
- 變形矩陣
- 合成
- 裁剪路徑
- 動畫
- WebSocket
- 庫
- websocketd
- socket.io
- WebGL
- twgljs 輕量級庫
- WebRTC
- WebRTC 使用流程
- 概念
- 處理瀏覽器中的媒體
- 兩種傳輸方式示例 視頻 / 文本 / 流文本
- 需要信令通道
- 教程
- 媒體設備
- 對等連接入門
- 遠程流
- 數據通道
- TURN服務器
- API 接口
- RTCPeerConnection
- getUserMedia
- 示例
- examples
- php 實現服務器與web端
- 捕獲窗口
- 捕獲攝像頭
- 本地使用 RTCPeerConnection
- DataChannel
- 遠程點對點
- 第三方庫
- SimpleWebRTC [4.5k]
- webRTC.io [1.6k]
- ==== 視頻聊天 ====
- peerjs 點對點鏈接
- 點對點傳輸文字
- 第三方項目
- p2p.chat
- im
- WebAssembly
- 示例
- hello-world go版
- SSE (EventSource)
- 示例
- Web Workers 多線程
- 示例
- 通用的異步 eval()
- Service Worker API
- PWA 提升WebApp
- Broadcast Channel 廣播
- IndexedDB
- 庫
- Dexie.js 封裝 IndexedDb
- ZangoDB
- JsStore 帶SQL語法
- lovefield 仿 SQL [6.8k]
- ====== 進階 ======
- NodejS
- npm 插件
- mongoose 操作 mongodb
- sequelize 數據庫orm
- pm2 啟動 node
- nodemon 監控文件變化自動重啟
- cookie-parser 設置 cookie
- Puppeteer 控制瀏覽器
- Robotjs 桌面自動化
- anyproxy 代理
- pkg 編譯成二進制
- 文件操作
- 網絡操作
- 進程管理
- Express 框架
- 模塊化編程
- Koa web 框架
- Deno 代替node
- bun
- 命令
- bunfig.toml
- 接口
- API
- Bun APIs
- Web APIs
- Node Js
- ====== 后端 ======
- Vue
- 問題
- 運行網頁,但是報缺少 Node 的相關庫
- 技巧
- 異步加載
- 動畫,與動畫庫的使用
- webpack 構建多頁面
- vue3.0 語法
- reactive,ref,watch,watchEffect,computed
- 子組件
- TypeScript
- 性能優化
- 測試 Vitest
- 動畫
- 依賴注入 Provide與Inject
- Suspense 異步加載組件
- directives 自定義指令
- 組合式函數 useXXX
- 插件
- vue 庫
- axios 請求
- vue cli 3.0 配置
- qrcode.vue 二維碼
- Vue-router
- vue-i18n
- VeeValidate
- vueuse
- 存儲 useLocalStorage 等
- ref 的 各種undo,redo
- ====== State ======
- useActiveElement
- useDraggable
- useDropZone 可拖動到區域
- useElementBounding
- useElementSize width,height
- 元素可見性
- useMouseInElement
- useWindowScroll
- useWindowSize
- useTextareaAutosize 自動增高
- useTitle
- useUrlSearchParams url參數
- onClickOutside 元素外點擊
- useFocus / useFocusWithin 元素是否激活
- ====== Elements ======
- useClipboard
- ColorMode 切換主題
- useEventListener
- useFileSystemAccess 文件信息
- useObjectUrl 查看文件內容
- useFullscreen
- useMediaControls 媒體內容
- usePermission 權限
- useWebNotification
- useWebWorker
- ====== Browser ======
- onKeyStroke 監聽鍵盤
- onLongPress 長按時長
- useDevicesList 媒體設備
- useDisplayMedia 使用設備源
- useGeolocation 定位
- useInfiniteScroll 下拉滾動
- useKeyModifier 按鍵監聽
- useMouse
- useNavigatorLanguage 語言
- useNetwork
- usePageLeave
- useSpeechRecognition 語音
- useTextSelection 選中文字
- ====== Sensors ======
- ====== Component ======
- useVirtualList 虛擬列表,高性能
- ======== 工具庫 ========
- watchDeep 監聽深度對象
- watchDebounced 防抖
- watchOnce 監聽一次
- watchThrottled 節流
- useDebounceFn /useThrottleFn 防抖函數
- useEventBus 通知
- ====== watch ======
- useArrayDifference
- ====== Array ======
- useDateFormat 當前時間
- useTimeAgo 多久前
- ====== time ======
- useAsyncValidator 驗證
- useChangeCase 單詞切換
- useCookies
- useQRCode 二維碼
- useSortable 拖拽排序
- ====== Integrations ======
- ====== 工具庫 ======
- better-scroll 更好的無滾動條插件
- vue-infinite-scroll 下拉加載
- vue-infinite-loading 上拉刷新,功能強
- vue-lazyload 圖片懶加載 -vue2.0
- Vue.Draggable 拖住div
- vue-fullpage
- form-generator 表單生成器[UI版]
- vue-form-making element-ui 可視化表單
- vue-cron Cron表達式組件
- vue-good-table 表單組件
- vxe-table
- skeletonreact 骨架屏
- ======== UI 庫 ========
- vuex 狀態管理
- 在多頁面中使用
- 創建 store.js
- Pinia 狀態管理
- pinia-plugin-persist-uni 適配 uni
- hello world 實例
- ======== 狀態庫 ========
- Nuxt 集成服務器渲染,ui框架等
- vue-element-admin
- ant-design
- d2-admin vue+ElementUI 后臺框架
- vuetifyjs 37.4k
- 特性
- 別名
- 全局配置
- 字體圖標
- i18n
- scss
- 主題
- 輔助類
- 組件
- v-spacer 空白彈框
- v-item-group
- v-hover 懸停事件
- v-list
- 指令
- v-ripple
- v-scroll
- ======== 框架 ========
- React
- 第三方庫
- ChatUI
- wasp 快速制作前后端
- motion.dev 動畫庫
- zustand 狀態管理
- immer 優雅更新state對象
- Shadcn UI 可定制UI 框架
- lucide-react 圖標庫
- swr 請求庫
- react-query 請求庫
- date-fns 時間
- zod 驗證
- react-hook-form
- react-hot-toast 通知9.9k
- 語法
- hook
- 自定義 hook
- useEffect
- useMemo 緩存計算結果
- useSyncExternalStore 獲取外部數據
- useCallback
- useDeferredValue
- 組件
- StrictMode 嚴格模式
- Suspense 加載前的提示
- API
- 組合 vs 繼承
- 狀態提升
- 表單
- 列表 & Key
- 條件渲染
- 事件處理
- State
- 組件 & Props
- JSX
- Context 深層傳遞參數
- ref 更新不觸發刷新
- Next.js
- Routing
- pages
- layout
- Routing
- Error Page
- Loading
- Link
- Parallel Routes
- Intercepting Routes 模彈窗路由
- layou 布局
- 環境變量
- API 路由
- Svelte
- 示例
- 編譯為一個web Component
- Web Components
- 示例
- template 方式
- javascript 方式
- 鴻蒙
- 安裝
- 示例
- Hello World
- 目錄說明
- resources 目錄
- ArkTS 語言
- 組件
- 狀態管理
- LocalStorage 頁面級狀態
- AppStorage 全局狀態
- emitter 事件監聽
- PersistentStorage 持久化
- Environment
- ASK UI 框架
- 布局
- 組件
- ====== 框架 ======
- React Native
- 基礎知識
- Electron 桌面應用
- 快速入門
- 技巧
- 內置模塊
- app 模塊
- BrowserWindow
- Menu 菜單
- globalShortcut (全局快捷鍵)
- Shell
- dialog 對話框
- tray 系統托盤
- webContents 渲染以及控制 web 頁面
- ipcMain / ipcRenderer (進程間的通訊)
- clipboard 剪切板
- webview
- protocol 自定義協議
- desktopCapturer 獲取其他軟件信息
- 常用包
- electron-settings 設置管理器
- electron-log
- electron-builder 打包[推薦]
- electron-packager 打包
- electron-updater 升級
- electron-store 以文件形式緩存配置
- menubar 托盤菜單欄
- photon 桌面 UI 構建
- React Desktop macOS和Windows的UI工具包
- chrome-tabs
- xel 界面ui
- electron-util 常用包
- electronic-vue
- wails go實現的跨平臺
- Runtime
- Events
- Log
- window 窗口
- Dialog 對話框
- Menu 菜單
- Browser 瀏覽器
- Clipboard 剪貼板
- Screen
- app 參數
- tauri 桌面開發
- 系統APi
- weex 跨平臺vue 開發
- weex-ui 第三方 ui 庫
- wexx-bindingx 動畫效果
- wails go版pc端
- Taro 小程序
- 技巧
- 配置
- 路由
- 編譯優化
- NutUI UI組件
- subPackages 分包
- 組件庫
- CustomWrapper 用于動態更新
- PageContainer 半屏頁面
- RootPortal 彈窗
- ScrollView 滾動
- Swiper/SwiperItem
- Vue
- 生成周期
- NutUI 基于vueUI庫
- uniapp
- 插件 / 資源
- [通用] 更好的下拉刷新,上拉加載
- [app] 全量更新 app-簡單
- [app] 可增量更新
- 登錄/注冊模板(含微信等第三方登錄)
- 導航欄
- uni-form 表單校驗
- combox 自動完成
- uni-data-checkbox
- uni-data-picker
- uni-loadmore 上拉加載更多
- uni-row 布局
- uni-dateformat 日期格式化,倒計時
- uni-file-picker 文件上傳
- uni-search-bar 搜索欄
- uni-segmented-control 分段器
- UI 框架
- uni-框架
- ColorUI-UniApp
- uView UI 更多功能
- 快速入門
- 設計圖尺寸
- 設置開發/生產模式
- 設置 scss 等樣式
- 生命周期
- 組件/標簽的變化
- template 與 block
- NPM支持
- 資源路徑
- css 相關
- js 導出模塊
- 使用 TypeScript
- 組件管理
- 事件處理器
- vuex
- 配置
- pages.json
- easycom
- package.json
- uni.scss
- App.vue
- main.js
- 生命周期
- 應用生命周期
- 頁面生命周期
- 組件生命周期
- Vue
- 事件處理器
- 表單使用 v-model
- 組件的props
- 組件的ref
- 組件的.sync 子組件prop通知父組件
- 原生組件
- button
- page-meta
- navigation-bar
- custom-tab-bar
- open-data
- 運營服務
- 統一推送uniPush
- 運營統計
- 制作統一發行頁面
- API
- 媒體
- uni.compressImage 壓縮圖片
- 設備
- 陀螺儀
- 系統信息
- 網絡狀態
- 羅盤
- 加速度計
- 撥打電話
- 掃碼
- 剪貼板
- 屏幕亮度
- 手機振動
- 藍牙
- 生物認證
- 鍵盤
- 界面
- 彈出菜單
- 設置導航條
- 設置 tabBar
- 背景/下拉背景
- 動畫
- 滾動頁面
- 網絡字體
- 下拉刷新
- 節點信息
- 節點布局相交狀態
- 文件
- 繪畫
- 第三方服務
- 獲取服務供應商
- 登錄
- 檢測是否登錄
- 微信登錄
- 信息獲取
- 獲取手機號
- 手機號一鍵登錄
- 支付
- 推送
- 模板消息-小程序
- 授權
- 小程序設置界面
- 收貨地址
- 打開其他小程序
- 模版消息
- 訂閱消息
- 小程序更新
- App 更新
- 調試
- 統計 - uni 對程序的統計
- 廣告
- 頁面通訊 / 全局事件監聽
- 公用模塊 / 全局變量
- uni_modules
- datacom
- 自動化測試
- wexx / nvue
- HTML5+
- 國際化
- 微信小程序
- ====== 平臺相關 ======
- webpack
- loader 插件
- babel-loader ES6 轉為 ES5等
- html-loader
- css-loader
- postcss-loader 對 css 進行后處理
- less-loader
- url-loader 過小生成 base64位圖片
- file-loader 引入圖片
- image-webpack-loader 圖片壓縮
- 引入模塊-并對模板賦值
- esbuild
- Api
- Build API
- 高級配置
- 語法
- gulpjs 構建工具
- 快速入門
- 語法
- 常用插件
- css 插件
- js 插件
- 圖片 插件
- 自動刷新頁面
- 示例
- 編譯sass
- 監聽 css變化
- 監聽 文件變化,刷新頁面
- 多頁面示例
- 模版
- rollup 0配置打包腳本
- Rspack 基于Rust,兼容webpack
- lerna 管理包含多個軟件包
- 命令
- 快速入門
- vite
- 功能
- 命令行
- vite
- 插件
- 兼容傳統瀏覽器插件
- 示例
- 普通 html, 支持 import
- ====== 構建工具 ======
- npm
- npm 插件制作發布
- cnpm - 淘寶的 npm 鏡像
- npx
- yarn
- 命令
- plugin
- .yarnrc.yml
- pnpm
- 命令選項
- Bower 瀏覽器管理插件
- ====== 包管理 ======
- SEO 優化
- ====== 性能與優化 ======
- vConsole
- 遠程調試移動設備網頁
- chil 遠程調試網頁
- 遠程調試 Android 設備網頁
- selenium 自動測試
- selenium IDE
- selenium Python
- 常用技巧
- 定位 元素 / 一組元素
- 控制瀏覽器操作
- WebDriver常用方法
- 鼠標事件
- 鍵盤事件
- 獲取斷言信息
- 設置元素等待 -等待某條件成立后在執行
- 多表單切換
- 多窗口切換
- 警告框處理
- 下拉框選擇
- 文件上傳
- cookie操作
- 調用JavaScript代碼
- 窗口截圖
- 關閉瀏覽器
- Chrome headless 無界面模式
- CukeTest 可測桌面應用
- 語法
- Tree 結構的選擇
- 數據驅動測試用例
- 模型管理器
- 批量運行工具
- 常用工具函數
- Cucumber API
- this.attach 在執行后進行截圖
- 每個場景后截圖至報告
- 模擬桌面操作API
- 模擬 Ctrl+A
- 禁用中文輸入法
- ====== 使用工具 ======
- 谷歌瀏覽器插件
- 概念
- manifest.json
- popup
- background
- content
- plasmo 瀏覽器插件框架
- 示例
- Popup
- options 選項頁
- newtab 新標簽
- background
- messaging 通信
- content
- Tab pages
- storage
- Env
- package 轉 manifest
- Assets
- Icon
- lang
- 谷歌接口
- extension
- browserAction
- tabs
- contextMenus
- notifications
- omnibox
- 互相通信概覽
- 長連接和短連接
- windows
- storage
- webRequest
- cookies
- runtime 插件相關
- manifest
- ====== 瀏覽器插件======
- chrome
- puppeteer js控制chrome
- DevTools protocol 通過websocket控制
- 命令行
- go 版本
- ====== chrome 控制 ======
- XPath
- ====== 文本生成圖 ======
- plantuml
- mermaid.js
- 軟件
- jetbrains / Intellij IDEA
- 常用插件
- Git Commit Message Helper
- Chinese ?(Simplified)? 中文組件
- Php Inspections ?(EA Extended)
- redis simple -redis 客戶端
- plantuml-integration uml 繪制
- 制作插件
- 連接遠程docker
- 配置vagrant虛擬機
- 保存監聽 eslint
- uni-app 代碼提示
- docker 使用 phpstorm/php-71-apache-xdebug
- php 本地debug / 遠程debug
- php 代碼檢測
- grumphp 限制 commit 提交
- vs code
- C++ 配置
- Go 配置
- Qt 配置
- 插件
- 單元測試
- i10n
- 發布插件
- 擴展工作臺
- 數據儲存
- package.json 清單
- visual studio
- 使用 Clang/LLVM
- 運行Qt
- 內網部署vs及插件
- 插件
- ReSharper C++
- Clang Power Tools
- Sublime Text配置
- github
- gource 通過 git 生成 動畫
- thefuck 出現錯誤使用 fuck
- tldr 簡化 man 函數
- postman
- Apache JMeter 并發測試工具
- Chrome
- 控制臺
- Apche Directory Studio - LDAP軟件
- sokit 端口監聽 轉發. socket 測試工具
- wireshark 抓包工具
- Ventoy 多系統合一啟動盤制作工具
- UserLAnd 手機安裝linux
- termux 手機安裝 linux
- sharemouse 跨系統操作
- Microsoft Garage Mouse 多windows跨鍵盤
- syncthing 分布式同步
- D盾
- openArk
- 搭建 shandowsocks
- google云 搭建
- 亞馬遜云 搭建
- 終端走代理
- 一鍵 ss 腳本
- ????? 無界面軟件 ??????
- sqlmap 防sql 注入的測試
- scrcpy 手機投屏
- sftpgo 跨平臺 ftp
- frp 內網穿透
- AWS 亞馬遜
- 小米路由AX3600
- upx 壓縮可執行文件
- firebase 賽博菩薩軟件
- 安卓
- adb
- emulator 虛擬器
- 安卓抓包
- MAC
- php 環境配置 2.0版
- pear / pecl 安裝
- Mac 配置 Python 和Python3
- 配置 Oh My Zsh+ iTerm2
- iTerm2 自動登陸 ssh
- 配置 Vim
- brew
- 創建 brew 包
- MAME 街機模擬器
- php-osx mac 安裝php
- 破解 wifi
- iOS注冊美區Apple ID教程
- Window
- 常見問題
- 打不開微軟商店
- cmd 命令
- cmd 運用場景
- 復制目錄
- 刪除目錄下的所有文件
- < 交互時可自動輸入
- 查看端口占用的pid
- 當前目錄管理員身份運行
- 批處理命令
- echo / rem 注釋
- pause 暫停
- call 調用其他 bat
- goto
- set 設置變量
- 獲取命令行參數
- 常用命令
- tasklist 查看進程
- taskkill 進程操作
- ipconfig
- nslookup 域名解析
- netstat
- route 路由信息
- arp 查看ip使用情況
- findstr
- robocopy
- SpaceSniffer 檢查磁盤文件暫用大小
- choco win包管理神器
- 創建 choco 包
- 實例
- nupkg 常用函數
- WSL 2 -方便win docker
- Sysinternals 微軟工具箱
- Autologon 免密登錄
- Psexec 遠程執行工具
- Autoruns 查看啟動項
- AdExplorer / AdInsight AD與LDAP查看器
- BgInfo 電腦信息生成到桌面
- LogonSessions 列出登錄時間
- PsInfo 系統信息
- PsKill 終止(本地或遠程)進程
- PsPing Tcp ping
- PsLoggedOn 顯示登錄的用戶
- PsPasswd 更改本地或遠程的密碼
- PsShutdown 關閉或重啟(本地或遠程)電腦
- RDCMan 批量管理遠程
- TcpView 列出套接字
- ZoomIt 屏幕縮放
- scoop 包管理器
- 添加ftp 服務
- vcpkg c++包管理器
- 升級 TLS
- clumsy 模擬不穩定網絡環境
- Dependencies 查看 exe 依賴的dll
- portableapps 軟件裝U盤
- mobaXterm 類Xshell
- mouse without borders 共享鍵鼠
- IIS
- dumpbin 類似 linux 的 ldd
- Linux
- 知識碎片
- profile 與 bashrc
- /etc/init.d/functions 公共函數
- 實例
- &>file、2>&1、1>&2、/dev/null
- 管道和重定向
- 守護進程腳本
- 幾個重要的信號
- cli a-z 常用命令注解
- 選項優先級
- 使用場景
- 創建用戶,給root權限
- 設置服務器時間
- [自制] 批量操作多節點的腳本
- 引用環境變量替換文字模版
- umount 掛載硬盤
- 內核版本/系統版本信息
- 設置靜態 IP
- 常用命令
- 文本 / 文件 / 目錄
- egrep = grep -E 查看文件內容
- grep 查看文件內容
- awk 對文本每行處理
- sed 處理文本文件
- xargs 多行轉換
- find 文件查找
- locate 比find 更快的索引
- wc 統計文字
- tr 替換與清除
- cut 按列切分
- tee
- 守護進程
- systemd 定時器
- systemctl 守護進程
- systemctl
- Unit.server 配置
- 實例
- 講解 sshd 配置
- 實例 配置 go-web
- Type=forking 的使用
- journalctl 日志管理
- systemd-analyze 啟動耗時
- hostnamectl 主機信息
- localectl 查看本地化設置
- timedatectl 查看當前時區設置
- loginctl 查看用戶信息
- goreman 服務管理 [神器][golang]
- supervisor [python]
- supervisord [golang][帶GUI]
- chkconfig 開啟啟動管理
- 標準 init.d 模版
- httpd 開啟啟動
- 調試工具
- strace 調試腳本
- pstack 跟蹤進程棧
- perf 性能分析工具
- stress 壓力測試
- ab 壓測工具
- ldd 查看執行文件的依賴
- readelf 動態庫的真實版本
- patchelf 強制指定LB_LIBRARY_PATH
- tcpdump
- gdb 調試利器
- lsof 查看當前系統文件
- ss 網絡端口查詢
- free 內存情況
- iotop 查看進程 IO
- iftop 網絡 IO 監控
- tc 模擬弱網
- 運維工具
- ansible 批量執行多服務器
- awx UI管理工具
- expect - 自動交互腳本
- envsubst 替換模版中的環境變量
- top / uptime
- sshpass 非交互密碼登錄
- bash-completion 命令補全
- 查看硬件信息
- lscpu 顯示cpu型號
- arch 查看架構
- uname 查看系統版本
- cat /proc/meminfo 查看內存信息
- lsb_release 系統信息
- arch cpu架構
- ulimit
- 網絡工具
- nmcli 配置靜態網絡
- nmap 端口掃描
- 磁盤管理
- df 磁盤使用情況
- du 統計文件占用
- 管理用戶/組
- useradd
- usermod
- userdel
- groups 查看
- groupadd
- groupmod
- groupdel
- passwd
- openssh
- ssh openssh-client包
- 客戶端配置文件
- sshd openssh-server包
- openssl 使用 openssl 包
- 實例
- 服務器證書 .key 與 .pem
- 客戶端證書
- 同時生成服務端與客戶端證書
- 登錄方式
- ssh-keygen 秘鑰登錄
- ssh-agent / ssh-add 秘鑰記住密碼
- 證書登錄
- 端口轉發
- scp
- rsync 增量同步
- sftp
- gcc
- 靜態庫
- 動態庫(共享庫)
- 安全
- firewall-cmd 防火墻
- iptables
- asd 內存硬盤
- ln
- tar
- diff
- watch
- patch
- Curl
- wget
- Vim
- Tmux
- NFS 文件共享
- ftp
- logrotate linux 日志切割
- NFS 網絡文件
- manpages-zh 中文man
- Bash 腳本
- 快速入門
- 知識點
- $()與反引號區別
- 檢查返回值
- !$ / !*
- shell替換上一條命名的變量
- bash 最簡單 kv 數據庫
- echo / printf / 快捷鍵
- Bash 的模式擴展
- 引號和轉義
- 變量
- 常見變量
- 字符串操作
- 算術運算
- 參數
- getopts Bash內置
- getopt 基本也自帶
- env / shift / exit
- read 用戶輸入值
- 條件判斷
- select 菜單選擇
- 循環
- 數組循環
- 花括號迭代
- seq 設置起始增量
- 函數
- 數組
- set 命令
- 腳本調用堆棧
- mktemp 命令,trap 命令
- Bash 啟動環境
- 命令提示符
- 顏色
- 第三方腳本
- trash.sh 刪除進回車站
- centos 7
- 安裝 gui
- yum
- 切換 yum 源
- 建立 yum 倉庫
- rpm
- .src.rpm 包含源碼的rpm包
- rpm2cpio 只獲取 rpm 包內文件
- rpmbuild 制作 rpm 包
- rpmbuid 命令
- 布局說明
- 變量說明
- macros rpmbuild 宏文件
- Group 分組
- 實例
- 通用模版
- nginx 實例
- 注冊為 systemctl 服務
- 一個同時匹配 rpm 與deb 的腳本
- 支持 jenkins
- ubuntu
- 安裝圖形化
- 美化界面
- apt
- dpkg
- 制作 deb 包
- UOS
- 數據庫
- 知識
- CTE 創建SQL變量
- 自聯結
- 臨時函數
- over 窗口函數
- mysql / sqlServer / oracle 共性
- 創建一個大量表的sql
- 開源庫
- readyset 自動緩存
- ODBC
- Centos 安裝 ODBC
- Windows 安裝 ODBC
- Mysql / MariaDB
- 安裝
- windows
- linux 編譯安裝
- 精簡大小
- mariadb-win-my.ini 配置文件
- 場景
- 數據庫遠程登錄
- 打印全部日志
- 開啟慢查詢
- 清除/關閉 查詢緩存
- 查看 cpu 占用過高
- 取消嚴格模式
- 修改/忘記 密碼
- 主從復制
- 服務無法啟動
- mysql 分區
- 備份還原
- 基于 時間/位置 恢復
- 完整的 mysqldump 備份與恢復示例
- crontab定時備份腳本
- 新賬號設置只讀權限
- 技巧
- 查看性能情況
- sql 技巧
- my.cnf 文件讀取優先級
- conf 文件優先級
- MySQL 函數
- 運算符
- 字符串函數
- 數字函數
- 日期函數
- 高級函數
- 可執行命令
- Mariabackup 熱備份工具
- mysqlslap 性能測試工具
- mysqladmin
- mysqlcheck 修復/優化/分析表
- mysqld_safe
- mysqldump
- mysqlbinlog 操作記錄
- 第三方庫
- soar sql檢查
- soar-web web-ui 版本
- vitess 集群化
- 字段類型說明
- kingshard mysql 代理選擇使用主或從執行 sql
- PostgreSQL
- 安裝
- 場景
- 問題
- 重置密碼
- 批量mock數據
- 命令行
- psql
- pg_dump / pg_dumpall
- pg_restore
- pgbench
- createuser 創建用戶
- 技巧
- USING 關聯表
- 查看表結構
- 物化視圖(讀多寫少緩存)
- Notify-Listen
- 語法
- 數據類型
- 數值類型
- 數組類型
- JSON 類型
- HSTORE 鍵值對存儲
- 枚舉類型
- 組合類型
- 范圍類型
- tsvector 文本搜索類型
- 函數和操作符
- php 原生中文分詞
- 外部數據源
- mysql 數據源
- mongo數據源
- 文件源監控
- redis_fdw
- file_fdw
- 增刪改查
- 表操作
- 模式操作
- 表繼承
- WITH 查詢
- 樹結構表
- 分表
- CHECK 檢查約束
- 域類型
- 圖數據庫
- 索引類型
- 數據庫操作
- EXPLAIN
- 高可用
- 插件
- pglogical 訂閱發布-邏輯復制
- 訂閱發布
- PostGIS 幾何空間,地理
- TimescaleDB 時序
- pg_stat_statements
- pgcrypto
- pg_trgm 索引前后模糊查找
- Citus 水平擴展
- uuid-ossp
- pg_jieba 中文分詞
- pgpool-II 主從和負債均衡和緩存
- 三方庫
- postgrest
- 配置文件
- RESET API 參數
- 客戶端封裝請求
- preset go實現
- pgx go驅動
- ParadeDB 可媲美 Elasticsearch
- pg_partman 自動分區
- pg_cron定時任務
- Pigsty 運維和監控
- Oracle
- pkg-config 安裝
- SQL Server
- sqlite
- 語法
- 數據類型
- 擴展
- FTS5 全文索引
- 內存數據庫
- JSON 處理
- R-Tree 地理位置
- WebAssembly 版
- 庫
- 示例
- rqlited 分布式sqlite
- ==== 關系型數據庫 ====
- TiDB mysql 協議 可分布式
- CockroachDB postgresql 協議
- go-實例
- FerretDB -MongoDB協議,go 實現
- ==== golang 實現====
- MemSQL
- 示例
- go
- VoltDB
- 示例
- golang
- ==== 內存關系型數據庫 ====
- 金倉數據庫 仿Pgsql
- 安裝
- 技巧
- 配置 odbc
- 問題
- SQL 語法
- 調用
- goalng 調用
- php 調用
- 達夢數據庫 仿oracle
- sql 語法
- php 注意事項
- pdo thinkphp6 遷移工具適配器
- OceanBase 阿里
- ==== 國產化數據庫 ====
- clickhouse
- Hbase
- ==== 列數據庫 ====
- MongoDB
- 技巧
- 打開慢查詢
- 場景
- 刪除對象數組中的某條記錄
- 用戶認證
- 索引 設置過期索引 / 全文檢索
- 自增id
- 數據庫/表操作
- 原子操作
- 固定集合 | 用于存放日志
- 多表關系
- 分片(分布式集群)
- 3.x 版本
- 4.2 版本 [ 4.0集群切片增加不會轉義數據 ]
- 搭建集群
- 刪除切片
- 設置 Balancer 運行時間
- 以文件方式啟動,推薦配置
- mongo分片集群添加登錄認證
- 數據備份
- GridFS 文件存儲
- golang 操作 mongo
- MapReduce 統計
- Redis
- 字符串 / 列表 / Hash / Set / Zet / 基數統計算法
- 隊列 /訂閱發布 php實例
- 事務 / bitmap 位圖 / 地理位置
- 管道 / 分布式鎖
- 備份與恢復 / 性能測試
- 設置密碼 / 模糊查詢
- 性能優化
- 監聽過期 key
- docker 集群
- php 連接集群
- 單機測試集群 (官方一鍵安裝)
- 生成環境 官方集群
- Codis 分布式 Redis 解決方案
- 主從模式 / 哨兵模式
- Memcached
- LevelDB kv 存儲 google開源
- golang 示例
- dragonfly 內存型,兼容Redis與Memcached
- RethinkDB
- ==== 非關系型數據庫 ====
- influxdb 數據庫(用于日志存儲)
- ==== 時序數據庫 ====
- neo4j
- 安裝
- Cypher查詢語言
- 示例
- go
- ==== 圖形數據庫 ====
- zincsearch 輕量級全文搜索引擎 [go實現]
- 索引
- 數據
- 搜索
- Elasticsearch 全文搜索引擎
- index(索引)操作
- type(表)操作
- ElasticHD 可視化 docke 安裝
- elasticsearch-head 可視化
- 集群部署
- 支持 php
- 增刪改查
- 封裝成 mdel
- gofound- go 實現的全文索引
- sphinx
- 示例
- 快速入門
- ==== 輕量級全文搜索引擎 ====
- undb 網頁數據-帶RESTAPI
- 消息隊列
- RabbitMQ
- Direct 直發模式 php 版
- Fanout 分發模式 php 版
- Topic 模糊模式 php 版
- Zeromq
- go-zmq4 使用教程
- NSQ [2.7k] go實現的,部署簡單
- nats
- Kafka
- 分布式對象存儲
- minio 分布式對象存儲
- 將MySQL / MongoDB 等 備份存儲到MinIO Server
- 通過 nginx 代理 調用 monio
- hadoop 分布式 分布式存儲
- 偽分布式版
- 集群版
- go 調用
- Hadoop Shell命令
- WebHDFS REST API (使用curl)
- JuiceFS 分布式文件存儲
- 安裝
- 示例
- SQLite 和阿里云 OSS 對象
- 服務發現
- Consul [21.9K]
- 安裝
- etcd [35.6k]
- 命令
- etcdctl
- 示例
- go 操作 etcd
- go 服務發現實現
- 搭建etcd集群
- 搭建單機集群
- 架構設計
- 軟件架構
- DDD分層
- Go示例
- 分層架構
- 事件驅動架構
- 微核架構(插件架構)
- 微服務架構
- 微服務三劍客
- 熔斷
- 限流
- 負載均衡
- API 網關
- 云架構 - 最容易擴展的架構
- 數據庫設計
- dept_code 具有層級關系的子層級
- 數據庫規范
- slq 優化
- 索引失效的場景
- 認證
- 開放平臺認證
- 雙因素認證
- APP 的 token 認證
- JWT - JSON Web Token 驗證
- OAuth 2.0
- HTTP 接口設計
- 簽名設計
- Go 簽名驗證
- PHP 簽名驗證
- 冪等性設計
- 接口限流
- 原子計數器
- 漏桶算法
- 令牌桶算法-常用
- 網關層限流
- RPC
- json-rpc_2.0 規范
- HTTPS 升級指南
- 快速入門
- Let's Encrypt 免費證書
- RESTful 規范
- 設計API
- 常用狀態碼
- 緩存
- 壓縮
- 安全
- API版本控制
- 內容協商
- application/vnd.api+json 響應格式(太啰嗦,不推薦)
- JAX-RS 2.0 [Java API]
- API文檔
- apidoc [8.6k]生成文檔
- showdoc [7.8k]技術文檔、API 文檔
- swagger
- OpenAPI
- go-swagger
- meta
- route
- parameters
- response
- model
- 示例
- swag go的實現
- hello world
- gin 集成
- 文檔/手冊
- docsify 運行時解析
- dumi 為組件開發
- starlight astro
- yaml / toml 等配置文件
- yaml 配置文件用法
- toml
- 持續集成
- 概念
- Jenkins 和 Gitlab 交互
- README 規范
- 徽章
- 代理
- Connect 代理
- 分布式系統
- 分布式 ID 生成器
- 雪花算法
- UUID
- NanoID
- 分布式鎖
- 延時(定時)任務系統
- 分布式搜索引擎
- 負載均衡
- 分布式配置管理
- 分布式爬蟲
- 分布式事務管理器
- 加密
- PGP
- GPG 命令
- 示例
- 生成 pgp 證書
- golang 示例
- monorepos 多子模塊管理
- 相關工具
- 管理最佳實踐
- 發布方式
- 服務器分批
- 業務分批
- 通用代碼技巧
- 日志平臺設計
- ELK 組合
- PaaS架構教程
- 郵箱協議
- 軟件開發模式
- 敏捷開發
- 自動生成更新日志
- git-chglog 2.7k
- git-cliff 9.1k
- 設計決策原因 ADRs
- 概念
- 系統
- 進程
- Poll 與 Epoll
- 文件描述符
- 管道符
- 進程與線程的區別
- 進程狀態
- 死鎖 / 活鎖
- 文件鎖
- 孤兒進程 / 僵尸進程
- 進程間通信
- 共享內存
- Cgroups 資源隔離-docker基礎
- Namespaces 資源隔離
- 內存堆棧
- POSIX
- umask 文件創建掩碼
- sendfile 優化文件傳輸
- 加密
- 證書相關(如:ssl,pem 等)
- 網絡
- HTTP
- 狀態碼
- 請求方法
- 響應頭信息
- http緩存相關
- IP / 子網掩碼 / 網關
- 大端序/小端序
- cookie-http-only
- 靜態網站
- hugo 48.4K 靜態網頁
- hexo 31.7K 創建博客
- 開源協議說明
- 正則
- IP 說明
- 0.0.0.0
- 255.255.255.255 廣播
- 127.0.0.1
- 224.0.0.1 組播(多播)
- golang 示例
- 169.254.x.x
- 私有地址
- 視頻課程
- go 微服務搶紅包
- 計算機組成原理+操作系統+計算機網絡
- 計算機組成
- 計算機總線
- 存儲器
- 高速緩存
- 計算機的指令系統
- 計算機的控制器
- 計算機的運算器
- 計算機指令的執行過程
- 進制運算
- 三種編碼方式 原碼 / 補碼 / 反碼
- 定點數 / 浮點數
- 浮點數的運算
- 操作系統
- 進程
- 進程實體
- 五狀態模型
- 進程同步
- 線程同步
- Linux的進程管理
- 進程調度
- 死鎖
- 存儲管理
- 內存分配與回收
- 頁式存儲管理
- 虛擬內存
- Linux的內存管理
- 頁內碎片與頁外碎片
- Budy內存管理算法
- Linux交換空間
- 文件管理
- 文件的邏輯結構
- 輔存的存儲空間分配
- 文件系統
- 文件系統分類
- EXT文件系統
- 設備管理
- 廣義的O設備
- lO設備的緩沖區
- SPOOLing技術
- 線程同步
- 互斥量(鎖)
- 自旋鎖
- 讀寫鎖
- 條件變量
- 線程同步
- fork 創建進程
- Unix域套接字
- 計算機網絡
- ISP
- OSI 七層模型
- 網絡拓撲
- 網絡層 IP
- IP
- 傳輸層 UDP/TCP
- UDP
- TCP
- 可靠傳輸
- 流量控制
- 擁塞控制
- 三次握手
- 四次揮手
- 應用層
- DNS 域名解析
- DHCP 協議
- HTTP 協議
- 編譯原理/操作系統/圖形學
- 一.計算機
- 匯編
- 中斷和中斷向量
- 三.編譯原理
- 編譯器和解釋器
- 編譯流程
- 四.詞法
- 流
- 詞法
- 用狀態機提取詞語(lexer)
- 完整的詞法分析器-多狀態機合并
- 五.抽象語法樹
- 抽象語法樹的繼承 (parser)
- 遞歸法求抽象語法樹
- 表達式樹的驗證
- 塊和語句
- 六.三地址代碼
- 基于 SDD 的翻譯
- 詞法作用域與符號表
- 符號表
- 三地址表示
- 翻譯的整體過程和表達式
- 七. 創建虛擬機
- 用虛擬機執行程序
- 將三地址代碼轉為指令
- 八.操作系統
- 內核
- 九.程序
- 抽象-進程
- 線程
- 競爭條件和臨界區
- 信號量與互斥量
- 十.調度
- 調度
- 優先隊列
- 十一.內存
- 分層存儲
- 垃圾回收
- 地址空間
- 虛擬內存,頁面,MMU
- 程序對內存的管理
- 垃圾回收
- 引用計數
- 標記,掃地,整理
- 分代算法
- 十二.文件系統
- 文件系統和磁盤
- 文件
- 共享文件和目錄
- VFS和基于日志的文件系統
- epoll與select
- 十三.圖形學
- 向量
- 向量的叉積與點積
- 圓的世界
- 矩陣運算
- 三角形網絡
- 渲染圖形
- 十四.WebGL
- 繪制2D圖形
- GLSL
- 圖形渲染管道
- 球面的坐標
- Go微服務入門到容器化實踐,落地可觀測的微服務電商項目
- 第一章 學習指南
- 第二章 微服務與DDD
- 第四章 注冊配置中心實現
- 第六章 熔斷/限流/負載均衡
- 熔斷
- 安裝 Hystrix Dashboard
- 限流
- 負載均衡
- 書籍
- linux鳥哥的私房菜
- 目錄
- 數據結構和算法(Golang實現)
- 遞歸和尾遞歸
- 算法復雜度及漸進符號
- 鏈表
- 字典
- 樹
- 分治法應用
- 快速排序
- 歸并排序
- 排序算法
- 冒泡排序 最差,不推薦
- 選擇排序
- 插入排序
- 希爾排序
- 歸并排序
- 優先隊列及堆排序
- 快速排序
- 查找算法
- 哈希表:散列查找
- 二叉查找樹
- AVL樹 比二叉樹低的樹
- 2-3樹和左傾紅黑樹
- 2-3-4樹和普通紅黑樹
- labuladong的算法小抄
- 第零章、必讀系列
- 學習算法和刷題的框架思維
- 動態規劃解題套路框架
- 回溯算法解題套路框架
- BFS 算法解題套路框架
- 二分搜索
- 滑動窗口算法
- 股票買賣問題
- 常見知識
- 搜索引擎背后的經典數據結構和算法
- 架構師之路
- 消息系統
- QQ狀態同步究竟是推還是拉
- 在線消息可靠傳遞
- 分布式ID生成方法
- 負載均衡
- 數據庫與緩存
- 數據庫軟件架構
- 高并并發下 - 為表新增字段
- 數據庫垂直拆分
- 數據平滑數據遷移
- 數據庫秒級平滑擴容
- 計數系統架構實踐
- 應用層/安全層/傳輸層協議選型
- MQ 消息隊列
- 到底什么時候該使用MQ
- 實現延遲消息
- 實現消息必達
- 定時任務觸發(如用戶離線判斷)
- 超高并發的無鎖緩存
- 連接池實現
- TCP/IP 詳情卷一
- IP:網際協議
- Ping 程序
- UDP 用戶數據報協議
- TCP的超時與重傳
- Go 語言圣經
- 入門
- 鎖的原理
- 互斥鎖
- Goroutines和線程
- 小團隊構建大網站:中小研發團隊架構實踐
- 企業中體架構
- 消息中間鍵 RabbitMQ
- Redis
- 任務調度Job
- 應用監控系統 Metrics
- 集中式日志ELK
- 搜索服務Solr
- 分布式協調器 ZooKeeper
- Jenkins 自動構建
- 單點登錄
- 企業支付網關
- 研發團隊文化是怎么“長”出來的
- HTDP 程序設計方法
- 第二章 數、表達式和簡單程序
- 第七章 數據混合與區分
- 第九章 復合數據類型
- 第十章 表的進一步處理
- 第十一章 處理任意大的自然數
- 第十二章 三論符合函數
- 第十三章 用 list 構造表
- 第十四章 再論自引用數據的定義
- 第十六章 反復精化設計
- 第十七章 處理兩種復雜數據
- 第十八章局部定義和詞匯的范圍
- 代碼大全
- 第三章 三思而后行:前期準備
- 架構的典型組成部分
- 花費在前期準備上的時間長度
- 第五章 軟件構造中的設計
- 理想的設計特征
- 設計的層次
- 常見設計模式
- 第六章 可以工作的類
- 好的抽象
- 良好的類接口
- 有關設計和實現的問題
- 構造函數
- 第七章 高質量的子程序
- 好的子程序名
- 如何使用子程序參數
- 宏子程序和內聯子程序
- 第十章 使用變量的一般事項
- 持續性
- 綁定時間
- 第十一章 變量名的力量
- 選擇好變量名的注意事項
- 為特定類型的數據命名
- 非正式命名規則
- 第十二章基本的數據類型
- 字符和字符串
- 布爾
- 枚舉
- 第十三章 不常見的數據類型
- 結構體
- 指針 [推薦反復查看]
- 第十五章 使用條件語句
- 第十六章 控制控制
- goto
- 第十七章 不常見的控制結構
- 遞歸
- 第十八章 表驅動法
- 直接訪問表
- 索引表訪問
- 階梯訪問表
- 第十九章 一般控制問題
- 減少嵌套層次
- 復雜度的重要性
- 第二十二章 開發者測試
- 第二十四章 重構
- 重構的理由
- 特定的重構
- 語句級的重構
- 子程序級重構
- 類實現的重構
- 類接口的重構
- 系統級重構
- 安全的重構
- 第26章 代碼調整方式
- 循環
- 表達式
- 將子程
- 變得越多,事情反而沒變
- 計算機程序的構造和解釋(SICP)
- 第一章 構造過程抽象
- 1.1 程序設計的基本元素
- 1.3 用高階函數做抽象
- 函數式編程指北
- 第二章 一等公民的函數
- 第三章 純函數的好處
- 第四章 柯里化(curry)
- 第五章 代碼組合(compose)
- 范疇學
- 習題
- 第六章 示例應用
- 聲明式代碼
- 實例項目:獲取圖片
- 第七章 Hindley-Milner 類型簽名
- 第八章 特百惠
- functor / Maybe
- 純錯誤處理
- 包裹函數 - IO
- 異步任務
- 練習
- 第九章 Monad
- pointed functor
- chain
- 練習
- Applicative Functor
- 設計數據密集型應用
- 第一章 可靠性,可擴展性,可維護性
- 第二章 數據模型與查詢語言
- 第三章 數據與索引
- 第四章 編碼與演化
- 第五章 復制
- 第六章 分區
- 第七章 事務
- 第八章 分布式系統的麻煩
- 第九章 一致性與共識
- Unix 編程藝術
- 一.哲學
- 十一:最小立異原則
- 十二.優化
- 十三:復雜度
- 十九:開放源碼:在Uniⅸ新社區 中編程
- 設計模式
- 創建型模式
- 簡單工廠方法模式
- php 示例
- go 示例
- 抽象工廠模式
- php 示例
- go 示例
- 生成器模式
- php 示例
- go 示例
- 原型模式 - 克隆
- php 示例
- go 示例
- 單例模式
- php 示例
- go 示例
- 結構型模式
- 適配器模式
- php 示例
- go 示例
- 橋接模式 [??]
- php 示例
- go 示例
- 組合模式
- php 示例
- go 示例
- 裝飾模式 - 鉤子 [???]
- php 示例
- go 示例
- 外觀模式
- php 示例
- go 示例
- 享元模式
- go 示例
- 代理模式 [???]
- php 示例
- go 示例
- 行為模式
- 責任鏈模式[???]
- php 示例
- go 示例
- 命令模式
- php 示例
- go 示例
- 迭代器模式
- php 示例
- go 示例
- 中介者模式
- php 示例
- go 示例
- 備忘錄模式
- php 示例
- go 示例
- 觀察者(發布訂閱)模式[???]
- php 示例
- go 示例
- 狀態模式 - 狀態機
- php 示例
- go 示例
- 策略模式[???]
- php 示例
- go 示例
- 模板方法[???]
- php 示例
- go 示例
- 訪問者模式
- php 示例
- go 示例
- 數據結構
- 數組
- 雙指針
- 字符串
- 找子串
- 棧 / 隊列
- 循環隊列
- 列表 List
- 排序算法
- 鏈表
- 遍歷
- 翻轉鏈表
- 樹
- 二叉樹
- 二叉樹遍歷
- DFS 深度優先
- BFS 廣度優先
- 示例
- 二叉樹的最大深度
- 對稱二叉樹
- 將有序數組轉換為二叉搜索樹
- 算法
- 查找算法
- KMP 算法
- 跳表
- Sunday算法
- 動態規劃
- 爬樓梯
- 最大子序和
- 零錢問題
- 分布式算法
- Raft
- hashicorp/raft go 實現
- 貝葉斯算法
- python 示例
- 人工智能
- 知識
- 基礎概念與入門案例
- 語言模型
- 注意力機制
- Transformers pipelines
- 開源項目
- DiffBIR 圖片項目
- TokenFlow 視頻語言渲染
- ProPainter 去除視頻人物
- CodeFormer 圖片畫質增強
- yolov5 物品識別
- 訓練自己的模型
- Donut 無需OCR識別圖片內容
- ott 翻譯
- VideoPipe 視頻物品識別
- ollama
- 基礎庫
- PyTorch
- 安裝
- TensorFlow
- 大語言模型架構
- Awesome
- JittorLLMs
- huggingface
- transformers
- pipeline 的處理流程
- 離線模式
- 模型處理
- 示例
- 常用 pipelines
- 使用gpt2
- 翻譯
- Q&A
- 匯編
- MIPS
- 指令集
- 加載/保存 指令集
- 算術指令集
- 控制流 指令集
- SS, SP, BP 三個寄存器
- 音視頻
- 知識
- 幾種瀏覽器播放RTSP視頻流解決方案
- 流媒體播放格式
- 流媒體傳輸協議(rtp/rtcp/rtsp/rtmp/)
- 常用工具/庫
- EasyDarwin
- EasyDarwin RTSP流媒體服務器-GO
- EasyPusher
- EasyDSS 非開源 RTMP
- EasyScreenLive 錄制推流
- ZLMediaKit 流媒體服務框架 c++
- 基于ZLMediaKit的UI
- lal 流媒體服務器 GOLANG
- go2rtc 支持各種流媒體協議
- RTP/RTCP
- RTP
- RTCP
- RTSP
- 知識
- RTSP/RTP 交錯傳輸方式
- RTP timestamp
- rtsp組播
- 語法
- OPTIONS 詢問
- DESCRIBE 詢問SDP
- SETUP 設置傳輸模式
- PLAY 啟動
- PAUSE 暫停
- TEARDOWN 終止
- SET_PARAMETER 生成一個I幀
- GET_PARAMETER 查詢參數狀態
- RTSP 響應狀態碼
- 示例
- ffmpeg 推流到rtsp服務器基于udp
- ffplay 拉取rtsp流,基于udp
- ============
- ffmpeg 推流到rtsp服務器基于tcp
- ffplay 拉取基于TCP的rtsp流
- ===========
- EasyScreenLive 推送rtsp服務器 基于tcp
- RTMP
- 術語
- 消息和塊的區別
- 協議流程
- 分塊
- RTMP消息格式
- RTMP消息類型
- 視頻協議
- H.264
- STUN / TURN
- MCU合流
- SDP協議
- SIP
