# 一、數據科學的生命周期 > 原文：[DS-100/textbook/notebooks/ch01](https://nbviewer.jupyter.org/github/DS-100/textbook/tree/master/notebooks/ch01/) > > 校驗：[飛龍](https://github.com/wizardforcel) > > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 在數據科學中，我們使用大量不同的數據集來對世界做出結論。在這個課程中，我們將通過計算和推理思維的雙重視角，來討論數據科學的關鍵原理和技術。實際上，這涉及以下過程： + 提出一個問題 + 獲取和清理數據 + 進行探索性數據分析 + 用預測和推理得出結論 在這個過程的最后一步之后，通常出現更多的問題，因此我們可以反復地執行這個過程，來發現我們的世界的新特征。這個正反饋的循環對我們的工作至關重要，我們稱之為數據科學生命周期。 如果數據科學的生命周期與它說的一樣容易進行，那么就不需要該主題的教科書了。幸運的是，生命周期中的每個步驟都包含眾多挑戰，這些挑戰揭示了強大和通常令人驚訝的見解，它們構成了使用數據在思考后進行決策的基礎。 和 Data8 一樣，我們將以一個例子開始。 > 譯者注：Data8 是 DS100 是先修課。我之前翻譯了它的課本，[《計算與推斷思維 中文版》](https://github.com/Kivy-CN/data8-textbook-zh)。 ## 關于本書 在我們繼續之前，重要的是說出我們對讀者的假設。 在本書中，我們將當作你已經上完了 Data8 或者其他一些類似的東西。 特別是，我們假定你對以下主題有一定了解（同時給出 Data8 課本的頁面鏈接）。 + [表格數據處理：選擇，過濾，分組，連接](https://github.com/Kivy-CN/data8-textbook-zh/blob/master/5.md) + [抽樣，統計的經驗分布](https://github.com/Kivy-CN/data8-textbook-zh/blob/master/9.md) + [使用自舉重采樣的假設檢驗](https://github.com/Kivy-CN/data8-textbook-zh/blob/master/10.md) + [最小二乘回歸和回歸推斷](https://github.com/Kivy-CN/data8-textbook-zh/blob/master/14.md) + [分類](https://github.com/Kivy-CN/data8-textbook-zh/blob/master/15.md) 另外，我們假設你已經上完了 CS61A 或者其他類似的東西，因此除了特殊情況外，不會解釋 Python 的語法。 > 譯者注：CS61A（SICP Python）是計算機科學的第一門課，中文版講義請見[《SICP Python 中文版》](https://github.com/Kivy-CN/sicp-py-zh)。 ## DS100 的學生 回想一下，數據科學生命周期涉及以下大致的步驟： + 問題表述： + 我們想知道什么，或者我們想要解決什么問題？ + 我們的假設是什么？ + 我們的成功指標是什么？ + 數據采集和清洗： + 我們有什么數據以及需要哪些數據？ + 我們將如何收集更多數據？ + 我們如何組織數據來分析？ + 探索性數據分析： + 我們是否有了相關數據？ + 數據有哪些偏差，異常或其他問題？ + 我們如何轉換數據來實現有效的分析？ + 預測和推斷： + 這些數據說了世界的什么事情？ + 它回答我們的問題，還是準確地解決問題？ + 我們的結論有多健壯？ ### 問題表述 我們想知道 DS100 中的學生姓名的數據，是否向我們提供了學生本身的其他信息。 雖然這是一個模糊的問題，但這足以讓我們處理我們的數據，我們當然可以在問題變得更加精確的時候提出問題。 ### 數據采集和清洗 在 DS100 中，我們將研究收集數據的各種方法。 我們首先看看我們的數據，這是我們從以前的 DS100 課程中下載的學生姓名的名單。 如果你現在不了解代碼，請不要擔心；我們稍后會更深入地介紹這些庫。 相反，請關注我們展示的流程和圖表。 ```py import pandas as pd students = pd.read_csv('roster.csv') students ``` | | Name | Role | | --- | --- | --- | | 0 | Keeley | Student | | 1 | John | Student | | 2 | BRYAN | Student | | ... | ... | ... | | 276 | Ernesto | Waitlist Student | | 277 | Athan | Waitlist Student | | 278 | Michael | Waitlist Student | 279 行 × 2 列 我們很快可以看到，數據中有一些奇怪的東西。 例如，其中一個學生的姓名全部是大寫字母。 另外，`Role`列的作用并不明顯。 在 DS100 中，我們將研究如何識別數據中的異常并執行修正。 大寫字母的差異將導致我們的程序認為`'BRYAN'`和`'Bryan'`是不同的名稱，但他們對于我們的目標是相同的。 我們將所有名稱轉換為小寫來避免這種情況。 ```py students['Name'] = students['Name'].str.lower() students ``` | | Name | Role | | --- | --- | --- | | 0 | keeley | Student | | 1 | john | Student | | 2 | bryan | Student | | ... | ... | ... | | 276 | ernesto | Waitlist Student | | 277 | athan | Waitlist Student | | 278 | michael | Waitlist Student | 279 行 × 2 列 現在我們的數據有了更容易處理的格式，我們繼續進行探索性數據分析。 ## 探索性數據分析（EDA） 術語探索性數據分析（簡稱 EDA）是指發現我們的數據特征的過程，這些特征為未來的分析提供信息。 這是上一頁的`students`表： ```py students ``` | | Name | Role | | --- | --- | --- | | 0 | keeley | Student | | 1 | john | Student | | 2 | bryan | Student | | ... | ... | ... | | 276 | ernesto | Waitlist Student | | 277 | athan | Waitlist Student | | 278 | michael | Waitlist Student | 279 行 × 2 列 我們留下了許多問題。 這個名單中有多少名學生？ `Role`列是什么意思？ 我們進行 EDA 來更全面地了解我們的數據。 在 DS100 中，我們將研究探索性數據分析和實踐，來分析新數據集。 通常，我們通過重復提出簡單問題，他們有關我們想知道的數據，來探索數據。 我們將以這種方式構建我們的分析。 我們的數據集中有多少學生？ ```py print("There are", len(students), "students on the roster.") # There are 279 students on the roster. ``` 一個自然的后續問題是，這是否是完整的學生名單。 在這種情況下，我們碰巧知道這個列表包含班級中的所有學生。 `Role`字段的含義是什么？ 理解字段的含義，通常可以通過查看字段數據的唯一值來實現： ```py students['Role'].value_counts().to_frame() ``` | | Role | | --- | --- | | Student | 237 | | Waitlist Student | 42 | 我們可以在這里看到，我們的數據不僅包含當時注冊了課程的學生，還包含等候名單上的學生。 `Role`列告訴我們每個學生是否注冊。 那名稱呢？ 我們如何總結這個字段？ 在 DS100 中，我們將處理許多不同類型的數據（不僅僅是數字），而且我們將研究面向不同類型的數據的技術。 好的起點可能是檢查字符串的長度。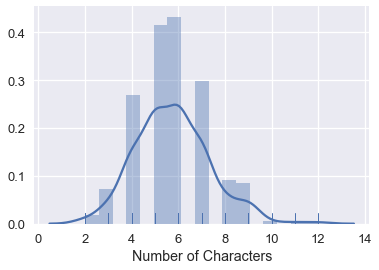 ```py sns.distplot(students['Name'].str.len(), rug=True, axlabel="Number of Characters") # <matplotlib.axes._subplots.AxesSubplot at 0x10e6fd0b8> ```  這種可視化向我們展示了，大多數名稱的長度在 3 到 9 個字符之間。 這給了我們一個機會，來檢查我們的數據是否合理 - 如果有很多名稱長度為 1 個字符，我們就有充分的理由重新檢查我們的數據。 ### 名稱里面有什么？ 雖然這個數據集非常簡單，但我們很快就會看到，僅僅是名稱就可以揭示我們班級的相當多的信息。 ## 名稱里面有什么 到目前為止，我們已經對我們的數據提出了一個大致的問題：“DS100 中的學生名稱是否告訴我們該課程的任何信息？” 通過將所有名稱轉換為小寫字母，我們完成一些數據清理工作。 在我們的探索性數據分析過程中，我們發現，我們的名單包含班級和候補名單中的大約 270 個學生姓名，而大部分名稱長度在 4 到 8 個字符之間。 根據名稱，我們還能發現班級的什么其他信息？ 我們可能會考慮數據集中的單個名稱： ```py students['Name'][5] # 'jerry' ``` 從這個名稱中我們可以推斷出，這個學生可能是一個男生。我們也可以猜測學生的年齡。例如，如果我們知道，杰里在 1998 年是一個非常受歡迎的嬰兒名稱，那么我們可能會猜測這個學生大約二十歲。 這個想法給了我們兩個需要調查的新問題： + “DS100 中的學生名稱，是否告訴了我們課堂上的性別分布？” + “DS100 中的第一批學生，是否告訴了我們課堂上的年齡分布？” 為了調查這些問題，我們需要一個數據集，它將姓名與性別和年份相關聯。方便的是，美國社會保障部門在線提供這樣一個數據集：<https://www.ssa.gov/oact/babynames/index.html>。他們的數據集記錄了嬰兒出生時的名稱，因此通常稱為嬰兒名稱數據集。 我們將從下載開始，然后將數據集加載到 Python 中。再次，不要擔心理解第一章中的代碼。理解整個過程更重要。 ```py import urllib.request import os.path data_url = "https://www.ssa.gov/oact/babynames/names.zip" local_filename = "babynames.zip" if not os.path.exists(local_filename): # if the data exists don't download again with urllib.request.urlopen(data_url) as resp, open(local_filename, 'wb') as f: f.write(resp.read()) import zipfile babynames = [] with zipfile.ZipFile(local_filename, "r") as zf: data_files = [f for f in zf.filelist if f.filename[-3:] == "txt"] def extract_year_from_filename(fn): return int(fn[3:7]) for f in data_files: year = extract_year_from_filename(f.filename) with zf.open(f) as fp: df = pd.read_csv(fp, names=["Name", "Sex", "Count"]) df["Year"] = year babynames.append(df) babynames = pd.concat(babynames) babynames ``` | | Name | Sex | Count | Year | | --- | --- | --- | --- | --- | | 0 | Mary | F | 9217 | 1884 | | 1 | Anna | F | 3860 | 1884 | | 2 | Emma | F | 2587 | 1884 | | ... | ... | ... | ... | ... | | 2081 | Verna | M | 5 | 1883 | | 2082 | Winnie | M | 5 | 1883 | | 2083 | Winthrop | M | 5 | 1883 | 1891894 行 × 4 列 ``` ls -alh babynames.csv # -rw-r--r-- 1 sam staff 30M Jan 22 15:31 babynames.csv ``` 看起來，數據集包含名稱，嬰兒性別，具有該名稱的嬰兒數量以及這些嬰兒的出生年份。 為了確認，我們從檢查來自 SSN 的數據集描述：<https://www.ssa.gov/oact/babynames/background.html>。 > 所有名稱均來自 1879 年后美國出生人口的社保卡申請。請注意，很多 1937 年以前出生的人從未申請過社保卡，所以他們的名字不包含在我們的數據中。 對于其他申請人，我們的記錄可能不會顯示出生地點，并且他們的姓名也不會包含在我們的數據中。 > > 所有數據均來自截至我們的 2017 年 3 月社保卡申請記錄的 100% 樣本。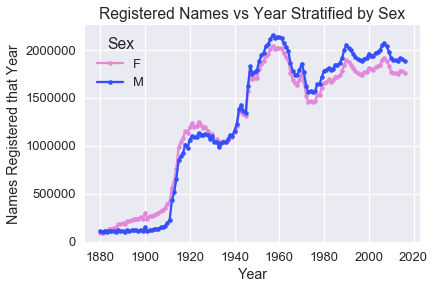 這個數據的一個有用的可視化，是繪制每年出生的男性和女性嬰兒的數量： ```py pivot_year_name_count = pd.pivot_table( babynames, index='Year', columns='Sex', values='Count', aggfunc=np.sum) pink_blue = ["#E188DB", "#334FFF"] with sns.color_palette(sns.color_palette(pink_blue)): pivot_year_name_count.plot(marker=".") plt.title("Registered Names vs Year Stratified by Sex") plt.ylabel('Names Registered that Year') ```  這個繪圖讓我們質疑，1880 年的美國是否有嬰兒。上面引用的一句話有助于解釋： > 請注意，很多 1937 年以前出生的人從未申請過社保卡，所以他們的名字不包含在我們的數據中。 對于其他申請人，我們的記錄可能不會顯示出生地點，并且他們的姓名也不會包含在我們的數據中。 我們還可以在上圖中清楚地看到嬰兒潮的時期。 ### 從名字推斷性別 我們使用這個數據集來估計我們班的男女生人數。 與我們班的名單一樣，我們先將名稱小寫： ```py babynames['Name'] = babynames['Name'].str.lower() babynames ``` | | Name | Sex | Count | Year | | --- | --- | --- | --- | --- | | 0 | mary | F | 9217 | 1884 | | 1 | anna | F | 3860 | 1884 | | 2 | emma | F | 2587 | 1884 | | ... | ... | ... | ... | ... | | 2081 | verna | M | 5 | 1883 | | 2082 | winnie | M | 5 | 1883 | | 2083 | winthrop | M | 5 | 1883 | 1891894 行 × 4 列 然后，我們計算對于每個名字，共有多少個男嬰和女嬰出生： ```py sex_counts = pd.pivot_table(babynames, index='Name', columns='Sex', values='Count', aggfunc='sum', fill_value=0., margins=True) sex_counts ``` | Sex | F | M | All | | ---| --- | --- | --- | | Name | | | | | aaban | 0 | 96 | 96 | | aabha | 35 | 0 | 35 | | aabid | 0 | 10 | 10 | | ... | ... | ... | ... | | zyyon | 0 | 6 | 6 | | zzyzx | 0 | 5 | 5 | | All | 170639571 | 173894326 | 344533897 | 96175 行 × 3 列 為了決定一個名字是男性還是女性，我們可以計算出這個名字給女性嬰兒的次數比例。 ```py prop_female = sex_counts['F'] / sex_counts['All'] sex_counts['prop_female'] = prop_female sex_counts ``` | Sex | F | M | All | prop_female | | ---| --- | --- | --- | --- | | Name | | | | | | aaban | 0 | 96 | 96 | 0.000000 | | aabha | 35 | 0 | 35 | 1.000000 | | aabid | 0 | 10 | 10 | 0.000000 | | ... | ... | ... | ... | ... | | zyyon | 0 | 6 | 6 | 0.000000 | | zzyzx | 0 | 5 | 5 | 0.000000 | | All | 170639571 | 173894326 | 344533897 | 0.495277 | 96175 行 × 4 列 然后，我們可以定義一個函數，查找給定名稱的女性比例。 ```py def sex_from_name(name): if name in sex_counts.index: prop = sex_counts.loc[name, 'prop_female'] return 'F' if prop > 0.5 else 'M' else: return None sex_from_name('sam') # 'M' ``` 嘗試在這個框中輸入一些名稱，來查看這個函數是否輸出你期望的內容： ```py interact(sex_from_name, name='sam'); ``` 我們在班級名單中，使用最可能的性別標記每個名稱。 ```py students['sex'] = students['Name'].apply(sex_from_name) students ``` | | Name | Role | sex | | --- | --- | --- | --- | | 0 | keeley | Student | F | | 1 | john | Student | M | | 2 | bryan | Student | M | | ... | ... | ... | ... | | 276 | ernesto | Waitlist Student | M | | 277 | athan | Waitlist Student | M | | 278 | michael | Waitlist Student | M | 279 行 × 3 列 現在，估計我們有多少男女學生就很容易了： ```py students['sex'].value_counts() ''' M 144 F 92 Name: sex, dtype: int64 ''' ``` ### 從名稱推斷年齡 我們可以采用類似的方法來估計班級的年齡分布，將每個姓名映射到數據集中的平均年齡。 ```py def avg_year(group): return np.average(group['Year'], weights=group['Count']) avg_years = ( babynames .groupby('Name') .apply(avg_year) .rename('avg_year') .to_frame() ) avg_years ``` | | avg_year | | --- | --- | | Name | | | aaban | 2012.572917 | | aabha | 2013.714286 | | aabid | 2009.500000 | | ... | ... | | zyyanna | 2010.000000 | | zyyon | 2014.000000 | | zzyzx | 2010.000000 | 96174 行 × 1 列 ```py def year_from_name(name): return (avg_years.loc[name, 'avg_year'] if name in avg_years.index else None) # Generate input box for you to try some names out: interact(year_from_name, name='fernando'); students['year'] = students['Name'].apply(year_from_name) students ``` | | Name | Role | sex | year | | --- | --- | --- | --- | --- | | 0 | keeley | Student | F | 1998.147952 | | 1 | john | Student | M | 1951.084937 | | 2 | bryan | Student | M | 1983.565113 | | ... | ... | ... | ... | ... 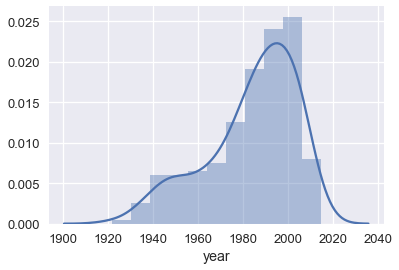| | 276 | ernesto | Waitlist Student | M | 1981.439873 | | 277 | athan | Waitlist Student | M | 2004.397863 | | 278 | michael | Waitlist Student | M | 1971.179231 | 279 行 × 4 列 之后，繪制年份的分布情況很容易： ```py sns.distplot(students['year'].dropna()); ```  為了計算平均年份： ```py students['year'].mean() # 1983.846741800525 ``` 這使得它看起來像是，學生平均是 35 歲。 這是一個大學本科課程，所以我們預計平均年齡在 20 歲左右。為什么我們的估計會如此之遠？ 作為數據科學家，我們經常遇到不符合我們預期的結果，并且必須做出判斷，我們的結果是由我們的數據，我們的流程還是不正確的假設造成的。 不可能定義適用于所有情況的規則。 相反，我們將為你提供工具來重新檢查數據分析的每一步，并告訴你如何使用它們。 在這種情況下，我們意想不到的結果，最可能是因為大多數名字都是舊的。 例如，在我們的數據記錄中，約翰這個名字在整個歷史中都相當流行，這意味著我們可能會猜測約翰出生于 1950 年左右。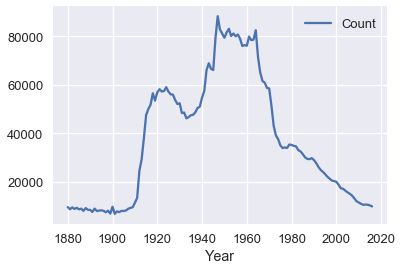我們可以通過查看數據來確認： ```py names = babynames.set_index('Name').sort_values('Year') john = names.loc['john'] john[john['Sex'] == 'M'].plot('Year', 'Count'); ```  如果我們相信，我們班沒有人超過 40 歲或低于 10 歲（我們可以通過在課上觀察我們的教室發現），我們可以通過僅檢查 1978 年之間的數據，將其納入我們的分析中。我們將很快討論數據操作，并且你可能會重新分析這個示例，來確定納入這一先驗是否會提供更明智的結果。