# 沃爾瑪數據集 > 原文：[https://www.textbook.ds100.org/ch/14/feature ou one_hot.html](https://www.textbook.ds100.org/ch/14/feature ou one_hot.html) ``` # HIDDEN # Clear previously defined variables %reset -f # Set directory for data loading to work properly import os os.chdir(os.path.expanduser('~/notebooks/14')) ``` ``` # HIDDEN import warnings # Ignore numpy dtype warnings. These warnings are caused by an interaction # between numpy and Cython and can be safely ignored. # Reference: https://stackoverflow.com/a/40846742 warnings.filterwarnings("ignore", message="numpy.dtype size changed") warnings.filterwarnings("ignore", message="numpy.ufunc size changed") import numpy as np import matplotlib.pyplot as plt import pandas as pd import seaborn as sns %matplotlib inline import ipywidgets as widgets from ipywidgets import interact, interactive, fixed, interact_manual import nbinteract as nbi sns.set() sns.set_context('talk') np.set_printoptions(threshold=20, precision=2, suppress=True) pd.options.display.max_rows = 7 pd.options.display.max_columns = 8 pd.set_option('precision', 2) # This option stops scientific notation for pandas # pd.set_option('display.float_format', '{:.2f}'.format) ``` 2014 年，沃爾瑪發布了一些銷售數據，作為預測其商店每周銷售額的競爭的一部分。我們已經獲取了他們數據的一個子集，并將其加載到下面。 ``` walmart = pd.read_csv('walmart.csv') walmart ``` | | 日期 | 每周銷售 | 伊索利德 | 溫度 | 燃料價格 | 失業 | 降價 | | --- | --- | --- | --- | --- | --- | --- | --- | | 零 | 2010 年 2 月 5 日 | 24924.50 美元 | 不 | 四十二點三一 | 二點五七二 | 八點一零六 | 無降價 | | --- | --- | --- | --- | --- | --- | --- | --- | | 1 個 | 2010 年 2 月 12 日 | 46039.49 元 | 是的 | 三十八點五一 | 二點五四八 | 8.106 | No Markdown | | --- | --- | --- | --- | --- | --- | --- | --- | | 二 | 2010 年 2 月 19 日 | 41595.55 美元 | No | 三十九點九三 | 二點五一四 | 8.106 | No Markdown | | --- | --- | --- | --- | --- | --- | --- | --- | | …… | …… | ... | ... | ... | ... | ... | ... | | --- | --- | --- | --- | --- | --- | --- | --- | | 一百四十 | 2012 年 10 月 12 日 | 22764.01 年 | No | 六十二點九九 | 三點六零一 | 六點五七三 | 降價 2 | | --- | --- | --- | --- | --- | --- | --- | --- | | 一百四十一 | 2012 年 10 月 19 日 | 24185.27 美元 | No | 六十七點九七 | 三點五九四 | 6.573 | MarkDown2 | | --- | --- | --- | --- | --- | --- | --- | --- | | 一百四十二 | 2012 年 10 月 26 日 | 27390.81 元 | No | 六十九點一六 | 三點五零六 | 6.573 | 降價 1 | | --- | --- | --- | --- | --- | --- | --- | --- | 143 行×7 列 這些數據包含幾個有趣的特性，包括一周是否包含假日（`IsHoliday`）、那周的失業率（`Unemployment`），以及商店在那一周提供哪些特價商品（`MarkDown`）。 我們的目標是創建一個模型，使用數據中的其他變量預測`Weekly_Sales`變量。使用線性回歸模型，我們可以直接使用`Temperature`、`Fuel_Price`和`Unemployment`列，因為它們包含數值數據。 ## 使用 SciKit Learn[?](#Fitting-a-Model-Using-Scikit-Learn)擬合模型 在前面的部分中，我們已經了解了如何獲取成本函數的梯度，并使用梯度下降來擬合模型。為此，我們必須為模型定義 python 函數、成本函數、成本函數的梯度和梯度下降算法。雖然這對于演示概念如何工作很重要，但在本節中，我們將使用名為[`scikit-learn`](http://scikit-learn.org/)的機器學習庫，它允許我們用更少的代碼來適應模型。 例如，為了使用沃爾瑪數據集中的數值列來擬合多重線性回歸模型，我們首先創建一個包含用于預測的變量的二維 numpy 數組和一個包含我們想要預測的值的一維數組： ``` numerical_columns = ['Temperature', 'Fuel_Price', 'Unemployment'] X = walmart[numerical_columns].as_matrix() X ``` ``` array([[ 42.31, 2.57, 8.11], [ 38.51, 2.55, 8.11], [ 39.93, 2.51, 8.11], ..., [ 62.99, 3.6 , 6.57], [ 67.97, 3.59, 6.57], [ 69.16, 3.51, 6.57]]) ``` ``` y = walmart['Weekly_Sales'].as_matrix() y ``` ``` array([ 24924.5 , 46039.49, 41595.55, ..., 22764.01, 24185.27, 27390.81]) ``` 然后，我們從`scikit-learn`（[docs](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression)）導入`LinearRegression`類，實例化它，并使用`X`調用`fit`方法來預測`y`。 請注意，以前我們必須手動將所有$1$的列添加到`X`矩陣中，以便進行截距線性回歸。這一次，`scikit-learn`將在幕后處理截獲列，為我們節省一些工作。 ``` from sklearn.linear_model import LinearRegression simple_classifier = LinearRegression() simple_classifier.fit(X, y) ``` ``` LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False) ``` 我們完了！當我們調用`.fit`時，`scikit-learn`找到線性回歸參數，使最小二乘成本函數最小化。我們可以看到以下參數： ``` simple_classifier.coef_, simple_classifier.intercept_ ``` ``` (array([ -332.22, 1626.63, 1356.87]), 29642.700510138635) ``` 為了計算均方成本，我們可以要求分類器對輸入數據`X`進行預測，并將預測值與實際值`y`進行比較。 ``` predictions = simple_classifier.predict(X) np.mean((predictions - y) ** 2) ``` ``` 74401210.603607252 ``` 平均平方誤差看起來相當高。這很可能是因為我們的變量（溫度、燃料價格和失業率）與每周銷售的相關性很弱。 我們的數據中還有兩個變量可能對預測更有用：列`IsHoliday`和列`MarkDown`。下面的框線圖顯示假日可能與周銷售額有一定關系。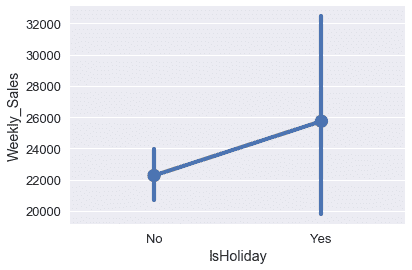 ``` sns.pointplot(x='IsHoliday', y='Weekly_Sales', data=walmart); ```  不同的降價類別似乎與不同的周銷售額密切相關。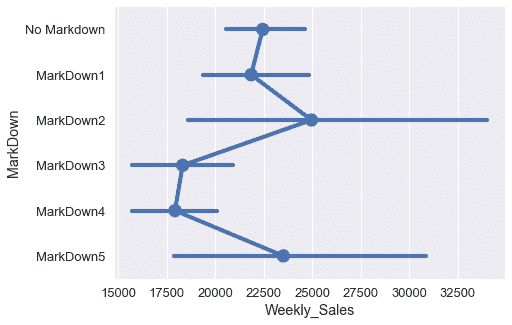 ``` markdowns = ['No Markdown', 'MarkDown1', 'MarkDown2', 'MarkDown3', 'MarkDown4', 'MarkDown5'] plt.figure(figsize=(7, 5)) sns.pointplot(x='Weekly_Sales', y='MarkDown', data=walmart, order=markdowns); ```  然而，`IsHoliday`和`MarkDown`列都包含分類數據，而不是數字數據，因此我們不能像回歸那樣使用它們。 ## 一個熱編碼 幸運的是，我們可以對這些分類變量執行**一次熱編碼**轉換，將它們轉換為數字變量。轉換的工作方式如下：為類別變量中的每個唯一值創建一個新列。如果變量最初具有相應的值，則該列包含$1$，否則該列包含$0$。例如，下面的`MarkDown`列包含以下值： ``` # HIDDEN walmart[['MarkDown']] ``` | | MarkDown | | --- | --- | | 0 | No Markdown | | --- | --- | | 1 | No Markdown | | --- | --- | | 2 | No Markdown | | --- | --- | | ... | ... | | --- | --- | | 140 | MarkDown2 | | --- | --- | | 141 | MarkDown2 | | --- | --- | | 142 | MarkDown1 | | --- | --- | 143 行×1 列 此變量包含六個不同的唯一值：“no markdown”、“markdown1”、“markdown2”、“markdown3”、“markdown4”和“markdown5”。我們為每個值創建一列，以獲得總共六列。然后，我們按照上面描述的方案用零和一填充列。 ``` # HIDDEN from sklearn.feature_extraction import DictVectorizer items = walmart[['MarkDown']].to_dict(orient='records') encoder = DictVectorizer(sparse=False) pd.DataFrame( data=encoder.fit_transform(items), columns=encoder.feature_names_ ) ``` | | markdown=降價 1 | markdown=降價 2 | markdown=降價 3 | markdown=降價 4 | markdown=降價 5 | 降價=無降價 | | --- | --- | --- | --- | --- | --- | --- | | 0 | 零 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 條 | | --- | --- | --- | --- | --- | --- | --- | | 1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | | --- | --- | --- | --- | --- | --- | --- | | 2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | | --- | --- | --- | --- | --- | --- | --- | | ... | ... | ... | ... | ... | ... | ... | | --- | --- | --- | --- | --- | --- | --- | | 140 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | | --- | --- | --- | --- | --- | --- | --- | | 141 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | | --- | --- | --- | --- | --- | --- | --- | | 142 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | | --- | --- | --- | --- | --- | --- | --- | 143 行×6 列 請注意，數據中的第一個值是“無降價”，因此只有轉換表中第一行的最后一列標記為$1$。此外，數據中的最后一個值是“markdown1”，這導致第 142 行的第一列標記為$1$。 結果表的每一行將包含一個包含$1$的列；其余的將包含$0$的列。名稱“one hot”反映了這樣一個事實：只有一列是“hot”（標記為$1$）。 ## SciKit 學習[?](#One-Hot-Encoding-in-Scikit-Learn)中的一個熱編碼 要執行一個熱編碼，我們可以使用`scikit-learn`的[`DictVectorizer`](http://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.DictVectorizer.html)類。要使用這個類，我們必須將數據框架轉換為字典列表。dictvectorizer 類自動對分類數據（需要是字符串）進行一次熱編碼，并保持數字數據不變。 ``` from sklearn.feature_extraction import DictVectorizer all_columns = ['Temperature', 'Fuel_Price', 'Unemployment', 'IsHoliday', 'MarkDown'] records = walmart[all_columns].to_dict(orient='records') encoder = DictVectorizer(sparse=False) encoded_X = encoder.fit_transform(records) encoded_X ``` ``` array([[ 2.57, 1\. , 0\. , ..., 1\. , 42.31, 8.11], [ 2.55, 0\. , 1\. , ..., 1\. , 38.51, 8.11], [ 2.51, 1\. , 0\. , ..., 1\. , 39.93, 8.11], ..., [ 3.6 , 1\. , 0\. , ..., 0\. , 62.99, 6.57], [ 3.59, 1\. , 0\. , ..., 0\. , 67.97, 6.57], [ 3.51, 1\. , 0\. , ..., 0\. , 69.16, 6.57]]) ``` 為了更好地理解轉換后的數據，我們可以用列名顯示它： ``` pd.DataFrame(data=encoded_X, columns=encoder.feature_names_) ``` | | Fuel_Price | isholiday=否 | isholiday=是 | MarkDown=MarkDown1 | ... | MarkDown=MarkDown5 | MarkDown=No Markdown | Temperature | Unemployment | | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | | 0 | 2.572 | 1.0 | 0.0 | 0.0 | ... | 0.0 | 1.0 | 42.31 | 8.106 | | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | | 1 | 2.548 | 0.0 | 1.0 | 0.0 | ... | 0.0 | 1.0 | 38.51 | 8.106 | | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | | 2 | 2.514 | 1.0 | 0.0 | 0.0 | ... | 0.0 | 1.0 | 39.93 | 8.106 | | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | | 140 | 3.601 | 1.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 62.99 | 6.573 | | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | | 141 | 3.594 | 1.0 | 0.0 | 0.0 | ... | 0.0 | 0.0 | 67.97 | 6.573 | | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | | 142 | 3.506 | 1.0 | 0.0 | 1.0 | ... | 0.0 | 0.0 | 69.16 | 6.573 | | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | 143 行×11 列 數值變量（燃油價格、溫度和失業率）保留為數字。分類變量（假日和降價）是一個熱編碼。當我們使用新的數據矩陣來擬合線性回歸模型時，我們將為每列數據生成一個參數。因為這個數據矩陣包含 11 列，所以模型將有 12 個參數，因為我們為截距項設置了額外的參數。 ## 用轉換后的數據擬合模型 我們現在可以使用`encoded_X`變量進行線性回歸。 ``` clf = LinearRegression() clf.fit(encoded_X, y) ``` ``` LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False) ``` 如前所述，我們有十一個列參數和一個截距參數。 ``` clf.coef_, clf.intercept_ ``` ``` (array([ 1622.11, -2.04, 2.04, 962.91, 1805.06, -1748.48, -2336.8 , 215.06, 1102.25, -330.91, 1205.56]), 29723.135729284979) ``` 我們可以比較兩個分類器的一些預測，看看兩者之間是否有很大的區別。 ``` walmart[['Weekly_Sales']].assign( pred_numeric=simple_classifier.predict(X), pred_both=clf.predict(encoded_X) ) ``` | | Weekly_Sales | pred 數字 | 兩者皆可預測 | | --- | --- | --- | --- | | 0 | 24924.50 | 30768.878035 | 30766.790214 年 | | --- | --- | --- | --- | | 1 | 46039.49 | 31992.279504 | 31989.410395 年 | | --- | --- | --- | --- | | 2 | 41595.55 | 31465.220158 號 | 31460.280008 個 | | --- | --- | --- | --- | | ... | ... | ... | ... | | --- | --- | --- | --- | | 140 | 22764.01 | 23492.262649 | 24447.348979 個 | | --- | --- | --- | --- | | 141 | 24185.27 | 21826.414794 個 | 22788.049554 個 | | --- | --- | --- | --- | | 142 | 27390.81 | 21287.928537 | 21409.367463 號 | | --- | --- | --- | --- | 143 行×3 列 這兩個模型的預測似乎非常相似。兩組預測的散點圖證實了這一點。 ``` plt.scatter(simple_classifier.predict(X), clf.predict(encoded_X)) plt.title('Predictions using all data vs. 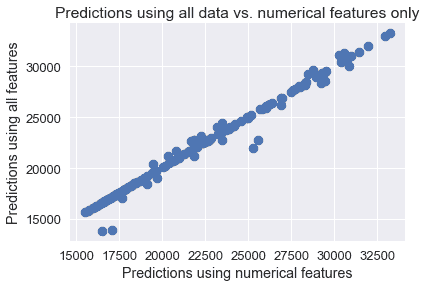numerical features only') plt.xlabel('Predictions using numerical features') plt.ylabel('Predictions using all features'); ```  ## 模型診斷 為什么會這樣？我們可以檢查兩個模型學習的參數。下表顯示了分類器所獲得的權重，該分類器只使用數值變量而不使用一個熱編碼： ``` # HIDDEN def clf_params(names, clf): weights = ( np.append(clf.coef_, clf.intercept_) ) return pd.DataFrame(weights, names + ['Intercept']) clf_params(numerical_columns, simple_classifier) ``` | | 0 | | --- | --- | | Temperature | -332.221180 個 | | --- | --- | | Fuel_Price | 1626.625604 年 | | --- | --- | | Unemployment | 1356.868319 號 | | --- | --- | | 攔截 | 29642.700510 個 | | --- | --- | 下表顯示了使用一個熱編碼的分類器學習的權重。 ``` # HIDDEN pd.options.display.max_rows = 13 display(clf_params(encoder.feature_names_, clf)) pd.options.display.max_rows = 7 ``` | | 0 | | --- | --- | | Fuel_Price | 1622.106239 年 | | --- | --- | | IsHoliday=No | -2.041451 年 | | --- | --- | | IsHoliday=Yes | 2.041451 年 | | --- | --- | | MarkDown=MarkDown1 | 962.908849 號 | | --- | --- | | MarkDown=MarkDown2 | 1805.059613 年 | | --- | --- | | MarkDown=MarkDown3 | -1748.475046 年 | | --- | --- | | MarkDown=MarkDown4 | -2336.799791 | | --- | --- | | MarkDown=MarkDown5 | 215.060616 年 | | --- | --- | | MarkDown=No Markdown | 1102.245760 號 | | --- | --- | | Temperature | -330.912587 號 | | --- | --- | | Unemployment | 1205.564331 年 | | --- | --- | | Intercept | 29723.135729 個 | | --- | --- | 我們可以看到，即使我們使用一個熱編碼列來擬合線性回歸模型，燃油價格、溫度和失業率的權重也與以前的值非常相似。與截距項相比，所有權重都很小，這意味著大多數變量仍然與實際銷售額略有關聯。事實上，`IsHoliday`變量的模型權重非常低，以至于在預測日期是否為假日時幾乎沒有區別。盡管一些`MarkDown`權重相當大，但許多降價事件在數據集中只出現幾次。 ``` walmart['MarkDown'].value_counts() ``` ``` No Markdown 92 MarkDown1 25 MarkDown2 13 MarkDown5 9 MarkDown4 2 MarkDown3 2 Name: MarkDown, dtype: int64 ``` 這表明我們可能需要收集更多的數據，以便模型更好地利用降價事件對銷售額的影響。（實際上，這里顯示的數據集是沃爾瑪發布的[大得多的數據集](https://www.kaggle.com/c/walmart-recruiting-store-sales-forecasting)的一個子集。使用整個數據集而不是一個子集訓練模型將是一個有用的練習。） ## 摘要[?](#Summary) 我們已經學會了使用一種熱編碼，這是一種對分類數據進行線性回歸的有用技術。盡管在這個特定的例子中，轉換對我們的模型沒有太大的影響，但在實際中，這種技術在處理分類數據時得到了廣泛的應用。一個熱編碼還說明了特征工程的一般原理，它采用原始數據矩陣，并將其轉換為一個潛在的更有用的矩陣。