# Logistic 模型的損失函數 > 原文：[https://www.textbook.ds100.org/ch/17/classification_cost.html](https://www.textbook.ds100.org/ch/17/classification_cost.html) ``` # HIDDEN # Clear previously defined variables %reset -f # Set directory for data loading to work properly import os os.chdir(os.path.expanduser('~/notebooks/17')) ``` ``` # HIDDEN import warnings # Ignore numpy dtype warnings. These warnings are caused by an interaction # between numpy and Cython and can be safely ignored. # Reference: https://stackoverflow.com/a/40846742 warnings.filterwarnings("ignore", message="numpy.dtype size changed") warnings.filterwarnings("ignore", message="numpy.ufunc size changed") import numpy as np import matplotlib.pyplot as plt import pandas as pd import seaborn as sns %matplotlib inline import ipywidgets as widgets from ipywidgets import interact, interactive, fixed, interact_manual import nbinteract as nbi sns.set() sns.set_context('talk') np.set_printoptions(threshold=20, precision=2, suppress=True) pd.options.display.max_rows = 7 pd.options.display.max_columns = 8 pd.set_option('precision', 2) # This option stops scientific notation for pandas # pd.set_option('display.float_format', '{:.2f}'.format) ``` ``` # HIDDEN def df_interact(df, nrows=7, ncols=7): ''' Outputs sliders that show rows and columns of df ''' def peek(row=0, col=0): return df.iloc[row:row + nrows, col:col + ncols] if len(df.columns) <= ncols: interact(peek, row=(0, len(df) - nrows, nrows), col=fixed(0)) else: interact(peek, row=(0, len(df) - nrows, nrows), col=(0, len(df.columns) - ncols)) print('({} rows, {} columns) total'.format(df.shape[0], df.shape[1])) ``` ``` # HIDDEN lebron = pd.read_csv('lebron.csv') ``` 我們定義了概率的回歸模型，邏輯模型： $$ \begin{aligned} f_\hat{\boldsymbol{\theta}} (\textbf{x}) = \sigma(\hat{\boldsymbol{\theta}} \cdot \textbf{x}) \end{aligned} $$ 與線性回歸模型一樣，該模型也有參數$\Hat \BoldSymbol \Theta$，這是一個向量，它為每個$\textbf x 的特征包含一個參數。我們現在解決的問題是為這個模型定義一個損失函數，它允許我們將模型的參數與數據相匹配。 直觀地說，我們希望模型的預測與數據盡可能接近。下面，我們用每球與籃筐之間的距離，重現了勒布朗在 2017 年 NBA 季后賽中的投籃嘗試。這些點在 Y 軸上抖動以減輕過度繪制。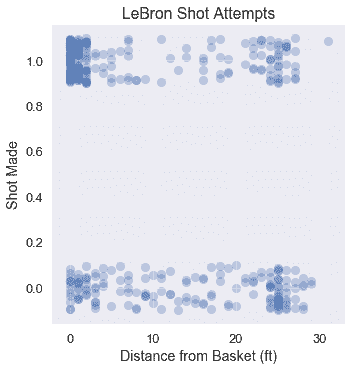 ``` # HIDDEN np.random.seed(42) sns.lmplot(x='shot_distance', y='shot_made', data=lebron, fit_reg=False, ci=False, y_jitter=0.1, scatter_kws={'alpha': 0.3}) plt.title('LeBron Shot Attempts') plt.xlabel('Distance from Basket (ft)') plt.ylabel('Shot Made'); ```  注意到籃筐附近的大量投籃和籃筐遠處的較小的錯失投籃，我們預計此數據上的邏輯模型可能如下所示： ``` # HIDDEN from scipy.special import expit np.random.seed(42) sns.lmplot(x='shot_distance', y='shot_made', data=lebron, fit_reg=False, ci=False, y_jitter=0.1, scatter_kws={'alpha': 0.3}) xs = np.linspace(-2, 32, 100) ys = expit(-0.15 * (xs - 15)) plt.plot(xs, ys, c='r', label='Logistic model') plt.title('Possible logistic model fit') plt.xlabel('Distance from Basket (ft)') plt.ylabel('Shot Made'); ```  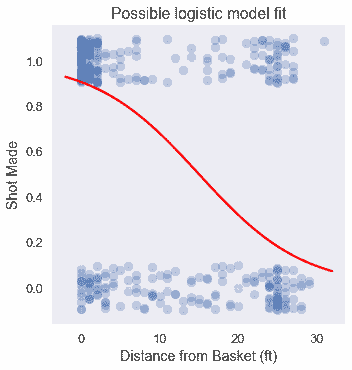雖然我們可以像線性回歸那樣使用均方誤差損失函數，但對于一個邏輯模型來說，它是非凸的，因此難以優化。 ## 交叉熵損失 我們使用**交叉熵損失**來代替均方誤差。讓$\textbf x$表示 P$輸入數據矩陣的$n 倍，$\textbf y$表示觀測數據值的矢量，$f \boldsymbol \theta（\textbf x）$表示邏輯模型。$\BoldSymbol \Theta$包含當前參數值。使用此符號，平均交叉熵損失定義為： $$ \begin{aligned} L(\boldsymbol{\theta}, \textbf{X}, \textbf{y}) = \frac{1}{n} \sum_i \left(- y_i \ln (f_\boldsymbol{\theta}(\textbf{X}_i)) - (1 - y_i) \ln (1 - f_\boldsymbol{\theta}(\textbf{X}_i) \right) \end{aligned} $$ 您可以觀察到，像往常一樣，我們對數據集中的每個點取平均損失。上述總和中的內部表達式表示一個數據點的損失$（\textbf x u i，y_i）$： $$ \begin{aligned} \ell(\boldsymbol{\theta}, \textbf{X}_i, y_i) = - y_i \ln (f_\boldsymbol{\theta}(\textbf{X}_i)) - (1 - y_i) \ln (1 - f_\boldsymbol{\theta}(\textbf{X}_i) ) \end{aligned} $$ 回想一下，數據集中的每個$y_i$都是 0 或 1。如果 Y_i=0 美元，損失的第一項為零。如果 Y_i=1 美元，損失中的第二項為零。因此，對于數據集中的每個點，只有一個交叉熵損失項會導致整體損失。 假設$y_i=0$和我們的預測概率$f_uuBoldSymbol \theta（\textbf x _i）=0$我們的模型是完全正確的。這一點的損失將是： $$ \begin{aligned} \ell(\boldsymbol{\theta}, \textbf{X}_i, y_i) &= - y_i \ln (f_\boldsymbol{\theta}(\textbf{X}_i)) - (1 - y_i) \ln (1 - f_\boldsymbol{\theta}(\textbf{X}_i) ) \\ &= - 0 - (1 - 0) \ln (1 - 0 ) \\ &= - \ln (1) \\ &= 0 \end{aligned} $$ 正如預期的那樣，正確預測的損失是 0 美元。您可以驗證預測概率與真實值越遠，損失越大。 最大限度地減少總體交叉熵損失需要模型$F_BoldSymbol \Theta（\textbf_x）$來做出最準確的預測。方便的是，該損失函數是凸的，使得梯度下降成為一種有用的優化選擇。 ## 交叉熵損失梯度 為了對模型的交叉熵損失進行梯度下降，必須計算損失函數的梯度。首先，我們計算 sigmoid 函數的導數，因為我們將在梯度計算中使用它。 $$ \begin{aligned} \sigma(t) &= \frac{1}{1 + e^{-t}} \\ \sigma'(t) &= \frac{e^{-t}}{(1 + e^{-t})^2} \\ \sigma'(t) &= \frac{1}{1 + e^{-t}} \cdot \left(1 - \frac{1}{1 + e^{-t}} \right) \\ \sigma'(t) &= \sigma(t) (1 - \sigma(t)) \end{aligned} $$ 乙狀結腸功能的導數可以方便地用乙狀結腸功能本身來表示。 簡而言之，我們定義了$\sigma（\textbf x u i）=\sigma（\textbf x u i \cdot \boldsymbol \theta）$。我們很快就需要.\sigma i$相對于向量.\boldsymbol \theta 的梯度，因此我們現在將使用鏈規則的直接應用來推導它。 $$ \begin{aligned} \nabla_{\boldsymbol{\theta}} \sigma_i &= \nabla_{\boldsymbol{\theta}} \sigma(\textbf{X}_i \cdot \boldsymbol{\theta}) \\ &= \sigma(\textbf{X}_i \cdot \boldsymbol{\theta}) (1 - \sigma(\textbf{X}_i \cdot \boldsymbol{\theta})) \nabla_{\boldsymbol{\theta}} (\textbf{X}_i \cdot \boldsymbol{\theta}) \\ &= \sigma_i (1 - \sigma_i) \textbf{X}_i \end{aligned} $$ 現在，我們推導出交叉熵損失相對于模型參數$\BoldSymbol \Theta 的梯度。在下面的推導中，我們讓$\sigma_i=f_ \boldsymbol \theta（\textbf x（\textbf x u i \cdot \boldsymbol \theta）$。 $$ \begin{aligned} L(\boldsymbol{\theta}, \textbf{X}, \textbf{y}) &= \frac{1}{n} \sum_i \left(- y_i \ln (f_\boldsymbol{\theta}(\textbf{X}_i)) - (1 - y_i) \ln (1 - f_\boldsymbol{\theta}(\textbf{X}_i) \right) \\ &= \frac{1}{n} \sum_i \left(- y_i \ln \sigma_i - (1 - y_i) \ln (1 - \sigma_i) \right) \\ \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}, \textbf{X}, \textbf{y}) &= \frac{1}{n} \sum_i \left( - \frac{y_i}{\sigma_i} \nabla_{\boldsymbol{\theta}} \sigma_i + \frac{1 - y_i}{1 - \sigma_i} \nabla_{\boldsymbol{\theta}} \sigma_i \right) \\ &= - \frac{1}{n} \sum_i \left( \frac{y_i}{\sigma_i} - \frac{1 - y_i}{1 - \sigma_i} \right) \nabla_{\boldsymbol{\theta}} \sigma_i \\ &= - \frac{1}{n} \sum_i \left( \frac{y_i}{\sigma_i} - \frac{1 - y_i}{1 - \sigma_i} \right) \sigma_i (1 - \sigma_i) \textbf{X}_i \\ &= - \frac{1}{n} \sum_i \left( y_i - \sigma_i \right) \textbf{X}_i \\ \end{aligned} $$ 令人驚訝的簡單梯度表達式允許我們使用梯度下降將邏輯模型擬合到交叉熵損失： $$ \hat{\boldsymbol{\theta}} = \displaystyle\arg \min_{\substack{\boldsymbol{\theta}}} L(\boldsymbol{\theta}, \textbf{X}, \textbf{y})$$ 第 17.6 節探討了批量、隨機和小批量梯度下降的更新公式。 ## 摘要[?](#Summary) 由于交叉熵損失函數是凸的，因此我們使用梯度下降將其最小化，以使邏輯模型適合數據。我們現在有了邏輯回歸的必要組成部分：模型、損失函數和最小化過程。在第 17.5 節中，我們更詳細地了解了為什么我們使用平均交叉熵損失進行邏輯回歸。