# 預測小費金額 > 原文：[https://www.bookbookmark.ds100.org/ch/13/linear_tips.html](https://www.bookbookmark.ds100.org/ch/13/linear_tips.html) ``` # HIDDEN # Clear previously defined variables %reset -f # Set directory for data loading to work properly import os os.chdir(os.path.expanduser('~/notebooks/13')) ``` ``` # HIDDEN import warnings # Ignore numpy dtype warnings. These warnings are caused by an interaction # between numpy and Cython and can be safely ignored. # Reference: https://stackoverflow.com/a/40846742 warnings.filterwarnings("ignore", message="numpy.dtype size changed") warnings.filterwarnings("ignore", message="numpy.ufunc size changed") import numpy as np import matplotlib.pyplot as plt import pandas as pd import seaborn as sns %matplotlib inline import ipywidgets as widgets from ipywidgets import interact, interactive, fixed, interact_manual import nbinteract as nbi sns.set() sns.set_context('talk') np.set_printoptions(threshold=20, precision=2, suppress=True) pd.options.display.max_rows = 7 pd.options.display.max_columns = 8 pd.set_option('precision', 2) # This option stops scientific notation for pandas # pd.set_option('display.float_format', '{:.2f}'.format) ``` 以前，我們使用一個數據集，該數據集包含一個服務生一周內提供的每個表的一行。我們的服務員收集了這些數據，以便預測他將來從一張桌子上能收到的小費金額。 ``` tips = sns.load_dataset('tips') tips.head() ``` | | 賬單合計 | 提示 | 性別 | 吸煙者 | 白天 | 時間 | 大小 | | --- | --- | --- | --- | --- | --- | --- | --- | | 零 | 十六點九九 | 1.01 年 | 女性 | 不 | 太陽 | 晚餐 | 二 | | --- | --- | --- | --- | --- | --- | --- | --- | | 1 個 | 十點三四 | 一點六六 | 男性 | No | Sun | Dinner | 三 | | --- | --- | --- | --- | --- | --- | --- | --- | | 二 | 二十一點零一 | 3.50 美元 | Male | No | Sun | Dinner | 3 | | --- | --- | --- | --- | --- | --- | --- | --- | | 三 | 二十三點六八 | 三點三一 | Male | No | Sun | Dinner | 2 | | --- | --- | --- | --- | --- | --- | --- | --- | | 四 | 二十四點五九 | 三點六一 | Female | No | Sun | Dinner | 四 | | --- | --- | --- | --- | --- | --- | --- | --- | ``` sns.distplot(tips['tip'], bins=25); ```  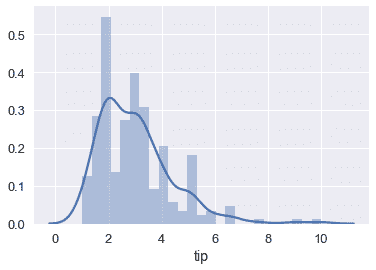如前所述，如果我們選擇一個常數模型和均方誤差成本，我們的模型將預測尖端數量的平均值： ``` np.mean(tips['tip']) ``` ``` 2.9982786885245902 ``` 這意味著，如果一個新的聚會點了一頓飯，服務員問我們他可能會收到多少小費，我們會說“大約 3 美元”，不管桌子有多大，或者他們的總帳單有多少。 然而，觀察數據集中的其他變量，我們發現如果我們將它們合并到我們的模型中，我們可能能夠做出更準確的預測。例如，下面的小費金額與總賬單的圖表顯示了一個正關聯。 ``` # HIDDEN sns.lmplot(x='total_bill', y='tip', data=tips, fit_reg=False) plt.title('Tip amount vs. 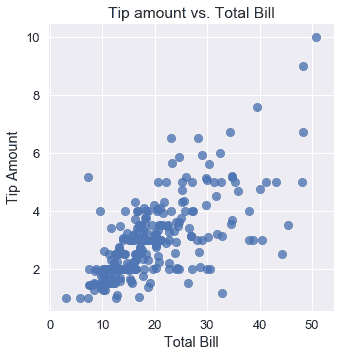Total Bill') plt.xlabel('Total Bill') plt.ylabel('Tip Amount'); ```  雖然小費的平均金額是 3 美元，但如果一張桌子訂購價值 40 美元的食物，我們肯定會期望服務員收到超過 3 美元的小費。因此，我們希望改變我們的模型，使其基于數據集中的變量進行預測，而不是盲目地預測平均尖端量。為此，我們使用線性模型而不是常量模型。 讓我們簡要回顧一下我們當前的建模和估計工具箱，并定義一些新的表示法，以便更好地表示線性模型所具有的額外復雜性。 ## 定義簡單線性模型 我們有興趣根據一張表的總帳單來預測小費金額。讓$Y$代表小費金額，這是我們試圖預測的變量。讓$x$代表總賬單，我們將其合并用于預測的變量。 我們定義了一個線性模型$f_ \boldSymbol\theta^*$依賴于$x$： $$ f_\boldsymbol\theta^* (x) = \theta_1^* x + \theta_0^* $$ 我們將$f_u \boldsymbol\theta^*（x）$作為生成數據的基礎函數。 $F_u \boldsymbol\theta^*（x）$假設實際上，$Y$與$X$具有完全線性關系。然而，由于一些隨機噪聲，我們的觀測數據并沒有完全沿著直線移動。在數學上，我們通過添加一個噪聲項來解釋這一點： $$ y = f_\boldsymbol\theta^* (x) + \epsilon $$ 如果假設$Y$與$X$的關系是完全線性的，并且我們能夠以某種方式找到$\theta_1^*$和$\theta_0^*$的精確值，并且我們神奇地沒有隨機噪聲，那么我們就能夠完美地預測服務員為所有桌子得到的小費的數量，永遠。當然，在實踐中我們不能完全滿足這些標準中的任何一個。相反，我們將使用我們的數據集來估計$\theta_1^*$和$\theta_0^*$以使我們的預測盡可能準確。 ### 線性模型估計 由于我們找不到確切的$\Theta_1^*$和$\Theta_0^*$數據，因此我們假設數據集近似于我們的總體，并使用數據集來估計這些參數。我們用$\theta_$和$\theta_$表示我們的估計，用$\hat \theta_ 和$\hat \theta_ 表示我們的擬合估計，我們的模型為： $$ f_\boldsymbol\theta (x) = \theta_1 x + \theta_0 $$ 有時，您會看到$H（x）$而不是$F \BoldSymbol\Theta（x）$的書寫，$H$代表假設，因為$F \BoldSymbol\Theta（x）$是我們對$F \BoldSymbol\Theta ^*（x）$的假設。 為了確定$\hat \theta 1 和$\hat \theta 0 美元，我們選擇了一個成本函數，并使用梯度下降將其最小化。