# 正則化直覺 > 原文：[https://www.textbook.ds100.org/ch/16/reg_invituation.html](https://www.textbook.ds100.org/ch/16/reg_invituation.html) ``` # HIDDEN # Clear previously defined variables %reset -f # Set directory for data loading to work properly import os os.chdir(os.path.expanduser('~/notebooks/16')) ``` ``` # HIDDEN import warnings # Ignore numpy dtype warnings. These warnings are caused by an interaction # between numpy and Cython and can be safely ignored. # Reference: https://stackoverflow.com/a/40846742 warnings.filterwarnings("ignore", message="numpy.dtype size changed") warnings.filterwarnings("ignore", message="numpy.ufunc size changed") import numpy as np import matplotlib.pyplot as plt import pandas as pd import seaborn as sns %matplotlib inline import ipywidgets as widgets from ipywidgets import interact, interactive, fixed, interact_manual import nbinteract as nbi sns.set() sns.set_context('talk') np.set_printoptions(threshold=20, precision=2, suppress=True) pd.options.display.max_rows = 7 pd.options.display.max_columns = 8 pd.set_option('precision', 2) # This option stops scientific notation for pandas # pd.set_option('display.float_format', '{:.2f}'.format) ``` ``` # HIDDEN def df_interact(df, nrows=7, ncols=7): ''' Outputs sliders that show rows and columns of df ''' def peek(row=0, col=0): return df.iloc[row:row + nrows, col:col + ncols] if len(df.columns) <= ncols: interact(peek, row=(0, len(df) - nrows, nrows), col=fixed(0)) else: interact(peek, row=(0, len(df) - nrows, nrows), col=(0, len(df.columns) - ncols)) print('({} rows, {} columns) total'.format(df.shape[0], df.shape[1])) ``` ``` # HIDDEN df = pd.read_csv('water_large.csv') ``` ``` # HIDDEN from collections import namedtuple Curve = namedtuple('Curve', ['xs', 'ys']) def flatten(seq): return [item for subseq in seq for item in subseq] def make_curve(clf, x_start=-50, x_end=50): xs = np.linspace(x_start, x_end, num=100) ys = clf.predict(xs.reshape(-1, 1)) return Curve(xs, ys) def plot_data(df=df, ax=plt, **kwargs): ax.scatter(df.iloc[:, 0], df.iloc[:, 1], s=50, **kwargs) def plot_curve(curve, ax=plt, **kwargs): ax.plot(curve.xs, curve.ys, **kwargs) def plot_curves(curves, cols=2): rows = int(np.ceil(len(curves) / cols)) fig, axes = plt.subplots(rows, cols, figsize=(10, 8), sharex=True, sharey=True) for ax, curve, deg in zip(flatten(axes), curves, degrees): plot_data(ax=ax, label='Training data') plot_curve(curve, ax=ax, label=f'Deg {deg} poly') ax.set_ylim(-5e10, 170e10) ax.legend() # add a big axes, hide frame fig.add_subplot(111, frameon=False) # hide tick and tick label of the big axes plt.tick_params(labelcolor='none', top='off', bottom='off', left='off', right='off') plt.grid(False) plt.title('Polynomial Regression') plt.xlabel('Water Level Change (m)') plt.ylabel('Water Flow (Liters)') plt.tight_layout() def print_coef(clf): reg = clf.named_steps['reg'] print(reg.intercept_) print(reg.coef_) ``` ``` # HIDDEN X = df.iloc[:, [0]].as_matrix() y = df.iloc[:, 1].as_matrix() degrees = [1, 2, 8, 12] clfs = [Pipeline([('poly', PolynomialFeatures(degree=deg, include_bias=False)), ('reg', LinearRegression())]) .fit(X, y) for deg in degrees] curves = [make_curve(clf) for clf in clfs] ridge_clfs = [Pipeline([('poly', PolynomialFeatures(degree=deg, include_bias=False)), ('reg', Ridge(alpha=0.1, normalize=True))]) .fit(X, y) for deg in degrees] ridge_curves = [make_curve(clf) for clf in ridge_clfs] ``` 我們從一個例子開始討論正則化，這個例子說明了正則化的重要性。 ## 大壩數據 以下數據集以升為單位記錄某一天從大壩流出的水量，以米為單位記錄該天水位的變化量。 ``` # HIDDEN df ``` | | 水位變化 | 水流 | | --- | --- | --- | | 零 | -15.936758 | 6.042233E+10 號 | | --- | --- | --- | | 1 個 | -29.152979 年 | 3.321490E+10 型 | | --- | --- | --- | | 二 | 36.189549 年 | 9.727064E+11 號 | | --- | --- | --- | | …… | …… | ... | | --- | --- | --- | | 20 個 | 7.085480 | 2.363520E+11 號 | | --- | --- | --- | | 21 歲 | 46.282369 年 | 1.494256E+12 | | --- | --- | --- | | 二十二 | 14.612289 年 | 3.781463E+11 號 | | --- | --- | --- | 23 行×2 列 繪制這些數據表明，隨著水位變得更為積極，水流呈上升趨勢。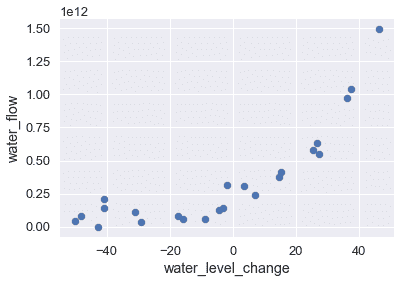 ``` # HIDDEN df.plot.scatter(0, 1, s=50); ```  為了建立這個模式，我們可以使用最小二乘線性回歸模型。我們在下面的圖表中顯示數據和模型的預測。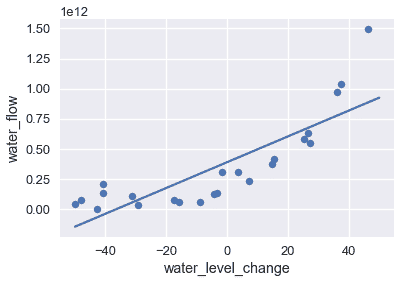 ``` # HIDDEN df.plot.scatter(0, 1, s=50); plot_curve(curves[0]) ```  可視化結果表明，該模型不捕獲數據中的模式，模型具有很高的偏差。正如我們之前所做的，我們可以嘗試通過在數據中添加多項式特征來解決這個問題。我們添加 2、8 和 12 度的多項式特征；下表顯示了訓練數據和每個模型的預測。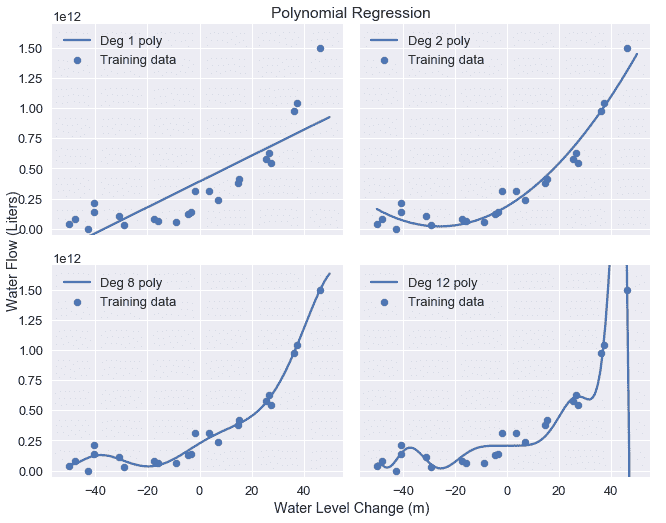 ``` # HIDDEN plot_curves(curves) ```  正如預期的那樣，12 次多項式很好地匹配訓練數據，但似乎也適合由噪聲引起的數據中的偽模式。這提供了另一個關于偏差-方差權衡的說明：線性模型具有高偏差和低方差，而度 12 多項式具有低偏差但高方差。 ## 檢查系數[?](#Examining-Coefficients) 檢驗 12 次多項式模型的系數，發現該模型根據以下公式進行預測： $$ 207097470825 + 1.8x + 482.6x^2 + 601.5x^3 + 872.8x^4 + 150486.6x^5 \\ + 2156.7x^6 - 307.2x^7 - 4.6x^8 + 0.2x^9 + 0.003x^{10} - 0.00005x^{11} + 0x^{12} $$ 其中$x$是當天的水位變化。 模型的系數相當大，尤其是對模型方差有顯著貢獻的更高階項（例如，x^5$和 x^6$）。 ## 懲罰參數[?](#Penalizing-Parameters) 回想一下，我們的線性模型根據以下內容進行預測，其中$\theta$是模型權重，$x$是特征向量： $$ f_\hat{\theta}(x) = \hat{\theta} \cdot x $$ 為了適應我們的模型，我們將均方誤差成本函數最小化，其中$x$用于表示數據矩陣，$y$用于觀察結果： $$ \begin{aligned} L(\hat{\theta}, X, y) &= \frac{1}{n} \sum_{i}(y_i - f_\hat{\theta} (X_i))^2\\ \end{aligned} $$ 為了將上述成本降到最低，我們調整$\hat \theta$直到找到最佳的權重組合，而不管權重本身有多大。然而，我們發現更復雜特征的權重越大，模型方差越大。如果我們可以改變成本函數來懲罰較大的權重值，那么得到的模型將具有較低的方差。我們用正規化來增加這個懲罰。