# 隨機梯度下降法 > 原文：[https://www.bookbookmark.ds100.org/ch/11/gradient_randomatic.html](https://www.bookbookmark.ds100.org/ch/11/gradient_randomatic.html) ``` # HIDDEN # Clear previously defined variables %reset -f # Set directory for data loading to work properly import os os.chdir(os.path.expanduser('~/notebooks/11')) ``` ``` # HIDDEN import warnings # Ignore numpy dtype warnings. These warnings are caused by an interaction # between numpy and Cython and can be safely ignored. # Reference: https://stackoverflow.com/a/40846742 warnings.filterwarnings("ignore", message="numpy.dtype size changed") warnings.filterwarnings("ignore", message="numpy.ufunc size changed") import numpy as np import matplotlib.pyplot as plt import pandas as pd import seaborn as sns %matplotlib inline import ipywidgets as widgets from ipywidgets import interact, interactive, fixed, interact_manual import nbinteract as nbi sns.set() sns.set_context('talk') np.set_printoptions(threshold=20, precision=2, suppress=True) pd.options.display.max_rows = 7 pd.options.display.max_columns = 8 pd.set_option('precision', 2) # This option stops scientific notation for pandas # pd.set_option('display.float_format', '{:.2f}'.format) ``` 在本節中，我們將討論對梯度下降的修改，這使得它對大型數據集更有用。修改后的算法稱為**隨機梯度下降**。 回憶梯度下降使用所選損失函數的梯度更新模型參數$\theta$。具體來說，我們使用了這個梯度更新公式： $$ {\theta}^{(t+1)} = \theta^{(t)} - \alpha \cdot \nabla_{\theta} L(\theta^{(t)}, \textbf{y}) $$ 在這個方程中： * $\theta^（t）$是我們在第$t$th 次迭代時對$\theta^*$的當前估計值。 * $\alpha$是學習率 * $是損失函數的梯度 * 我們計算下一個估計值$\theta^（t+1）$減去以\theta^（t）（t）計算的$\alpha$和$\nabla \theta l（\theta，textbf y）$的乘積。$ ### 批梯度下降的限制 在上面的表達式中，我們使用損失函數$\ell（\theta，y_i）$的平均梯度（使用**整個數據集**計算$\nabla \theta（\theta，y）$的值。換句話說，每次更新$\theta$時，我們都會作為一個完整的批處理查詢數據集中的所有其他點。因此，上面的梯度更新規則通常被稱為**批梯度下降**。 不幸的是，我們經常使用大型數據集。雖然批量梯度下降通常會在相對較少的迭代中找到一個最優的$\theta$，但是如果訓練集包含多個點，則每次迭代都需要很長的時間來計算。 ### 隨機梯度下降 為了避免在整個訓練集中計算梯度的困難，隨機梯度下降使用單個隨機選擇的數據點來近似整體梯度。由于觀測是隨機選擇的，我們期望在每個單獨觀測中使用梯度最終會收斂到與批梯度下降相同的參數。 再次考慮批次梯度下降的公式： $$ {\theta}^{(t+1)} = \theta^{(t)} - \alpha \cdot \nabla_{\theta} L(\theta^{(t)}, \textbf{y}) $$ 在這個公式中，我們有一個術語“$\nabla \theta l（\theta ^（t）、\textbf y）”$，培訓集中所有點的損失函數平均梯度。即： $$ \begin{aligned} \nabla_{\theta} L(\theta^{(t)}, \textbf{y}) &= \frac{1}{n} \sum_{i=1}^{n} \nabla_{\theta} \ell(\theta^{(t)}, y_i) \end{aligned} $$ 其中，$\ell（\theta，y_i）$是訓練集中某一點的損失。為了進行隨機梯度下降，我們只需將平均梯度替換為單點的梯度。隨機梯度下降的梯度更新公式為： $$ {\theta}^{(t+1)} = \theta^{(t)} - \alpha \cdot \nabla_{\theta} \ell(\theta^{(t)}, y_i) $$ 在這個公式中，$Y I$是從$\textbf Y$中隨機選擇的。注意，隨機選擇點對隨機梯度下降的成功至關重要！如果不隨機選取點，隨機梯度下降可能比批量梯度下降產生更差的結果。 我們最常用的方法是隨機梯度下降，通過改變數據點的排列順序，使用每個點的排列順序，直到完成一個完整的訓練數據。如果算法沒有收斂，我們就重新組合點，并運行另一個數據傳遞。隨機梯度下降的每個**迭代**都會查看一個數據點；每個完整的數據傳遞都稱為**epoch**。 #### 使用 MSE 損耗[?](#Using-the-MSE-Loss) 作為一個例子，我們推導了均方損失的隨機梯度下降更新公式。回顧平均平方損失的定義： $$ \begin{aligned} L(\theta, \textbf{y}) &= \frac{1}{n} \sum_{i = 1}^{n}(y_i - \theta)^2 \end{aligned} $$ 考慮到$\theta$的梯度，我們有： $$ \begin{aligned} \nabla_{\theta} L(\theta, \textbf{y}) &= \frac{1}{n} \sum_{i = 1}^{n} -2(y_i - \theta) \end{aligned} $$ 因為上面的公式給出了數據集中所有點的平均梯度損失，所以單個點的梯度損失只是被平均的公式的一部分： $$ \begin{aligned} \nabla_{\theta} \ell(\theta, y_i) &= -2(y_i - \theta) \end{aligned} $$ 因此，MSE 損失的批梯度更新規則為： $$ \begin{aligned} {\theta}^{(t+1)} = \theta^{(t)} - \alpha \cdot \left( \frac{1}{n} \sum_{i = 1}^{n} -2(y_i - \theta) \right) \end{aligned} $$ 隨機梯度更新規則為： $$ \begin{aligned} {\theta}^{(t+1)} = \theta^{(t)} - \alpha \cdot \left( -2(y_i - \theta) \right) \end{aligned} $$ ### 隨機梯度下降行為 由于隨機下降一次只檢查一個數據點，因此它可能會比批梯度下降的更新更準確地更新$\theta$然而，由于隨機梯度下降計算更新比批梯度下降快得多，隨機梯度下降可以在批梯度下降完成單個更新時，朝著最優的$\theta$取得顯著進展。 在下面的圖片中，我們使用批梯度下降顯示對$\theta$的連續更新。圖中最暗的區域對應于我們訓練數據中的最優值$\theta$，$\hat \theta$。 （此圖從技術上顯示了一個具有兩個參數的模型，但更重要的是，批梯度下降總是朝著$\hat \theta 的方向邁出一步。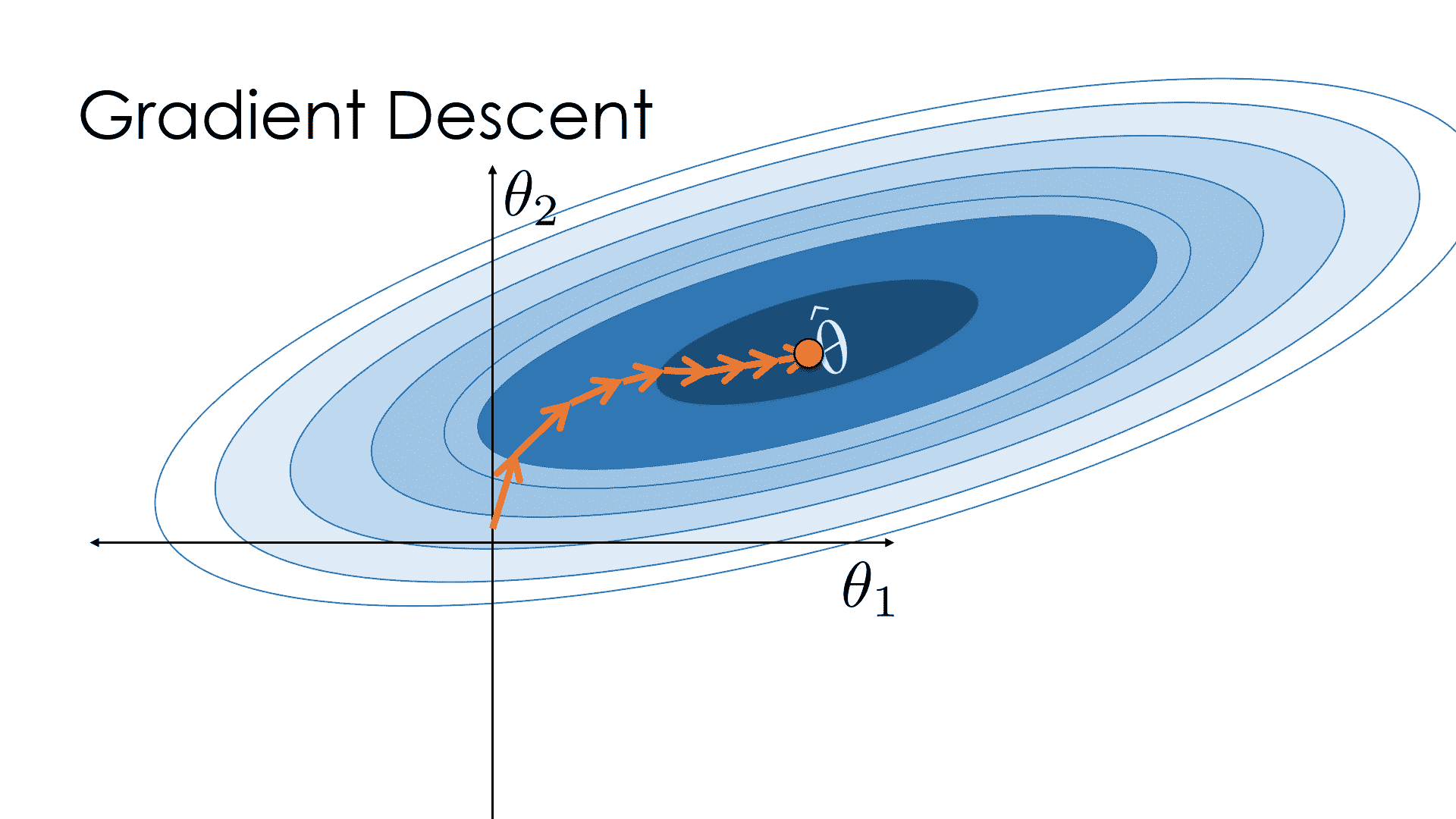）  另一方面，隨機梯度下降通常會從$\hat \theta$開始逐步下降！然而，由于它使更新更頻繁，所以它通常比批梯度下降更快地收斂。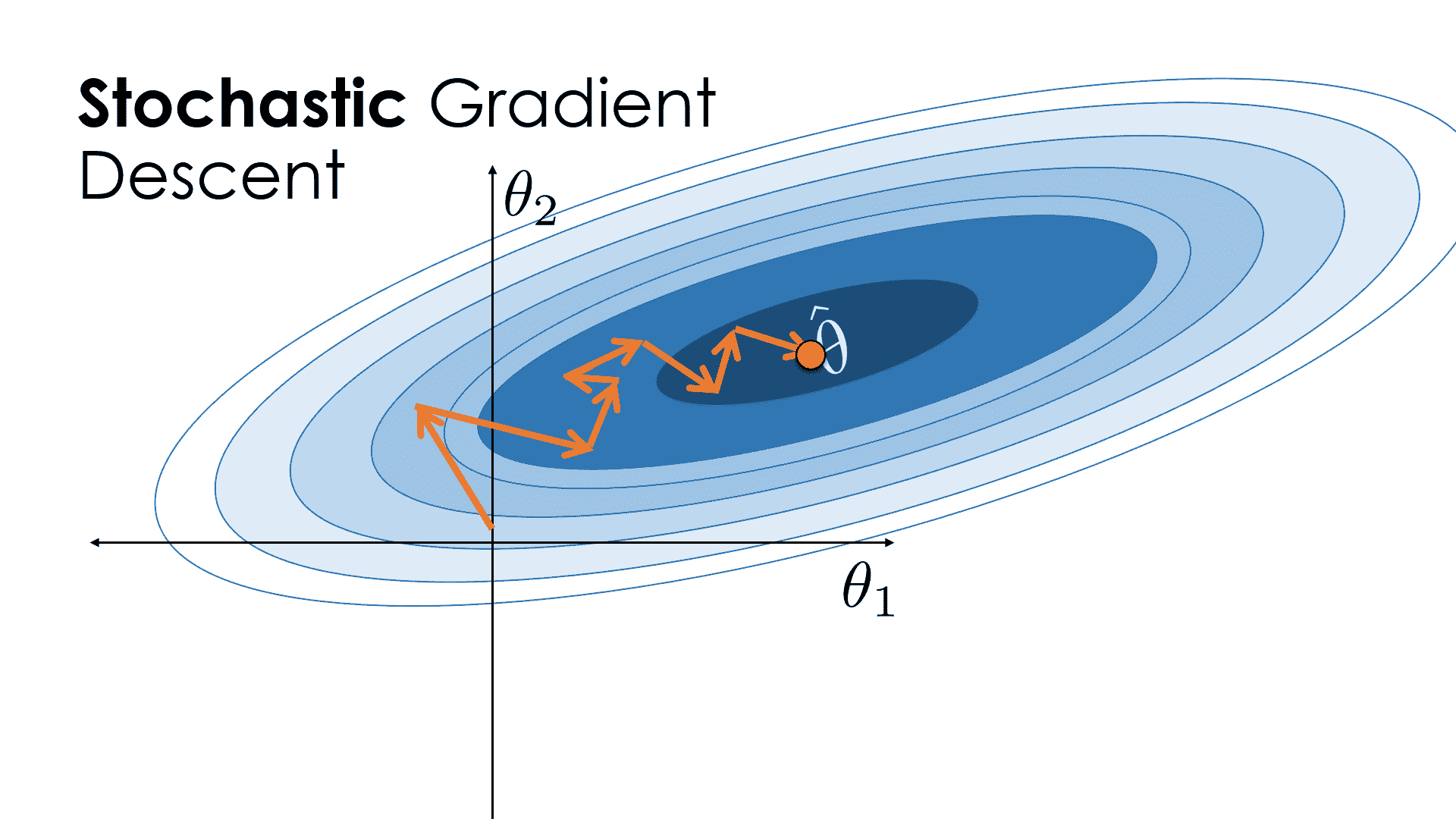  ### 定義隨機梯度下降函數 正如我們之前對批梯度下降所做的那樣，我們定義了一個函數來計算損失函數的隨機梯度下降。它將類似于我們的`minimize`函數，但我們需要在每次迭代中實現一個觀測的隨機選擇。 ``` def minimize_sgd(loss_fn, grad_loss_fn, dataset, alpha=0.2): """ Uses stochastic gradient descent to minimize loss_fn. Returns the minimizing value of theta once theta changes less than 0.001 between iterations. """ NUM_OBS = len(dataset) theta = 0 np.random.shuffle(dataset) while True: for i in range(0, NUM_OBS, 1): rand_obs = dataset[i] gradient = grad_loss_fn(theta, rand_obs) new_theta = theta - alpha * gradient if abs(new_theta - theta) < 0.001: return new_theta theta = new_theta np.random.shuffle(dataset) ``` ### 小批量梯度下降 **小批量梯度下降**通過增加我們在每次迭代中選擇的觀測次數，實現了批量梯度下降和隨機梯度下降之間的平衡。在小批量梯度下降中，我們對每個梯度更新使用一些數據點，而不是單個點。 我們利用損失函數梯度的平均值來估計交叉熵損失的真實梯度。如果$\mathcal b$是我們從$n$觀察值中隨機抽樣的一小批數據點，則以下近似值成立。 $$ \nabla_\theta L(\theta, \textbf{y}) \approx \frac{1}{|\mathcal{B}|} \sum_{i\in\mathcal{B}}\nabla_{\theta}\ell(\theta, y_i) $$ 與隨機梯度下降一樣，我們通過改變訓練數據的格式和通過迭代隨機數據選擇小批量來執行小批量梯度下降。在每個時代之后，我們重新洗牌我們的數據并選擇新的小批量。 雖然我們已經在這本教科書中區分了隨機和小批量梯度下降，但隨機梯度下降有時被用作一個涵蓋選擇任何大小的小批量的總稱。 #### 選擇小批量大小[?](#Selecting-the-Mini-Batch-Size) 在某些計算機中的圖形處理單元（GPU）芯片上運行時，最小批量梯度下降最為理想。由于這些硬件類型的計算可以并行執行，因此使用小批量可以在不增加計算時間的情況下提高梯度的精度。根據 GPU 的內存，小批量通常設置在 10 到 100 個觀察值之間。 ### 為小批量梯度下降定義函數 用于小批量梯度下降的函數要求能夠選擇批量大小。下面是實現此功能的函數。 ``` def minimize_mini_batch(loss_fn, grad_loss_fn, dataset, minibatch_size, alpha=0.2): """ Uses mini-batch gradient descent to minimize loss_fn. Returns the minimizing value of theta once theta changes less than 0.001 between iterations. """ NUM_OBS = len(dataset) assert minibatch_size < NUM_OBS theta = 0 np.random.shuffle(dataset) while True: for i in range(0, NUM_OBS, minibatch_size): mini_batch = dataset[i:i+minibatch_size] gradient = grad_loss_fn(theta, mini_batch) new_theta = theta - alpha * gradient if abs(new_theta - theta) < 0.001: return new_theta theta = new_theta np.random.shuffle(dataset) ``` ## 摘要[?](#Summary) 我們使用批梯度下降迭代改進模型參數，直到模型達到最小損失。由于批量梯度下降是大數據集難以計算的問題，我們經常使用隨機梯度下降來擬合模型。在使用 GPU 時，在相同的計算代價下，小批量梯度下降比隨機梯度下降收斂得更快。對于大型數據集，隨機梯度下降和小批量梯度下降通常比批量梯度下降更為可取，因為它們的計算速度更快。