# 隨機變量 > 原文：[https://www.bookbookmark.ds100.org/ch/12/prob_random_vars.html](https://www.bookbookmark.ds100.org/ch/12/prob_random_vars.html) ``` # HIDDEN # Clear previously defined variables %reset -f # Set directory for data loading to work properly import os os.chdir(os.path.expanduser('~/notebooks/12')) ``` ``` # HIDDEN import warnings # Ignore numpy dtype warnings. These warnings are caused by an interaction # between numpy and Cython and can be safely ignored. # Reference: https://stackoverflow.com/a/40846742 warnings.filterwarnings("ignore", message="numpy.dtype size changed") warnings.filterwarnings("ignore", message="numpy.ufunc size changed") import numpy as np import matplotlib.pyplot as plt import pandas as pd import seaborn as sns %matplotlib inline import ipywidgets as widgets from ipywidgets import interact, interactive, fixed, interact_manual import nbinteract as nbi sns.set() sns.set_context('talk') np.set_printoptions(threshold=20, precision=2, suppress=True) pd.options.display.max_rows = 7 pd.options.display.max_columns = 8 pd.set_option('precision', 2) # This option stops scientific notation for pandas # pd.set_option('display.float_format', '{:.2f}'.format) ``` ``` # HIDDEN import scipy.stats as stats ``` 幾乎所有現實世界中的現象都包含一定程度的隨機性，使得數據生成和收集本身就是隨機過程。由于我們將模型與這些數據相匹配，因此我們的模型也包含隨機性。為了數學上表示這些隨機過程，我們使用隨機變量。 **隨機變量**是一個代數變量，表示由概率事件確定的**數值。在本書中，我們總是使用大寫字母（不是希臘字母），如$X$或$Y$來表示隨機變量。盡管隨機變量可以代表離散的（如 10 人樣本中男性的數量）或連續的數量（如洛杉磯的平均溫度），但我們將僅在本教材中使用離散隨機變量。** 我們必須總是指定一個給定的隨機變量代表什么。例如，我們可以寫下隨機變量$x$表示 10 個硬幣翻轉中的頭數。隨機變量的定義決定了它可以接受的值。在本例中，$x$只能包含 0$到 10$之間的值。 我們還必須能夠確定隨機變量接受每個可能值的概率。例如，$x=0$被寫為$p（x=0）=（0.5）^ 10$的概率，我們同樣可以計算$x$是任何以$0，1，ldots，10 為單位的值的概率。 ### 概率質量函數 隨機變量$x$的**概率質量函數（pmf）**或**分布**提供$x$接受其每個可能值的概率。如果我們將$\mathbb x 設為$x$可以接受的一組值，并且$x$是$\mathbb x 中的特定值，則$x$的 PMF 必須滿足以下規則： $$ 1) \sum_{x \in \mathbb{X}} P(X = x) = 1 $$$$ 2) \text{ For all } x \in \mathbb{X}, 0 \leq P(X = x) \leq 1 $$ 第一條規則規定，$x$sum 到$1$的所有可能值的概率。 第二條規則規定，給定值$x$的每個概率必須介于$0$和$1$之間。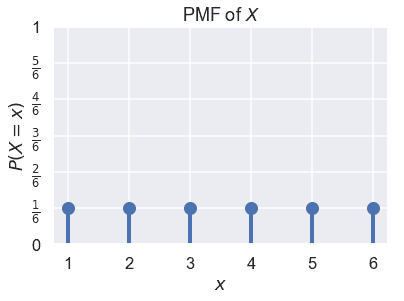 假設我們讓 x 美元代表一個公平的六面骰子的一個骰子的結果。我們知道，$x 在 1、2、3、4、5、6 中，$p（x=1）=p（x=2）=\ldots=p（x=6）=\frac 1 6 美元。我們可以繪制$x$的 PMF 作為概率分布： ``` # HIDDEN def plot_pmf(xs, probs, rv_name='X'): plt.plot(xs, probs, 'ro', ms=12, mec='b', color='b') plt.vlines(xs, 0, probs, colors='b', lw=4) plt.xlabel('$x$') plt.ylabel('$P(X = x)$') plt.ylim(0, 1) plt.title('PMF of $X$'); ``` ``` # HIDDEN xk = np.arange(1, 7) pk = (1/6, 1/6, 1/6, 1/6, 1/6, 1/6) plot_pmf(np.arange(1, 7), np.repeat(1/6, 6)) plt.yticks(np.linspace(0, 1, 7), ('0', r'$\frac{1}{6}$', r'$\frac{2}{6}$', r'$\frac{3}{6}$', r'$\frac{4}{6}$', r'$\frac{5}{6}$', '1')); ```  ### 關節分布 單隨機變量的 PMF 概念自然地擴展到多隨機變量的聯合分布。特別是，兩個或多個隨機變量的**聯合分布**產生這些隨機變量同時接受一組特定值的概率。 例如，讓隨機變量$X$表示 10 個硬幣翻轉中的頭數，讓$Y$表示同一組 10 個硬幣翻轉中的尾部數。我們可以注意到： $$P(X=0, Y=10) = P(X=10, Y=0) = (0.5)^{10}$$ 同時$P（x=6，y=6）=0 美元，因為我們不可能在 10 個硬幣翻轉中有 6 個頭部和 6 個尾部。 #### 邊際分布 有時，我們從兩個隨機變量$X$和$Y$的聯合分布開始，但只想找到$X$的分布。這個分布稱為**邊際分布**。為了找出$x$接受某個特定值的概率，我們必須考慮所有可能的$y$值（用$\mathbb y 表示），這些值可以與$x$同時發生，并對所有這些聯合概率求和： $$ \begin{aligned} \sum_{y \in \mathbb{Y}} P(X=x, Y=y) &= P(X=x) \end{aligned} $$ 我們可以證明如下身份： $$ \begin{aligned} \sum_{y \in \mathbb{Y}} P(X=x, Y=y) &= \sum_{y \in \mathbb{Y}} P(X=x) \times P(Y=y \; \vert \; X=x)\\ &= P(X=x) \times \sum_{y \in \mathbb{Y}} P(Y=y \; \vert \; X=x)\\ &= P(X=x) \times 1 \\ &= P(X=x) \end{aligned} $$ 在這個證明的最后一行中，我們將$y\；\vert\；x=x$作為一個帶有未知 pmf 的隨機變量。這一點很重要，因為我們使用了一個屬性，即 pmf 中的概率總和為 1 美元，這意味著在 mathbb y p（y=y \ vert \ x=x）=1 美元。 #### 獨立隨機變量 像事件一樣，兩個隨機變量可以是相依的或獨立的。任何兩個隨機變量都是獨立的，只要知道一個變量的結果不會改變觀察另一個變量任何結果的概率。 例如，假設我們把一枚硬幣擲十次，讓$x$作為頭的數目，讓$y$作為尾的數目。顯然，$x$和$y$是因變量，因為知道$x=0$意味著$y$必須等于$10$。如果我們沒有觀察到$X$的值，$Y$可以以非零概率在$0$和$10$之間取任何值。 我們可以做兩組十次翻轉。如果$x$是第一組翻轉中的頭數，$y$是第二組翻轉中的頭數，$x$和$y$是獨立的，因為第一組十個翻轉的結果不會影響第二組翻轉的結果。 ### 年齡[?](#An-Example-with-Ages)的例子 假設我們有一個由四個人組成的小數據集： ``` # HIDDEN data={"Name":["Carol","Bob","John","Dave"], 'Age': [50,52,51,50]} people = pd.DataFrame(data) people ``` | | 姓名 | 年齡 | | --- | --- | --- | | 零 | 頌歌 | 五十 | | --- | --- | --- | | 1 個 | 鮑勃 | 五十二 | | --- | --- | --- | | 二 | 約翰 | 五十一 | | --- | --- | --- | | 三 | 戴夫 | 50 | | --- | --- | --- | 假設我們從這個數據集中抽取兩個人進行替換。如果隨機變量$Z$代表樣本中第一和第二個人的年齡差異，那么$Z$的 PMF 是什么？ 為了解決這個問題，我們定義了兩個新的隨機變量。我們將$X$定義為第一個人的年齡，$Y$定義為第二個人的年齡。那么，$Z=X-Y$就可以了。然后，我們找到 x$和 y$的聯合概率分布：x$和 y$可以同時接受的每個值的概率。在這種情況下，請注意$x$和$y$是獨立的，分布相同；這兩個隨機變量表示來自同一數據集的兩個獨立的提取，第一個提取對第二個提取沒有影響。例如，$x=51$和$y=50$的概率是$p（x=51，y=50）=\frac 1 4 \cdot\frac 2 4 frac 2 16。以類似的方式，我們得到： | | Y＝50 美元 | Y＝51 美元 | Y＝52 美元 | | --- | --- | --- | --- | | X＝50 美元 | 4/16 | 2/16 | 2/16 | | X＝51 美元 | 2/16 | 1/16 | 1/16 | | X＝52 美元 | 2/16 | 1/16 | 1/16 | 現在讓我們考慮一下這樣的情況：我們從上面相同的數據集中抽取兩個人，但沒有替換。如前所述，我們將$X$定義為第一個人的年齡，$Y$定義為第二個人的年齡，$Z=X-Y$。但是，現在$X$和$Y$不是獨立的；例如，如果我們知道$X=51$，那么$Y\neq 51$。我們發現 X 美元和 Y 美元的聯合分配如下： | | $Y=50$ | $Y=51$ | $Y=52$ | | --- | --- | --- | --- | | $X=50$ | 2/12 | 2/12 | 2/12 | | $X=51$ | 2/12 | 零 | 1/12 | | $X=52$ | 2/12 | 1/12 | 0 | 我們還可以從表中找到$Y$的邊際分布。 $$ \begin{aligned} P(Y = 50) &= P(Y = 50, X = 50) + P(Y = 50, X = 51) + P(Y = 50, X = 52) \\ &= \frac{2}{12} + \frac{2}{12} + \frac{2}{12} \\ &= \frac{1}{2} \\ P(Y = 51) &= \frac{2}{12} + 0 + \frac{1}{12} = \frac{1}{4} \\ P(Y = 52) &= \frac{2}{12} + \frac{1}{12} + 0 = \frac{1}{4} \end{aligned} $$ 注意，我們對上面的聯合分布表的每一列進行了匯總。我們可以想象計算每一列的總和，并將結果寫在下表的空白處；這是術語邊際分布的起源。 您還應該注意到，$X$和$Y$在沒有替換的情況下采樣時是不獨立的。例如，如果 x=52 美元，$y\neq 52 美元。然而，$x$和$y$的邊際分布仍然相同。 ## 摘要[?](#Summary) 在本節中，我們將介紹隨機變量，即根據隨機過程獲取值的數學變量。這些結果必須完全準確地定義，每個結果都必須有明確的發生概率。隨機變量可以用來表示許多隨機現象，包括數據收集過程。