# 二、數據生成 > 原文：[DS-100/textbook/notebooks/ch02](https://nbviewer.jupyter.org/github/DS-100/textbook/tree/master/notebooks/ch02/) > > 校驗：[飛龍](https://github.com/wizardforcel) > > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 數據科學很難成為沒有數據的科學。 因此重要的是，我們通過了解我們的數據是如何生成的，來啟動任何數據分析。 在本章中，我們將討論數據來源。 雖然術語“數據來源”通常指的是數據的整個歷史，以及它隨時間變化的位置，但我們將在本教科書中使用這個術語，來指代我們的數據的生成過程。 許多人得出了不成熟的結論，因為他們對數據的理解不夠細致; 我們將討論一個例子來證明，概率抽樣在數據科學中的重要性。 ## Dewey 擊敗了 Truman 在 1948 年的美國總統大選中，紐約州州長托馬斯杜威（Thomas Dewey）與現任的杜魯門（Harry Truman）競爭。 像往常一樣，一些投票機構進行民意調查，來預測哪個候選人更有可能贏得選舉。 ### 1936 年：以前的民意調查災難 在 1936 年，1948 年的三次選舉之前，《文學文摘》（Literary Digest）預言，富蘭克林·德拉諾·羅斯福會遇到斷崖式下跌，這使其聲名狼藉。為了做出這個斷言，該雜志根據電話和車管局調查了 200 多萬人的樣本。 你可能知道，這種抽樣方案存在抽樣偏差：那些擁有電話和汽車的人往往比沒有的人更富有。 在這種情況下，抽樣偏差如此之大，足以使《文學文摘》認為羅斯福只有 43% 的大眾選票，而他最終以 61% 的大眾選票勝出，相差近 20%，這是有史以來，由民意調查引發的最大的錯誤。“文學文摘”不久之后就停刊了 [1]。 > [1] <https://www.qualtrics.com/blog/the-1936-election-a-polling-catastrophe/> ### 1948 年：蓋洛普（Gallup）民意調查 為了從過去的錯誤中學習，蓋洛普民意調查采用了一種稱為配額抽樣的方法，來預測 1948 年選舉的結果。 在他們的抽樣方案中，每位采訪者都會調查來自每個特征類別的一定數量的人。 例如，采訪者需要采訪不同年齡，種族和收入水平的男性和女性，來匹配美國人口普查的人口特征。 這確保了民意調查不會遺漏投票人群的重要子分組。 使用這種方法，蓋洛普民意調查預測，托馬斯杜威將比哈里杜魯門多贏得 5% 的大眾選票。 這種差異非常顯著，眾所周知，《芝加哥論壇報》（ Chicago Tribune）的標題是“杜威擊敗杜魯門”：  ### 配額抽樣的問題 雖然配額抽樣確實有助于民意調查者減少抽樣偏差，但它以另一種方式引入了偏差。蓋洛普民意調查機構對其采訪者說，只要他們實現了配額，他們就可以采訪他們想要的任何人。為什么采訪者的投票結果與共和黨人不成比例，以下是一個可能的解釋：當時，共和黨人平均較富裕，而且更有可能居住在較好的社區，這使他們更容易受到采訪。蓋洛普民意調查預測的共和黨票數，將比之前的 3 次選舉的實際結果多出 2 % 至 6%。 這些例子強調了在數據收集過程中，盡可能理解抽樣偏差的重要性。《文學文摘》和蓋洛普民意調查都錯誤地認為，當他們的抽樣方案始終基于人類判斷時，他們的方法是沒有偏差的。 我們現在依靠概率抽樣，一組抽樣方法，為每個樣本的外觀賦予精確的概率，來盡可能減少數據收集過程中的偏差。 ### 大數據？ 在大數據時代，我們試圖通過收集更多數據來應對偏差。 畢竟，我們知道人口普查會向我們提供完美的估計；不管抽樣技術如何，一個非常大的樣本不應該給出幾乎完美的估計值嘛？ 在討論概率抽樣方法來比較兩種方法之后，我們將回到這個問題。 ## 概率抽樣 與任意抽樣不同，概率抽樣允許我們，為抽取特定樣本的事件分配精確的概率。 我們將首先回顧 Data8 中的簡單隨機樣本，然后介紹概率抽樣的兩種替代方法：整群抽樣和分層抽樣。 假設我們有 6 個個體。 我們已經給了每個個體一個 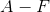 的字母。 ### 簡單隨機抽樣 從這個總體中抽取大小為 2 的簡單隨機樣本，我們可以在單個索引卡片上寫下 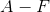 的每個字母，將所有卡片放入一個帽子中，充分混合這些卡片，然后抽出兩張卡片而不看它們。 也就是說，SRS 是無放回隨機抽樣。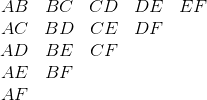 這里是所有可能的大小為 2 的樣本：  我們的大小為 6 的總體，有 15 非可能的樣本，大小 2。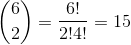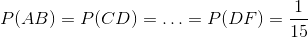 計算可能的樣本數量的另一種方法是：  由于在 SRS 中我們隨機均勻抽樣，這些 15 非樣本中的每個都是等可能選中的：  我們也可以使用這種幾率機制，來回答樣本組成的其他問題。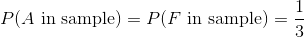 例如：  根據對稱性，我們可以說：  另一種計算 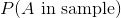 的方法是，確認對于樣本中的 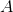，我們需要將其作為第一個彈子或第二個彈子來抽取。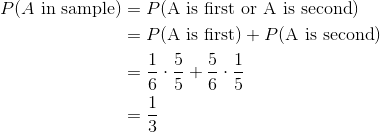  ### 整群抽樣 在整群抽樣中，我們將總體劃分為簇。 然后，我們使用 SRS 來隨機選擇簇而不是個體。 作為一個例子，假設我們從大小為 6 的總體選取個體，我們將他們中的每一個配對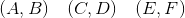：，組成 3 個個體為 2 的簇。 然后，我們使用 SRS 選擇一個簇來產生大小為 2 的樣本。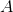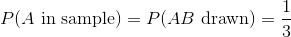 和以前一樣，我們可以計算  在我們樣本中的概率：  與之類似，任何特定個體出現在我們的樣本中的概率是 。 請注意，這與我們的 SRS 相同。 然而，當我們觀察樣本本身時，我們看到了差異。 例如，在 SRS 中獲得 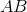 的機會與獲得 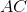 的機會相同，都是 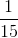。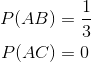 但是，采用這種整群抽樣方案：  由于如果我們只選擇一個簇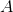， 和 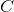 永遠不會出現在同一個樣本中。 整群抽樣仍然是抽率采樣，因為我們可以為每個潛在的抽樣分配一個概率。 然而，所得概率與使用 SRS 不同，取決于總體如何聚集。 為什么使用整群抽樣？ 整群抽樣是最有用的，因為它使得樣本收集更容易。 例如，調查 100 個城鎮的人口比調查遍布整個美國的數千人要容易得多。 這就是今天許多民意調查機構使用整群抽樣形式進行調查的原因。 整群抽樣的主要缺點是，它往往會產生更大的估計差異。 這通常意味著，我們在使用整群抽樣時需要更大的樣本。 請注意，現實比這更復雜，但我們將把細節留給未來的抽樣技術課程。 ### 分層抽樣 在分層抽樣中，我們將總體分成幾層，然后每層產生一個簡單隨機樣本。 在整群抽樣和分層抽樣中，我們將人口分成幾組；在整群抽樣中，我們使用單個 SRS 來選擇組，而在分層抽樣中，我們使用多個 SRS，每組有一個 SRS。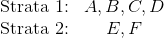 我們可以將我們大小為 6 的總體分成以下幾層：  我們使用 SRS 從每一層中選擇一個個體，來生成一個大小為 2 的樣本。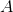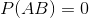這向我們提供了以下可能的樣本：  再次，我們可以計算  在我們樣本中的概率：  但是：  因為 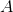 和 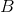 不能出現在同一個樣本中。 與整群抽樣一樣，分層抽樣也是一種概率抽樣方法，它根據總體的分層情況產生不同的概率。 請注意，就像這個例子，層的大小不一定相同。 例如，我們可以根據職業對美國進行分層，然后根據美國職業分布，從每個層級抽取樣本 - 如果美國只有 0.01% 的人是統計人員，我們可以確保我們樣本的 0.01% 將由統計人員組成。 簡單的隨機樣本可能完全忽略了可憐的統計人員！ 你可能已經想到，分層抽樣可能被稱為配額抽樣的合理方式。 它允許研究人員確保總體中的子組，在樣本中得到很好的代表，而不用人為判斷來選擇樣本中的個體。 這通常會使估計差異較小。 然而，分層抽樣有時更難完成，因為我們有時不知道每一層有多大。 在前面的例子中，我們有美國人口普查的優勢，但有些時候我們并不那么幸運。 ### 為什么是概率抽樣？ 我們在 Data8 中看到，概率抽樣使我們能夠量化，我們對估計或預測的不確定性。 只有通過這個精確度，我們才能進行推斷和假設檢驗。 當任何人向你給出 p 值或置信度，而沒有正確解釋他們的抽樣技術時，要小心。 現在我們理解了概率抽樣，讓我們看看卑微的 SRS 與“大數據”相比如何。 ## SRS vs “大數據” 我們之前提到，通過使用大量數據來消除我們冗長的偏差問題，是很有吸引人的。按照定義，人口普查確實會產生無偏估計。如果我們收集大量數據，也許我們不必擔心偏差。 假設我們是 2012 年的民意調查者，試圖預測美國總統選舉的大眾投票，巴拉克·奧巴馬與米特??·羅姆尼競爭。由于我們知道準確的大眾投票結果，因此我們可以比較 SRS 的預測，與大型非隨機數據集（通常稱為行政數據集）的預測，因為它們通常作為某些行政工作的一部分而收集。 我們將比較大小為 400 的 SRS 和大小為 60,000,000 的非隨機樣本。我們的非隨機樣本比我們的 SRS 大近 15 萬倍！由于 2012 年大約有 1.2 億選民，我們可以將我們的非隨機樣本看作一個調查，其中美國所有選民的一半做出了回應（沒有超過 10,000,000 個選民的實際調查）。 ```py # HIDDEN total = 129085410 obama_true_count = 65915795 romney_true_count = 60933504 obama_true = obama_true_count / total romney_true = romney_true_count / total # 1 percent off obama_big = obama_true - 0.01 romney_big = romney_true + 0.01 ``` 這是一個繪圖，比較了非隨機樣本的比例與真實比例。 標有真實值的條形顯示了，每位候選人收到的選票的真實比例。 標有“大”的條形顯示了，我們 6000 萬選民的數據集中的比例。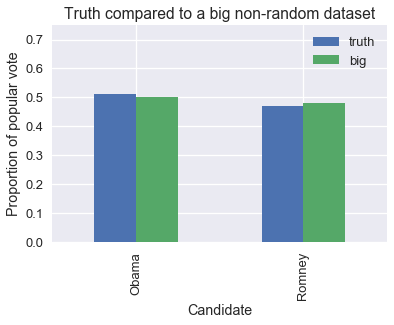 ```py pd.DataFrame({ 'truth': [obama_true, romney_true], 'big': [obama_big, romney_big], }, index=['Obama', 'Romney'], columns=['truth', 'big']).plot.bar() plt.title('Truth compared to a big non-random dataset') plt.xlabel('Candidate') plt.ylabel('Proportion of popular vote') plt.ylim(0, 0.75) None ```  我們可以看到，就像 1948 年的蓋洛普民意調查一樣，我們的大數據集僅僅有點偏向共和黨候選人羅姆尼。盡管如此，這個數據集可以向我們提供準確的預測。 為了檢查，我們可以從總體中模擬抽取大小為 400 的隨機樣本，和大小為 60,000,000 的大型非隨機樣本。 我們將計算每個樣本中的奧巴馬的選票比例，并繪制比例分布圖。 ```py srs_size = 400 big_size = 60000000 replications = 10000 def resample(size, prop, replications): return np.random.binomial(n=size, p=prop, size=replications) / size srs_simulations = resample(srs_size, obama_true, replications) big_simulations = resample(big_size, obama_big, replications) ``` 現在，我們將繪制模擬結果并放上一條紅線，表示投票給奧巴馬的選民的真實比例。 ```py bins = bins=np.arange(0.47, 0.55, 0.005) plt.hist(srs_simulations, bins=bins, alpha=0.7, normed=True, label='srs') plt.hist(big_simulations, bins=bins, alpha=0.7, normed=True, label='big') plt.title('Proportion of Obama Voters for SRS and Big Data') plt.xlabel('Proportion') plt.ylabel('Percent per unit') plt.xlim(0.47, 0.55) plt.ylim(0, 50) plt.axvline(x=obama_true, color='r', label='truth') plt.legend() None ```  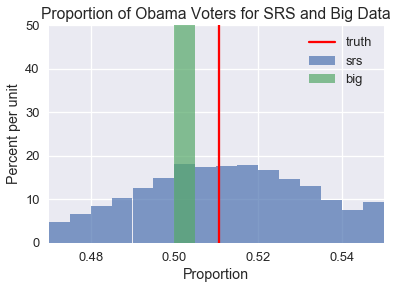正如你所看到的，SRS 分布是分散的，但圍繞著奧巴馬選民的真實總體比例。 另一方面，大型非隨機樣本創建的分布非常狹窄，但沒有一個模擬樣本能夠產生真實總體比例。 如果我們嘗試使用非隨機樣本創建置信區間，則它們都不會包含真實總體比例。 更糟糕的是，由于樣本非常大，置信區間將非常狹窄。我們最終會確信錯誤估計。 事實上，當我們的抽樣方法有偏差時，由于我們收集了更多的數據，我們的估計會變得更糟，因為我們會更加確信不正確的結果，只有當我們的數據集幾乎是人口普查時才會變得更加準確。 數據的質量比它的大小重要得多。 ### 重要結論 在接受數據分析結果之前，仔細檢查數據的質量是值得的。 特別是，我們必須提出以下問題： 數據是否為人口普查（是否包括整個人群）？ 如果是這樣，我們可以直接計算總體的屬性而不必使用推斷。 如果數據是樣本，那么樣本是如何收集的？ 為了正確進行推斷，樣本應該根據概率抽樣方法收集。 在產生結果之前對數據進行了哪些更改？ 這些變化是否會影響數據的質量？ 對于隨機和非隨機大樣本之間的比較的更多細節，我們建議觀看[統計學家 Xiao-Li Meng 的這個講座](https://www.youtube.com/watch?v=yz3jOIHLYhU)。