# 實現損失函數 損失函數對于機器學習算法非常重要。它們測量模型輸出與目標（真值）值之間的距離。在這個秘籍中，我們在 TensorFlow 中展示了各種損失函數實現。 ## 做好準備 為了優化我們的機器學習算法，我們需要評估結果。評估 TensorFlow 中的結果取決于指定損失函數。損失函數告訴 TensorFlow 預測與期望結果相比有多好或多壞。在大多數情況下，我們將有一組數據和一個目標來訓練我們的算法。損失函數將目標與預測進行比較，并給出兩者之間的數值距離。 對于這個秘籍，我們將介紹我們可以在 TensorFlow 中實現的主要損失函數。 要了解不同損失函數的運行方式，我們將在此秘籍中繪制它們。我們將首先啟動一個計算圖并加載`matplotlib`，一個 Python 繪圖庫，如下所示： ```py import matplotlib.pyplot as plt import tensorflow as tf ``` ## 操作步驟 1. 首先，我們將討論回歸的損失函數，這意味著預測連續的因變量。首先，我們將創建一個預測序列和一個作為張量的目標。我們將在-1 和 1 之間輸出 500 x 值的結果。有關輸出的繪圖，請參閱“工作原理...”部分。使用以下代碼： ```py x_vals = tf.linspace(-1., 1., 500) target = tf.constant(0.) ``` 1. L2 范數損失也稱為歐幾里德損失函數。它只是到目標的距離的平方。在這里，我們將計算損失函數，就像目標為零一樣。 L2 范數是一個很大的損失函數，因為它在目標附近非常彎曲，并且算法可以使用這個事實來越慢地收斂到目標，越接近零。我們可以按如下方式實現： ```py l2_y_vals = tf.square(target - x_vals) l2_y_out = sess.run(l2_y_vals) ``` > TensorFlow 具有 L2 范數的內置形式，稱為`nn.l2_loss()`。這個函數實際上是 L2 規范的一半。換句話說，它與前一個相同，但除以 2。 1. L1 范數損失也稱為絕對損失函數。我們不是平衡差異，而是取絕對值。 L1 范數對于異常值比 L2 范數更好，因為對于較大的值，它不是那么陡峭。需要注意的一個問題是 L1 范數在目標處不平滑，這可能導致算法收斂不好。它看起來如下： ```py l1_y_vals = tf.abs(target - x_vals) l1_y_out = sess.run(l1_y_vals) ``` 1. 偽 Huber 損失是 Huber 損失函數的連續且平滑的近似。這種損失函數試圖通過在目標附近凸起并且對于極值不太陡峭來充分利用 L1 和 L2 范數。表格取決于額外的參數 delta，它決定了它的陡峭程度。我們將繪制兩種形式，`delta1 = 0.25`和`delta2 = 5`，以顯示差異，如下所示： ```py delta1 = tf.constant(0.25) phuber1_y_vals = tf.multiply(tf.square(delta1), tf.sqrt(1\. + tf.square((target - x_vals)/delta1)) - 1.) phuber1_y_out = sess.run(phuber1_y_vals) delta2 = tf.constant(5.) phuber2_y_vals = tf.multiply(tf.square(delta2), tf.sqrt(1\. + tf.square((target - x_vals)/delta2)) - 1.) phuber2_y_out = sess.run(phuber2_y_vals) ``` 現在，我們繼續討論分類問題的損失函數。分類損失函數用于在預測分類結果時評估損失。通常，我們的類別類型的輸出是 0 到 1 之間的實數值。然后，我們選擇截止值（通常選擇 0.5）并且如果數字高于截止值，則將結果分類為該類別。在這里，我們考慮分類輸出的各種損失函數： 1. 首先，我們需要重新定義我們的預測（`x_vals`）和`target`。我們將保存輸出并在下一節中繪制它們。使用以下內容： ```py x_vals = tf.linspace(-3., 5., 500) target = tf.constant(1.) targets = tf.fill([500,], 1.) ``` 1. 鉸鏈損失主要用于支持向量機，但也可用于神經網絡。它旨在計算兩個目標類 1 和-1 之間的損失。在下面的代碼中，我們使用目標值`1`，因此我們的預測越接近 1，損失值越低： ```py hinge_y_vals = tf.maximum(0., 1\. - tf.multiply(target, x_vals)) hinge_y_out = sess.run(hinge_y_vals) ``` 1. 二元情形的交叉熵損失有時也稱為邏輯損失函數。它是在我們預測兩個 0 或 1 類時出現的。我們希望測量從實際類（0 或 1）到預測值的距離，預測值通常是介于 0 和 1 之間的實數。為了測量這個距離，我們可以使用信息論中的交叉熵公式，如下： ```py xentropy_y_vals = - tf.multiply(target, tf.log(x_vals)) - tf.multiply((1\. - target), tf.log(1\. - x_vals)) xentropy_y_out = sess.run(xentropy_y_vals) ``` 1. Sigmoid 交叉熵損失與之前的損失函數非常相似，除了我們在將它們置于交叉熵損失之前使用 sigmoid 函數轉換 x 值，如下所示： ```py xentropy_sigmoid_y_vals = tf.nn.sigmoid_cross_entropy_with_logits_v2(logits=x_vals, labels=targets) xentropy_sigmoid_y_out = sess.run(xentropy_sigmoid_y_vals) ``` 1. 加權交叉熵損失是 S 形交叉熵損失的加權版本。我們對積極目標給予了重視。舉個例子，我們將正面目標加權 0.5，如下： ```py weight = tf.constant(0.5) xentropy_weighted_y_vals = tf.nn.weighted_cross_entropy_with_logits(logits=x_vals, targets=targets, pos_weight=weight) xentropy_weighted_y_out = sess.run(xentropy_weighted_y_vals) ``` 1. Softmax 交叉熵損失在非標準化輸出上運行。當只有一個目標類別而不是多個目標類別時，此函數用于測量損失。因此，函數通過 softmax 函數將輸出轉換為概率分布，然后根據真實概率分布計算損失函數，如下所示： ```py unscaled_logits = tf.constant([[1., -3., 10.]]) target_dist = tf.constant([[0.1, 0.02, 0.88]]) softmax_xentropy = tf.nn.softmax_cross_entropy_with_logits_v2(logits=unscaled_logits, labels=target_dist) print(sess.run(softmax_xentropy)) [ 1.16012561] ``` 1. 稀疏 softmax 交叉熵損失與前一個相同，除了目標是概率分布，它是哪個類別為真的索引。我們只傳遞真值的類別的索引，而不是稀疏的全零目標向量，其值為 1，如下所示： ```py unscaled_logits = tf.constant([[1., -3., 10.]]) sparse_target_dist = tf.constant([2]) sparse_xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=unscaled_logits, labels=sparse_target_dist) print(sess.run(sparse_xentropy)) [ 0.00012564] ``` ## 工作原理 以下是如何使用`matplotlib`繪制回歸損失函數： ```py x_array = sess.run(x_vals) plt.plot(x_array, l2_y_out, 'b-', label='L2 Loss') plt.plot(x_array, l1_y_out, 'r--', label='L1 Loss') plt.plot(x_array, phuber1_y_out, 'k-.', label='P-Huber Loss (0.25)') plt.plot(x_array, phuber2_y_out, 'g:', label='P-Huber Loss (5.0)') plt.ylim(-0.2, 0.4) plt.legend(loc='lower right', prop={'size': 11}) plt.show() ``` 我們得到以下圖作為上述代碼的輸出：  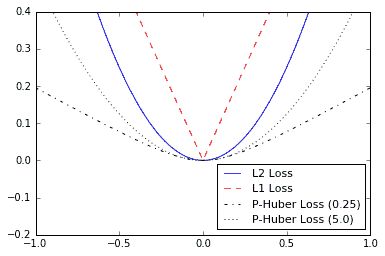圖 4：繪制各種回歸損失函數 以下是如何使用`matplotlib`繪制各種分類損失函數： ```py x_array = sess.run(x_vals) plt.plot(x_array, hinge_y_out, 'b-''', label='Hinge Loss''') plt.plot(x_array, xentropy_y_out, 'r--''', label='Cross' Entropy Loss') plt.plot(x_array, xentropy_sigmoid_y_out, 'k-.''', label='Cross' Entropy Sigmoid Loss') plt.plot(x_array, xentropy_weighted_y_out, g:''', label='Weighted' Cross Enropy Loss (x0.5)') plt.ylim(-1.5, 3) plt.legend(loc='lower right''', prop={'size''': 11}) plt.show() ``` 我們從前面的代碼中得到以下圖： 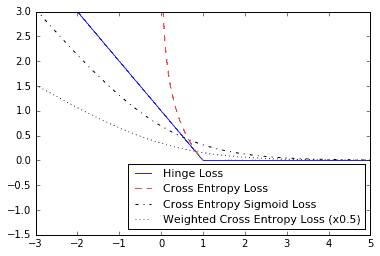Figure 5: Plots of classification loss functions ## 更多 這是一個總結我們描述的不同損失函數的表： | 損失函數 | 任務 | 優點 | 缺點 | | --- | --- | --- | --- | | L2 | 回歸 | 更穩定 | 不太健壯 | | L1 | 回歸 | 更強大 | 不太穩定 | | 偽胡伯 | 回歸 | 更穩健，更穩定 | 還有一個參數 | | 合頁 | 分類 | 創建 SVM 中使用的最大邊距 | 受到異常值影響的無限損失 | | 交叉熵 | 分類 | 更穩定 | 無限損失，不那么強大 | 剩余的分類損失函數都與交叉熵損失的類型有關。交叉熵 sigmoid los 函數用于未縮放的 logits，并且優于計算 sigmoid 然后交叉熵，因為 TensorFlow 具有更好的內置方式來處理數字邊緣情況。 softmax 交叉熵和稀疏 softmax 交叉熵也是如此。 > 這里描述的大多數分類損失函數用于兩類預測。通過對每個預測/目標上的交叉熵項求和，可以將其擴展到多個類。 評估模型時還需要考慮許多其他指標。以下列出了一些需要考慮的事項： | 模型指標 | 描述 | | --- | --- | | R 平方（確定系數） | 對于線性模型，這是因變量的方差比例，由獨立數據解釋。對于具有大量特征的模型，請考慮使用調整后的 R 平方。 | | 均方根誤差 | 對于連續模型，它通過平均平方誤差的平方根來測量預測與實際之間的差異。 | | 混淆矩陣 | 對于分類模型，我們查看預測類別與實際類別的矩陣。一個完美的模型具有沿對角線的所有計數。 | | 召回 | 對于分類模型，這是所有預測陽性的真陽性分數。 | | 精確 | 對于分類模型，這是所有實際正數的真實積極分數。 | | F-得分 | 對于分類模型，這是精度和召回的調和平均值。 |