# 使用多層神經網絡 我們現在將通過在低出生體重數據集上使用多層神經網絡將我們對不同層的知識應用于實際數據。 ## 做好準備 現在我們知道如何創建神經網絡并使用層，我們將應用此方法，以預測低出生體重數據集中的出生體重。我們將創建一個具有三個隱藏層的神經網絡。低出生體重數據集包括實際出生體重和出生體重是否高于或低于 2,500 克的指標變量。在這個例子中，我們將目標設為實際出生體重（回歸），然后在最后查看分類的準確率。最后，我們的模型應該能夠確定出生體重是否為&lt; 2,500 克。 ## 操作步驟 我們按如下方式處理秘籍： 1. 我們將首先加載庫并初始化我們的計算圖，如下所示： ```py import tensorflow as tf import matplotlib.pyplot as plt import os import csv import requests import numpy as np sess = tf.Session() ``` 1. 我們現在將使用`requests`模塊從網站加載數據。在此之后，我們將數據拆分為感興趣的特征和目標值，如下所示： ```py # Name of data file birth_weight_file = 'birth_weight.csv' birthdata_url = 'https://github.com/nfmcclure/tensorflow_cookbook/raw/master' \ '/01_Introduction/07_Working_with_Data_Sources/birthweight_data/birthweight.dat' # Download data and create data file if file does not exist in current directory if not os.path.exists(birth_weight_file): birth_file = requests.get(birthdata_url) birth_data = birth_file.text.split('\r\n') birth_header = birth_data[0].split('\t') birth_data = [[float(x) for x in y.split('\t') if len(x) >= 1] for y in birth_data[1:] if len(y) >= 1] with open(birth_weight_file, "w") as f: writer = csv.writer(f) writer.writerows([birth_header]) writer.writerows(birth_data) # Read birth weight data into memory birth_data = [] with open(birth_weight_file, newline='') as csvfile: csv_reader = csv.reader(csvfile) birth_header = next(csv_reader) for row in csv_reader: birth_data.append(row) birth_data = [[float(x) for x in row] for row in birth_data] # Pull out target variable y_vals = np.array([x[0] for x in birth_data]) # Pull out predictor variables (not id, not target, and not birthweight) x_vals = np.array([x[1:8] for x in birth_data]) ``` 1. 為了幫助實現可重復性，我們現在需要為 NumPy 和 TensorFlow 設置隨機種子。然后我們聲明我們的批量大小如下： ```py seed = 4 tf.set_random_seed(seed) np.random.seed(seed) batch_size = 100 ``` 1. 接下來，我們將數據分成 80-20 訓練測試分組。在此之后，我們需要正則化我們的輸入特征，使它們在 0 到 1 之間，具有最小 - 最大縮放比例，如下所示： ```py train_indices = np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False) test_indices = np.array(list(set(range(len(x_vals))) - set(train_indices))) x_vals_train = x_vals[train_indices] x_vals_test = x_vals[test_indices] y_vals_train = y_vals[train_indices] y_vals_test = y_vals[test_indices] # Normalize by column (min-max norm) def normalize_cols(m, col_min=np.array([None]), col_max=np.array([None])): if not col_min[0]: col_min = m.min(axis=0) if not col_max[0]: col_max = m.max(axis=0) return (m-col_min) / (col_max - col_min), col_min, col_max x_vals_train, train_min, train_max = np.nan_to_num(normalize_cols(x_vals_train)) x_vals_test, _, _ = np.nan_to_num(normalize_cols(x_vals_test), train_min, train_max) ``` > 歸一化輸入特征是一種常見的特征轉換，尤其適用于神經網絡。如果我們的數據以 0 到 1 的中心為激活函數，它將有助于收斂。 1. 由于我們有多個層具有相似的初始化變量，我們現在需要創建一個函數來初始化權重和偏差。我們使用以下代碼執行此操作： ```py def init_weight(shape, st_dev): weight = tf.Variable(tf.random_normal(shape, stddev=st_dev)) return weight def init_bias(shape, st_dev): bias = tf.Variable(tf.random_normal(shape, stddev=st_dev)) return bias ``` 1. 我們現在需要初始化占位符。將有八個輸入特征和一個輸出，出生權重以克為單位，如下所示： ```py x_data = tf.placeholder(shape=[None, 8], dtype=tf.float32) y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32) ``` 1. 對于所有三個隱藏層，完全連接的層將使用三次。為了防止重復代碼，我們將在初始化模型時創建一個層函數，如下所示： ```py def fully_connected(input_layer, weights, biases): layer = tf.add(tf.matmul(input_layer, weights), biases) return tf.nn.relu(layer) ``` 1. 現在是時候創建我們的模型了。對于每個層（和輸出層），我們將初始化權重矩陣，偏置矩陣和完全連接的層。對于此示例，我們將使用大小為 25,10 和 3 的隱藏層： > 我們使用的模型將有 522 個變量適合。為了得到這個數字，我們可以看到數據和第一個隱藏層之間有`8*25 +25=225`變量。如果我們以這種方式繼續添加它們，我們將有`225+260+33+4=522`變量。這遠遠大于我們在邏輯回歸模型中使用的九個變量。 ```py # Create second layer (25 hidden nodes) weight_1 = init_weight(shape=[8, 25], st_dev=10.0) bias_1 = init_bias(shape=[25], st_dev=10.0) layer_1 = fully_connected(x_data, weight_1, bias_1) # Create second layer (10 hidden nodes) weight_2 = init_weight(shape=[25, 10], st_dev=10.0) bias_2 = init_bias(shape=[10], st_dev=10.0) layer_2 = fully_connected(layer_1, weight_2, bias_2) # Create third layer (3 hidden nodes) weight_3 = init_weight(shape=[10, 3], st_dev=10.0) bias_3 = init_bias(shape=[3], st_dev=10.0) layer_3 = fully_connected(layer_2, weight_3, bias_3) # Create output layer (1 output value) weight_4 = init_weight(shape=[3, 1], st_dev=10.0) bias_4 = init_bias(shape=[1], st_dev=10.0) final_output = fully_connected(layer_3, weight_4, bias_4) ``` 1. 我們現在將使用 L1 損失函數（絕對值），聲明我們的優化器（使用 Adam 優化），并按如下方式初始化變量： ```py loss = tf.reduce_mean(tf.abs(y_target - final_output)) my_opt = tf.train.AdamOptimizer(0.05) train_step = my_opt.minimize(loss) init = tf.global_variables_initializer() sess.run(init) ``` > 雖然我們在前一步驟中用于 Adam 優化函數的學習率是 0.05，但有研究表明較低的學習率始終產生更好的結果。對于這個秘籍，由于數據的一致性和快速收斂的需要，我們使用了更大的學習率。 1. 接下來，我們需要訓練我們的模型進行 200 次迭代。我們還將包含存儲`train`和`test`損失的代碼，選擇隨機批量大小，并每 25 代打印一次狀態，如下所示： ```py # Initialize the loss vectors loss_vec = [] test_loss = [] for i in range(200): # Choose random indices for batch selection rand_index = np.random.choice(len(x_vals_train), size=batch_size) # Get random batch rand_x = x_vals_train[rand_index] rand_y = np.transpose([y_vals_train[rand_index]]) # Run the training step sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y}) # Get and store the train loss temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y}) loss_vec.append(temp_loss) # Get and store the test loss test_temp_loss = sess.run(loss, feed_dict={x_data: x_vals_test, y_target: np.transpose([y_vals_test])}) test_loss.append(test_temp_loss) if (i+1)%25==0: print('Generation: ' + str(i+1) + '. Loss = ' + str(temp_loss)) ``` 1. 上一步應該產生以下輸出： ```py Generation: 25\. Loss = 5922.52 Generation: 50\. Loss = 2861.66 Generation: 75\. Loss = 2342.01 Generation: 100\. Loss = 1880.59 Generation: 125\. Loss = 1394.39 Generation: 150\. Loss = 1062.43 Generation: 175\. Loss = 834.641 Generation: 200\. Loss = 848.54 ``` 1. 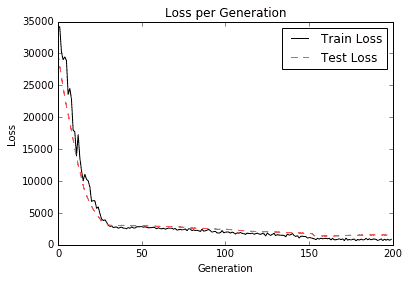以下是使用`matplotlib`繪制訓練和測試損失的代碼片段： ```py plt.plot(loss_vec, 'k-', label='Train Loss') plt.plot(test_loss, 'r--', label='Test Loss') plt.title('Loss per Generation') plt.xlabel('Generation') plt.ylabel('Loss') plt.legend(loc='upper right') plt.show() ``` 我們通過繪制下圖來繼續秘籍：  圖 6：在上圖中，我們繪制了我們訓練的神經網絡的訓練和測試損失，以克數表示出生體重。請注意，大約 30 代后我們已經達到了良好的模型 1. 我們現在想將我們的出生體重結果與我們之前的后勤結果進行比較。使用邏輯線性回歸（如[第 3 章](../Text/20.html)中的實現邏輯回歸秘籍，線性回歸），我們在數千次迭代后獲得了大約 60％的準確率結果。為了將其與我們在上一節中所做的進行比較，我們需要輸出訓練并測試回歸結果，并通過創建指標（如果它們高于或低于 2,500 克）將其轉換為分類結果。要找出模型的準確率，我們需要使用以下代碼： ```py actuals = np.array([x[1] for x in birth_data]) test_actuals = actuals[test_indices] train_actuals = actuals[train_indices] test_preds = [x[0] for x in sess.run(final_output, feed_dict={x_data: x_vals_test})] train_preds = [x[0] for x in sess.run(final_output, feed_dict={x_data: x_vals_train})] test_preds = np.array([1.0 if x<2500.0 else 0.0 for x in test_preds]) train_preds = np.array([1.0 if x<2500.0 else 0.0 for x in train_preds]) # Print out accuracies test_acc = np.mean([x==y for x,y in zip(test_preds, test_actuals)]) train_acc = np.mean([x==y for x,y in zip(train_preds, train_actuals)]) print('On predicting the category of low birthweight from regression output (<2500g):') print('Test Accuracy: {}'.format(test_acc)) print('Train Accuracy: {}'.format(train_acc)) ``` 1. 上一步應該產生以下輸出： ```py Test Accuracy: 0.631578947368421 Train Accuracy: 0.7019867549668874 ``` ## 工作原理 在這個秘籍中，我們創建了一個回歸神經網絡，其中包含三個完全連接的隱藏層，以預測低出生體重數據集的出生體重。當將其與物流輸出進行比較以預測高于或低于 2,500 克時，我們獲得了類似的結果并且在更少的幾代中實現了它們。在下一個方案中，我們將嘗試通過使其成為多層邏輯類神經網絡來改進邏輯回歸。