# 理解線性回歸中的損失函數 了解損失函數在算法收斂中的作用非常重要。在這里，我們將說明 L1 和 L2 損失函數如何影響線性回歸中的收斂。 ## 做好準備 我們將使用與先前秘籍中相同的虹膜數據集，但我們將更改損失函數和學習率以查看收斂如何變化。 ## 操作步驟 我們按如下方式處理秘籍： 1. 程序的開始與上一個秘籍相同，直到我們達到我們的損失函數。我們加載必要的庫，啟動會話，加載數據，創建占位符，并定義我們的變量和模型。需要注意的一點是，我們正在提取學習率和模型迭代。我們這樣做是因為我們希望顯示快速更改這些參數的效果。使用以下代碼： ```py import matplotlib.pyplot as plt import numpy as np import tensorflow as tf from sklearn import datasets sess = tf.Session() iris = datasets.load_iris() x_vals = np.array([x[3] for x in iris.data]) y_vals = np.array([y[0] for y in iris.data]) batch_size = 25 learning_rate = 0.1 # Will not converge with learning rate at 0.4 iterations = 50 x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32) y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32) A = tf.Variable(tf.random_normal(shape=[1,1])) b = tf.Variable(tf.random_normal(shape=[1,1])) model_output = tf.add(tf.matmul(x_data, A), b) ``` 1. 我們的損失函數將變為 L1 損失（`loss_l1`），如下所示： ```py loss_l1 = tf.reduce_mean(tf.abs(y_target - model_output)) ``` 1. 現在，我們通過初始化變量，聲明我們的優化器以及通過訓練循環迭代數據來恢復。請注意，我們也在節省每一代的損失來衡量收斂。使用以下代碼： ```py init = tf.global_variables_initializer() sess.run(init) my_opt_l1 = tf.train.GradientDescentOptimizer(learning_rate) train_step_l1 = my_opt_l1.minimize(loss_l1) loss_vec_l1 = [] for i in range(iterations): rand_index = np.random.choice(len(x_vals), size=batch_size) rand_x = np.transpose([x_vals[rand_index]]) rand_y = np.transpose([y_vals[rand_index]]) sess.run(train_step_l1, feed_dict={x_data: rand_x, y_target: rand_y}) temp_loss_l1 = sess.run(loss_l1, feed_dict={x_data: rand_x, y_target: rand_y}) loss_vec_l1.append(temp_loss_l1) if (i+1)%25==0: print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b))) plt.plot(loss_vec_l1, 'k-', label='L1 Loss') plt.plot(loss_vec_l2, 'r--', label='L2 Loss') plt.title('L1 and L2 Loss per Generation') plt.xlabel('Generation') plt.ylabel('L1 Loss') plt.legend(loc='upper right') plt.show() ``` ## 工作原理 在選擇損失函數時，我們還必須選擇適合我們問題的相應學習率。在這里，我們將說明兩種情況，一種是首選 L2，另一種是首選 L1。 如果我們的學習率很小，我們的收斂會花費更多時間。但是如果我們的學習速度太大，我們的算法就會遇到問題從不收斂。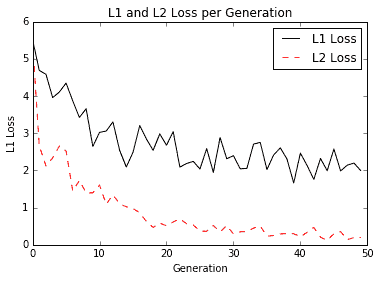下面是當學習率為 0.05 時，虹膜線性回歸問題的 L1 和 L2 損失的損失函數圖：  圖 5：虹膜線性回歸問題的學習率為 0.05 的 L1 和 L2 損失 學習率為 0.05 時，似乎 L2 損失是首選，因為它會收斂到較低的損失。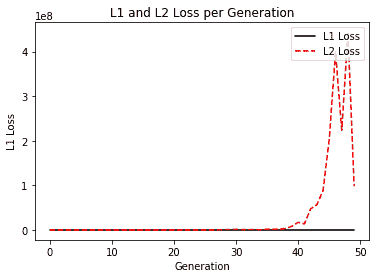下面是我們將學習率提高到 0.4 時的損失函數圖：  圖 6：虹膜線性回歸問題的 L1 和 L2 損失，學習率為 0.4;請注意，由于 y 軸的高比例，L1 損失不可見 在這里，我們可以看到高學習率可以在 L2 范數中超調，而 L1 范數收斂。 ## 更多 為了理解正在發生的事情，我們應該看看大學習率和小學習率如何影響 L1 規范和 L2 規范。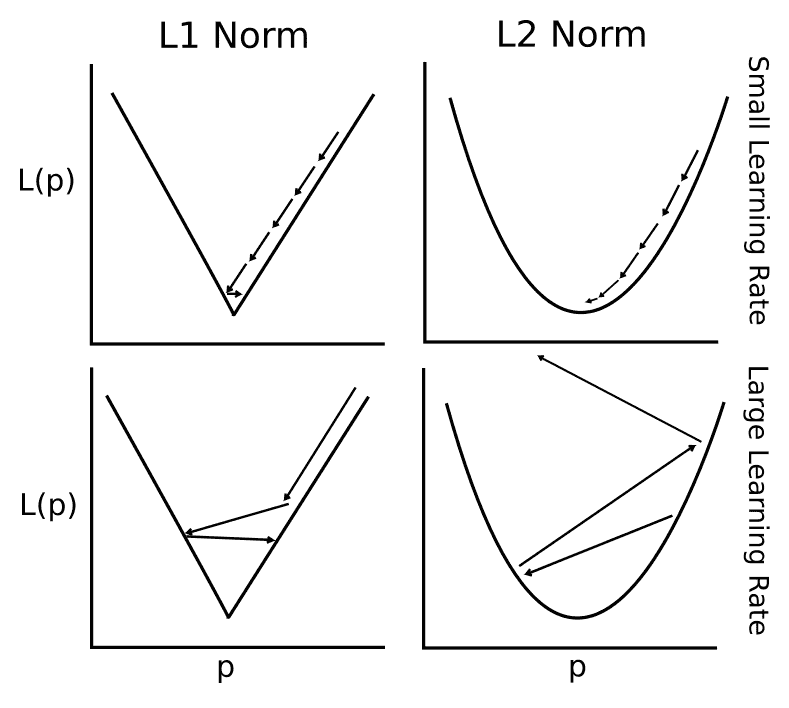為了使這個可視化，我們查看兩個規范的學習步驟的一維表示，如下所示：  圖 7：學習率越來越高的 L1 和 L2 規范會發生什么