# 使用遺傳算法 TensorFlow 還可用于更新我們可以在計算圖中表達的任何迭代算法。一種這樣的迭代算法是遺傳算法，即優化過程。 ## 做好準備 在本文中，我們將說明如何實現簡單的遺傳算法。遺傳算法是優化任何參數空間（離散，連續，平滑，非平滑等）的一種方法。我們的想法是創建一組隨機初始化的解決方案，并應用選擇，重組和變異來生成新的（可能更好的）子解決方案。整個想法取決于我們可以通過查看個人解決問題的程度來計算個體解決方案的適用性。 通常，遺傳算法的概要是從隨機初始化的群體開始，根據它們的適應性對它們進行排序，然后選擇最適合的個體來隨機重組（或交叉）以創建新的子解決方案。然后，這些子解決方案會稍微突變，以產生新的和看不見的改進，然后再添加回父群體。在我們將孩子和父母結合起來之后，我們再次重復整個過程。 停止遺傳算法的標準各不相同，但出于我們的目的，我們將迭代它們一定數量的世代。當我們最適合的人達到理想的適應水平或者在這么多代之后最大適應度沒有改變時，我們也可以停止。 對于這個秘籍，我們將簡單地說明如何在 Tensorflow 中執行此操作。我們要解決的問題是生成一個最接近地面實況函數的個體（50 個浮點數的數組）`f(x) = sin(2πx / 50)`。適應度將是個體與地面事實之間的均方誤差（越高越好）的負值。 ## 操作步驟 1. 我們首先加載腳本所需的庫： ```py import os import numpy as np import matplotlib.pyplot as plt import tensorflow as tf ``` 1. 接下來，我們將設置遺傳算法的參數。在這里，我們將有`100`個體，每個個體的長度為`50`。選擇百分比為 20％（保持前 20 名個人）。突變將被設置為特征數量的倒數，這是突變開始的常見位置。這意味著我們希望每個子解決方案的一個特征發生變化。我們將為`200`世代運行遺傳算法： ```py pop_size = 100 features = 50 selection = 0.2 mutation = 1./ features generations = 200 num_parents = int(pop_size*selection) num_children = pop_size - num_parents ``` 1. 我們將初始化圖會話并創建基礎事實函數，我們將使用它來快速計算適應度： ```py sess = tf.Session() # Create ground truth truth = np.sin(2*np.pi*(np.arange(features, dtype=np.float32))/features) ``` 1. 接下來，我們將`population`初始化為具有隨機正常輸入的 TensorFlow 變量： ```py population = tf.Variable(np.random.randn(pop_size, features), dtype=tf.float32) ``` 1. 我們現在可以為遺傳算法創建占位符。占位符是為了事實，也是為了每一代都會改變的數據。由于我們希望父母之間的交叉位置發生變化，并且變異概率/值會發生變化，因此這些將是我們模型中的占位符： ```py truth_ph = tf.placeholder(tf.float32, [1, features]) crossover_mat_ph = tf.placeholder(tf.float32, [num_children, features]) mutation_val_ph = tf.placeholder(tf.float32, [num_children, features]) ``` 1. 現在，我們將計算人口`fitness`（負均方誤差），并找到表現最佳的人： ```py fitness = -tf.reduce_mean(tf.square(tf.subtract(population, truth_ph)), 1) top_vals, top_ind = tf.nn.top_k(fitness, k=pop_size) ``` 1. 為了達到結果和繪圖目的，我們還希望檢索人群中最適合的個體： ```py best_val = tf.reduce_min(top_vals) best_ind = tf.argmin(top_vals, 0) best_individual = tf.gather(population, best_ind) ``` 1. 接下來，我們對父母群體進行排序，并切斷表現最佳的個體，使其成為下一代的父母： ```py population_sorted = tf.gather(population, top_ind) parents = tf.slice(population_sorted, [0, 0], [num_parents, features]) ``` 1. 現在，我們將通過創建隨機洗牌的兩個父矩陣來創建子項。然后，我們將父矩陣乘以 1 和 0 的交叉矩陣，我們將為占位符生成每一代： ```py # Indices to shuffle-gather parents rand_parent1_ix = np.random.choice(num_parents, num_children) rand_parent2_ix = np.random.choice(num_parents, num_children) # Gather parents by shuffled indices, expand back out to pop_size too rand_parent1 = tf.gather(parents, rand_parent1_ix) rand_parent2 = tf.gather(parents, rand_parent2_ix) rand_parent1_sel = tf.multiply(rand_parent1, crossover_mat_ph) rand_parent2_sel = tf.multiply(rand_parent2, tf.subtract(1., crossover_mat_ph)) children_after_sel = tf.add(rand_parent1_sel, rand_parent2_sel) ``` 1. 最后的步驟是改變子項，我們將通過向子矩陣中的少量條目添加隨機正常量并將此矩陣連接回父族： ```py mutated_children = tf.add(children_after_sel, mutation_val_ph) # Combine children and parents into new population new_population = tf.concat(0, [parents, mutated_children]) ``` 1. 我們模型的最后一步是使用 TensorFlow 的`group()`操作將新種群分配給舊種群的變量： ```py step = tf.group(population.assign(new_population)) ``` 1. 我們現在可以初始化模型變量，如下所示： ```py init = tf.global_variables_initializer() sess.run(init) ``` 1. 最后，我們遍歷世代，重新創建隨機交叉和變異矩陣并更新每一代的人口： ```py for i in range(generations): # Create cross-over matrices for plugging in. crossover_mat = np.ones(shape=[num_children, features]) crossover_point = np.random.choice(np.arange(1, features-1, step=1), num_children) for pop_ix in range(num_children): crossover_mat[pop_ix,0:crossover_point[pop_ix]]=0\. # Generate mutation probability matrices mutation_prob_mat = np.random.uniform(size=[num_children, features]) mutation_values = np.random.normal(size=[num_children, features]) mutation_values[mutation_prob_mat >= mutation] = 0 # Run GA step feed_dict = {truth_ph: truth.reshape([1, features]), crossover_mat_ph: crossover_mat, mutation_val_ph: mutation_values} step.run(feed_dict, session=sess) best_individual_val = sess.run(best_individual, feed_dict=feed_dict) if i % 5 == 0: best_fit = sess.run(best_val, feed_dict = feed_dict) print('Generation: {}, Best Fitness (lowest MSE): {:.2}'.format(i, -best_fit)) ``` 1. 這導致以下輸出： ```py Generation: 0, Best Fitness (lowest MSE): 1.5 Generation: 5, Best Fitness (lowest MSE): 0.83 Generation: 10, Best Fitness (lowest MSE): 0.55 Generation: 185, Best Fitness (lowest MSE): 0.085 Generation: 190, Best Fitness (lowest MSE): 0.15 Generation: 195, Best Fitness (lowest MSE): 0.083 ``` ## 工作原理 在本文中，我們向您展示了如何使用 TensorFlow 運行簡單的遺傳算法。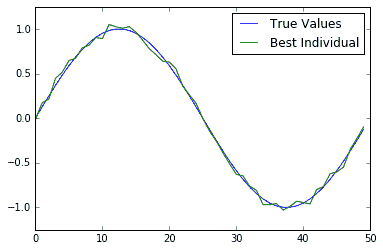為了驗證它是否有效，我們還可以在一個圖上查看最合適的個體解決方案和基本事實：  圖 4：200 代后的真實情況和最適合個體的繪圖圖。我們可以看到，最合適的個體非常接近真相 ## 更多 遺傳算法有許多變化。我們可以有兩個具有兩個不同適合度標準的父母群體（例如，最低 MSE 和平滑度）。我們可以對突變值施加限制，使其不大于 1 或小于-1。我們可以進行許多不同的更改，這些更改會有很大差異，具體取決于我們要優化的問題。對于這個人為的問題，很容易計算出適應度，但對于大多數遺傳算法來說，計算適應度是一項艱巨的任務。例如，如果我們想使用遺傳算法來優化卷積神經網絡的架構，我們可以讓個體成為參數數組。參數可以代表每個卷積層的濾波器大小，步幅大小等。這種個體的適應性將是在通過數據集的固定量的迭代之后的分類的準確率。如果我們在這個人口中有 100 個人，我們將不得不為每一代評估 100 個不同的 CNN 模型。這在計算上非常強烈。 在使用遺傳算法解決問題之前，明智的做法是弄清楚計算個體的`fitness`需要多長時間。如果此操作耗時，遺傳算法可能不是最佳使用工具。