# 實現邏輯回歸 對于這個秘籍，我們將實現邏輯回歸來預測樣本人群中低出生體重的概率。 ## 做好準備 邏輯回歸是將線性回歸轉換為二元分類的一種方法。這是通過將線性輸出轉換為 Sigmoid 函數來實現的，該函數將輸出在 0 和 1 之間進行縮放。目標是零或一，表示數據點是在一個類還是另一個類中。由于我們預測 0 和 1 之間的數字，如果預測高于指定的截止值，則預測被分類為類值 1，否則分類為 0。出于此示例的目的，我們將指定 cutoff 為 0.5，這將使分類像舍入輸出一樣簡單。 我們將用于此示例的數據將是從作者的 GitHub 倉庫獲得的低出生體重數據（ [https://github.com/nfmcclure/tensorflow_cookbook/raw/master/01_Introduction/07_Working_with_Data_Sources/birthweight_data/birthweight.dat](https://github.com/nfmcclure/tensorflow_cookbook/raw/master/01_Introduction/07_Working_with_Data_Sources/birthweight_data/birthweight.dat) ）。我們將從其他幾個因素預測低出生體重。 ## 操作步驟 我們按如下方式處理秘籍： 1. 我們首先加載庫，包括`request`庫，因為我們將通過超鏈接訪問低出生體重數據。我們還發起了一個會議： ```py import matplotlib.pyplot as plt import numpy as np import tensorflow as tf import requests from sklearn import datasets from sklearn.preprocessing import normalize from tensorflow.python.framework import ops ops.reset_default_graph() sess = tf.Session() ``` 1. 接下來，我們通過請求模塊加載數據并指定我們要使用的特征。我們必須具體，因為一個特征是實際出生體重，我們不想用它來預測出生體重是大于還是小于特定量。我們也不想將 ID 列用作預測器： ```py birth_weight_file = 'birth_weight.csv' # Download data and create data file if file does not exist in current directory if not os.path.exists(birth_weight_file): birthdata_url = 'https://github.com/nfmcclure/tensorflow_cookbook/raw/master/01_Introduction/07_Working_with_Data_Sources/birthweight_data/birthweight.dat' birth_file = requests.get(birthdata_url) birth_data = birth_file.text.split('\r\n') birth_header = birth_data[0].split('\t') birth_data = [[float(x) for x in y.split('\t') if len(x)>=1] for y in birth_data[1:] if len(y)>=1] with open(birth_weight_file, 'w', newline='') as f: writer = csv.writer(f) writer.writerow(birth_header) writer.writerows(birth_data) # Read birth weight data into memory birth_data = [] with open(birth_weight_file, newline='') as csvfile: csv_reader = csv.reader(csvfile) birth_header = next(csv_reader) for row in csv_reader: birth_data.append(row) birth_data = [[float(x) for x in row] for row in birth_data] # Pull out target variable y_vals = np.array([x[0] for x in birth_data]) # Pull out predictor variables (not id, not target, and not birthweight) x_vals = np.array([x[1:8] for x in birth_data]) ``` 1. 首先，我們將數據集拆分為測試和訓練集： ```py train_indices = np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False) test_indices = np.array(list(set(range(len(x_vals))) - set(train_indices))) x_vals_train = x_vals[train_indices] x_vals_test = x_vals[test_indices] y_vals_train = y_vals[train_indices] y_vals_test = y_vals[test_indices] ``` 1. 當特征在 0 和 1 之間縮放（最小 - 最大縮放）時，邏輯回歸收斂效果更好。那么，接下來我們將擴展每個特征： ```py def normalize_cols(m, col_min=np.array([None]), col_max=np.array([None])): if not col_min[0]: col_min = m.min(axis=0) if not col_max[0]: col_max = m.max(axis=0) return (m-col_min) / (col_max - col_min), col_min, col_max x_vals_train, train_min, train_max = np.nan_to_num(normalize_cols(x_vals_train)) x_vals_test = np.nan_to_num(normalize_cols(x_vals_test, train_min, train_max)) ``` > 請注意，在縮放數據集之前，我們將數據集拆分為 train 和 test。這是一個重要的區別。我們希望確保測試集完全不影響訓練集。如果我們在分裂之前縮放整個集合，那么我們不能保證它們不會相互影響。我們確保從訓練組中保存縮放以縮放測試集。 1. 接下來，我們聲明批量大小，占位符，變量和邏輯模型。我們不將輸出包裝在 sigmoid 中，因為該操作內置于 loss 函數中。另請注意，每次觀察都有七個輸入特征，因此`x_data`占位符的大小為`[None, 7]`。 ```py batch_size = 25 x_data = tf.placeholder(shape=[None, 7], dtype=tf.float32) y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32) A = tf.Variable(tf.random_normal(shape=[7,1])) b = tf.Variable(tf.random_normal(shape=[1,1])) model_output = tf.add(tf.matmul(x_data, A), b) ``` 1. 現在，我們聲明我們的損失函數，它具有 sigmoid 函數，初始化我們的變量，并聲明我們的優化函數： ```py loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(model_output, y_target)) init = tf.global_variables_initializer() sess.run(init) my_opt = tf.train.GradientDescentOptimizer(0.01) train_step = my_opt.minimize(loss) ``` 1. 在記錄損失函數的同時，我們還希望在訓練和測試集上記錄分類準確率。因此，我們將創建一個預測函數，返回任何大小的批量的準確率： ```py prediction = tf.round(tf.sigmoid(model_output)) predictions_correct = tf.cast(tf.equal(prediction, y_target), tf.float32) accuracy = tf.reduce_mean(predictions_correct) ``` 1. 現在，我們可以開始我們的訓練循環并記錄損失和準確率： ```py loss_vec = [] train_acc = [] test_acc = [] for i in range(1500): rand_index = np.random.choice(len(x_vals_train), size=batch_size) rand_x = x_vals_train[rand_index] rand_y = np.transpose([y_vals_train[rand_index]]) sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y}) temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y}) loss_vec.append(temp_loss) temp_acc_train = sess.run(accuracy, feed_dict={x_data: x_vals_train, y_target: np.transpose([y_vals_train])}) train_acc.append(temp_acc_train) temp_acc_test = sess.run(accuracy, feed_dict={x_data: x_vals_test, y_target: np.transpose([y_vals_test])}) test_acc.append(temp_acc_test) ``` 1. 以下是查看損失和準確率圖的代碼： ```py plt.plot(loss_vec, 'k-') plt.title('Cross' Entropy Loss per Generation') plt.xlabel('Generation') plt.ylabel('Cross' Entropy Loss') plt.show() plt.plot(train_acc, 'k-', label='Train Set Accuracy') plt.plot(test_acc, 'r--', label='Test Set Accuracy') plt.title('Train and Test Accuracy') plt.xlabel('Generation') plt.ylabel('Accuracy') plt.legend(loc='lower right') plt.show() ``` ## 工作原理 這是迭代和訓練和測試精度的損失。由于數據集僅為 189 次觀測，因此隨著數據集的隨機分裂，訓練和測試精度圖將發生變化。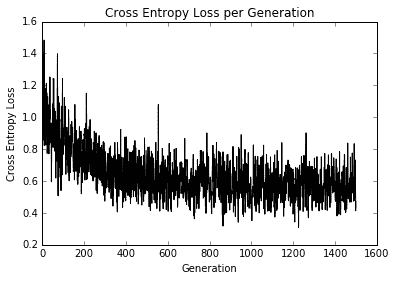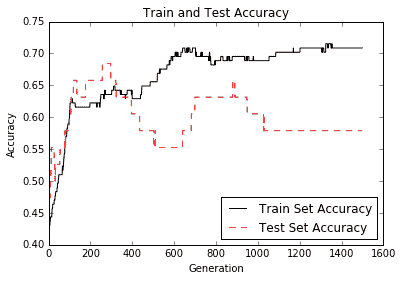第一個數字是交叉熵損失：  圖 11：在 1,500 次迭代過程中繪制的交叉熵損失 第二個圖顯示了訓練和測試裝置的準確率： Figure 12: Test and train set accuracy plotted over 1,500 generations