使用 Python 進行時間序列預測研究：法國香檳的月銷售額 · Machine Learning Mastery 博客文章翻譯

# 使用 Python 進行時間序列預測研究：法國香檳的月銷售額 > 原文： [https://machinelearningmastery.com/time-series-forecast-study-python-monthly-sales-french-champagne/](https://machinelearningmastery.com/time-series-forecast-study-python-monthly-sales-french-champagne/) 時間序列預測是一個過程，獲得良好預測的唯一方法是實施此過程。在本教程中，您將了解如何使用 Python 預測法國香檳的月銷售額。完成本教程將為您提供一個框架，用于處理您自己的時間序列預測問題的步驟和工具。完成本教程后，您將了解： * 如何確認您的 Python 環境并仔細定義時間序列預測問題。 * 如何創建測試工具來評估模型，開發基線預測，并使用時間序列分析工具更好地理解您的問題。 * 如何開發自回歸集成移動平均模型，將其保存到文件中，然后加載它以對新時間步驟進行預測。讓我們開始吧。 * **2017 年 3 月更新**：修復了“查看剩余錯誤”部分中運行錯誤模型的代碼示例中的拼寫錯誤。 ![Time Series Forecast Study with Python - Monthly Sales of French Champagne](https://img.kancloud.cn/23/6f/236f38f9ddac7eac61b952b9bc95481c_640x427.jpg) 使用 Python 進行時間序列預測研究 - 法國香檳的月銷售額 [Basheer Tome](https://www.flickr.com/photos/basheertome/5976017913/) 的照片，保留一些權利。 ## 概觀在本教程中，我們將完成從端到端的時間序列預測項目，從下載數據集并定義問題到訓練最終模型和進行預測。該項目并非詳盡無遺，但通過系統地處理時間序列預測問題，展示了如何快速獲得良好結果。我們將通過的這個項目的步驟如下。 1. 環境。 2. 問題描述。 3. 測試線束。 4. 持久性。 5. 數據分析。 6. ARIMA 模型。 7. 模型驗證。這將提供一個模板，用于處理您可以在自己的數據集上使用的時間序列預測問題。 ## 1.環境本教程假定已安裝且正在運行的 SciPy 環境和依賴項，包括： * SciPy 的 * NumPy 的 * Matplotlib * 熊貓 * scikit 學習 * statsmodels 如果您需要在工作站上安裝 Python 和 SciPy 環境的幫助，請考慮為您管理大部分內容的 [Anaconda 發行版](https://www.continuum.io/downloads)。此腳本將幫助您檢查這些庫的已安裝版本。 ```py # scipy import scipy print('scipy: %s' % scipy.__version__) # numpy import numpy print('numpy: %s' % numpy.__version__) # matplotlib import matplotlib print('matplotlib: %s' % matplotlib.__version__) # pandas import pandas print('pandas: %s' % pandas.__version__) # scikit-learn import sklearn print('sklearn: %s' % sklearn.__version__) # statsmodels import statsmodels print('statsmodels: %s' % statsmodels.__version__) ``` 用于編寫本教程的工作站上的結果如下： ```py scipy: 0.18.1 numpy: 1.11.2 matplotlib: 1.5.3 pandas: 0.19.1 sklearn: 0.18.1 statsmodels: 0.6.1 ``` ## 2.問題描述問題是要預測 Perrin Freres 標簽（以法國某個地區命名）的每月香檳銷售數量。該數據集提供了 1964 年 1 月至 1972 年 9 月的香檳月銷售數量，或者不到 10 年的數據。這些數值是數百萬銷售額，有 105 個觀察值。該數據集歸功于 Makridakis 和 Wheelwright，1989。 [您可以了解有關此數據集的更多信息，并直接從 DataMarket](https://datamarket.com/data/set/22r5/perrin-freres-monthly-champagne-sales-millions-64-72) 下載。將數據集下載為 CSV 文件，并將其放在當前工作目錄中，文件名為“ _champagne.csv_ ”。 ## 3.測試線束我們必須開發一個測試工具來研究數據并評估候選模型。這涉及兩個步驟： 1. 定義驗證數據集。 2. 開發模型評估方法。 ### 3.1 驗證數據集數據集不是最新的。這意味著我們無法輕松收集更新的數據來驗證模型。因此，我們將假裝它是 1971 年 9 月，并保留最后一年的分析和模型選擇數據。最后一年的數據將用于驗證最終模型。下面的代碼將數據集作為 Pandas 系列加載并分成兩部分，一部分用于模型開發（ _dataset.csv_ ），另一部分用于驗證（ _validation.csv_ ）。 ```py from pandas import Series series = Series.from_csv('champagne.csv', header=0) split_point = len(series) - 12 dataset, validation = series[0:split_point], series[split_point:] print('Dataset %d, Validation %d' % (len(dataset), len(validation))) dataset.to_csv('dataset.csv') validation.to_csv('validation.csv') ``` 運行該示例將創建兩個文件并打印每個文件中的觀察數。 ```py Dataset 93, Validation 12 ``` 這些文件的具體內容是： * _dataset.csv_ ：1964 年 1 月至 1971 年 9 月的觀察結果（93 次觀察） * _validation.csv_ ：1971 年 10 月至 1972 年 9 月的觀測（12 次觀測）驗證數據集約占原始數據集的 11％。請注意，保存的數據集沒有標題行，因此我們稍后在處理這些文件時無需滿足此要求。 ### 3.2。模型評估模型評估僅對上一節中準備的 _dataset.csv_ 中的數據進行。模型評估涉及兩個要素： 1. 表現指標。 2. 測試策略。 #### 3.2.1 績效衡量觀察結果是數百萬單位的香檳銷量。我們將使用均方根誤差（RMSE）來評估預測的表現。這將更加重視嚴重錯誤的預測，并且與原始數據具有相同的單位。在計算和報告 RMSE 之前，必須反轉對數據的任何變換，以使不同方法之間的表現直接相當。我們可以使用 scikit-learn 庫 _mean_squared_error（）_ 中的輔助函數計算 RMSE，它計算預期值列表（測試集）和預測列表之間的均方誤差。然后我們可以取這個值的平方根來給我們一個 RMSE 分數。例如： ```py from sklearn.metrics import mean_squared_error from math import sqrt ... test = ... predictions = ... mse = mean_squared_error(test, predictions) rmse = sqrt(mse) print('RMSE: %.3f' % rmse) ``` #### 3.2.2 測試策略候選模型將使用前向驗證進行評估。這是因為問題定義需要滾動預測類型模型。這是在給定所有可用數據的情況下需要一步預測的地方。前瞻性驗證將如下工作： * 數據集的前 50％將被阻止以訓練模型。 * 剩下的 50％的數據集將被迭代并測試模型。 * 對于測試數據集中的每個步驟： * 將訓練模型。 * 進行一步預測并存儲預測以供以后評估。 * 來自測試數據集的實際觀察將被添加到訓練數據集中以用于下一次迭代。 * 將評估在測試數據集的迭代期間做出的預測并報告 RMSE 分數。鑒于數據的小尺寸，我們將允許在每次預測之前根據所有可用數據重新訓練模型。我們可以使用簡單的 NumPy 和 Python 代碼編寫測試工具的代碼。首先，我們可以直接將數據集拆分為訓練集和測試集。如果加載的數據仍然有一些 _String_ 或 _Integer_ 數據類型，我們小心地始終將加載的數據集轉換為 _float32_ 。 ```py # prepare data X = series.values X = X.astype('float32') train_size = int(len(X) * 0.50) train, test = X[0:train_size], X[train_size:] ``` 接下來，我們可以迭代測試數據集中的時間步長。訓練數據集存儲在 Python 列表中，因為我們需要在每次迭代時輕松附加新的觀察結果，并且 NumPy 數組連接感覺有點矯枉過正。由于結果或觀察被稱為 _y_ 和 _，_（a' _y []，所以該模型所做的預測被稱為 _yhat_ 。帶有上述標記的 HTG7]是用于預測 _y_ 變量的數學符號。_ 如果模型存在問題，則在每個觀察中打印預測和觀察以進行健全性檢查預測。 ```py # walk-forward validation history = [x for x in train] predictions = list() for i in range(len(test)): # predict yhat = ... predictions.append(yhat) # observation obs = test[i] history.append(obs) print('>Predicted=%.3f, Expected=%3.f' % (yhat, obs)) ``` ## 堅持不懈在陷入數據分析和建模之前的第一步是建立表現基準。這將提供用于使用所提出的測試工具評估模型的模板和用于比較所有更精細的預測模型的表現測量。時間序列預測的基線預測稱為樸素預測或持久性。這是來自前一時間步驟的觀察被用作下一時間步驟的觀察預測的地方。我們可以將其直接插入上一節中定義的測試工具中。完整的代碼清單如下。 ```py from pandas import Series from sklearn.metrics import mean_squared_error from math import sqrt # load data series = Series.from_csv('dataset.csv') # prepare data X = series.values X = X.astype('float32') train_size = int(len(X) * 0.50) train, test = X[0:train_size], X[train_size:] # walk-forward validation history = [x for x in train] predictions = list() for i in range(len(test)): # predict yhat = history[-1] predictions.append(yhat) # observation obs = test[i] history.append(obs) print('>Predicted=%.3f, Expected=%3.f' % (yhat, obs)) # report performance mse = mean_squared_error(test, predictions) rmse = sqrt(mse) print('RMSE: %.3f' % rmse) ``` 運行測試工具會為測試數據集的每次迭代打印預測和觀察。該示例以打印模型的 RMSE 結束。在這種情況下，我們可以看到持久性模型實現了 3186.501 的 RMSE。這意味著平均而言，每個預測的銷售額約為 31.66 億美元。 ```py ... >Predicted=4676.000, Expected=5010 >Predicted=5010.000, Expected=4874 >Predicted=4874.000, Expected=4633 >Predicted=4633.000, Expected=1659 >Predicted=1659.000, Expected=5951 RMSE: 3186.501 ``` 我們現在有一個基線預測方法和表現;現在我們可以開始挖掘我們的數據了。 ## 5.數據分析我們可以使用匯總統計數據和數據圖來快速了解有關預測問題結構的更多信息。在本節中，我們將從五個角度來看待數據： 1. 摘要統計。 2. 線圖。 3. 季節線圖 4. 密度圖。 5. 盒子和晶須圖。 ### 5.1 摘要統計摘要統計信息可快速查看觀察值的限制。它可以幫助您快速了解我們正在使用的內容。以下示例計算并打印時間序列的摘要統計信息。 ```py from pandas import Series series = Series.from_csv('dataset.csv') print(series.describe()) ``` 運行該示例提供了許多要查看的摘要統計信息。這些統計數據的一些觀察包括： * 觀察數量（計數）符合我們的預期，這意味著我們正確處理數據。 * 平均值約為 4,641，我們可能會考慮這個系列中的水平。 * 標準偏差（平均值的平均值差異）相對較大，為 2,486 個銷售額。 * 百分位數和標準偏差確實表明數據的大量傳播。 ```py count 93.000000 mean 4641.118280 std 2486.403841 min 1573.000000 25% 3036.000000 50% 4016.000000 75% 5048.000000 max 13916.000000 ``` ### 5.2 線圖時間序列的線圖可以提供對問題的大量洞察。下面的示例創建并顯示數據集的線圖。 ```py from pandas import Series from matplotlib import pyplot series = Series.from_csv('dataset.csv') series.plot() pyplot.show() ``` 運行示例并查看繪圖。注意系列中任何明顯的時間結構。該圖的一些觀察結果包括： * 隨著時間的推移，銷售可能會有增加的趨勢。 * 每年的銷售似乎都有系統的季節性。 * 季節性信號似乎隨著時間的推移而增長，表明存在乘法關系（增加變化）。 * 似乎沒有任何明顯的異常值。 * 季節性表明該系列幾乎肯定是非靜止的。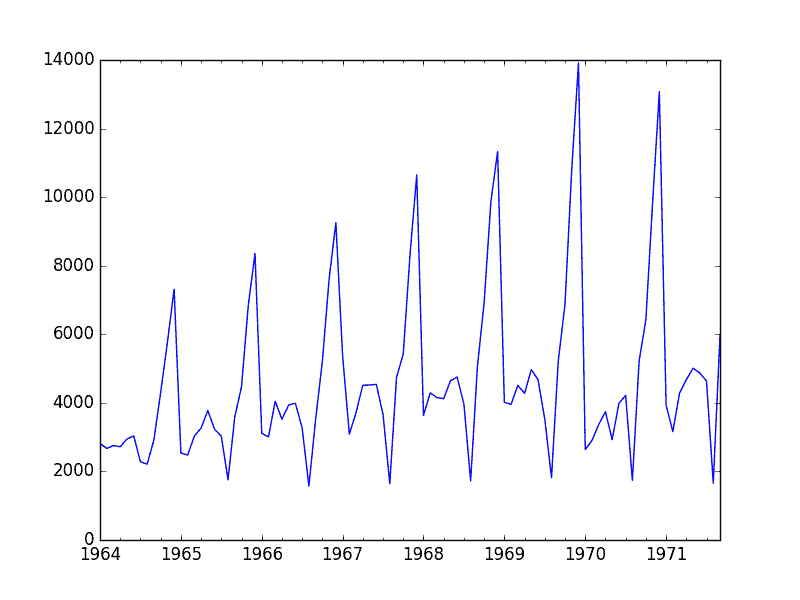 ![Champagne Sales Line Plot](https://img.kancloud.cn/65/ac/65ac48ab0200455357ea74a9f20cb9a5_800x600.jpg) 香檳銷售線圖明確建模季節性組件并將其刪除可能會有好處。您還可以探索使用一個或兩個級別的差分，以使系列靜止。季節性成分的增加趨勢或增長可能表明使用對數或其他功率變換。 ### 5.3 季節線圖我們可以通過逐年觀察數據集的線圖來確認季節性是一個年度周期的假設。下面的示例將 7 個完整年份的數據作為單獨的組，并為每個數據創建一個線圖。線圖垂直對齊，以幫助發現任何逐年模式。 ```py from pandas import Series from pandas import DataFrame from pandas import TimeGrouper from matplotlib import pyplot series = Series.from_csv('dataset.csv') groups = series['1964':'1970'].groupby(TimeGrouper('A')) years = DataFrame() pyplot.figure() i = 1 n_groups = len(groups) for name, group in groups: pyplot.subplot((n_groups*100) + 10 + i) i += 1 pyplot.plot(group) pyplot.show() ``` 運行該示例將創建 7 個線圖的堆棧。我們可以清楚地看到每年八月下降，并從每年八月到十二月上升。盡管處于不同的水平，但這種模式每年看起來都是一樣的。這將有助于以后任何明確的基于季節的建模。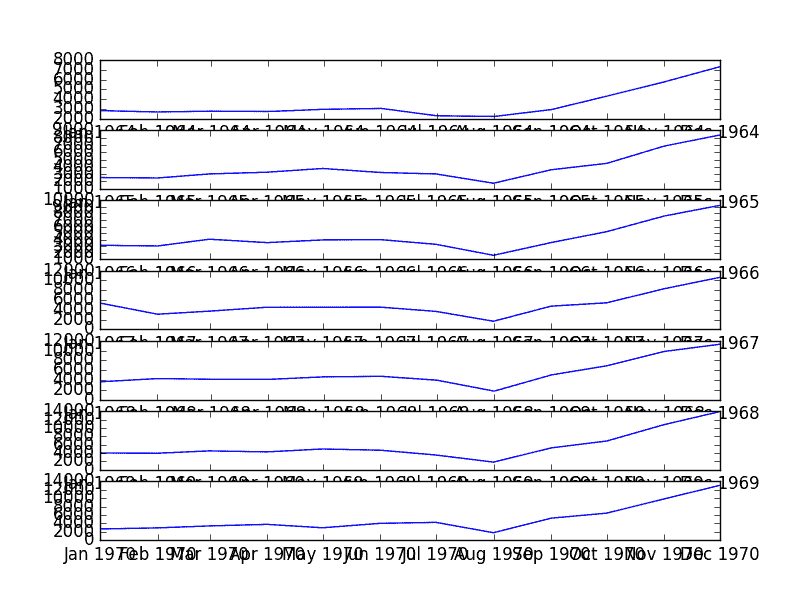 ![Seasonal Per Year Line Plots](https://img.kancloud.cn/d8/57/d857178b85b05564b3a4767947301235_800x600.jpg) 每年季節性線圖如果將所有季節線圖添加到一個圖中以幫助對比每年的數據，可能會更容易。 ### 5.4 密度圖回顧觀察密度圖可以進一步了解數據結構。下面的示例創建了沒有任何時間結構的觀測的直方圖和密度圖。 ```py from pandas import Series from matplotlib import pyplot series = Series.from_csv('dataset.csv') pyplot.figure(1) pyplot.subplot(211) series.hist() pyplot.subplot(212) series.plot(kind='kde') pyplot.show() ``` 運行示例并查看繪圖。這些情節的一些觀察包括： * 分布不是高斯分布。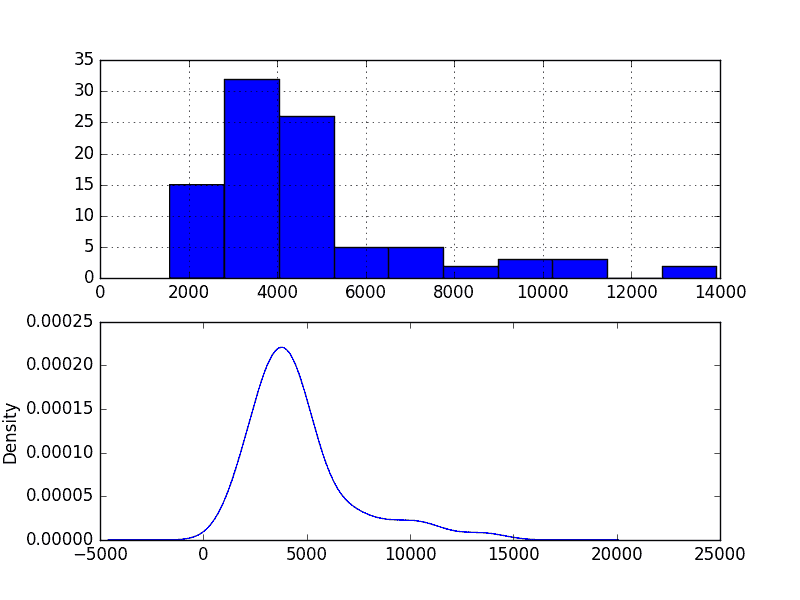 * 形狀具有長的右尾并且可以表示指數分布 ![](https://img.kancloud.cn/cb/2f/cb2f5c4d740887a946b1cd6071712e08_800x600.jpg) 這為在建模之前探索數據的一些功率變換提供了更多支持。 ### 5.5 盒子和晶須圖我們可以按月對月度數據進行分組，并了解每年的觀察結果的傳播情況以及這種情況可能會如何變化。我們確實希望看到一些趨勢（增加平均值或中位數），但看看分布的其他部分可能會如何變化可能會很有趣。下面的例子按年份對觀測值進行分組，并為每年的觀測值創建一個方框和胡須圖。去年（1971 年）僅包含 9 個月，與其他年份的 12 個月觀察結果可能無差別。因此，僅繪制了 1964 年至 1970 年之間的數據。 ```py from pandas import Series from pandas import DataFrame from pandas import TimeGrouper from matplotlib import pyplot series = Series.from_csv('dataset.csv') groups = series['1964':'1970'].groupby(TimeGrouper('A')) years = DataFrame() for name, group in groups: years[name.year] = group.values years.boxplot() pyplot.show() ``` 運行該示例并排創建 7 個框和胡須圖，每 7 年選擇一個數據。審查這些圖的一些觀察結果包括： * 每年的中值（紅線）可能會呈現增長趨勢。 * 差價或中間 50％的數據（藍框）確實看起來相當穩定。 * 每年都有異常值（黑色十字架）;這些可能是季節性周期的頂部或底部。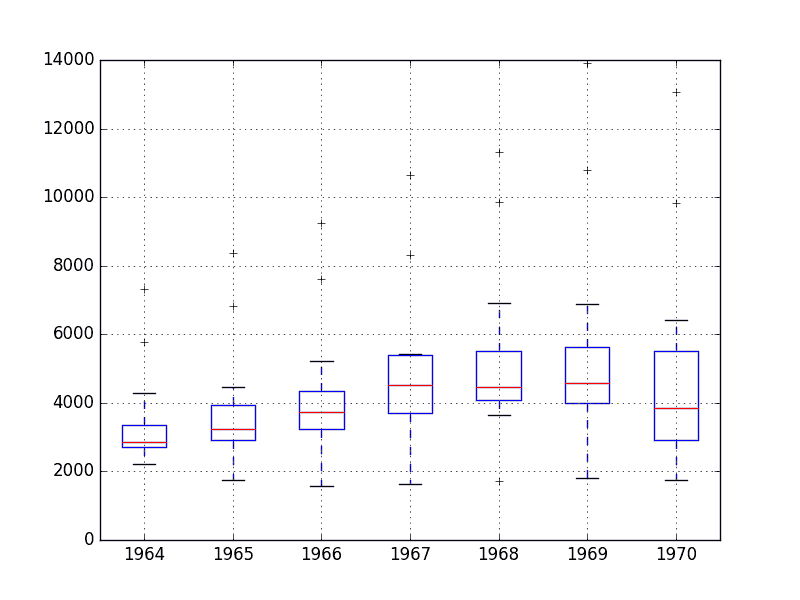 * 1970 年的最后一年確實與前幾年的趨勢不同 ![Champagne Sales Box and Whisker Plots](https://img.kancloud.cn/42/bb/42bb3d84288498b31c0dfd4c2922334b_800x600.jpg) 香檳銷售盒和晶須圖這些觀察結果表明，這些年可能出現一些增長趨勢，而異常值可能是季節周期的一部分。這種年度數據視圖是一個有趣的途徑，可以通過查看逐年的摘要統計數據和每年的摘要統計數據的變化來進一步追求。 ## 6\. ARIMA 模型在本節中，我們將針對該問題開發自回歸集成移動平均線（ARIMA）模型。我們將通過手動和自動配置 ARIMA 模型來進行建模。接下來是調查所選模型的殘差的第三步。因此，本節分為 3 個步驟： 1. 手動配置 ARIMA。 2. 自動配置 ARIMA。 3. 查看殘留錯誤。 ### 6.1 手動配置 ARIMA ARIMA（ _p，d，q_ ）模型需要三個參數，并且傳統上是手動配置的。對時間序列數據的分析假設我們正在使用固定的時間序列。時間序列幾乎肯定是非平穩的。我們可以通過首先對系列進行差分并使用統計檢驗確認結果是靜止的來使其靜止。該系列的季節性似乎是逐年的。季節性數據可以通過從前一周期中的同一時間減去觀察值來區分，在這種情況下是前一年的同一月份。這確實意味著我們將失去第一年的觀察，因為沒有前一年的差異。下面的示例創建該系列的延長版本并將其保存到文件 _stationary.csv_ 。 ```py from pandas import Series from statsmodels.tsa.stattools import adfuller from matplotlib import pyplot # create a differenced series def difference(dataset, interval=1): diff = list() for i in range(interval, len(dataset)): value = dataset[i] - dataset[i - interval] diff.append(value) return Series(diff) series = Series.from_csv('dataset.csv') X = series.values X = X.astype('float32') # difference data months_in_year = 12 stationary = difference(X, months_in_year) stationary.index = series.index[months_in_year:] # check if stationary result = adfuller(stationary) print('ADF Statistic: %f' % result[0]) print('p-value: %f' % result[1]) print('Critical Values:') for key, value in result[4].items(): print('\t%s: %.3f' % (key, value)) # save stationary.to_csv('stationary.csv') # plot stationary.plot() pyplot.show() ``` 運行該示例輸出差異系列是否靜止的統計顯著性檢驗的結果。具體來說，增強 Dickey-Fuller 測試。結果表明，檢驗統計值-7.134898 小于-3.515 的 1％的臨界值。這表明我們可以拒絕具有小于 1％的顯著性水平的零假設（即，結果是統計僥幸的低概率）。拒絕原假設意味著該過程沒有單位根，反過來，時間序列是靜止的或沒有時間依賴的結構。 ```py ADF Statistic: -7.134898 p-value: 0.000000 Critical Values: 5%: -2.898 1%: -3.515 10%: -2.586 ``` 作為參考，可以通過添加前一年的同一月份的觀察來反轉季節性差異操作。在通過適合季節性差異數據的模型進行預測的情況下需要這樣做。下面列出了反轉季節性差異操作的功能的完整性。 ```py # invert differenced value def inverse_difference(history, yhat, interval=1): return yhat + history[-interval] ``` 還創建了差異數據集的圖。該圖未顯示任何明顯的季節性或趨勢，表明季節性差異的數據集是建模的良好起點。我們將使用此數據集作為 ARIMA 模型的輸入。它還表明不需要進一步的差分，并且 d 參數可以設置為 0。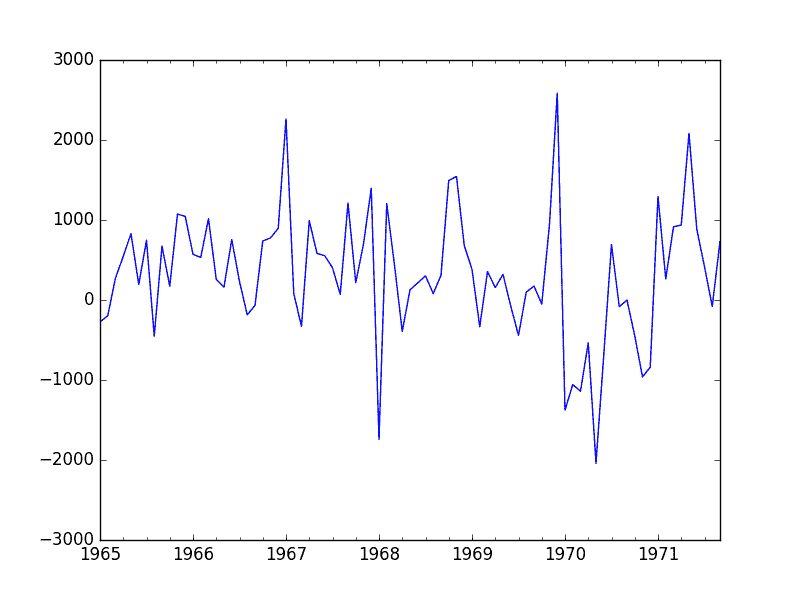 ![Seasonal Differenced Champagne Sales Line Plot](https://img.kancloud.cn/df/00/df006cd88321a6819ac1dea368e81acf_800x600.jpg) 季節性差異香檳銷售線圖下一步是分別選擇自回歸（AR）和移動平均（MA）參數， _p_ 和 _q_ 的滯后值。我們可以通過查看自相關函數（ACF）和部分自相關函數（PACF）圖來做到這一點。注意，我們現在使用季節性差異的 stationary.csv 作為我們的數據集。下面的示例為該系列創建了 ACF 和 PACF 圖。 ```py from pandas import Series from statsmodels.graphics.tsaplots import plot_acf from statsmodels.graphics.tsaplots import plot_pacf from matplotlib import pyplot series = Series.from_csv('stationary.csv') pyplot.figure() pyplot.subplot(211) plot_acf(series, ax=pyplot.gca()) pyplot.subplot(212) plot_pacf(series, ax=pyplot.gca()) pyplot.show() ``` 運行該示例并查看繪圖，以獲得有關如何為 ARIMA 模型設置 _p_ 和 _q_ 變量的見解。以下是該圖的一些觀察結果。 * ACF 顯示 1 個月的顯著滯后。 * PACF 顯示 1 個月的顯著滯后，在 12 個月和 13 個月可能有一些顯著的滯后。 * ACF 和 PACF 都在同一點下降，可能表明 AR 和 MA 的混合。 p 和 q 值的良好起點也是 1。 PACF 圖還表明差異數據中仍存在一些季節性。我們可能會考慮更好的季節性模型，例如直接建模并明確地將其從模型中移除而不是季節性差異。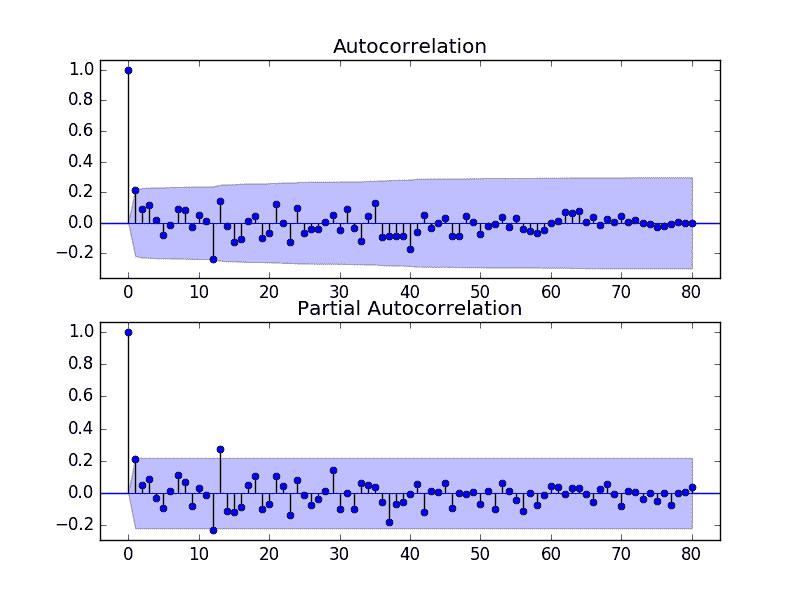 ![ACF and PACF Plots of Seasonally Differenced Champagne Sales](https://img.kancloud.cn/0c/27/0c27b0a3049892d7ae7bd3e767c8351e_800x600.jpg) ACF 和 PACF 季節性差異香檳銷售情節這種快速分析表明固定數據上的 ARIMA（1,0,1）可能是一個很好的起點。在擬合每個 ARIMA 模型之前，歷史觀察將在季節上有所不同。對于所有預測，差異將被反轉，以使它們與原始銷售計數單位中的預期觀察直接相當。實驗表明，ARIMA 的這種配置不會收斂并導致底層庫出錯。進一步的實驗表明，在靜止數據中增加一級差分使模型更穩定。該模型可以擴展到 ARIMA（1,1,1）。我們還將禁用從模型中自動添加趨勢常數，方法是將'_ 趨勢 _'參數設置為' _nc_ '，以便在調用 [fit（）時沒有常數](http://statsmodels.sourceforge.net/stable/generated/statsmodels.tsa.arima_model.ARIMA.fit.html)。通過實驗，我發現這可以在某些問題上產生更好的預測表現。下面的示例演示了此 ARIMA 模型在測試工具上的表現。 ```py from pandas import Series from sklearn.metrics import mean_squared_error from statsmodels.tsa.arima_model import ARIMA from math import sqrt # create a differenced series def difference(dataset, interval=1): diff = list() for i in range(interval, len(dataset)): value = dataset[i] - dataset[i - interval] diff.append(value) return diff # invert differenced value def inverse_difference(history, yhat, interval=1): return yhat + history[-interval] # load data series = Series.from_csv('dataset.csv') # prepare data X = series.values X = X.astype('float32') train_size = int(len(X) * 0.50) train, test = X[0:train_size], X[train_size:] # walk-forward validation history = [x for x in train] predictions = list() for i in range(len(test)): # difference data months_in_year = 12 diff = difference(history, months_in_year) # predict model = ARIMA(diff, order=(1,1,1)) model_fit = model.fit(trend='nc', disp=0) yhat = model_fit.forecast()[0] yhat = inverse_difference(history, yhat, months_in_year) predictions.append(yhat) # observation obs = test[i] history.append(obs) print('>Predicted=%.3f, Expected=%3.f' % (yhat, obs)) # report performance mse = mean_squared_error(test, predictions) rmse = sqrt(mse) print('RMSE: %.3f' % rmse) ``` 注意，您可能會看到來自底層線性代數庫的警告消息;現在可以忽略這一點。運行此示例會導致 RMSE 為 956.942，這明顯優于 3186.501 的持久性 RMSE。 ```py ... >Predicted=3157.018, Expected=5010 >Predicted=4615.082, Expected=4874 >Predicted=4624.998, Expected=4633 >Predicted=2044.097, Expected=1659 >Predicted=5404.428, Expected=5951 RMSE: 956.942 ``` 這是一個很好的開始，但我們可以通過更好的配置 ARIMA 模型獲得改進的結果。 ### 6.2 網格搜索 ARIMA 超參數 ACF 和 PACF 圖顯示 ARIMA（1,0,1）或類似物可能是我們能做的最好的。為了確認這一分析，我們可以對一套 ARIMA 超參數進行網格搜索，并檢查沒有模型可以獲得更好的樣本外 RMSE 表現。在本節中，我們將搜索組合的 _p_ ， _d_ 和 _q_ 的值（跳過那些未收斂的組合），并找到結果的組合在測試集上的最佳表現。我們將使用網格搜索來探索整數值子集中的所有組合。具體來說，我們將搜索以下參數的所有組合： * _p_ ：0 至 6。 * _d_ ：0 到 2。 * _q_ ：0 到 6。這是（ _7 * 3 * 7_ ）或 147，測試工具的潛在運行并且將花費一些時間來執行。評估具有 12 或 13 滯后的 MA 模型可能是有趣的，因為通過回顧 ACF 和 PACF 圖可能會感興趣。實驗表明這些模型可能不穩定，導致基礎數學庫中的錯誤。下面列出了測試工具的網格搜索版本的完整工作示例。 ```py import warnings from pandas import Series from statsmodels.tsa.arima_model import ARIMA from sklearn.metrics import mean_squared_error from math import sqrt import numpy # create a differenced series def difference(dataset, interval=1): diff = list() for i in range(interval, len(dataset)): value = dataset[i] - dataset[i - interval] diff.append(value) return numpy.array(diff) # invert differenced value def inverse_difference(history, yhat, interval=1): return yhat + history[-interval] # evaluate an ARIMA model for a given order (p,d,q) and return RMSE def evaluate_arima_model(X, arima_order): # prepare training dataset X = X.astype('float32') train_size = int(len(X) * 0.50) train, test = X[0:train_size], X[train_size:] history = [x for x in train] # make predictions predictions = list() for t in range(len(test)): # difference data months_in_year = 12 diff = difference(history, months_in_year) model = ARIMA(diff, order=arima_order) model_fit = model.fit(trend='nc', disp=0) yhat = model_fit.forecast()[0] yhat = inverse_difference(history, yhat, months_in_year) predictions.append(yhat) history.append(test[t]) # calculate out of sample error mse = mean_squared_error(test, predictions) rmse = sqrt(mse) return rmse # evaluate combinations of p, d and q values for an ARIMA model def evaluate_models(dataset, p_values, d_values, q_values): dataset = dataset.astype('float32') best_score, best_cfg = float("inf"), None for p in p_values: for d in d_values: for q in q_values: order = (p,d,q) try: mse = evaluate_arima_model(dataset, order) if mse < best_score: best_score, best_cfg = mse, order print('ARIMA%s RMSE=%.3f' % (order,mse)) except: continue print('Best ARIMA%s RMSE=%.3f' % (best_cfg, best_score)) # load dataset series = Series.from_csv('dataset.csv') # evaluate parameters p_values = range(0, 7) d_values = range(0, 3) q_values = range(0, 7) warnings.filterwarnings("ignore") evaluate_models(series.values, p_values, d_values, q_values) ``` 運行該示例將遍歷所有組合，并在收斂且無錯誤的情況下報告結果。該示例需要 2 分多鐘才能在現代硬件上運行。結果顯示，發現的最佳配置是 ARIMA（0,0,1），RMSE 為 939.464，略低于上一節中手動配置的 ARIMA。這種差異可能是也可能不具有統計學意義。 ```py ... ARIMA(5, 1, 2) RMSE=1003.200 ARIMA(5, 2, 1) RMSE=1053.728 ARIMA(6, 0, 0) RMSE=996.466 ARIMA(6, 1, 0) RMSE=1018.211 ARIMA(6, 1, 1) RMSE=1023.762 Best ARIMA(0, 0, 1) RMSE=939.464 ``` 我們將繼續選擇這個 ARIMA（0,0,1）模型。 ### 6.3 查看殘留錯誤對模型進行良好的最終檢查是檢查殘差預測誤差。理想情況下，殘差的分布應該是具有零均值的高斯分布。我們可以使用匯總統計和圖來檢查這一點，以調查 ARIMA（0,0,1）模型中的殘差。以下示例計算并總結了殘差預測誤差。 ```py from pandas import Series from pandas import DataFrame from statsmodels.tsa.arima_model import ARIMA from matplotlib import pyplot # create a differenced series def difference(dataset, interval=1): diff = list() for i in range(interval, len(dataset)): value = dataset[i] - dataset[i - interval] diff.append(value) return diff # invert differenced value def inverse_difference(history, yhat, interval=1): return yhat + history[-interval] # load data series = Series.from_csv('dataset.csv') # prepare data X = series.values X = X.astype('float32') train_size = int(len(X) * 0.50) train, test = X[0:train_size], X[train_size:] # walk-forward validation history = [x for x in train] predictions = list() for i in range(len(test)): # difference data months_in_year = 12 diff = difference(history, months_in_year) # predict model = ARIMA(diff, order=(0,0,1)) model_fit = model.fit(trend='nc', disp=0) yhat = model_fit.forecast()[0] yhat = inverse_difference(history, yhat, months_in_year) predictions.append(yhat) # observation obs = test[i] history.append(obs) # errors residuals = [test[i]-predictions[i] for i in range(len(test))] residuals = DataFrame(residuals) print(residuals.describe()) # plot pyplot.figure() pyplot.subplot(211) residuals.hist(ax=pyplot.gca()) pyplot.subplot(212) residuals.plot(kind='kde', ax=pyplot.gca()) pyplot.show() ``` 首先運行該示例描述了殘差的分布。我們可以看到分布具有正確的偏移，并且平均值在 165.904728 處非零。這或許表明預測存在偏見。 ```py count 47.000000 mean 165.904728 std 934.696199 min -2164.247449 25% -289.651596 50% 191.759548 75% 732.992187 max 2367.304748 ``` 還繪制了殘差的分布。這些圖表顯示了具有崎嶇左尾的類高斯分布，進一步證明了可能值得探索的功率變換。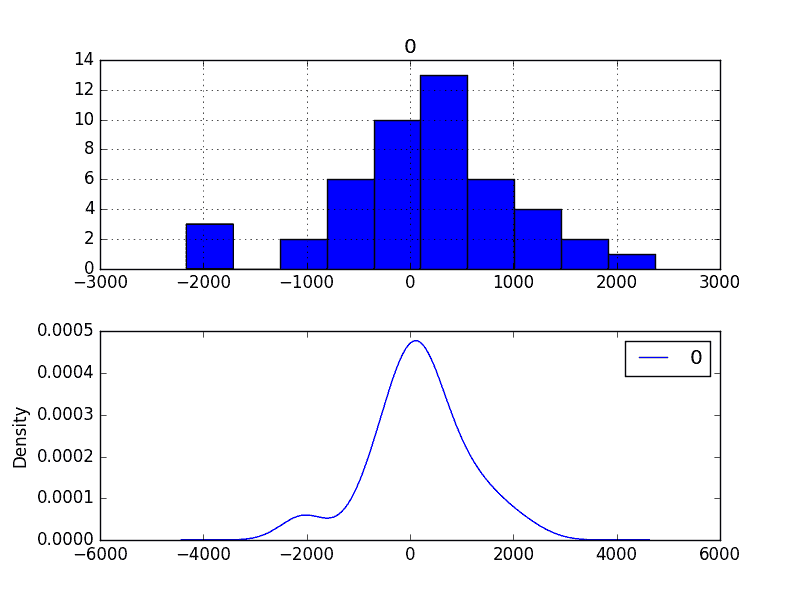 ![Residual Forecast Error Density Plots](https://img.kancloud.cn/b4/1c/b41c757a211f9f28b440d9a0c4f14b29_800x600.jpg) 剩余預測誤差密度圖我們可以通過將每個預測的平均殘差 165.904728 添加到偏差校正預測來使用此信息。以下示例執行此偏差關聯。 ```py from pandas import Series from pandas import DataFrame from statsmodels.tsa.arima_model import ARIMA from matplotlib import pyplot from sklearn.metrics import mean_squared_error from math import sqrt # create a differenced series def difference(dataset, interval=1): diff = list() for i in range(interval, len(dataset)): value = dataset[i] - dataset[i - interval] diff.append(value) return diff # invert differenced value def inverse_difference(history, yhat, interval=1): return yhat + history[-interval] # load data series = Series.from_csv('dataset.csv') # prepare data X = series.values X = X.astype('float32') train_size = int(len(X) * 0.50) train, test = X[0:train_size], X[train_size:] # walk-forward validation history = [x for x in train] predictions = list() bias = 165.904728 for i in range(len(test)): # difference data months_in_year = 12 diff = difference(history, months_in_year) # predict model = ARIMA(diff, order=(0,0,1)) model_fit = model.fit(trend='nc', disp=0) yhat = model_fit.forecast()[0] yhat = bias + inverse_difference(history, yhat, months_in_year) predictions.append(yhat) # observation obs = test[i] history.append(obs) # report performance mse = mean_squared_error(test, predictions) rmse = sqrt(mse) print('RMSE: %.3f' % rmse) # errors residuals = [test[i]-predictions[i] for i in range(len(test))] residuals = DataFrame(residuals) print(residuals.describe()) # plot pyplot.figure() pyplot.subplot(211) residuals.hist(ax=pyplot.gca()) pyplot.subplot(212) residuals.plot(kind='kde', ax=pyplot.gca()) pyplot.show() ``` 預測的表現從 939.464 略微改善至 924.699，這可能是也可能不是很重要。預測殘差的總結表明，平均值確實被移動到非常接近零的值。 ```py RMSE: 924.699 count 4.700000e+01 mean 4.965016e-07 std 9.346962e+02 min -2.330152e+03 25% -4.555563e+02 50% 2.585482e+01 75% 5.670875e+02 max 2.201400e+03 ``` 最后，剩余誤差的密度圖確實顯示向零的小偏移。這種偏差校正是否值得，值得商榷，但我們現在將使用它。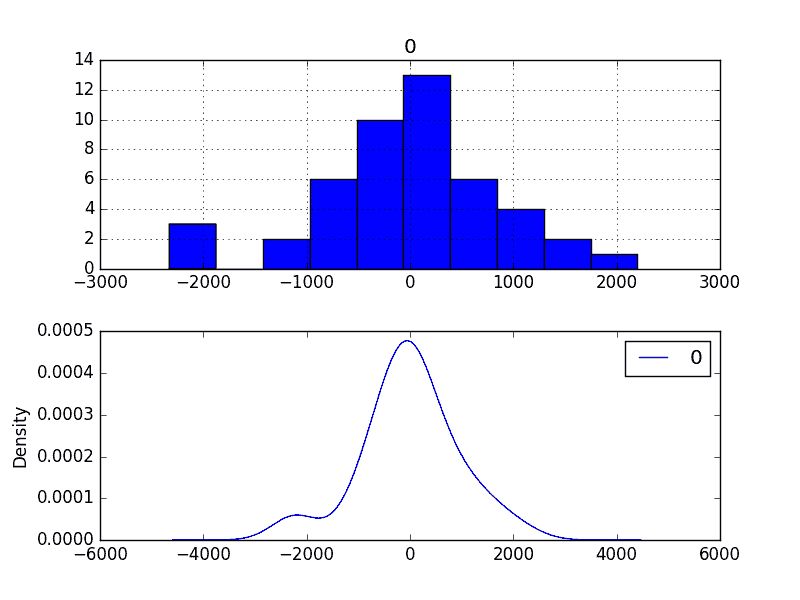 ![Bias Corrected Residual Forecast Error Density Plots](https://img.kancloud.cn/b6/e0/b6e04a997c5644625dc72d5e6174acfa_800x600.jpg) 偏差校正殘差預測誤差密度圖檢查任何類型的自相關的殘差的時間序列也是一個好主意。如果存在，則表明該模型有更多機會對數據中的時間結構進行建模。下面的示例重新計算殘差，并創建 ACF 和 PACF 圖以檢查是否存在任何顯著的自相關。 ```py from pandas import Series from pandas import DataFrame from statsmodels.tsa.arima_model import ARIMA from matplotlib import pyplot from statsmodels.graphics.tsaplots import plot_acf from statsmodels.graphics.tsaplots import plot_pacf # create a differenced series def difference(dataset, interval=1): diff = list() for i in range(interval, len(dataset)): value = dataset[i] - dataset[i - interval] diff.append(value) return diff # invert differenced value def inverse_difference(history, yhat, interval=1): return yhat + history[-interval] # load data series = Series.from_csv('dataset.csv') # prepare data X = series.values X = X.astype('float32') train_size = int(len(X) * 0.50) train, test = X[0:train_size], X[train_size:] # walk-forward validation history = [x for x in train] predictions = list() for i in range(len(test)): # difference data months_in_year = 12 diff = difference(history, months_in_year) # predict model = ARIMA(diff, order=(0,0,1)) model_fit = model.fit(trend='nc', disp=0) yhat = model_fit.forecast()[0] yhat = inverse_difference(history, yhat, months_in_year) predictions.append(yhat) # observation obs = test[i] history.append(obs) # errors residuals = [test[i]-predictions[i] for i in range(len(test))] residuals = DataFrame(residuals) print(residuals.describe()) # plot pyplot.figure() pyplot.subplot(211) plot_acf(residuals, ax=pyplot.gca()) pyplot.subplot(212) plot_pacf(residuals, ax=pyplot.gca()) pyplot.show() ``` 結果表明，該模型捕獲了時間序列中存在的小自相關。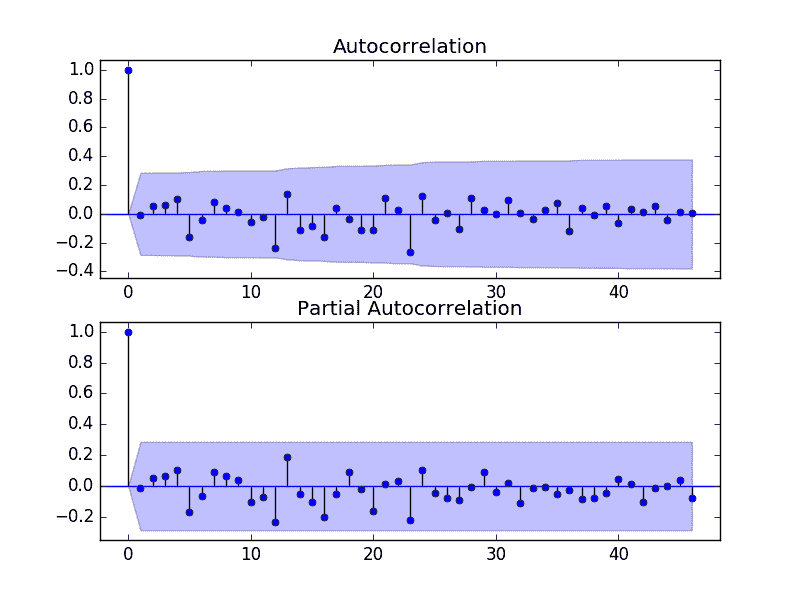 ![Residual Forecast Error ACF and PACF Plots](https://img.kancloud.cn/c8/dc/c8dca865e38263c8b13459769c2c643a_800x600.jpg) 剩余預測誤差 ACF 和 PACF 圖 ## 7.模型驗證在開發模型并選擇最終模型后，必須對其進行驗證和最終確定。驗證是流程的一個可選部分，但提供“最后檢查”以確保我們沒有被欺騙或誤導自己。本節包括以下步驟： 1. **Finalize Model** ：訓練并保存最終模型。 2. **進行預測**：加載最終模型并進行預測。 3. **驗證模型**：加載并驗證最終模型。 ### 7.1 完成模型最終確定模型涉及在整個數據集上擬合 ARIMA 模型，在這種情況下，在整個數據集的變換版本上。一旦適合，模型可以保存到文件中供以后使用。下面的示例在數據集上訓練 ARIMA（0,0,1）模型，并將整個擬合對象和偏差保存到文件中。當前穩定版本的 statsmodels 庫（v0.6.1）中存在一個錯誤，當您嘗試從文件加載已保存的 ARIMA 模型時會導致錯誤。報告的錯誤是： ```py TypeError: __new__() takes at least 3 arguments (1 given) ``` 當我測試它時，這個 bug 似乎也出現在 statsmodels 的 0.8 版本候選版本 1 中。有關詳細信息，請參閱 [Zae Myung Kim](http://zaemyung.com/) 的[討論并修復此 GitHub 問題](https://github.com/statsmodels/statsmodels/pull/3217)。我們可以使用一個猴子補丁來解決這個問題，該補丁在保存之前將 ___getnewargs __（）_ 實例函數添加到 ARIMA 類。下面的示例將擬合模型保存到正確狀態的文件，以便以后可以成功加載。 ```py from pandas import Series from statsmodels.tsa.arima_model import ARIMA from scipy.stats import boxcox import numpy # monkey patch around bug in ARIMA class def __getnewargs__(self): return ((self.endog),(self.k_lags, self.k_diff, self.k_ma)) ARIMA.__getnewargs__ = __getnewargs__ # create a differenced series def difference(dataset, interval=1): diff = list() for i in range(interval, len(dataset)): value = dataset[i] - dataset[i - interval] diff.append(value) return diff # load data series = Series.from_csv('dataset.csv') # prepare data X = series.values X = X.astype('float32') # difference data months_in_year = 12 diff = difference(X, months_in_year) # fit model model = ARIMA(diff, order=(0,0,1)) model_fit = model.fit(trend='nc', disp=0) # bias constant, could be calculated from in-sample mean residual bias = 165.904728 # save model model_fit.save('model.pkl') numpy.save('model_bias.npy', [bias]) ``` 運行該示例將創建兩個本地文件： * _model.pkl_ 這是調用 _ARIMA.fit（）_ 的 ARIMAResult 對象。這包括系數和擬合模型時返回的所有其他內部數據。 * _model_bias.npy_ 這是存儲為單行，單列 NumPy 數組的偏差值。 ### 7.2 進行預測一個自然的例子可能是加載模型并進行單一預測。這是相對簡單的，包括恢復保存的模型和偏差并調用 _forecast（）_ 方法。要反轉季節差異，還必須加載歷史數據。下面的示例加載模型，對下一個時間步進行預測，并打印預測。 ```py from pandas import Series from statsmodels.tsa.arima_model import ARIMAResults import numpy # invert differenced value def inverse_difference(history, yhat, interval=1): return yhat + history[-interval] series = Series.from_csv('dataset.csv') months_in_year = 12 model_fit = ARIMAResults.load('model.pkl') bias = numpy.load('model_bias.npy') yhat = float(model_fit.forecast()[0]) yhat = bias + inverse_difference(series.values, yhat, months_in_year) print('Predicted: %.3f' % yhat) ``` 運行該示例打印約 6794 的預測。 ```py Predicted: 6794.773 ``` 如果我們查看 _validation.csv_ ，我們可以看到下一個時間段第一行的值是 6981。預測是在正確的球場。 ### 7.3 驗證模型我們可以加載模型并以假裝操作方式使用它。在測試工具部分中，我們將原始數據集的最后 12 個月保存在單獨的文件中以驗證最終模型。我們現在可以加載這個 _validation.csv_ 文件并使用它看看我們的模型在“看不見的”數據上的真實程度。我們可以通過兩種方式進行： * 加載模型并使用它來預測未來 12 個月。超過前一兩個月的預測將很快開始降低技能。 * 加載模型并以滾動預測方式使用它，更新每個時間步的變換和模型。這是首選方法，因為它是如何在實踐中使用此模型，因為它將實現最佳表現。與前幾節中的模型評估一樣，我們將以滾動預測的方式進行預測。這意味著我們將在驗證數據集中逐步超過提前期，并將觀察結果作為歷史記錄的更新。 ```py from pandas import Series from matplotlib import pyplot from statsmodels.tsa.arima_model import ARIMA from statsmodels.tsa.arima_model import ARIMAResults from sklearn.metrics import mean_squared_error from math import sqrt import numpy # create a differenced series def difference(dataset, interval=1): diff = list() for i in range(interval, len(dataset)): value = dataset[i] - dataset[i - interval] diff.append(value) return diff # invert differenced value def inverse_difference(history, yhat, interval=1): return yhat + history[-interval] # load and prepare datasets dataset = Series.from_csv('dataset.csv') X = dataset.values.astype('float32') history = [x for x in X] months_in_year = 12 validation = Series.from_csv('validation.csv') y = validation.values.astype('float32') # load model model_fit = ARIMAResults.load('model.pkl') bias = numpy.load('model_bias.npy') # make first prediction predictions = list() yhat = float(model_fit.forecast()[0]) yhat = bias + inverse_difference(history, yhat, months_in_year) predictions.append(yhat) history.append(y[0]) print('>Predicted=%.3f, Expected=%3.f' % (yhat, y[0])) # rolling forecasts for i in range(1, len(y)): # difference data months_in_year = 12 diff = difference(history, months_in_year) # predict model = ARIMA(diff, order=(0,0,1)) model_fit = model.fit(trend='nc', disp=0) yhat = model_fit.forecast()[0] yhat = bias + inverse_difference(history, yhat, months_in_year) predictions.append(yhat) # observation obs = y[i] history.append(obs) print('>Predicted=%.3f, Expected=%3.f' % (yhat, obs)) # report performance mse = mean_squared_error(y, predictions) rmse = sqrt(mse) print('RMSE: %.3f' % rmse) pyplot.plot(y) pyplot.plot(predictions, color='red') pyplot.show() ``` 運行該示例將打印驗證數據集中時間步長的每個預測值和預期值。驗證期的最終 RMSE 預計為 361.110 萬銷售。這遠遠超過了每月銷售額超過 9.24 億美元的預期。 ```py >Predicted=6794.773, Expected=6981 >Predicted=10101.763, Expected=9851 >Predicted=13219.067, Expected=12670 >Predicted=3996.535, Expected=4348 >Predicted=3465.934, Expected=3564 >Predicted=4522.683, Expected=4577 >Predicted=4901.336, Expected=4788 >Predicted=5190.094, Expected=4618 >Predicted=4930.190, Expected=5312 >Predicted=4944.785, Expected=4298 >Predicted=1699.409, Expected=1413 >Predicted=6085.324, Expected=5877 RMSE: 361.110 ``` 還提供了與驗證數據集相比較的預測圖。按照這個規模，12 個月的預測銷售數據看起來很棒。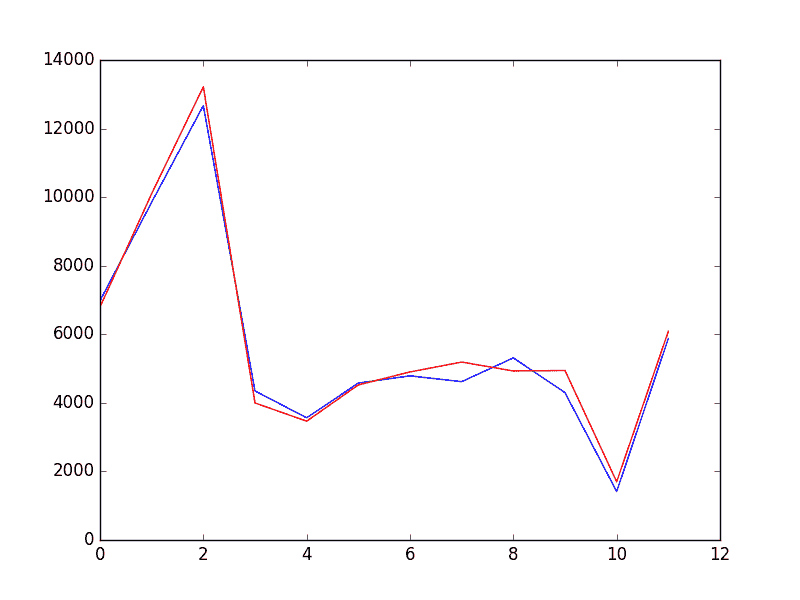 ![Forecast for Champagne Sales Validation Dataset](https://img.kancloud.cn/40/8d/408dad81234dff5fa732a5e1157848a4_800x600.jpg) 香檳銷售驗證數據集預測 ## 摘要在本教程中，您使用 Python 發現了時間序列預測項目的步驟和工具。我們在本教程中介紹了很多內容;特別： * 如何開發具有表現測量和評估方法的測試工具，以及如何快速開發基線預測和技能。 * 如何使用時間序列分析來提出如何最好地模擬預測問題的想法。 * 如何開發 ARIMA 模型，保存它，然后加載它以對新數據進行預測。你是怎么做的？您對本教程有任何疑問嗎？在下面的評論中提出您的問題，我會盡力回答。