>本文轉載至：[http://c.biancheng.net/view/1725.html](http://c.biancheng.net/view/1725.html) > 對于基礎薄弱的讀者，本節的內容可能略顯晦澀和枯燥，如果你覺得吃力，可以暫時跳過，基本不會影響后續章節的學習，等用到的時候再來閱讀。 上節我們對二進制、八進制和十六進制進行了說明，本節重點講解不同進制之間的轉換，這在編程中經常會用到，尤其是C語言。 ## 將二進制、八進制、十六進制轉換為十進制 二進制、八進制和十六進制向十進制轉換都非常容易，就是“按權相加”。所謂“權”，也即“位權”。 假設當前數字是 N 進制，那么： * 對于整數部分，從右往左看，第 i 位的位權等于Ni-1 * 對于小數部分，恰好相反，要從左往右看，第 j 位的位權為N\-j。 更加通俗的理解是，假設一個多位數（由多個數字組成的數）某位上的數字是 1，那么它所表示的數值大小就是該位的位權。 #### 1) 整數部分 例如，將八進制數字?53627 轉換成十進制： 53627 =?5×84?+ 3×83?+ 6×82?+ 2×81?+ 7×80?=?22423（十進制） 從右往左看，第1位的位權為 80\=1，第2位的位權為 81\=8，第3位的位權為 82\=64，第4位的位權為 83\=512，第5位的位權為 84\=4096 …… 第n位的位權就為 8n-1。將各個位的數字乘以位權，然后再相加，就得到了十進制形式。 > 注意，這里我們需要以十進制形式來表示位權。 再如，將十六進制數字 9FA8C 轉換成十進制： 9FA8C =?9×164?+ 15×163?+ 10×162?+ 8×161?+ 12×160?=?653964（十進制） 從右往左看，第1位的位權為 160\=1，第2位的位權為 161\=16，第3位的位權為 162\=256，第4位的位權為 163\=4096，第5位的位權為 164\=65536 …… 第n位的位權就為 16n-1。將各個位的數字乘以位權，然后再相加，就得到了十進制形式。 將二進制數字轉換成十進制也是類似的道理： 11010 = 1×24?+ 1×23?+ 0×22?+ 1×21?+ 0×20?= 26（十進制） 從右往左看，第1位的位權為 20\=1，第2位的位權為 21\=2，第3位的位權為 22\=4，第4位的位權為 23\=8，第5位的位權為 24\=16 …… 第n位的位權就為 2n-1。將各個位的數字乘以位權，然后再相加，就得到了十進制形式。 #### 2) 小數部分 例如，將八進制數字 423.5176 轉換成十進制： 423.5176?=?4×82?+ 2×81?+ 3×80?+ 5×8\-1?+ 1×8\-2?+ 7×8\-3?+ 6×8\-4?=?275.65576171875（十進制） 小數部分和整數部分相反，要從左往右看，第1位的位權為 8\-1\=1/8，第2位的位權為 8\-2\=1/64，第3位的位權為 8\-3\=1/512，第4位的位權為 8\-4\=1/4096?…… 第m位的位權就為 8\-m。 再如，將二進制數字 1010.1101 轉換成十進制： 1010.1101 = 1×23?+ 0×22?+ 1×21?+ 0×20?+ 1×2\-1?+ 1×2\-2?+ 0×2\-3?+ 1×2\-4?=?10.8125（十進制） 小數部分和整數部分相反，要從左往右看，第1位的位權為 2\-1\=1/2，第2位的位權為 2\-2\=1/4，第3位的位權為 2\-3\=1/8，第4位的位權為 2\-4\=1/16?…… 第m位的位權就為 2\-m。 更多轉換成十進制的例子： * 二進制：1001 = 1×23?+ 0×22?+ 0×21?+ 1×20?= 8 + 0 + 0 + 1 = 9（十進制） * 二進制：101.1001 = 1×22?+ 0×21?+ 1×20?+?1×2\-1?+ 0×2\-2?+ 0×2\-3?+ 1×2\-4?= 4 + 0 + 1 + 0.5 + 0 + 0 + 0.0625 = 5.5625（十進制） * 八進制：302 = 3×82?+ 0×81?+ 2×80?= 192 + 0 + 2 = 194（十進制） * 八進制：302.46 = 3×82?+ 0×81?+ 2×80?+ 4×8\-1?+ 6×8\-2?= 192 + 0 + 2 + 0.5 + 0.09375= 194.59375（十進制） * 十六進制：EA7 = 14×162?+ 10×161?+ 7×160?=?3751（十進制） ## 將十進制轉換為二進制、八進制、十六進制 將十進制轉換為其它進制時比較復雜，整數部分和小數部分的算法不一樣，下面我們分別講解。 #### 1) 整數部分 十進制整數轉換為 N 進制整數采用“除 N 取余，逆序排列”法。具體做法是： * 將 N 作為除數，用十進制整數除以 N，可以得到一個商和余數； * 保留余數，用商繼續除以 N，又得到一個新的商和余數； * 仍然保留余數，用商繼續除以 N，還會得到一個新的商和余數； * …… * 如此反復進行，每次都保留余數，用商接著除以 N，直到商為 0 時為止。 把先得到的余數作為 N 進制數的低位數字，后得到的余數作為 N 進制數的高位數字，依次排列起來，就得到了 N 進制數字。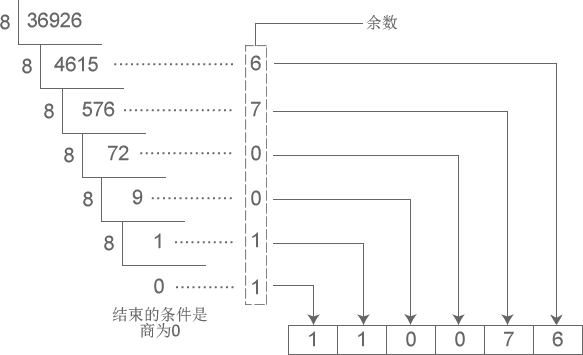 下圖演示了將十進制數字 36926 轉換成八進制的過程：  從圖中得知，十進制數字 36926 轉換成八進制的結果為 110076。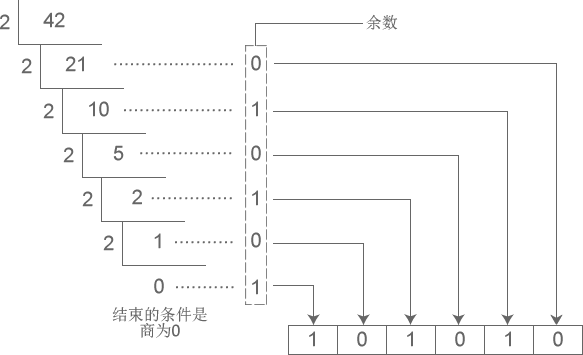 下圖演示了將十進制數字 42 轉換成二進制的過程：  從圖中得知，十進制數字 42 轉換成二進制的結果為 101010。 #### 2) 小數部分 十進制小數轉換成 N 進制小數采用“乘 N 取整，順序排列”法。具體做法是： * 用 N 乘以十進制小數，可以得到一個積，這個積包含了整數部分和小數部分； * 將積的整數部分取出，再用 N 乘以余下的小數部分，又得到一個新的積； * 再將積的整數部分取出，繼續用 N 乘以余下的小數部分； * …… * 如此反復進行，每次都取出整數部分，用 N 接著乘以小數部分，直到積中的小數部分為 0，或者達到所要求的精度為止。 把取出的整數部分按順序排列起來，先取出的整數作為 N 進制小數的高位數字，后取出的整數作為低位數字，這樣就得到了 N 進制小數。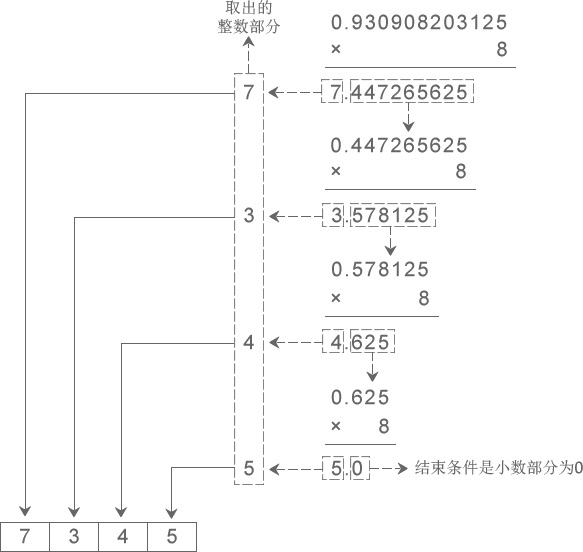 下圖演示了將十進制小數 0.930908203125 轉換成八進制小數的過程：  從圖中得知，十進制小數 0.930908203125 轉換成八進制小數的結果為 0.7345。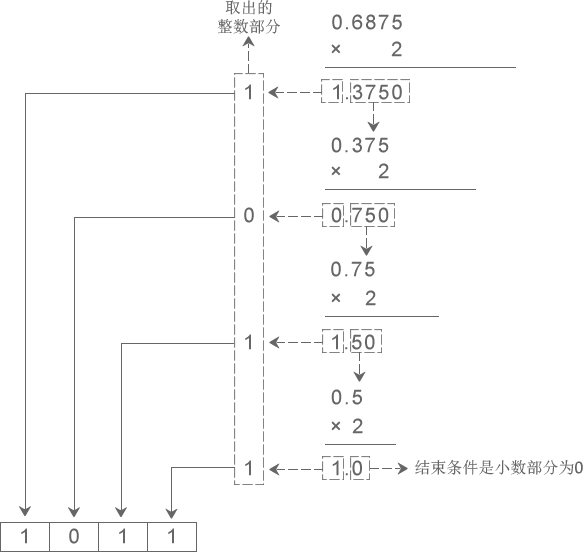 下圖演示了將十進制小數 0.6875 轉換成二進制小數的過程：  從圖中得知，十進制小數 0.6875?轉換成二進制小數的結果為 0.1011。 如果一個數字既包含了整數部分又包含了小數部分，那么將整數部分和小數部分開，分別按照上面的方法完成轉換，然后再合并在一起即可。例如： * 十進制數字 36926.930908203125 轉換成八進制的結果為?110076.7345； * 十進制數字 42.6875 轉換成二進制的結果為?101010.1011。 下表列出了前 17 個十進制整數與二進制、八進制、十六進制的對應關系： 十進制012345678910111213141516二進制0110111001011101111000100110101011110011011110111110000八進制01234567101112131415161720十六進制0123456789ABCDEF10 注意，十進制小數轉換成其他進制小數時，結果有可能是一個無限位的小數。請看下面的例子： * 十進制 0.51 對應的二進制為?0.100000101000111101011100001010001111010111...，是一個循環小數； * 十進制 0.72 對應的二進制為 0.1011100001010001111010111000010100011110...，是一個循環小數； * 十進制 0.625 對應的二進制為 0.101，是一個有限小數。 ## 二進制和八進制、十六進制的轉換 其實，任何進制之間的轉換都可以使用上面講到的方法，只不過有時比較麻煩，所以一般針對不同的進制采取不同的方法。將二進制轉換為八進制和十六進制時就有非常簡潔的方法，反之亦然。 #### 1) 二進制整數和八進制整數之間的轉換 二進制整數轉換為八進制整數時，每三位二進制數字轉換為一位八進制數字，運算的順序是從低位向高位依次進行，高位不足三位用零補齊。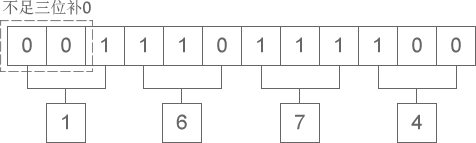下圖演示了如何將二進制整數 1110111100 轉換為八進制：  從圖中可以看出，二進制整數 1110111100 轉換為八進制的結果為 1674。 八進制整數轉換為二進制整數時，思路是相反的，每一位八進制數字轉換為三位二進制數字，運算的順序也是從低位向高位依次進行。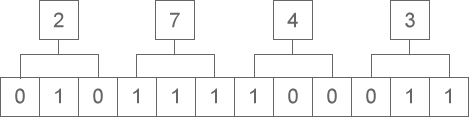下圖演示了如何將八進制整數 2743 轉換為二進制：  從圖中可以看出，八進制整數 2743 轉換為二進制的結果為 10111100011。 #### 2) 二進制整數和十六進制整數之間的轉換 二進制整數轉換為十六進制整數時，每四位二進制數字轉換為一位十六進制數字，運算的順序是從低位向高位依次進行，高位不足四位用零補齊。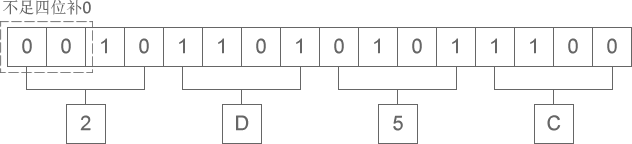下圖演示了如何將二進制整數 10 1101 0101 1100?轉換為十六進制：  從圖中可以看出，二進制整數 10 1101 0101 1100 轉換為十六進制的結果為 2D5C。 十六進制整數轉換為二進制整數時，思路是相反的，每一位十六進制數字轉換為四位二進制數字，運算的順序也是從低位向高位依次進行。下圖演示了如何將十六進制整數 A5D6 轉換為二進制：  從圖中可以看出，十六進制整數 A5D6 轉換為二進制的結果為 1010 0101 1101 0110。