# [跳表(SkipList)原理篇] # 1、什么是跳表？ 維基百科：跳表是一種數據結構。它使得包含n個元素的有序序列的查找和插入操作的平均時間復雜度都是 O(logn)，優于數組的 O(n)復雜度。快速的查詢效果是通過維護一個多層次的鏈表實現的，且與前一層（下面一層）鏈表元素的數量相比，每一層鏈表中的元素的數量更少。 * 優于數組的插入操作時間復雜度 簡單理解跳表是基于鏈表實現的有序列表，跳表通過維護一個多層級的鏈表實現了快速查詢效果將平均時間復雜度降到了O($log^n$)，這是一個典型的異空間換時間數據結構。 # 2、為什么需要跳表？ 在實際開發中經常遇到需要在數據集中查找一個指定數據的場景，而常用的支持高效查找算法的實現方式有以下幾種： 1. 有序數組。插入時可以先對數據排序，查詢時可以采用二分查找算法降低查找操作的復雜度。缺點是插入和刪除數據時，為了保持元素的有序性，需要進行大量數據的移動操作。 2. 二叉查找樹。既支持高效的二分查找算法，又能快速的進行插入和刪除操作的數據結構,理想的時間復雜度為 O($log^n$)，但是在某些極端情況下，二叉查找樹有可能變成一個線性鏈表，即退化成鏈表結構。 3. 平衡二叉樹。基于二叉查找樹的優點，對其缺點進行了優化改進，引入了平衡的概念。為了維持二叉樹的平衡衍生出了多種平衡算法，根據平衡算法的不同具體實現有AVL樹 /B樹（B-Tree）/ B+樹（B+Tree）／紅黑樹 等等。但是平衡算法的實現大多數比較復雜且較難理解。 針對大體量、海量數據集中查找指定數據有更好的解決方案，我們得評估時間、空間的成本和收益。 跳表同樣支持對數據進行高效的查找，插入和刪除數據操作時間復雜度能與平衡二叉樹媲美，最重要的是跳表的實現比平衡二叉樹簡單幾個級別。缺點就是“以空間換時間”方式存在一定數據冗余。 如果存儲的數據是大對象，跳表冗余的只是指向數據的指針，幾乎可以不計使用的內存空間。 # 3、跳表的實現原理 添加、刪除操作都需要先查詢出操作數據的位置，所以理解了跳表的查詢原理后，剩下的只是對鏈表的操作。 ## 3.1、查詢數據 例設原始鏈表上的有序數據為【9,11,14,19,20,24,27】，如果我要查找的數據是20，只能從頭結點沿著鏈表依次比較查找，如圖所示：  鏈表不能像數組那樣通過索引快速訪問數據，只能沿著指針方向依次訪問，所以不能使用二分查找算法快速進行數據查詢。但是可以借鑒創建索引的這種思路，就像圖書的目錄一樣，如果我要查看第六章的內容，直接翻到通過目錄查詢到的第六章對應頁碼處就行。 這里的目錄就相當于創建的索引，該索引能夠縮小我們查詢數據的范圍減少查詢次數。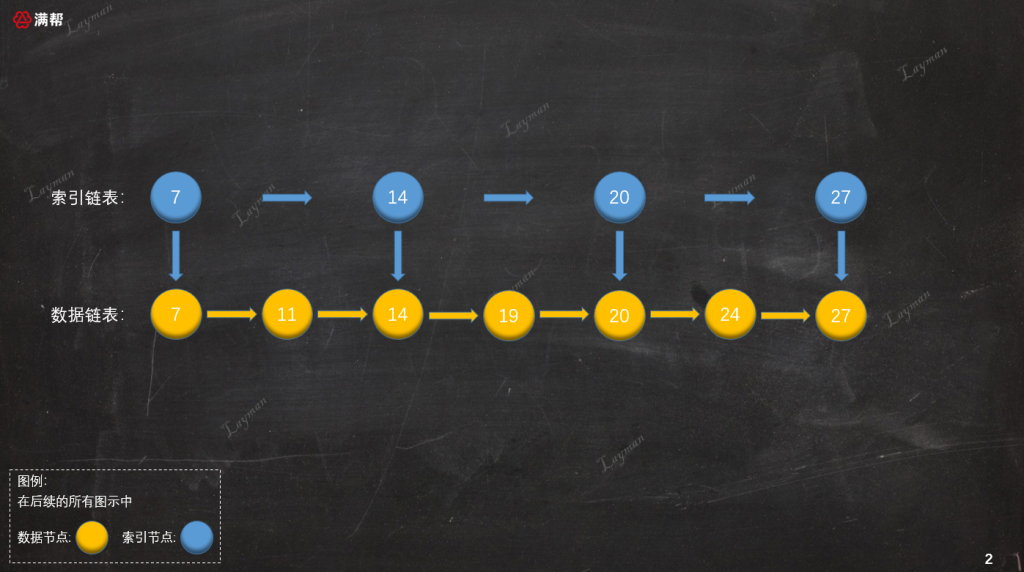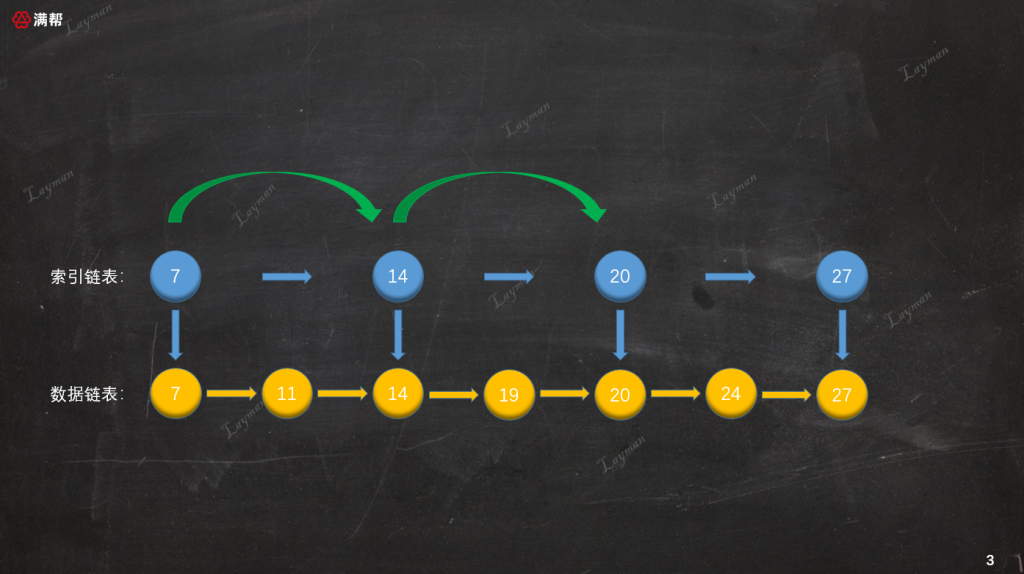在原始鏈表的基礎上，我們增加一層索引鏈表，假如原始鏈表的每兩個結點就有一個結點也在索引鏈表當中，如圖所示：  當建立了索引后檢索數據的方式就發生了變化，當我們想要定位到`DataNode-20`，我們不需要在原始鏈表中一個一個結點訪問，而是首先訪問索引鏈表：  由于索引鏈表的結點個數是原始鏈表的一半，查找結點所需的訪問次數也就相應減少了一半，經過兩次查詢我們便找到`DataNode-20`。 正如圖書的目錄不止按照“章節”劃分，還可以按照“第幾部分”、“第幾小節”進行劃分，鏈表的索引也一樣。我們可以繼續為鏈表創建更多層索引，每層索引節點為前一層索引(對應圖例的下一層)的一半，在數據量比較大時能夠大大的提升我們的查詢效率。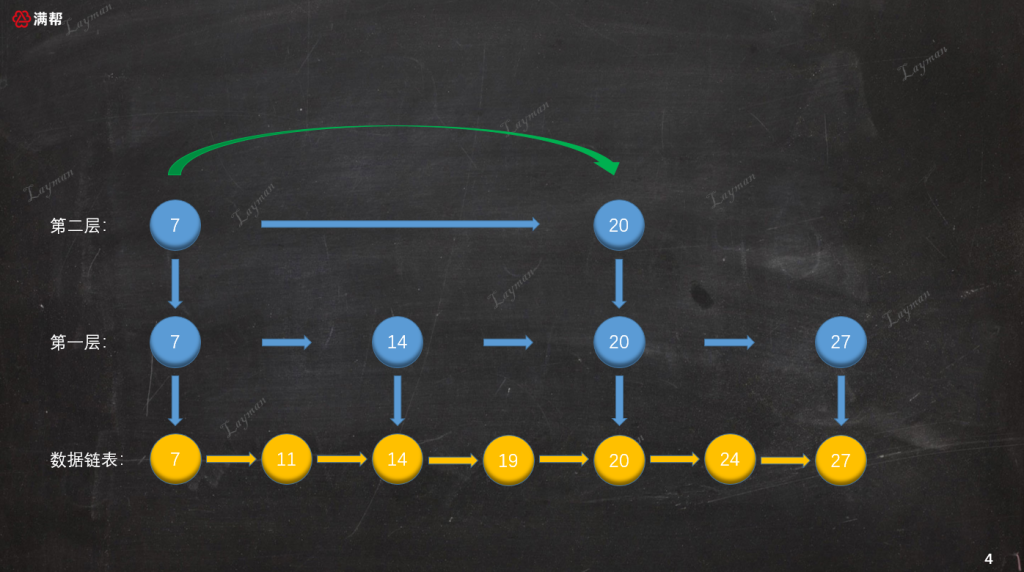  如圖所示，我們基于原始鏈表的第1層索引，抽出了第2層更為稀疏的索引，結點數量是第1層索引的一半。這樣的多層索引可以進一步提升查詢效率，那么它是如何進行查詢的呢？假如這次要查找`DataNode-27`，讓我們來演示一下檢索過程： 1. 首先，我們從最上層(第二層)的`HeadIndex-7`開始查找，`HeadIndex-7`指向`DataNode-7`比`DataNode-27`小，所以繼續向右查詢找到第二個索引節點`IndexNode-20`。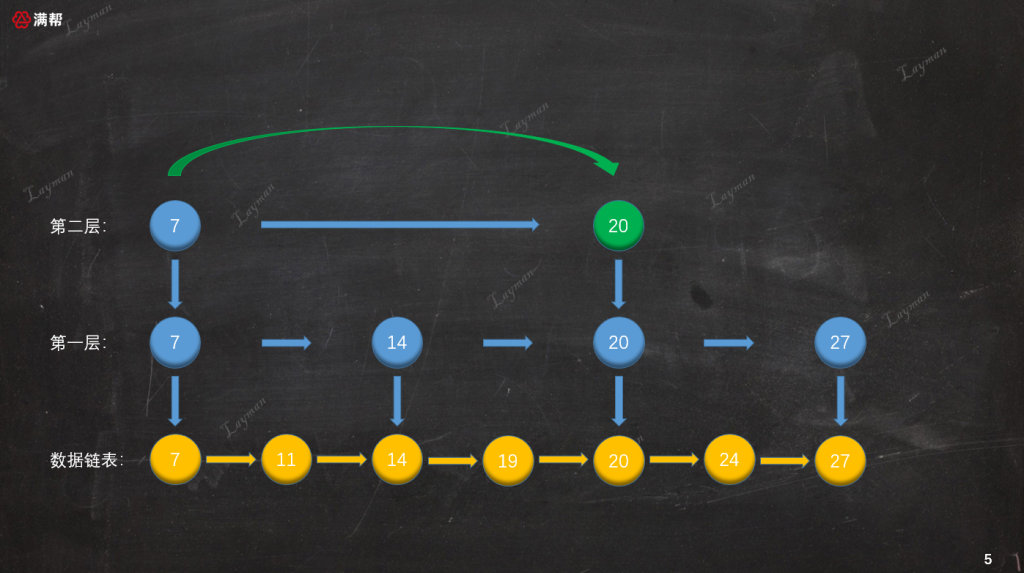  2. `IndexNode-20`指向`DataNode-20`也比`DataNode-27`小，但是此時第二層已經沒有后續的索引節點，所以我們需要順著`IndexNode-20`訪問下一層索引，即第一層的`IndexNode-20`。 從索引節點訪問方式可知，索引節點保存著“數據節點”、“下層索引節點”的指針。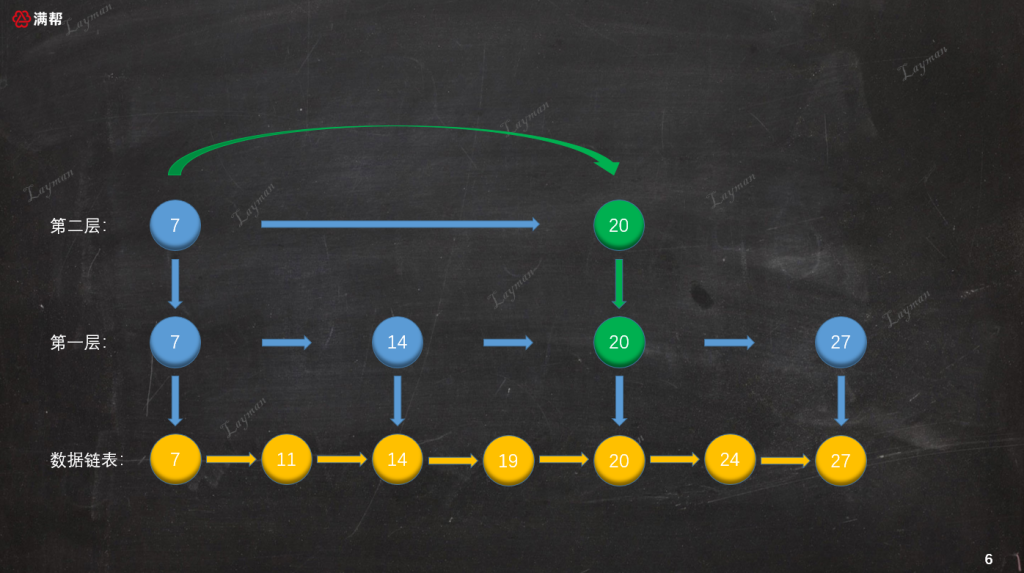  3. 通過第一層的`IndexNode-20`繼續向右檢索找到`IndexNode-27`便檢索到了`DataNode-27`。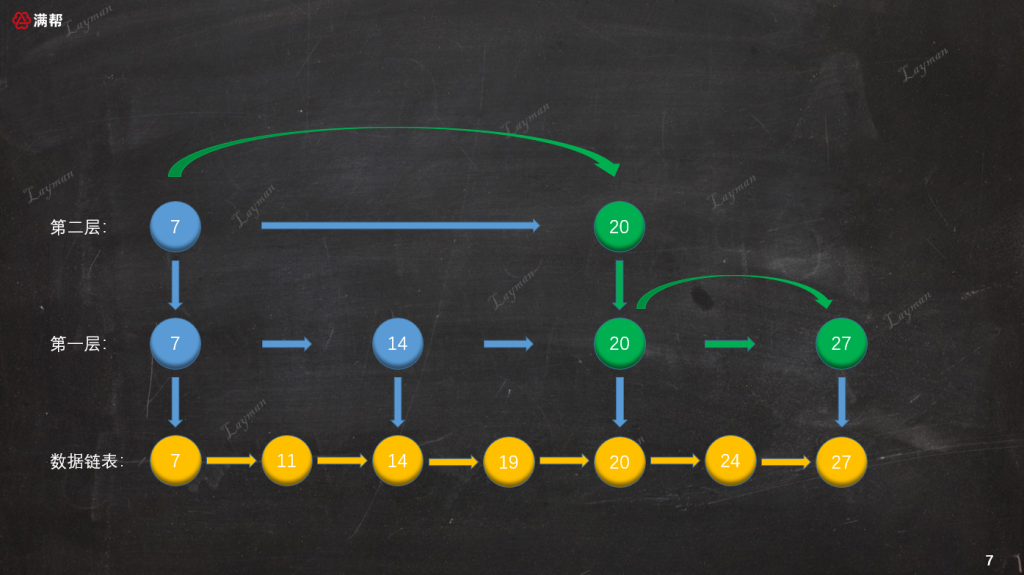  總結： 維基百科： 跳躍列表是按層建造的。底層是一個普通的有序鏈表。每個更高層都充當下面列表的“快速通道”，這里在第 i 層中的元素按某個固定的概率 $p$（通常為 $\\frac 12$ 或 $\\frac 14$ 出現在第 i + 1 層中。每個元素平均出現在 ${1\\over 1-p}$ 個列表中，而最高層的元素（通常是在跳躍列表前端的一個特殊的頭元素）在 $log\_{1/p}^n$個列表中出現。 在查找目標元素時，從頂層列表、頭元素起步。算法沿著每層鏈表搜索，直至找到一個大于或等于目標的元素，或者到達當前層列表末尾。如果該元素等于目標元素，則表明該元素已被找到；如果該元素大于目標元素或已到達鏈表末尾，則退回到當前層的上一個元素，然后轉入下一層進行搜索。每層鏈表中預期的查找步數最多為$\\frac 1p$，而層數為 -${log\_p^n}\\over{p}$，由于 $p$ 是常數，查找操作總體的時間復雜度為 O($log^n$)。而通過選擇不同 $p$ 值，就可以在查找代價和存儲代價之間獲取平衡。 上面的查詢例子中索引節點已經是創建好的，那么原始鏈表哪些數據節點需要創建索引節點、什么時候創建？這些問題的答案都要回歸到往原始鏈表添加數據時。 ## 3.2、插入數據 從上面的總結不難理解在向原始鏈表中插入數據時，當前插入的數據按照某個固定的概率$p$($\\frac 12$ 或 $\\frac 14$)在每層索引鏈表中創建索引節點。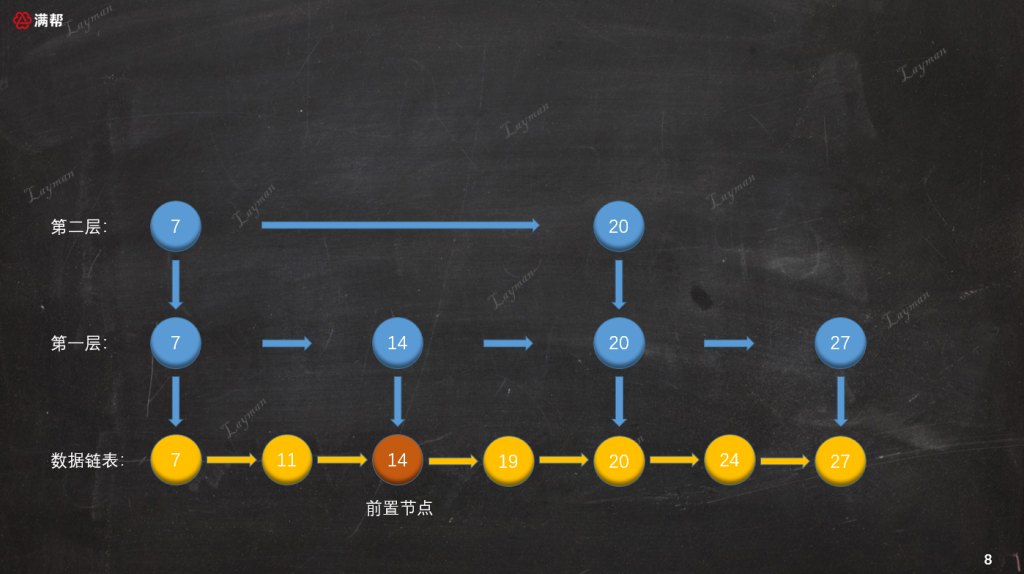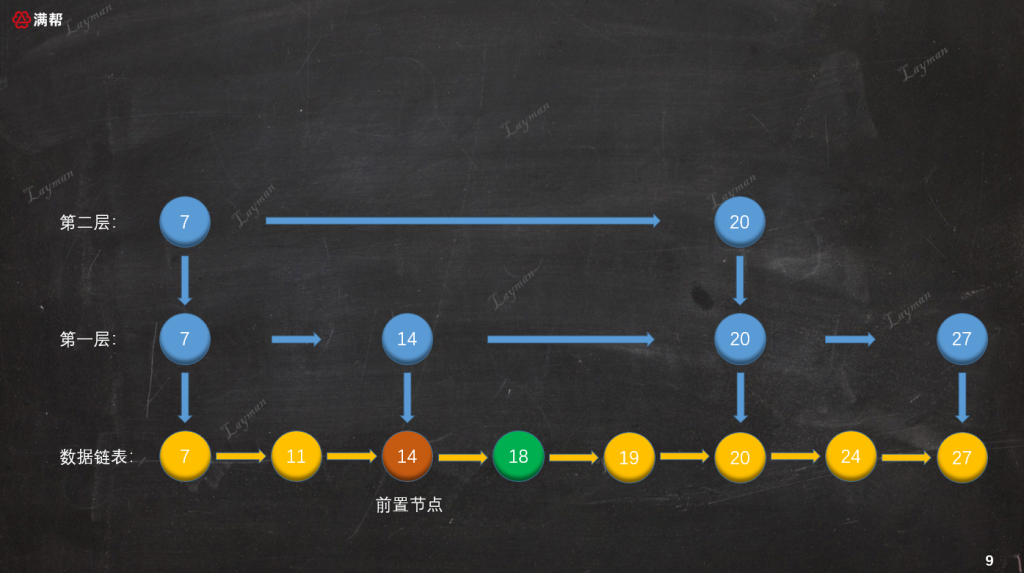假設現在插入`DataNode-18`，我們來看看是如何插入和創建索引節點的： ### 3.2.1、找到插入數據的前置節點 首先我們按照跳表查找結點的方法，找到待插入結點的前置結點（僅小于待插入結點）:  ### 3.2.2、插入原始鏈表 接下來按照一般鏈表的插入方式，把`DataNode-18`插入到結點`DataNode-14`的后續位置：  這樣數據就插入到了原始鏈表中，但是我們的插入操作并沒有結束。按照定義我們需要讓新插入的結點隨機(拋硬幣的方式)“晉升”，也就是為`DataNode-18`創建索引節點，正是采取這種簡單的隨機方式,跳表也被稱為一種隨機化的數據結構。 ### 3.2.3、創建索引節點 假設第一、第二次隨機的結果都是晉升成功，那么我們需要為`DataNode-18`創建索引節點，插入到第一層和第二層索引的對應位置，并且向下指向原始鏈表的`DataNode-18`。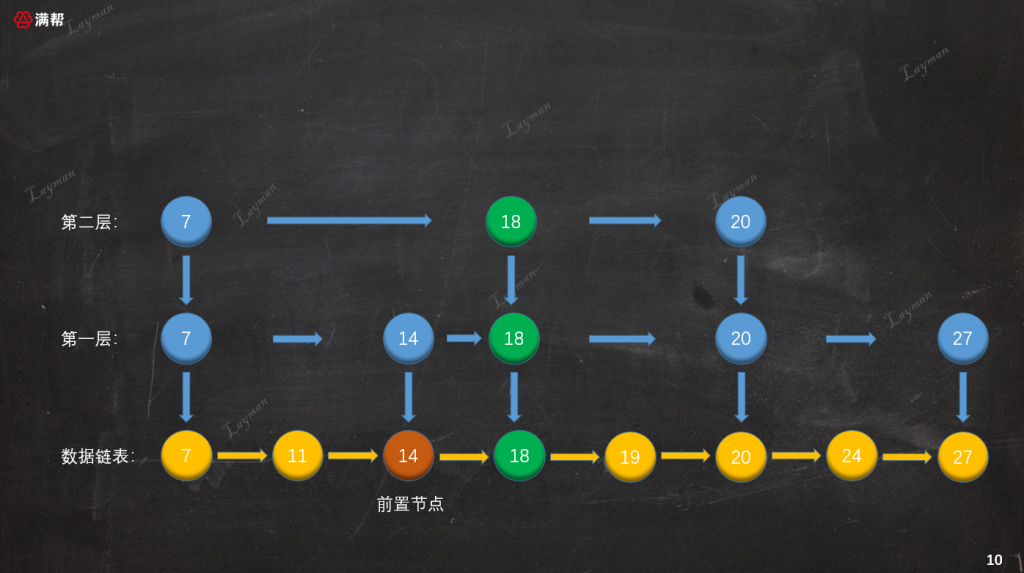  在索引鏈表中插入新創建的索引節點時需要注意幾點： 1. 找到待插入索引節點的前置索引節點指向新索引節點，新索引節點指向前置節點之前指向的索引節點。（也就是鏈表的插入操作） 2. 隨機的結果是“晉升成功”就可以繼續向上一層創建索引，直到假設隨機的結果是“晉升失敗”或者“新增索引層”。 3. 每層是否創建索引節點可以一次性拋幾次硬幣，而不是添加一層索引后再進行投幣。(這樣做的目的是為了更好的用代碼實現)。 新建的索引節點何如銜接到前置索引節點以及如何用代碼實現，這個我們在下篇文章“SkipList 代碼實現”去解析。 ### 3.2.4、添加索引層 如果在第二層(目前索引最大層級)創建索引節點后，下一次隨機的結果仍然是晉升成功，這時候該怎么辦呢？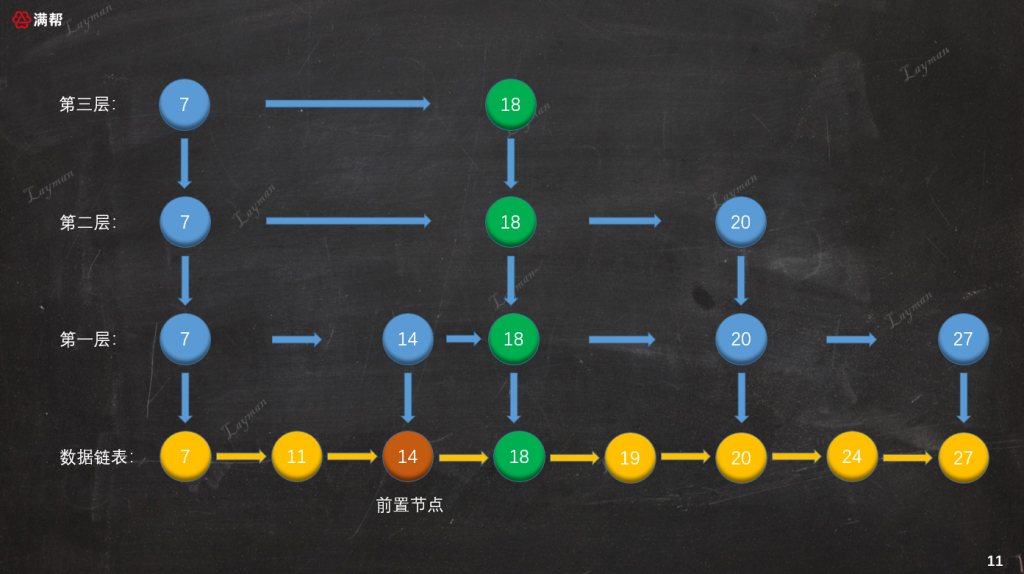這個時候我們就需要添加一層索引層：  可以看到此時第三層只有`HeadIndex-7`和`IndexNode-18`，此時不會繼續向上層創建索引，因為就算繼續創建仍只有`HeadIndex-7`和`IndexNode-18`，這顯得毫無意義。至此跳表的插入操作包括索引的創建過程已經解析完，跳表的刪除過程正好和插入是相反的思路。 ## 3.3、刪除數據 ### 3.3.1、查找待刪除節點 假設我們要刪除剛才插入的`DataNode-18`，首先我們要按照跳表查找結點的方法找到待刪除的`DataNode-18`，當然如果沒有找到對應的數據直接返回進行。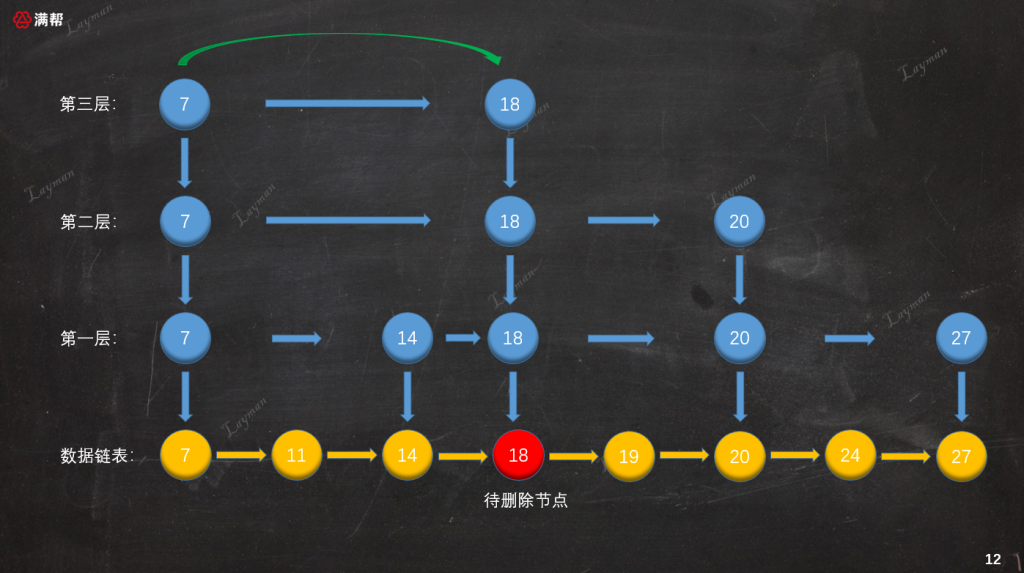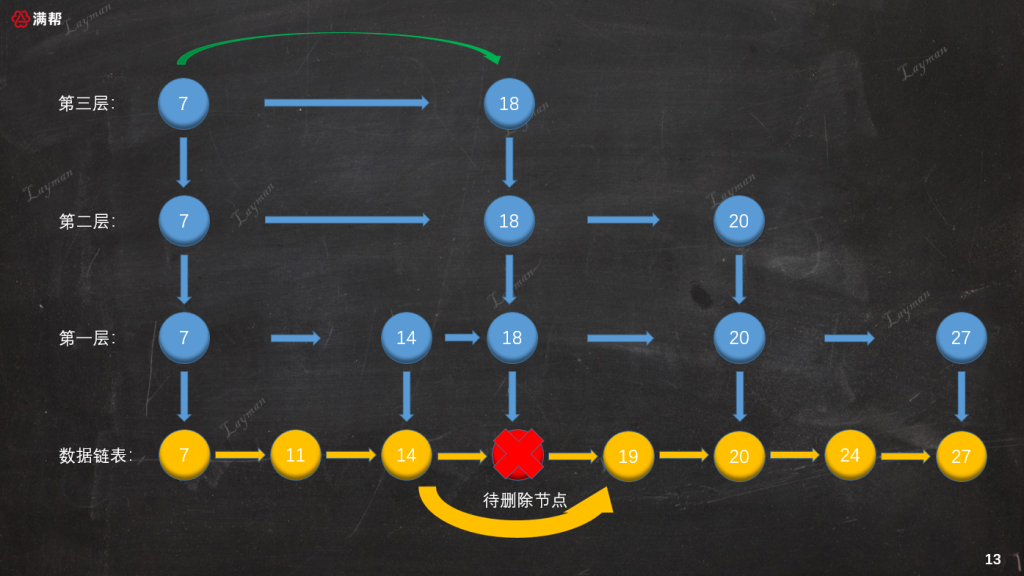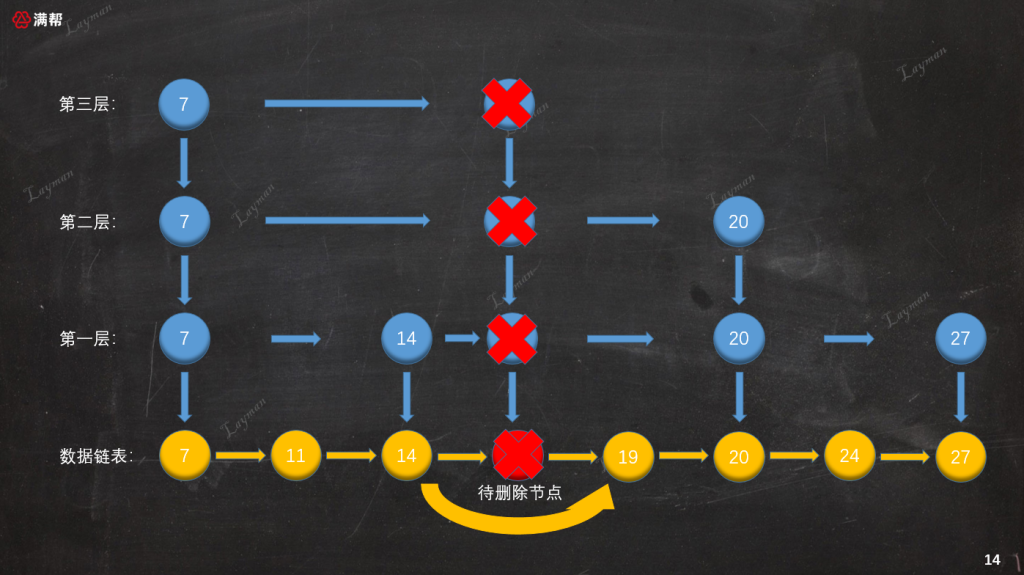  ### 3.3.2、刪除原始鏈表節點 接下來按照鏈表的刪除方式，把`DataNode-18`從原始鏈表當中刪除  ### 3.3.3、刪除索引節點 同插入數據一樣，刪除工作并沒有就此完成，我們需要將`DataNode-18`在索引層對應的`IndexNode-18`也一 一刪除：  ### 3.3.4、刪除索引層 同插入索引節點一樣，刪除索引節點時也需要維護前置節點的指向關系。這里需要特別注意最上層索引(第三層)，當刪除`IndexNode-18`后該層只剩下`HeadIndex-7`，這個時候需要將該索引層也一同刪除。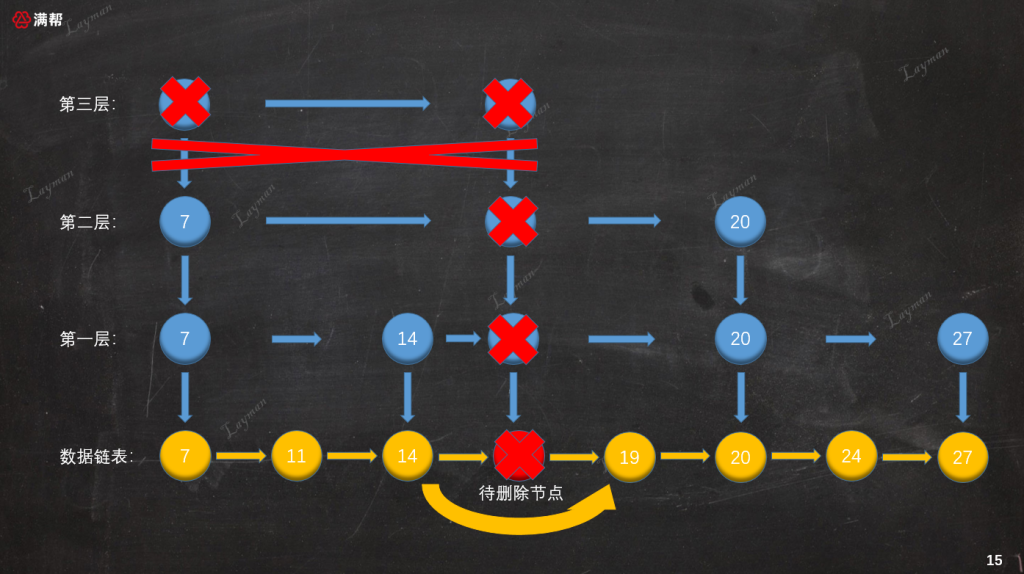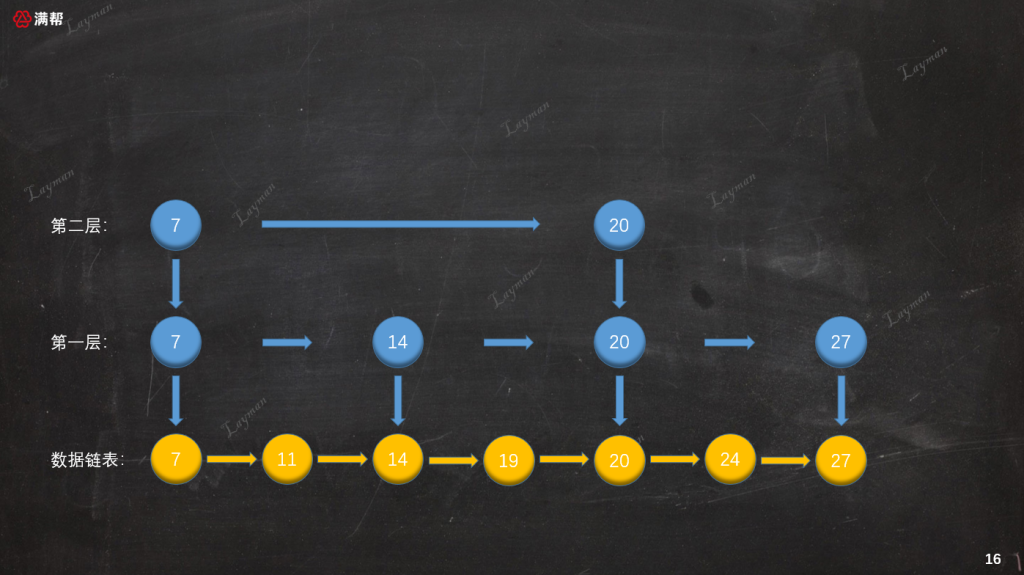  至此整個刪除操作就算完成了，此時跳表的結構就和我們之前插入之前保持一致了：  總結 1. 簡單對比了跳表和其他幾種高效查找算法的優缺點。 2. 跳表是基于鏈表實現的，是一種“以空間換時間”的“隨機化”數據結構。 3. 跳表引入了索引層的概念，有了它才有了時間復雜度為O($logn$)的查詢效率,從而實現了增刪操作的時間復雜度也是O($logn$)。 4. 跳表擁有平衡二叉樹相同的查詢效率，但是跳表對于樹平衡的實現是基于一種隨機化的算法的，相對于AVL樹/B樹（B-Tree）/B+樹（B+Tree）/紅黑樹的實現簡單得多。 Java實現跳表的代碼示例 ``` import java.util.Random; // 定義跳表節點類 class SkipListNode { int value; // 節點的值 SkipListNode[] forward; // 指向下一層的指針數組 // 構造函數，初始化節點 public SkipListNode(int level, int value) { this.value = value; this.forward = new SkipListNode[level + 1]; // 初始化指針數組 } } // 定義跳表類 public class SkipList { private static final int MAX_LEVEL = 16; // 跳表的最大層數 private final SkipListNode head; // 頭節點 private int level; // 當前跳表的層數 private final Random random; // 隨機數生成器 // 構造函數，初始化跳表 public SkipList() { head = new SkipListNode(MAX_LEVEL, Integer.MIN_VALUE); // 初始化頭節點 level = 0; // 初始層數為0 random = new Random(); // 初始化隨機數生成器 } // 插入操作 public void insert(int value) { SkipListNode[] update = new SkipListNode[MAX_LEVEL + 1]; // 用于存儲每層需要更新的節點 SkipListNode current = head; // 從頭節點開始 // 從最高層向下查找插入位置 for (int i = level; i >= 0; i--) { while (current.forward[i] != null && current.forward[i].value < value) { current = current.forward[i]; } update[i] = current; // 記錄需要更新的節點 } int newLevel = randomLevel(); // 隨機生成新節點的層數 if (newLevel > level) { // 如果新節點的層數大于當前層數，更新當前層數 for (int i = level + 1; i <= newLevel; i++) { update[i] = head; } level = newLevel; } // 創建新節點，并插入到每一層的鏈表中 SkipListNode newNode = new SkipListNode(newLevel, value); for (int i = 0; i <= newLevel; i++) { newNode.forward[i] = update[i].forward[i]; update[i].forward[i] = newNode; } } // 查找操作 public boolean search(int value) { SkipListNode current = head; // 從頭節點開始 // 從最高層向下查找目標值 for (int i = level; i >= 0; i--) { // 每層逐個節點比較 while (current.forward[i] != null && current.forward[i].value < value) { current = current.forward[i]; } } current = current.forward[0]; // 到達底層鏈表 return current != null && current.value == value; // 判斷是否找到目標值 } // 隨機生成節點的層數 private int randomLevel() { int lvl = 0; while (random.nextInt(2) == 1 && lvl < MAX_LEVEL) { lvl++; } return lvl; } // 主函數，測試跳表的插入和查找操作 public static void main(String[] args) { SkipList skipList = new SkipList(); skipList.insert(3); skipList.insert(6); skipList.insert(7); skipList.insert(9); skipList.insert(12); skipList.insert(19); System.out.println(skipList.search(9)); // 輸出 true，表示找到目標值9 System.out.println(skipList.search(15)); // 輸出 false，表示沒有找到目標值15 } } ```