### 一 斐波那契數列 #### **題目描述：** 大家都知道斐波那契數列，現在要求輸入一個整數n，請你輸出斐波那契數列的第n項。 n<=39 #### **問題分析：** 可以肯定的是這一題通過遞歸的方式是肯定能做出來，但是這樣會有一個很大的問題，那就是遞歸大量的重復計算會導致內存溢出。另外可以使用迭代法，用fn1和fn2保存計算過程中的結果，并復用起來。下面我會把兩個方法示例代碼都給出來并給出兩個方法的運行時間對比。 #### **示例代碼：** **采用迭代法：** ```java int Fibonacci(int number) { if (number <= 0) { return 0; } if (number == 1 || number == 2) { return 1; } int first = 1, second = 1, third = 0; for (int i = 3; i <= number; i++) { third = first + second; first = second; second = third; } return third; } ``` **采用遞歸：** ```java public int Fibonacci(int n) { if (n <= 0) { return 0; } if (n == 1||n==2) { return 1; } return Fibonacci(n - 2) + Fibonacci(n - 1); } ``` ### 二 跳臺階問題 #### **題目描述：** 一只青蛙一次可以跳上1級臺階，也可以跳上2級。求該青蛙跳上一個n級的臺階總共有多少種跳法。 #### **問題分析：** **正常分析法：** a.如果兩種跳法，1階或者2階，那么假定第一次跳的是一階，那么剩下的是n-1個臺階，跳法是f(n-1); b.假定第一次跳的是2階，那么剩下的是n-2個臺階，跳法是f(n-2) c.由a，b假設可以得出總跳法為: f(n) = f(n-1) + f(n-2) d.然后通過實際的情況可以得出：只有一階的時候 f(1) = 1 ,只有兩階的時候可以有 f(2) = 2 **找規律分析法：** f(1) = 1, f(2) = 2, f(3) = 3, f(4) = 5， 可以總結出f(n) = f(n-1) + f(n-2)的規律。 但是為什么會出現這樣的規律呢？假設現在6個臺階，我們可以從第5跳一步到6，這樣的話有多少種方案跳到5就有多少種方案跳到6，另外我們也可以從4跳兩步跳到6，跳到4有多少種方案的話，就有多少種方案跳到6，其他的不能從3跳到6什么的啦，所以最后就是f(6) = f(5) + f(4)；這樣子也很好理解變態跳臺階的問題了。 **所以這道題其實就是斐波那契數列的問題。** 代碼只需要在上一題的代碼稍做修改即可。和上一題唯一不同的就是這一題的初始元素變為 1 2 3 5 8.....而上一題為1 1 2 3 5 .......。另外這一題也可以用遞歸做，但是遞歸效率太低，所以我這里只給出了迭代方式的代碼。 #### **示例代碼：** ```java int jumpFloor(int number) { if (number <= 0) { return 0; } if (number == 1) { return 1; } if (number == 2) { return 2; } int first = 1, second = 2, third = 0; for (int i = 3; i <= number; i++) { third = first + second; first = second; second = third; } return third; } ``` ### 三 變態跳臺階問題 #### **題目描述：** 一只青蛙一次可以跳上1級臺階，也可以跳上2級……它也可以跳上n級。求該青蛙跳上一個n級的臺階總共有多少種跳法。 #### **問題分析：** 假設n>=2，第一步有n種跳法：跳1級、跳2級、到跳n級 跳1級，剩下n-1級，則剩下跳法是f(n-1) 跳2級，剩下n-2級，則剩下跳法是f(n-2) ...... 跳n-1級，剩下1級，則剩下跳法是f(1) 跳n級，剩下0級，則剩下跳法是f(0) 所以在n>=2的情況下： f(n)=f(n-1)+f(n-2)+...+f(1) 因為f(n-1)=f(n-2)+f(n-3)+...+f(1) 所以f(n)=2*f(n-1) 又f(1)=1,所以可得**f(n)=2^(number-1)** #### **示例代碼：** ```java int JumpFloorII(int number) { return 1 << --number;//2^(number-1)用位移操作進行，更快 } ``` #### **補充：** **java中有三種移位運算符：** 1. “<<” : **左移運算符**，等同于乘2的n次方 2. “>>”: **右移運算符**，等同于除2的n次方 3. “>>>” **無符號右移運算符**，不管移動前最高位是0還是1，右移后左側產生的空位部分都以0來填充。與>>類似。 例： int a = 16; int b = a << 2;//左移2，等同于16 * 2的2次方，也就是16 * 4 int c = a >> 2;//右移2，等同于16 / 2的2次方，也就是16 / 4 ### 四 二維數組查找 #### **題目描述：** 在一個二維數組中，每一行都按照從左到右遞增的順序排序，每一列都按照從上到下遞增的順序排序。請完成一個函數，輸入這樣的一個二維數組和一個整數，判斷數組中是否含有該整數。 #### **問題解析：** 這一道題還是比較簡單的，我們需要考慮的是如何做，效率最快。這里有一種很好理解的思路： > 矩陣是有序的，從左下角來看，向上數字遞減，向右數字遞增， > 因此從左下角開始查找，當要查找數字比左下角數字大時。右移 > 要查找數字比左下角數字小時，上移。這樣找的速度最快。 #### **示例代碼：** ```java public boolean Find(int target, int [][] array) { //基本思路從左下角開始找，這樣速度最快 int row = array.length-1;//行 int column = 0;//列 //當行數大于0，當前列數小于總列數時循環條件成立 while((row >= 0)&& (column< array[0].length)){ if(array[row][column] > target){ row--; }else if(array[row][column] < target){ column++; }else{ return true; } } return false; } ``` ### 五 替換空格 #### **題目描述：** 請實現一個函數，將一個字符串中的空格替換成“%20”。例如，當字符串為We Are Happy.則經過替換之后的字符串為We%20Are%20Happy。 #### **問題分析：** 這道題不難，我們可以通過循環判斷字符串的字符是否為空格，是的話就利用append()方法添加追加“%20”，否則還是追加原字符。 或者最簡單的方法就是利用： replaceAll(String regex,String replacement)方法了，一行代碼就可以解決。 #### **示例代碼：** **常規做法：** ```java public String replaceSpace(StringBuffer str) { StringBuffer out=new StringBuffer(); for (int i = 0; i < str.toString().length(); i++) { char b=str.charAt(i); if(String.valueOf(b).equals(" ")){ out.append("%20"); }else{ out.append(b); } } return out.toString(); } ``` **一行代碼解決：** ```java public String replaceSpace(StringBuffer str) { //return str.toString().replaceAll(" ", "%20"); //public String replaceAll(String regex,String replacement) //用給定的替換替換與給定的regular expression匹配的此字符串的每個子字符串。 //\ 轉義字符. 如果你要使用 "\" 本身, 則應該使用 "\\". String類型中的空格用“\s”表示，所以我這里猜測"\\s"就是代表空格的意思 return str.toString().replaceAll("\\s", "%20"); } ``` ### 六 數值的整數次方 #### **題目描述：** 給定一個double類型的浮點數base和int類型的整數exponent。求base的exponent次方。 #### **問題解析：** 這道題算是比較麻煩和難一點的一個了。我這里采用的是**二分冪**思想，當然也可以采用**快速冪**。 更具劍指offer書中細節，該題的解題思路如下： 1.當底數為0且指數<0時，會出現對0求倒數的情況，需進行錯誤處理，設置一個全局變量； 2.判斷底數是否等于0，由于base為double型，所以不能直接用==判斷 3.優化求冪函數（二分冪）。 當n為偶數，a^n =（a^n/2）*（a^n/2）； 當n為奇數，a^n = a^[(n-1)/2] * a^[(n-1)/2] * a。時間復雜度O(logn) **時間復雜度**：O(logn) #### **示例代碼：** ```java public class Solution { boolean invalidInput=false; public double Power(double base, int exponent) { //如果底數等于0并且指數小于0 //由于base為double型，不能直接用==判斷 if(equal(base,0.0)&&exponent<0){ invalidInput=true; return 0.0; } int absexponent=exponent; //如果指數小于0，將指數轉正 if(exponent<0) absexponent=-exponent; //getPower方法求出base的exponent次方。 double res=getPower(base,absexponent); //如果指數小于0，所得結果為上面求的結果的倒數 if(exponent<0) res=1.0/res; return res; } //比較兩個double型變量是否相等的方法 boolean equal(double num1,double num2){ if(num1-num2>-0.000001&&num1-num2<0.000001) return true; else return false; } //求出b的e次方的方法 double getPower(double b,int e){ //如果指數為0，返回1 if(e==0) return 1.0; //如果指數為1，返回b if(e==1) return b; //e>>1相等于e/2，這里就是求a^n =（a^n/2）*（a^n/2） double result=getPower(b,e>>1); result*=result; //如果指數n為奇數，則要再乘一次底數base if((e&1)==1) result*=b; return result; } } ``` 當然這一題也可以采用笨方法：累乘。不過這種方法的時間復雜度為O（n），這樣沒有前一種方法效率高。 ```java // 使用累乘 public double powerAnother(double base, int exponent) { double result = 1.0; for (int i = 0; i < Math.abs(exponent); i++) { result *= base; } if (exponent >= 0) return result; else return 1 / result; } ``` ### 七 調整數組順序使奇數位于偶數前面 #### **題目描述：** 輸入一個整數數組，實現一個函數來調整該數組中數字的順序，使得所有的奇數位于數組的前半部分，所有的偶數位于位于數組的后半部分，并保證奇數和奇數，偶數和偶數之間的相對位置不變。 #### **問題解析：** 這道題有挺多種解法的，給大家介紹一種我覺得挺好理解的方法： 我們首先統計奇數的個數假設為n,然后新建一個等長數組，然后通過循環判斷原數組中的元素為偶數還是奇數。如果是則從數組下標0的元素開始，把該奇數添加到新數組；如果是偶數則從數組下標為n的元素開始把該偶數添加到新數組中。 #### **示例代碼：** 時間復雜度為O（n），空間復雜度為O（n）的算法 ```java public class Solution { public void reOrderArray(int [] array) { //如果數組長度等于0或者等于1，什么都不做直接返回 if(array.length==0||array.length==1) return; //oddCount：保存奇數個數 //oddBegin：奇數從數組頭部開始添加 int oddCount=0,oddBegin=0; //新建一個數組 int[] newArray=new int[array.length]; //計算出（數組中的奇數個數）開始添加元素 for(int i=0;i<array.length;i++){ if((array[i]&1)==1) oddCount++; } for(int i=0;i<array.length;i++){ //如果數為基數新數組從頭開始添加元素 //如果為偶數就從oddCount（數組中的奇數個數）開始添加元素 if((array[i]&1)==1) newArray[oddBegin++]=array[i]; else newArray[oddCount++]=array[i]; } for(int i=0;i<array.length;i++){ array[i]=newArray[i]; } } } ``` ### 八 鏈表中倒數第k個節點 #### **題目描述：** 輸入一個鏈表，輸出該鏈表中倒數第k個結點 #### **問題分析：** **一句話概括：** 兩個指針一個指針p1先開始跑，指針p1跑到k-1個節點后，另一個節點p2開始跑，當p1跑到最后時，p2所指的指針就是倒數第k個節點。 **思想的簡單理解：** 前提假設：鏈表的結點個數(長度)為n。 規律一：要找到倒數第k個結點，需要向前走多少步呢？比如倒數第一個結點，需要走n步，那倒數第二個結點呢？很明顯是向前走了n-1步，所以可以找到規律是找到倒數第k個結點，需要向前走n-k+1步。 **算法開始：** 1. 設兩個都指向head的指針p1和p2，當p1走了k-1步的時候，停下來。p2之前一直不動。 2. p1的下一步是走第k步，這個時候，p2開始一起動了。至于為什么p2這個時候動呢？看下面的分析。 3. 當p1走到鏈表的尾部時，即p1走了n步。由于我們知道p2是在p1走了k-1步才開始動的，也就是說p1和p2永遠差k-1步。所以當p1走了n步時，p2走的應該是在n-(k-1)步。即p2走了n-k+1步，此時巧妙的是p2正好指向的是規律一的倒數第k個結點處。 這樣是不是很好理解了呢？ #### **考察內容：** 鏈表+代碼的魯棒性 #### **示例代碼：** ```java /* //鏈表類 public class ListNode { int val; ListNode next = null; ListNode(int val) { this.val = val; } }*/ //時間復雜度O(n),一次遍歷即可 public class Solution { public ListNode FindKthToTail(ListNode head,int k) { ListNode pre=null,p=null; //兩個指針都指向頭結點 p=head; pre=head; //記錄k值 int a=k; //記錄節點的個數 int count=0; //p指針先跑，并且記錄節點數，當p指針跑了k-1個節點后，pre指針開始跑， //當p指針跑到最后時，pre所指指針就是倒數第k個節點 while(p!=null){ p=p.next; count++; if(k<1){ pre=pre.next; } k--; } //如果節點個數小于所求的倒數第k個節點，則返回空 if(count<a) return null; return pre; } } ``` ### 九 反轉鏈表 #### **題目描述：** 輸入一個鏈表，反轉鏈表后，輸出鏈表的所有元素。 #### **問題分析：** 鏈表的很常規的一道題，這一道題思路不算難，但自己實現起來真的可能會感覺無從下手，我是參考了別人的代碼。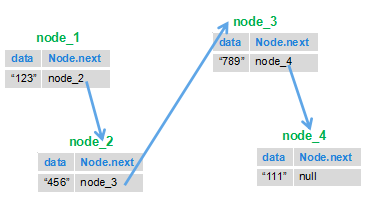 思路就是我們根據鏈表的特點，前一個節點指向下一個節點的特點，把后面的節點移到前面來。 就比如下圖：我們把1節點和2節點互換位置，然后再將3節點指向2節點，4節點指向3節點，這樣以來下面的鏈表就被反轉了。  #### **考察內容：** 鏈表+代碼的魯棒性 #### **示例代碼：** ```java /* public class ListNode { int val; ListNode next = null; ListNode(int val) { this.val = val; } }*/ public class Solution { public ListNode ReverseList(ListNode head) { ListNode next = null; ListNode pre = null; while (head != null) { //保存要反轉到頭來的那個節點 next = head.next; //要反轉的那個節點指向已經反轉的上一個節點 head.next = pre; //上一個已經反轉到頭部的節點 pre = head; //一直向鏈表尾走 head = next; } return pre; } } ``` ### 十 合并兩個排序的鏈表 #### **題目描述：** 輸入兩個單調遞增的鏈表，輸出兩個鏈表合成后的鏈表，當然我們需要合成后的鏈表滿足單調不減規則。 #### **問題分析：** 我們可以這樣分析: 1. 假設我們有兩個鏈表 A,B； 2. A的頭節點A1的值與B的頭結點B1的值比較，假設A1小，則A1為頭節點； 3. A2再和B1比較，假設B1小,則，A1指向B1； 4. A2再和B2比較。。。。。。。 就這樣循環往復就行了，應該還算好理解。 #### **考察內容：** 鏈表+代碼的魯棒性 #### **示例代碼：** **非遞歸版本：** ```java /* public class ListNode { int val; ListNode next = null; ListNode(int val) { this.val = val; } }*/ public class Solution { public ListNode Merge(ListNode list1,ListNode list2) { //list1為空，直接返回list2 if(list1 == null){ return list2; } //list2為空，直接返回list1 if(list2 == null){ return list1; } ListNode mergeHead = null; ListNode current = null; //當list1和list2不為空時 while(list1!=null && list2!=null){ //取較小值作頭結點 if(list1.val <= list2.val){ if(mergeHead == null){ mergeHead = current = list1; }else{ current.next = list1; //current節點保存list1節點的值因為下一次還要用 current = list1; } //list1指向下一個節點 list1 = list1.next; }else{ if(mergeHead == null){ mergeHead = current = list2; }else{ current.next = list2; //current節點保存list2節點的值因為下一次還要用 current = list2; } //list2指向下一個節點 list2 = list2.next; } } if(list1 == null){ current.next = list2; }else{ current.next = list1; } return mergeHead; } } ``` **遞歸版本：** ```java public ListNode Merge(ListNode list1,ListNode list2) { if(list1 == null){ return list2; } if(list2 == null){ return list1; } if(list1.val <= list2.val){ list1.next = Merge(list1.next, list2); return list1; }else{ list2.next = Merge(list1, list2.next); return list2; } } ``` ### 十一 用兩個棧實現隊列 #### **題目描述：** 用兩個棧來實現一個隊列，完成隊列的Push和Pop操作。 隊列中的元素為int類型。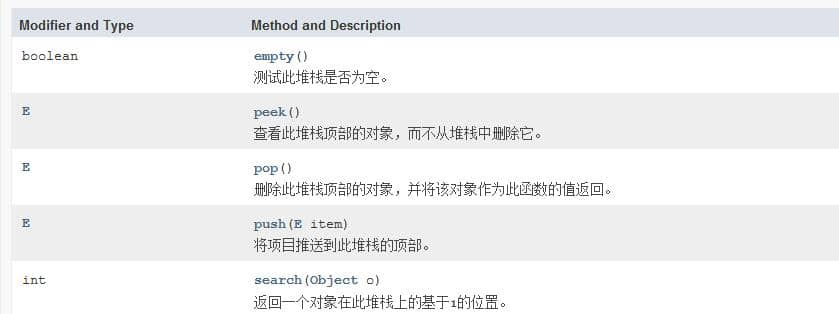 #### 問題分析： 先來回顧一下棧和隊列的基本特點： **棧：**后進先出（LIFO） **隊列：** 先進先出 很明顯我們需要根據JDK給我們提供的棧的一些基本方法來實現。先來看一下Stack類的一些基本方法：  既然題目給了我們兩個棧，我們可以這樣考慮當push的時候將元素push進stack1，pop的時候我們先把stack1的元素pop到stack2，然后再對stack2執行pop操作，這樣就可以保證是先進先出的。（負[pop]負[pop]得正[先進先出]） #### 考察內容： 隊列+棧 #### 示例代碼： ```java //左程云的《程序員代碼面試指南》的答案 import java.util.Stack; public class Solution { Stack<Integer> stack1 = new Stack<Integer>(); Stack<Integer> stack2 = new Stack<Integer>(); //當執行push操作時，將元素添加到stack1 public void push(int node) { stack1.push(node); } public int pop() { //如果兩個隊列都為空則拋出異常,說明用戶沒有push進任何元素 if(stack1.empty()&&stack2.empty()){ throw new RuntimeException("Queue is empty!"); } //如果stack2不為空直接對stack2執行pop操作， if(stack2.empty()){ while(!stack1.empty()){ //將stack1的元素按后進先出push進stack2里面 stack2.push(stack1.pop()); } } return stack2.pop(); } } ``` ### 十二 棧的壓入,彈出序列 #### **題目描述：** 輸入兩個整數序列，第一個序列表示棧的壓入順序，請判斷第二個序列是否為該棧的彈出順序。假設壓入棧的所有數字均不相等。例如序列1,2,3,4,5是某棧的壓入順序，序列4，5,3,2,1是該壓棧序列對應的一個彈出序列，但4,3,5,1,2就不可能是該壓棧序列的彈出序列。（注意：這兩個序列的長度是相等的） #### **題目分析：** 這道題想了半天沒有思路，參考了Alias的答案，他的思路寫的也很詳細應該很容易看懂。 作者：Alias https://www.nowcoder.com/questionTerminal/d77d11405cc7470d82554cb392585106 來源：牛客網 【思路】借用一個輔助的棧，遍歷壓棧順序，先講第一個放入棧中，這里是1，然后判斷棧頂元素是不是出棧順序的第一個元素，這里是4，很顯然1≠4，所以我們繼續壓棧，直到相等以后開始出棧，出棧一個元素，則將出棧順序向后移動一位，直到不相等，這樣循環等壓棧順序遍歷完成，如果輔助棧還不為空，說明彈出序列不是該棧的彈出順序。 舉例： 入棧1,2,3,4,5 出棧4,5,3,2,1 首先1入輔助棧，此時棧頂1≠4，繼續入棧2 此時棧頂2≠4，繼續入棧3 此時棧頂3≠4，繼續入棧4 此時棧頂4＝4，出棧4，彈出序列向后一位，此時為5，,輔助棧里面是1,2,3 此時棧頂3≠5，繼續入棧5 此時棧頂5=5，出棧5,彈出序列向后一位，此時為3，,輔助棧里面是1,2,3 …. 依次執行，最后輔助棧為空。如果不為空說明彈出序列不是該棧的彈出順序。 #### **考察內容：** 棧 #### **示例代碼：** ```java import java.util.ArrayList; import java.util.Stack; //這道題沒想出來，參考了Alias同學的答案：https://www.nowcoder.com/questionTerminal/d77d11405cc7470d82554cb392585106 public class Solution { public boolean IsPopOrder(int [] pushA,int [] popA) { if(pushA.length == 0 || popA.length == 0) return false; Stack<Integer> s = new Stack<Integer>(); //用于標識彈出序列的位置 int popIndex = 0; for(int i = 0; i< pushA.length;i++){ s.push(pushA[i]); //如果棧不為空，且棧頂元素等于彈出序列 while(!s.empty() &&s.peek() == popA[popIndex]){ //出棧 s.pop(); //彈出序列向后一位 popIndex++; } } return s.empty(); } } ```