本文轉載于：labuladong的[單鏈表的六大解題套路](https://mp.weixin.qq.com/s?__biz=MzAxODQxMDM0Mw==&mid=2247492022&idx=1&sn=35f6cb8ab60794f8f52338fab3e5cda5&scene=21#wechat_redirect) 說到單鏈表有很多巧妙的操作，本文就總結一下單鏈表的基本技巧，每個技巧都對應著至少一道算法題： 1、合并兩個有序鏈表 2、合并`k`個有序鏈表 3、尋找單鏈表的倒數第`k`個節點 4、尋找單鏈表的中點 5、判斷單鏈表是否包含環并找出環起點 6、判斷兩個單鏈表是否相交并找出交點 這些解法都用到了雙指針技巧，所以說對于單鏈表相關的題目，雙指針的運用是非常廣泛的，下面我們就來一個一個看。 ### 合并兩個有序鏈表 這是最基本的鏈表技巧，力扣第 21 題「合并兩個有序鏈表」就是這個問題：  給你輸入兩個有序鏈表，請你把他倆合并成一個新的有序鏈表，函數簽名如下： ~~~ ListNode?mergeTwoLists(ListNode?l1,?ListNode?l2); ~~~ 這題比較簡單，我們直接看解法： ``` ListNode?mergeTwoLists(ListNode?l1,?ListNode?l2)?{ //?虛擬頭結點 ????ListNode?dummy?=?new?ListNode(-1),?p?=?dummy; ????ListNode?p1?=?l1,?p2?=?l2; while?(p1?!=?null?&&?p2?!=?null)?{ //?比較?p1?和?p2?兩個指針 //?將值較小的的節點接到?p?指針 if?(p1.val?>?p2.val)?{ ????????????p.next?=?p2; ????????????p2?=?p2.next; ????????}?else?{ ????????????p.next?=?p1; ????????????p1?=?p1.next; ????????} //?p?指針不斷前進 ????????p?=?p.next; ????} if?(p1?!=?null)?{ ????????p.next?=?p1; ????} if?(p2?!=?null)?{ ????????p.next?=?p2; ????} return?dummy.next; } ``` 我們的 while 循環每次比較`p1`和`p2`的大小，把較小的節點接到結果鏈表上：  這個算法的邏輯類似于「拉拉鏈」，`l1, l2`類似于拉鏈兩側的鋸齒，指針`p`就好像拉鏈的拉索，將兩個有序鏈表合并。 **代碼中還用到一個鏈表的算法題中是很常見的「虛擬頭節點」技巧，也就是`dummy`節點**。你可以試試，如果不使用`dummy`虛擬節點，代碼會復雜很多，而有了`dummy`節點這個占位符，可以避免處理空指針的情況，降低代碼的復雜性。 ### 合并 k 個有序鏈表 看下力扣第 23 題「合并K個升序鏈表」：  函數簽名如下： ~~~ ListNode?mergeKLists(ListNode[]?lists); ~~~ 合并`k`個有序鏈表的邏輯類似合并兩個有序鏈表，難點在于，如何快速得到`k`個節點中的最小節點，接到結果鏈表上？ 這里我們就要用到[優先級隊列（二叉堆）](https://mp.weixin.qq.com/s?__biz=MzAxODQxMDM0Mw==&mid=2247484495&idx=1&sn=bbfeba9bb5cfd50598e2a4d08c839ee9&scene=21#wechat_redirect)這種數據結構，把鏈表節點放入一個最小堆，就可以每次獲得`k`個節點中的最小節點： ``` ListNode?mergeKLists(ListNode\[\]?lists)?{ if?(lists.length?==?0)?returnnull; //?虛擬頭結點 ????ListNode?dummy?=?new?ListNode(-1); ????ListNode?p?=?dummy; //?優先級隊列，最小堆 ????PriorityQueue?pq?=?new?PriorityQueue<>( ????????lists.length,?(a,?b)->(a.val?-?b.val)); //?將?k?個鏈表的頭結點加入最小堆 for?(ListNode?head?:?lists)?{ if?(head?!=?null) ????????????pq.add(head); ????} while?(!pq.isEmpty())?{ //?獲取最小節點，接到結果鏈表中 ????????ListNode?node?=?pq.poll(); ????????p.next?=?node; if?(node.next?!=?null)?{ ????????????pq.add(node.next); ????????} //?p?指針不斷前進 ????????p?=?p.next; ????} return?dummy.next; } ``` 這個算法是面試常考題，它的時間復雜度是多少呢？ 優先隊列`pq`中的元素個數最多是`k`，所以一次`poll`或者`add`方法的時間復雜度是`O(logk)`；所有的鏈表節點都會被加入和彈出`pq`，**所以算法整體的時間復雜度是`O(Nlogk)`，其中`k`是鏈表的條數，`N`是這些鏈表的節點總數**。 ### 單鏈表的倒數第 k 個節點 從前往后尋找單鏈表的第`k`個節點很簡單，一個 for 循環遍歷過去就找到了，但是如何尋找從后往前數的第`k`個節點呢？ 那你可能說，假設鏈表有`n`個節點，倒數第`k`個節點就是正數第`n - k`個節點，不也是一個 for 循環的事兒嗎？ 是的，但是算法題一般只給你一個`ListNode`頭結點代表一條單鏈表，你不能直接得出這條鏈表的長度`n`，而需要先遍歷一遍鏈表算出`n`的值，然后再遍歷鏈表計算第`n - k`個節點。 也就是說，這個解法需要遍歷兩次鏈表才能得到出倒數第`k`個節點。 那么，我們能不能**只遍歷一次鏈表**，就算出倒數第`k`個節點？可以做到的，如果是面試問到這道題，面試官肯定也是希望你給出只需遍歷一次鏈表的解法。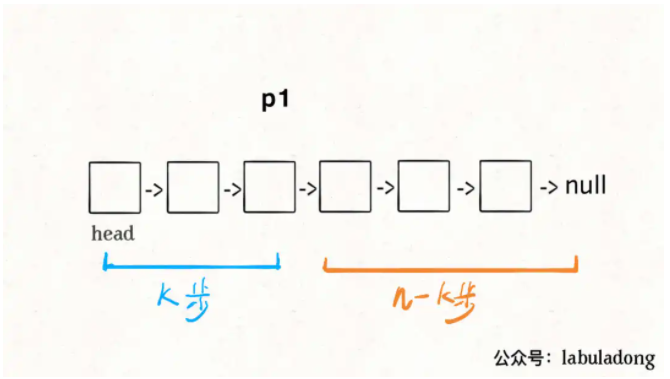 這個解法就比較巧妙了，假設`k = 2`，思路如下： 首先，我們先讓一個指針`p1`指向鏈表的頭節點`head`，然后走`k`步：  現在的`p1`，只要再走`n - k`步，就能走到鏈表末尾的空指針了對吧？ 趁這個時候，再用一個指針`p2`指向鏈表頭節點`head`：  接下來就很顯然了，讓`p1`和`p2`同時向前走，`p1`走到鏈表末尾的空指針時走了`n - k`步，`p2`也走了`n - k`步，也就恰好到達了鏈表的倒數第`k`個節點：  這樣，只遍歷了一次鏈表，就獲得了倒數第`k`個節點`p2`。 上述邏輯的代碼如下： ``` //?返回鏈表的倒數第?k?個節點 ListNode?findFromEnd(ListNode?head,?int?k)?{ ????ListNode?p1?=?head; //?p1?先走?k?步 for?(int?i?=?0;?i?<?k;?i++)?{ ????????p1?=?p1.next; ????} ????ListNode?p2?=?head; //?p1?和?p2?同時走?n?-?k?步 while?(p1?!=?null)?{ ????????p2?=?p2.next; ????????p1?=?p1.next; ????} //?p2?現在指向第?n?-?k?個節點 return?p2; } ``` 當然，如果用 big O 表示法來計算時間復雜度，無論遍歷一次鏈表和遍歷兩次鏈表的時間復雜度都是`O(N)`，但上述這個算法更有技巧性。 很多鏈表相關的算法題都會用到這個技巧，比如說力扣第 19 題「刪除鏈表的倒數第 N 個結點」：  我們直接看解法代碼： ``` //?主函數 public?ListNode?removeNthFromEnd(ListNode?head,?int?n)?{ //?虛擬頭節點 ????ListNode?dummy?=?new?ListNode(-1); ????dummy.next?=?head; //?刪除倒數第?n?個，要先找倒數第?n?+?1?個節點 ????ListNode?x?=?findFromEnd(dummy,?n?+?1); //?刪掉倒數第?n?個節點 ????x.next?=?x.next.next; return?dummy.next; } private?ListNode?findFromEnd(ListNode?head,?int?k)?{ //?代碼見上文 } ``` 這個邏輯就很簡單了，要刪除倒數第`n`個節點，就得獲得倒數第`n + 1`個節點的引用，可以用我們實現的`findFromEnd`來操作。 不過注意我們又使用了虛擬頭結點的技巧，也是為了防止出現空指針的情況，比如說鏈表總共有 5 個節點，題目就讓你刪除倒數第 5 個節點，也就是第一個節點，那按照算法邏輯，應該首先找到倒數第 6 個節點。但第一個節點前面已經沒有節點了，這就會出錯。 但有了我們虛擬節點`dummy`的存在，就避免了這個問題，能夠對這種情況進行正確的刪除。 ### 單鏈表的中點 力扣第 876 題「鏈表的中間結點」就是這個題目，問題的關鍵也在于我們無法直接得到單鏈表的長度`n`，常規方法也是先遍歷鏈表計算`n`，再遍歷一次得到第`n / 2`個節點，也就是中間節點。 如果想一次遍歷就得到中間節點，也需要耍點小聰明，使用「快慢指針」的技巧： 我們讓兩個指針`slow`和`fast`分別指向鏈表頭結點`head`。 **每當慢指針`slow`前進一步，快指針`fast`就前進兩步，這樣，當`fast`走到鏈表末尾時，`slow`就指向了鏈表中點**。 上述思路的代碼實現如下： ``` ListNode?middleNode(ListNode?head)?{ //?快慢指針初始化指向?head ????ListNode?slow?=?head,?fast?=?head; //?快指針走到末尾時停止 while?(fast?!=?null?&&?fast.next?!=?null)?{ //?慢指針走一步，快指針走兩步 ????????slow?=?slow.next; ????????fast?=?fast.next.next; ????} //?慢指針指向中點 return?slow; } ``` 需要注意的是，如果鏈表長度為偶數，也就是說中點有兩個的時候，我們這個解法返回的節點是靠后的那個節點。 另外，這段代碼稍加修改就可以直接用到判斷鏈表成環的算法題上。 ### 判斷鏈表是否包含環 判斷單鏈表是否包含環屬于經典問題了，解決方案也是用快慢指針： 每當慢指針`slow`前進一步，快指針`fast`就前進兩步。 如果`fast`最終遇到空指針，說明鏈表中沒有環；如果`fast`最終和`slow`相遇，那肯定是`fast`超過了`slow`一圈，說明鏈表中含有環。 只需要把尋找鏈表中點的代碼稍加修改就行了： ``` boolean?hasCycle(ListNode?head)?{ //?快慢指針初始化指向?head ????ListNode?slow?=?head,?fast?=?head; //?快指針走到末尾時停止 while?(fast?!=?null?&&?fast.next?!=?null)?{ //?慢指針走一步，快指針走兩步 ????????slow?=?slow.next; ????????fast?=?fast.next.next; //?快慢指針相遇，說明含有環 if?(slow?==?fast)?{ returntrue; ????????} ????} //?不包含環 returnfalse; } ``` 當然，這個問題還有進階版：如果鏈表中含有環，如何計算這個環的起點？  這里簡單提一下解法： ``` ListNode?detectCycle(ListNode?head)?{ ????ListNode?fast,?slow; ????fast?=?slow?=?head; while?(fast?!=?null?&&?fast.next?!=?null)?{ ????????fast?=?fast.next.next; ????????slow?=?slow.next; if?(fast?==?slow)?break; ????} //?上面的代碼類似?hasCycle?函數 if?(fast?==?null?||?fast.next?==?null)?{ //?fast?遇到空指針說明沒有環 returnnull; ????} //?重新指向頭結點 ????slow?=?head; //?快慢指針同步前進，相交點就是環起點 while?(slow?!=?fast)?{ ????????fast?=?fast.next; ????????slow?=?slow.next; ????} return?slow; } ``` 可以看到，當快慢指針相遇時，讓其中任一個指針指向頭節點，然后讓它倆以相同速度前進，再次相遇時所在的節點位置就是環開始的位置。 我們假設快慢指針相遇時，慢指針`slow`走了`k`步，那么快指針`fast`一定走了`2k`步：  **`fast`一定比`slow`多走了`k`步，這多走的`k`步其實就是`fast`指針在環里轉圈圈，所以`k`的值就是環長度的「整數倍」**。 假設相遇點距環的起點的距離為`m`，那么結合上圖的?slow指針，環的起點距頭結點`head`的距離為`k - m`，也就是說如果從`head`前進`k - m`步就能到達環起點。 巧的是，如果從相遇點繼續前進`k - m`步，也恰好到達環起點。因為結合上圖的?fast指針，從相遇點開始走`k`步可以轉回到相遇點，那走`k - m`步肯定就走到環起點了：  所以，只要我們把快慢指針中的任一個重新指向`head`，然后兩個指針同速前進，`k - m`步后一定會相遇，相遇之處就是環的起點了。 ### 兩個鏈表是否相交 這個問題有意思，也是力扣第 160 題「相交鏈表」函數簽名如下： ~~~ ListNode?getIntersectionNode(ListNode?headA,?ListNode?headB); ~~~ 給你輸入兩個鏈表的頭結點`headA`和`headB`，這兩個鏈表可能存在相交。 如果相交，你的算法應該返回相交的那個節點；如果沒相交，則返回 null。 比如題目給我們舉的例子，如果輸入的兩個鏈表如下圖：  那么我們的算法應該返回`c1`這個節點。 這個題直接的想法可能是用`HashSet`記錄一個鏈表的所有節點，然后和另一條鏈表對比，但這就需要額外的空間。 如果不用額外的空間，只使用兩個指針，你如何做呢？ 難點在于，由于兩條鏈表的長度可能不同，兩條鏈表之間的節點無法對應：  如果用兩個指針`p1`和`p2`分別在兩條鏈表上前進，并不能**同時**走到公共節點，也就無法得到相交節點`c1`。 **所以，解決這個問題的關鍵是，通過某些方式，讓`p1`和`p2`能夠同時到達相交節點`c1`**。 所以，我們可以讓`p1`遍歷完鏈表`A`之后開始遍歷鏈表`B`，讓`p2`遍歷完鏈表`B`之后開始遍歷鏈表`A`，這樣相當于「邏輯上」兩條鏈表接在了一起。 如果這樣進行拼接，就可以讓`p1`和`p2`同時進入公共部分，也就是同時到達相交節點`c1`：  那你可能會問，如果說兩個鏈表沒有相交點，是否能夠正確的返回 null 呢？ 這個邏輯可以覆蓋這種情況的，相當于`c1`節點是 null 空指針嘛，可以正確返回 null。 按照這個思路，可以寫出如下代碼： ``` ListNode?getIntersectionNode(ListNode?headA,?ListNode?headB)?{ //?p1?指向?A?鏈表頭結點，p2?指向?B?鏈表頭結點 ????ListNode?p1?=?headA,?p2?=?headB; while?(p1?!=?p2)?{ //?p1?走一步，如果走到?A?鏈表末尾，轉到?B?鏈表 if?(p1?==?null)?p1?=?headB; else????????????p1?=?p1.next; //?p2?走一步，如果走到?B?鏈表末尾，轉到?A?鏈表 if?(p2?==?null)?p2?=?headA; else????????????p2?=?p2.next; ????} return?p1; } ``` 這樣，這道題就解決了，空間復雜度為`O(1)`，時間復雜度為`O(N)`。 以上就是單鏈表的所有技巧，希望對你有啟發。