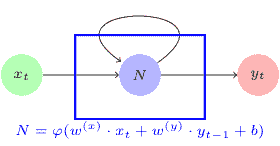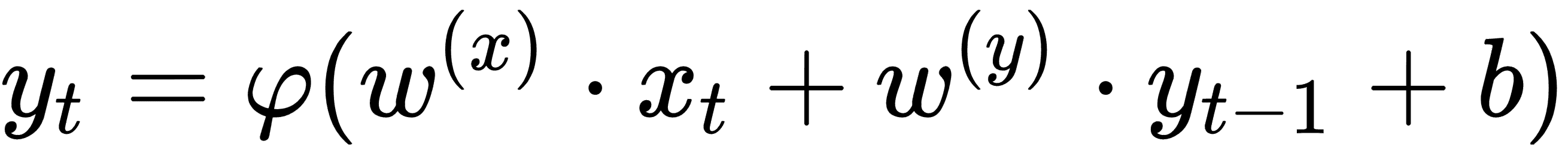
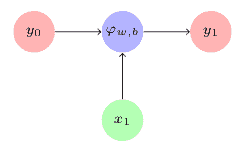
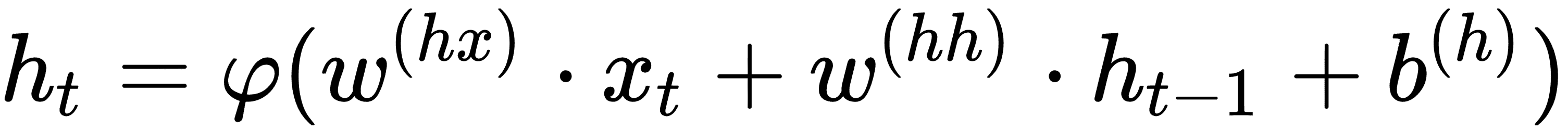
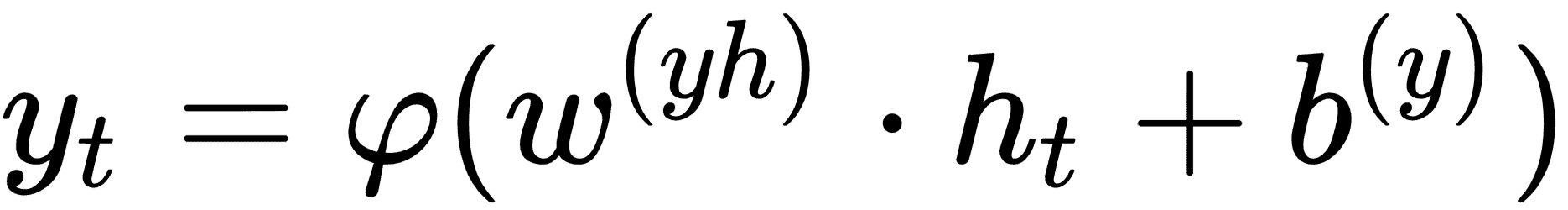
# 簡單循環神經網絡 這是一個帶循環的簡單神經網絡： RNN Network 在該圖中，神經網絡`N`接受輸入`x[t]`以產生輸出`y[t]`。由于循環，在下一步`t+1`，輸入`y[t]`和輸入`x[t+1]`產生輸出`y[t+1]`。在數學上，我們將其表示為以下等式：  當我們展開循環時，RNN 架構在時間步`t1`看起來如下：  隨著時間步長的發展，這個循環在時間步驟 5 展開如下：  在每個時間步驟，使用相同的學習函數`φ(·)`和相同的參數，`w`和`b`。 輸出`y`并不總是在每個時間步產生。相反，在每個時間步產生輸出`h`，并且對該輸出`h`應用另一個激活函數以產生輸出`y`。 RNN 的等式現在看起來像這樣：   其中， * `w(hx)`是連接到隱藏層的`x`輸入的權重向量 * `w(hh)`是來自前一時間步的`h`的值的權重向量 * `w(yh)`是連接隱藏層和輸出層的層的權重向量 * 用于`h[t]`的函數通常是非線性函數，例如 tanh 或 ReLU 在 RNN 中，在每個時間步使用相同的參數`w(hx), w(hh), w(yh), b(h), b(y)`。這一事實大大減少了我們需要學習的基于序列模型的參數數量。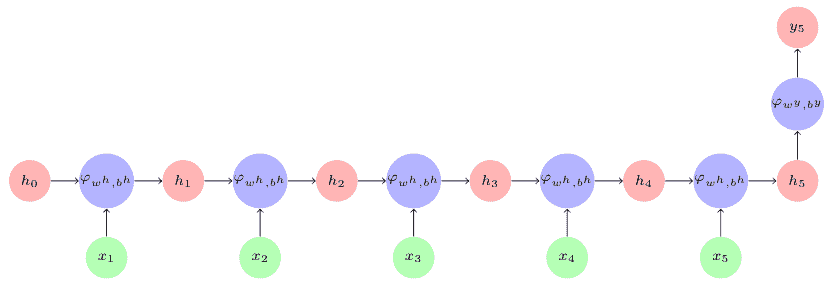 由此， RNN 在時間步`t5`如下展開，假設輸出`y`僅在時間步`t5`產生：  簡單的 RNN 由 Elman 在 1990 年引入，因此它也被稱為 Elman 網絡。然而，簡單的 RNN 無法滿足我們今天的處理需求，因此我們將在下一節中了解 RNN 的變體。 閱讀 Elman 的原始研究論文，了解 RNN 架構的起源： ``` J. L. Elman, Finding Structure in Time, Cogn. Sci., vol. 14, no. 2, pp. 179–211, 1990. ```