[TOC]
# 概念
斐波那契數列是以下一系列數字:
> 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ...
<br>
在種子數字 0 和 1 之后,后續的每一個數字都是前面兩個數字之和。
<br>
斐波那契數列的一個有趣的性質是,數列的當前數字與前一個數字的比值無限趨近于黃金分割數, 1.61803398875…
你可以使用斐波那契數列來生成各種各樣有趣的東西,比如黃金螺旋 (Golden Spiral),自然界中存在許多黃金螺旋。
<br>
<br>
斐波那契數列(意大利語:Successione di Fibonacci),又譯為費波拿契數、費氏數列、黃金分割數列。
<br>
在數學上,斐波那契數列是以遞歸的方法來定義:
<br>
> F(0)=0, F(1)=1, n>1時,F(n)=F(n-1)+F(n-2)。
<br>
根據該規則,返回第n個斐波那契數。
<br>
<br>
# 實現
## 遞歸法
~~~jsx
function fibonacci(n) {
if(n === 0 || n === 1) {
return n;
}
console.log(`fibonacci(${n-1}) + fibonacci(${n-2})`)
return fibonacci(n - 2) + fibonacci(n - 1)
}
fibonacci(5)
~~~
思路:不斷調用自身方法,直到n為1或0之后,開始一層層返回數據。
問題:使用遞歸計算大數字時,性能會非常低;另外,遞歸造成了大量的重復計算(很多函數執行了多次)。
<br>
<br>
## 數組緩存
從上面代碼的 console 中可以看出,執行了許多相同的運算。如果我們對中間求得的變量值,進行存儲的話,就會大大減少函數被調用的次數。
這是典型的以空間換時間。很明顯,函數被調用的次數大大減少,耗時明顯縮減。
~~~jsx
let fibonacci = function() {
let temp = [0, 1];
return function(n) {
let result = temp[n];
if(typeof result != 'number') {
result = fibonacci(n - 1) + fibonacci(n - 2);
temp[n] = result; // 將每次 fibonacci(n) 的值都緩存下來
}
return result;
}
}(); // 外層立即執行
~~~
<br>
<br>
## 遞推法(動態規劃)
動態規劃:從底部開始解決問題,將所有小問題解決掉,然后合并成一個整體解決方案,從而解決掉整個大問題;
遞歸:從頂部開始將問題分解,通過解決掉所有分解的小問題來解決整個問題;
~~~jsx
function fibonacci(n) {
let current = 0;
let next = 1;
let temp;
for(let i = 0; i < n; i++) {
temp = current;
current = next;
next += temp;
}
console.log(`fibonacci(${n}, ${next}, ${current + next})`);
return current;
}
~~~
思路:從下往上計算,首先根據f(0)和f(1)算出f(2),再根據f(1)和f(2)算出f(3),依次類推我們就可以算出第n項了。
而這種算法的時間復雜度僅為O(n),比遞歸函數的寫法效率要大大增強。
1. 寫法一:
~~~jsx
function fib(n) {
let current = 0;
let next = 1;
for(let i = 0; i < n; i++) {
[current, next] = [next, current + next];
}
return current;
}
~~~
[\[解構賦值\]](https://developer.mozilla.org/zh-CN/docs/Web/JavaScript/Reference/Operators/Destructuring_assignment)允許我們將值直接從數組中提取到不同變量中。因此我們可以用解構賦值,省略temp中間變量。
2. 寫法二:
~~~jsx
function fib(n) {
let current = 0;
let next = 1;
while(n --> 0) { // while(n>0) {n--} n--的返回值是n
[current, next] = [next, current + next];
}
return current;
}
fib(10)
~~~
<br>
<br>
## 尾調用優化
~~~jsx
// 在ES6規范中,有一個尾調用優化,可以實現高效的尾遞歸方案。
// ES6的尾調用優化只在嚴格模式下開啟,正常模式是無效的。
'use strict'
function fib(n, current = 0, next = 1) {
if(n == 0) return 0;
if(n == 1) return next; // return next
console.log(`fibonacci(${n}, ${next}, ${current + next})`);
return fib(n - 1, next, current + next);
}
~~~
* * *
<br>
<br>
\=======下面是科普======
# 什么是尾調用
一句話,就是指某個函數的最后一步是調用另一個函數。
~~~jsx
// 用代碼來說,就是B函數的返回值被A函數返回了。
function B() {
return 1;
}
function A() {
return B(); // return 1
}
// 尾調用不一定出現在函數尾部,只要是最后一步操作即可
function f(x) {
if (x > 0) {
return m(x)
}
return n(x);
}
// 下面不屬于尾調用:調用函數g之后,還有別的操作
function f(x){
let y = g(x);
return y;
}
function f(x){
return g(x) + 1;
}
function f(x) {
g(x); // 這一步相當于g(x) return undefined
}
~~~
# 尾調用優化
了解 js 的調用棧我們知道,當腳本要調用一個函數時,解析器把該函數添加到棧中并且執行這個函數,并形成一個棧幀(調用幀),保存調用位置和內部變量等信息。
<br>
如果在函數A的內部調用函數B,那么在A的調用幀上方,還會形成一個B的調用幀。等到B運行結束,將結果返回到A,B的調用幀才會銷毀。此時如果函數B內部還調用函數C,那就還有一個C的調用幀,以此類推。例如遞歸操作,一個調用棧中如果保存了大量的棧幀,調用棧非常長,消耗了巨大的內存,會導致爆棧(棧溢出,stack overflow)。**后入先出**的結構。
<br>
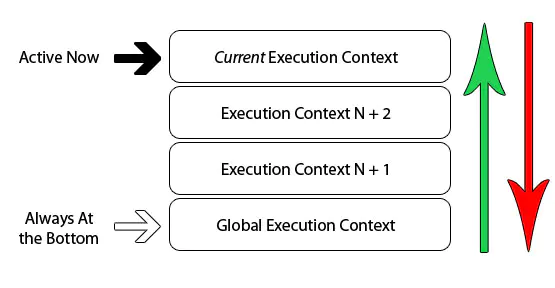
<br>
當函數內部調用函數時,會在棧頂壓入一個調用幀,該函數執行完后,彈出棧,接著再執行棧頂的調用幀。
<br>
尾調用之所以與其他調用不同,就在于它的特殊的調用位置。
<br>
那么現在,我們使用尾調用的話,將函數B放到了函數A的最后一步調用,**內層函數不引用外層函數的變量**,就不用保留外層變量的調用幀了。這樣的話內層函數的調用幀,會直接取代外層函數的調用幀。調用棧的長度就會小很多。
<br>
當然,如果內層函數B使用了外層函數A的變量,那么就仍然需要保留函數A的棧幀,典型例子即是閉包。
~~~jsx
function f() {
let m = 1;
let n = 2;
return g(m + n);
}
f();
~~~
這應當是一次尾調用。因為m+n的值是通過參數傳入函數g內部,并沒有直接引用,因此也不能說保存 f 內部的變量的值。
<br>
下面這種情況內層函數會引用外層函數的值,所以當執行到內層函數時外層函數的調用幀還會存在與當前調用棧中。
~~~jsx
function f() {
let m = 1;
let n = 2;
return function() {
return m+n;
};
}
f();
~~~
總得來說,如果所有函數的調用都是尾調用,即只保留內層函數的調用幀,做到每次執行時(例如遞歸操作),一個調用棧中調用幀只有一項,那么調用棧的長度就會小很多,這樣需要占用的內存也會大大減少。這就是尾調用優化的含義。
<br>
# 什么時候會開啟尾調用優化
在ES5中,尾調用和其他形式的函數調用一樣:腳本引擎創建一個新的函數棧幀并且壓在當前調用的函數的棧幀上面。也就是說,在整個函數棧上,每一個函數棧幀都會被保存,這有可能造成調用棧占用內存過大甚至溢出。
<br>
在ES6中,strict模式下,滿足以下條件,尾調用優化會開啟,此時引擎不會創建一個新的棧幀,而是清除當前棧幀的數據并復用:
* 尾調用函數不需要訪問當前棧幀中的變量;
* 尾調用返回后,函數沒有語句需要繼續執行;
* 尾調用的結果就是函數的返回值;
<br>
ES6的尾調用優化只在嚴格模式下開啟,正常模式是無效的。
這是因為在正常模式下,函數內部有兩個變量,可以跟蹤函數的調用棧。
> arguments:返回調用時函數的參數。
> func.caller:返回調用當前函數的那個函數。
<br>
尾調用優化發生時,函數的調用棧會改寫,因此上面兩個變量就會失真。嚴格模式禁用這兩個變量,所以尾調用模式僅在嚴格模式下生效。
<br>
<br>
# 尾遞歸
函數調用自身,稱為遞歸。如果尾調用自身,就稱為尾遞歸。
<br>
遞歸非常耗費內存,因為需要同時保存成千上百個調用幀,很容易發生"棧溢出"錯誤(stack overflow)。但對于尾遞歸來說,由于只存在一個調用幀,所以永遠不會發生"棧溢出"錯誤。
<br>
由此可見,"尾調用優化"對遞歸操作意義重大。
<br>
<br>
# 遞歸函數的改寫
尾遞歸的實現,往往需要改寫遞歸函數,確保最后一步只調用自身。做到這一點的方法,就是把所有用到的內部變量改寫成函數的參數。
<br>
例如實現 fibonacci 函數需要用到兩個中間變量 current 和 next,那就把這個中間變量改寫成函數的參數。
~~~jsx
// 實現階乘 復雜度 O(n)
function factorial(n) {
if (n === 1) return 1;
return n * factorial(n - 1);
}
// 尾遞歸 只保留一個調用幀,復雜度 O(1)
function factorial(n, total = 1) {
if (n === 1) return total;
console.log(`${n}*${total}`,n*total);
return factorial(n - 1, n * total);
}
~~~
<br>
# 問題
* 在V8引擎層面消除尾遞歸是一個隱式的行為,程序員寫代碼時可能意識不到自己寫了死循環的尾遞歸,而出現死循環后又不會報出stack overflow的錯誤,難以辨別。
* 堆棧信息會在優化的過程中丟失,開發者調試非常困難。
# 參考資料
[js 實現斐波那契數列(數組緩存、動態規劃、尾調用優化)](https://www.jianshu.com/p/bbc7e54a98d6)
- 第一部分 HTML
- meta
- meta標簽
- HTML5
- 2.1 語義
- 2.2 通信
- 2.3 離線&存儲
- 2.4 多媒體
- 2.5 3D,圖像&效果
- 2.6 性能&集成
- 2.7 設備訪問
- SEO
- Canvas
- 壓縮圖片
- 制作圓角矩形
- 全局屬性
- 第二部分 CSS
- CSS原理
- 層疊上下文(stacking context)
- 外邊距合并
- 塊狀格式化上下文(BFC)
- 盒模型
- important
- 樣式繼承
- 層疊
- 屬性值處理流程
- 分辨率
- 視口
- CSS API
- grid(未完成)
- flex
- 選擇器
- 3D
- Matrix
- AT規則
- line-height 和 vertical-align
- CSS技術
- 居中
- 響應式布局
- 兼容性
- 移動端適配方案
- CSS應用
- CSS Modules(未完成)
- 分層
- 面向對象CSS(未完成)
- 布局
- 三列布局
- 單列等寬,其他多列自適應均勻
- 多列等高
- 圣杯布局
- 雙飛翼布局
- 瀑布流
- 1px問題
- 適配iPhoneX
- 橫屏適配
- 圖片模糊問題
- stylelint
- 第三部分 JavaScript
- JavaScript原理
- 內存空間
- 作用域
- 執行上下文棧
- 變量對象
- 作用域鏈
- this
- 類型轉換
- 閉包(未完成)
- 原型、面向對象
- class和extend
- 繼承
- new
- DOM
- Event Loop
- 垃圾回收機制
- 內存泄漏
- 數值存儲
- 連等賦值
- 基本類型
- 堆棧溢出
- JavaScriptAPI
- document.referrer
- Promise(未完成)
- Object.create
- 遍歷對象屬性
- 寬度、高度
- performance
- 位運算
- tostring( ) 與 valueOf( )方法
- JavaScript技術
- 錯誤
- 異常處理
- 存儲
- Cookie與Session
- ES6(未完成)
- Babel轉碼
- let和const命令
- 變量的解構賦值
- 字符串的擴展
- 正則的擴展
- 數值的擴展
- 數組的擴展
- 函數的擴展
- 對象的擴展
- Symbol
- Set 和 Map 數據結構
- proxy
- Reflect
- module
- AJAX
- ES5
- 嚴格模式
- JSON
- 數組方法
- 對象方法
- 函數方法
- 服務端推送(未完成)
- JavaScript應用
- 復雜判斷
- 3D 全景圖
- 重載
- 上傳(未完成)
- 上傳方式
- 文件格式
- 渲染大量數據
- 圖片裁剪
- 斐波那契數列
- 編碼
- 數組去重
- 淺拷貝、深拷貝
- instanceof
- 模擬 new
- 防抖
- 節流
- 數組扁平化
- sleep函數
- 模擬bind
- 柯里化
- 零碎知識點
- 第四部分 進階
- 計算機原理
- 數據結構(未完成)
- 算法(未完成)
- 排序算法
- 冒泡排序
- 選擇排序
- 插入排序
- 快速排序
- 搜索算法
- 動態規劃
- 二叉樹
- 瀏覽器
- 瀏覽器結構
- 瀏覽器工作原理
- HTML解析
- CSS解析
- 渲染樹構建
- 布局(Layout)
- 渲染
- 瀏覽器輸入 URL 后發生了什么
- 跨域
- 緩存機制
- reflow(回流)和repaint(重繪)
- 渲染層合并
- 編譯(未完成)
- Babel
- 設計模式(未完成)
- 函數式編程(未完成)
- 正則表達式(未完成)
- 性能
- 性能分析
- 性能指標
- 首屏加載
- 優化
- 瀏覽器層面
- HTTP層面
- 代碼層面
- 構建層面
- 移動端首屏優化
- 服務器層面
- bigpipe
- 構建工具
- Gulp
- webpack
- Webpack概念
- Webpack工具
- Webpack優化
- Webpack原理
- 實現loader
- 實現plugin
- tapable
- Webpack打包后代碼
- rollup.js
- parcel
- 模塊化
- ESM
- 安全
- XSS
- CSRF
- 點擊劫持
- 中間人攻擊
- 密碼存儲
- 測試(未完成)
- 單元測試
- E2E測試
- 框架測試
- 樣式回歸測試
- 異步測試
- 自動化測試
- PWA
- PWA官網
- web app manifest
- service worker
- app install banners
- 調試PWA
- PWA教程
- 框架
- MVVM原理
- Vue
- Vue 餓了么整理
- 樣式
- 技巧
- Vue音樂播放器
- Vue源碼
- Virtual Dom
- computed原理
- 數組綁定原理
- 雙向綁定
- nextTick
- keep-alive
- 導航守衛
- 組件通信
- React
- Diff 算法
- Fiber 原理
- batchUpdate
- React 生命周期
- Redux
- 動畫(未完成)
- 異常監控、收集(未完成)
- 數據采集
- Sentry
- 貝塞爾曲線
- 視頻
- 服務端渲染
- 服務端渲染的利與弊
- Vue SSR
- React SSR
- 客戶端
- 離線包
- 第五部分 網絡
- 五層協議
- TCP
- UDP
- HTTP
- 方法
- 首部
- 狀態碼
- 持久連接
- TLS
- content-type
- Redirect
- CSP
- 請求流程
- HTTP/2 及 HTTP/3
- CDN
- DNS
- HTTPDNS
- 第六部分 服務端
- Linux
- Linux命令
- 權限
- XAMPP
- Node.js
- 安裝
- Node模塊化
- 設置環境變量
- Node的event loop
- 進程
- 全局對象
- 異步IO與事件驅動
- 文件系統
- Node錯誤處理
- koa
- koa-compose
- koa-router
- Nginx
- Nginx配置文件
- 代理服務
- 負載均衡
- 獲取用戶IP
- 解決跨域
- 適配PC與移動環境
- 簡單的訪問限制
- 頁面內容修改
- 圖片處理
- 合并請求
- PM2
- MongoDB
- MySQL
- 常用MySql命令
- 自動化(未完成)
- docker
- 創建CLI
- 持續集成
- 持續交付
- 持續部署
- Jenkins
- 部署與發布
- 遠程登錄服務器
- 增強服務器安全等級
- 搭建 Nodejs 生產環境
- 配置 Nginx 實現反向代理
- 管理域名解析
- 配置 PM2 一鍵部署
- 發布上線
- 部署HTTPS
- Node 應用
- 爬蟲(未完成)
- 例子
- 反爬蟲
- 中間件
- body-parser
- connect-redis
- cookie-parser
- cors
- csurf
- express-session
- helmet
- ioredis
- log4js(未完成)
- uuid
- errorhandler
- nodeclub源碼
- app.js
- config.js
- 消息隊列
- RPC
- 性能優化
- 第七部分 總結
- Web服務器
- 目錄結構
- 依賴
- 功能
- 代碼片段
- 整理
- 知識清單、博客
- 項目、組件、庫
- Node代碼
- 面試必考
- 91算法
- 第八部分 工作代碼總結
- 樣式代碼
- 框架代碼
- 組件代碼
- 功能代碼
- 通用代碼
