# 0.2 什么是微積分？我們為什么要研究它？ > 原文： [http://math.mit.edu/~djk/calculus_beginners/chapter00/section02.html](http://math.mit.edu/~djk/calculus_beginners/chapter00/section02.html) 微積分是對事物變化的研究。它為有變化的系統建模提供了框架，并提供了推斷這些模型預測的方法。 **我已經存在了一段時間，并且知道事情的變化，或多或少。微積分可以添加什么？** 我相信你對事情的變化了解很多。你有一個定性的微積分概念。例如，運動速度的概念是直接來自微積分的概念，盡管它在微積分之前確實存在很久并且你對它有很多了解。 **那么微積分為我增添了什么？** 它為我們提供了一種構建相對簡單的變化定量模型并推斷其后果的方法。 **到底是什么？** 通過這種方式，您可以在正在調查的系統中找到不斷變化的條件的影響。通過研究這些，您可以學習如何控制系統，讓它做你想做的事。微積分，通過為工程師和您提供建模和控制系統的能力，使他們（可能還有你）在物質世界中擁有非凡的力量。 微積分的發展及其在物理和工程中的應用可能是現代科學發展中最重要的因素，超越阿基米德時代。這是工業革命的主要原因，也是隨之而來的一切，包括過去幾個世紀幾乎所有的重大進步。 **你是否試圖聲稱我對微積分有足夠的了解模型系統并推導出足以控制它們的程度？** 如果你在 1990 年問我這個問題，我會說不。現在，對于一些非平凡的系統，使用筆記本電腦或臺式電腦是可能的。 **好的，但微積分模型如何變化？什么是微積分？** 微積分的基本思想是通過研究“瞬時”變化來研究變化，我們指的是在很短的時間間隔內的變化。 **這有什么用？** 事實證明，這種變化往往比有限時間間隔內的變化簡單得多。這意味著它們更容易建模。實際上微積分是由牛頓發明的，他發現加速度，即物體速度的變化可以用他相對簡單的運動定律來模擬。 **等等？** 這使我們面臨的問題是從關于速度或加速度的信息中推導出關于物體運動的信息。微積分的細節涉及速度和加速度所代表的概念與位置所代表的概念之間的相互關系。 **那么學習微積分的研究是什么？** 首先，您必須有一個框架來描述位置速度和加速度等概念。 單變量微積分是我們開始的，它可以處理物體沿固定路徑的運動。更常見的問題是，當運動可以在表面上或在空間中發生時，可以通過多變量微積分來處理。我們通過找到使用一維思想和方法來處理更一般問題的巧妙技巧來研究后一個主題。因此單變量微積分也是一般問題的關鍵。 當我們處理沿著路徑移動的物體時，它的位置隨時間變化我們可以隨時用一個數字描述它的位置，這可以是某些單位距離該路徑上某個固定點的距離，稱為我們的原點。坐標系。 （我們在此距離上添加一個符號，如果對象位于原點后面，則為負數。） 然后，物體的運動由相關時間點處的數值位置的集合來表征。 我們用來描述運動的位置和時間集就是我們所說的**函數**。類似的函數用于描述應用微積分的所有系統中感興趣的量。 這里的課程首先回顧數字和函數及其屬性。毫無疑問，您對此非常熟悉，因此我們嘗試添加不熟悉的材料以便在查看時保持您的注意力。 **如果我讀到這些東西，我會陷入困境。我必須嗎？** 我很樂意讓你看看它，因為我寫了它，但如果你不愿意，你可以毫無疑問地通過跳過它，并在你需要的時候或者如果你需要這樣做的時候再回過頭來。但是你會錯過這些新信息，這樣做可能會讓你永遠陷入困境。 （雖然我對此表示懷疑。） **數字和函數之后會出現什么？** 微積分的典型課程包括以下主題： 1.如何找到各種函數的瞬時變化（稱為“導數”）。 （這樣做的過程稱為**“分化”**。） 2.如何使用導數來解決各種問題。 3.如何從函數的導數返回到函數本身。 （此過程稱為**“積分”**。） 4.研究積分某些函數的詳細方法。 5.如何使用積分來解決各種幾何問題，例如某些區域的面積和體積的計算。 在這樣的課程中還有一些其他標準主題。這些包括功率系列函數的描述，以及無限級數何時“收斂”到數字的研究。 **那么這又能讓我做什么呢？** 它并沒有真正這樣做。問題在于這些課程最初是在幾個世紀前設計的，它們的目的不是賦予權力（當時完全不可能），而是讓觀眾熟悉能夠理解更高級工作的想法和概念以及符號。數學家，科學家和工程師在各種情境中使用微積分概念，并使用行話和符號，在沒有學習微積分的情況下，對你來說是完全不可理解的。對微積分的研究通常旨在為您提供與這種更高級工作相關的“數學復雜性”。 **為什么這個關于賦權的廢話呢？** 本課程將嘗試與眾不同，旨在賦予權力以及其他通常的目標。它可能不會成功，但至少會嘗試。 **它將如何嘗試執行這個奇跡？** 傳統的微積分課程強調用于進行微分和積分的代數方法。我們將描述這些方法，但也展示了如何在計算機電子表格上進行微分和積分（以及常微分方程的解法），并且需要付出額外的努力。我們還將提供小程序自動執行相同操作的小程序。使用這些小程序或電子表格，您可以比以前更輕松，更靈活地應用微積分工具。 （還有更多高級程序，例如 MAPLE 和 Mathematica，它們可以讓您以類似的方式輕松完成。通過它們，您可以在各種環境中推斷出各種模型的后果。一旦理解了微積分可以使它的使用變得更加容易，但它們提供了輸入的答案，而這些答案并不能理解它們是如何做到的。） 此外，我們將更加重視建模系統。通過建模和解決它們導致的微分方程的方法，您可以實現我們所宣稱的賦權。 **我能用這個值得結束嗎？** 好吧，可能不是。但你可能會。此外，您可能會被激怒以了解有關您想要學習的系統或數學的更多信息，以提高您這樣做的機會。此外，您可能能夠比現在更好地理解模型的可能后果。您也可以喜歡微積分的概念和想法。 **嗯，關于數字的介紹章節是什么？** 我們從自然數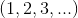開始，并注意減法，除法和取平方根的操作如何引導我們擴展我們的數字系統以包括負數，分數（稱為有理數）和復數。我們還描述了十進制擴展（描述“實數”）并檢查可數性的概念。我們也會對復數進行嘀咕。 **在關于函數的章節中？** 我們從函數的抽象定義（作為一組參數 - 值對）開始，然后描述標準函數。這些是通過以身份函數（value = argument）和指數函數開始并對它們使用各種操作而獲得的那些。 **運營，什么運營？** 這些是加法，減法，乘法，除法，替換和反演。 **但是什么是指數函數，什么是替換和反轉？** 這里有一句話答案：如果你想了解更多閱讀本章！ 指數函數是使用微積分神秘定義的：它是函數，它是自己的導數，定義為在參數 0 處具有值 1.然而，事實證明，這是你以前見過的東西。事實證明它與三角函數的正弦函數有著密切的關系。 **將一個函數 f 替換為另一個函數 f** 會產生一個新函數，該函數定義為在參數 x 處具有參數 f 的值 f，該參數是參數 x 處的 g 的值。這比聽起來簡單。假設，例如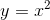和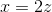，則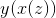是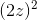。 **函數的反函數**是通過用其參數切換其值而獲得的函數。例如，通常寫為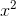的平方函數具有平方根函數作為反函數。 在威廉神父對他的侄子的不朽言論中，由數學家劉易斯卡羅爾寫道： 我已回答了三個問題，這就夠了， 圣人說，不要給自己吹氣。 你覺得我可以整天聽這些東西嗎？ 關閉或者我會把你踢到樓下！