# 1.2 小數和實數
> 原文: [http://math.mit.edu/~djk/calculus_beginners/chapter01/section02.html](http://math.mit.edu/~djk/calculus_beginners/chapter01/section02.html)
我們有一種很好的方式來表示包括分數在內的數字,這就是十進制擴展。假設我們考慮的數字如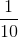,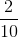,(與相同),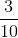等等。
我們把它們寫成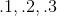,依此類推。小數點是一個代碼,告訴我們超出它的數字除以 10。
我們可以通過在小數點后添加第二個數字將其擴展為除以 100 的整數。因此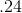表示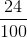。我們可以繼續保持正確的狀態,用小數點后的較長和較長的整數串來描述整數除以千或百萬等等。
但是,如果我們停下來,我們就不會以這種方式得到所有有理數我們只會得到分數為十的冪的有理數。像 1/3 這樣的數字將成為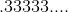,三分球將永遠存在。 (這通常被寫為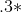,這個星形表示它前面的東西是無休止地重復)
為了使用這種十進制表示法得到所有有理數,你必須愿意永遠繼續下去。如果你這樣做,你會得到比有理數更多的東西。以小數點開頭的所有數字序列的集合為您提供 0 到 1 之間的所有有理數,甚至更多。你得到的被稱為**實數**在 0 和 1 之間。有理數的結果是無窮無盡的,如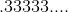,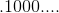,或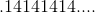,(又名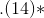 ])。
現在你和我以及任何計算機都沒有真正繼續寫下一個數字,所以對于這個實數的概念存在一種不真實的感覺,但那又是什么呢?在你的想象中,你可以直觀地看到一連串的數字。這將代表一個實數。
如果在有限位數后停止實數,則會得到一個有理數(因為在停止之后的所有條目都是零)。因此,對有理數起作用的加法,減法,乘法和除法的規則也可用于對實數進行相同的處理。幸運的是,當數字非常接近小數點的非零數字時,數字中小數點右側的數字對計算幾乎沒有影響。
既然我們不能在現實生活中繼續描述一個非理性的實數,那么我們必須以其他方式描述它。以下是描述數字的不同方式的示例。
我們定義了具有十進制擴展的數字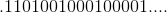;在**每個連續的對之間,有一些比前一個連續的 1 對更多。** 這個數字不合理;它不會重演。
我們不必,但只是為了它的樂趣,我們將更進一步,再次擴展我們的數字,復雜的數字。如果要定義一個數字平方操作的反轉,則需要這樣做。 (復數是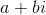形式的實體,其中和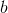是實數,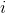平方是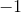。)
- 第 0 章:為何學習微積分?
- 0.1 你應該知道什么
- 0.2 什么是微積分?我們為什么要研究它?
- 第 1 章:數字
- 1.1 什么是數字?有理數
- 1.2 小數和實數
- 1.3 復數
- 復數運算
- 1.4 可數集(消遣)
- 第 2 章:使用電子表格
- 2.1 什么是電子表格?
- 2.2 斐波納契數
- 2.3 帕斯卡的三角形
- 2.4 與電子表格集成
- 第 3 章:線性函數
- 3.1 什么是函數?
- 3.2 線性函數
- 3.3 線性
- 第四章:函數的二次型和導數
- 4.1 更復雜的函數
- 4.2 二次函數的斜率
- 第 5 章:有理函數和導數的計算
- 5.1 有理函數的導數
- 第 6 章:指數函數,替換和鏈規則
- 6.1 最有用函數的導數
- 第 7 章:三角函數及其導數
- 7.1 二維數學
- 7.2 三角學和導數以及加法定理
- 第 8 章:反函數及其導函數
- 8.1 反函數
- 8.2 微分反函數
- 8.3 更多規則
- 第 9 章:數值微分和不可微函數
- 9.1 數值微分
- 9.2 繪制導數圖
- 9.3 不可微函數
- 第 10 章:微分的回顧
- 10.1 復習
- 第 11 章:微分在求解方程中的應用
- 11.1 求解方程
- 第 12 章:反導數
- 12.1 反導數
- 第 13 章:曲線下面積;定積分
- 13.1 區域:定義,名稱和符號
- 13.2 微積分和確定區域的基本定理
- 13.3 積分的訣竅
- 第 14 章:數值積分
- 14.1 數值積分計劃
- 14.2 積分的“規則”
- 14.3 為什么這些規則有效?
- 第 15 章:平行數字的面積和體積;行列式
- 15.1 有符號面積和體積
- 15.2 表示平行邊的圖形
- 15.3 行列式的屬性
- 15.4 求解行列式
- 15.5 用于求解電子表格中的行列式的愛麗絲夢游仙境方法
- 第 16 章一些純數學
- 16.1 極限和點集拓撲簡介
- 16.2 緊集
- 16.3 雜注
- 16.4 Lebesgue 積分
- 第 17 章:物理的建模應用
- 17.1 垂直運動建模
- 17.2 彈簧建模(諧波振蕩器)
- 17.3 受迫振蕩
- 17.4 簡單電路
- 第 18 章捕食者獵物模型
- 18.1 捕食者獵物模型
- 第 19 章:求解微分方程
- 19.1 計劃
- 19.2 一階微分方程
- 19.3 二階微分方程
- 19.4 行星運動
