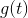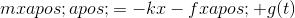
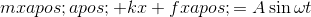
# 17.3 受迫振蕩 > 原文： [http://math.mit.edu/~djk/calculus_beginners/chapter17/section03.html](http://math.mit.edu/~djk/calculus_beginners/chapter17/section03.html) 當彈簧上的物體受到外力時，即某種函數，，我們一直在考慮的模型  強迫可以是任何形式。我們通過查看對任何給定頻率的正弦強制響應來處理。我們這樣做的原因有三個。 首先，我們可以求解得到的方程，并且解決方案具有本身有趣的屬性。 其次，在許多其他環境中出現了相同的方程，例如在電路的研究中，這些特性非常重要。 第三，解決方案可用于解決一般問題。任何刺激都可以寫成正弦函數的和或積分，然后這些解可以用來獲得描述解的相應和或積分。 然后我們的模型由等式描述  給定這個方程的任何解，我們可以用作為右邊的術語來添加任何方程式，我們仍然會有一個解決方案。正如我們在上一節中看到的那樣，只要非零，這種解決方案就會在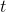中呈指數衰減。由于這種衰減，“均勻”方程（右側為零）的解被稱為瞬態解。因此，我們將注意力集中在穩態解決方案上，這種解決方案會持續存在，因為強制函數仍然存在。 這些解決方案將具有與強制函數相同的頻率和周期性，因此我們查看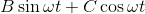形式的解決方案。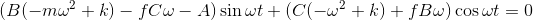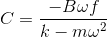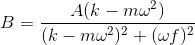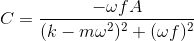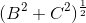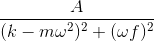我們發現  從這些我們推斷出這里的兩個系數都必須消失，這告訴我們：  和  導致  and  對強迫的響應幅度為而變為  非強制和無阻尼彈簧具有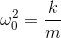給出的“固有頻率”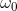。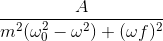剛才描述的幅度可以用ω <sub>0</sub> 表示為  當與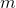相比相當小時，該反應表現出稱為**共振**的現象。也就是說，當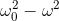非常小，并且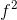與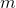相比較小時，分母變得非常小并且響應變得非常大。