# 6.1 最有用函數的導數
> 原文: [http://math.mit.edu/~djk/calculus_beginners/chapter06/section01.html](http://math.mit.edu/~djk/calculus_beginners/chapter06/section01.html)
Rational 函數是一個重要且有用的函數類,但還有其他函數。我們實際上通過從身份函數之外的兩個附加函數開始獲得最有用的函數,并且除了加法減法乘法和除法之外還允許兩個以上的操作。
**還有什么額外的啟動函數?**
這兩個是**指數函數,**我們將暫時寫為 **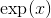,**和**正弦函數,**通常寫為 **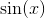。**
**這些是什么?**
我們將花費一些時間和精力來盡快介紹和描述這兩個函數及其眾多精彩屬性。目前,我們關心的只是它們存在,你可以在電子表格和科學計算器上找到它們,我們可以對它們進行算術運算(加法,減法,乘法和除法)。如果你只需要一個提示,正弦函數是角度研究的基本函數,稱為三角學。 **指數函數**根據導數定義。 **它是在參數 0 處的值為 1 的函數,它具有與其自身相同的導數。** 我們有

這個定義可能會使函數起初有點神秘,但你必須承認它可以很容易地區分這個函數。
**這個指數函數有一個重要而有趣的特性:即**
**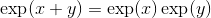**
_**(證明的想法)作為的函數,通過以下關于替換導數的陳述,我們可以推斷出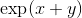的導數本身。它在的值是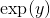。該導數與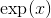的區別僅在于為時的值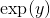而不是。這意味著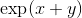的導數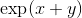本身是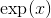乘以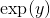。我們忽略了對的任何可能依賴性。這樣做只意味著我們正在計算所謂的“關于變量 x 的偏導數,保持變量 y 固定”。別擔心;當有多個變量時,它是我們處理微積分的??方法之一)**_
**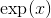的定義屬性允許我們推導出它的冪級數表示。 ** 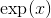具有常數項,并且作為其自身的導數必須具有線性項,其導數是,即。同樣,它必須有一個二次項,其導數為,即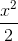。繼續這種演繹永遠給了我們
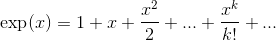
**還有哪些額外的操作?**
我們想要使用的兩個新操作是**替換,**和**反轉。**
**And what are these?**
如果我們有兩個函數,和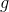,參數的值為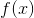和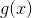,我們可以構造一個新函數,我們寫為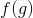,由**得到]在參數中取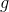的值,作為的參數。**
**** 的值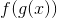,我們寫為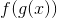,是的值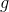的值的值;它是 **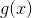在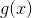中的值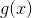。** 我們稱這個新函數**將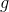替換為。** 我們將在第 8 章中進行反演。
替換比聽起來更簡單。假設您在框 A5 中的電子表格中有的值,并且您在框 B5 中放置= g(A5),在 C5 中放置= f(B5)。那么 C5 將包含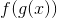。
如果將多項式替換為多項式,則只需得到多項式,如果將有理函數替換為有理函數,則仍然具有有理函數。但如果你把這些東西替換成指數和正弦,你會得到全新的東西(如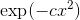),這是概率論的基本函數。
正如利用指數函數或正弦函數的復制品對電子表格或科學計算器沒有任何問題一樣,替換也沒有真正的問題。我們已經看到你可以在 B10 中創建 g(A10),然后在 C(10)中創建 f(B10)并且在 C10 中創建了替換值 f(g(A10))。你可以通過重復這個過程,構建最可怕的替換組合和可想象的算術運算,甚至比你想象的還要糟糕,只有很少的難度,你也可以找到它們的數值導數。
在我們繼續上一次操作之前,我們注意到有一個與替換操作相關的很好的屬性。正如我們已經找到上面的公式來找到總和或乘積的導數或者我們知道的導數的函數的比率,我們**根據其成分的導數得到了替代函數的導數的整齊公式。** 實際上它可以是一個簡單的公式。
結果通常稱為**鏈規則:**
某些自變量的的導數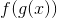與任何其他導數一樣,是在函數處與該函數相切的直線的斜率。與所有斜率一樣,該斜率是給定函數的變化與其參數變化的比率,在非常接近參數的任何區間。因此,的導數是的微小變化除以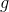的變化。替換將分母改為中的微小變化。
假設,我們對變量做了一個非常小的變化,非常接近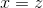,這個變化足夠小,以至于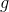和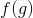的線性近似在變化的區間內非常準確。讓我們稱之為改變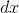。這將引起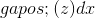的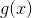的變化,(因為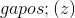的定義是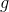的變化與的變化非常接近的比率。 )
如果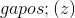為 0,那么當取決于時,g 不會改變,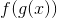也不會改變,因為它的參數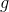取決于。 (如果 f 對具有其他依賴性,那么從其他依賴性對其導數的貢獻會增加來自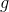變化的貢獻,并且在這里無關緊要。)
如果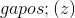不是,我們可以將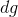定義為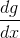,并使用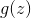中的參數的變化由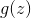給出的事實
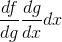,其中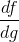在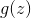評估,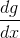在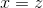評估。
根據這一說法,鏈條規則可以讀取
**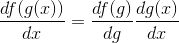**
換句話說,這意味著取代函數的**導數值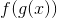,相對于變量是組成函數和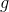的導數的乘積,取自相關論點:本身為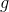,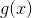為。**
**一些例子怎么樣?**
我們將給出兩個例子,但你應該為自己制定至少十幾個例子。
**例 1:假設我們將具有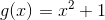給出的值的函數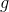替換為取值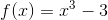的函數。**
替代函數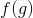具有值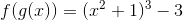。
讓我們計算這個函數的導數。 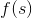相對于的導數是 **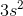,**,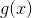相對于的導數是 **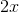。**
如果我們設置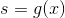 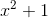,并取這兩個產品,我們得到:
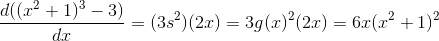
你可以在這里將多維數據集相乘,然后進行區分以獲得相同的結果,但這樣做會更加混亂,并且大多數人在執行此操作時至少會犯一個錯誤。如果按照連鎖規則進行,那么即使是第一次,你也有可能把這些事情做好。 (不幸的是,如果你正確地執行它,你將無法從中進行任何練習調試。)
**例 2:找到函數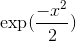的導數。**
這是通過將函數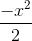代入指數函數而獲得的函數。
函數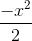的導數是函數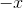;指數函數是它自己的導數。
在應用鏈規則時,我們發現: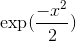的導數是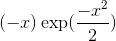,后一因子是在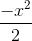評估的指數函數的導數。
**練習:**
**6.1 寫下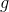代入的結果的表達式,形成下列函數對的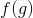,并使用鏈規則找到它們的導數的表達式。**
**a。由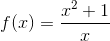定義的,由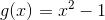定義的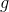。**
**b。 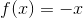由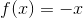定義,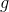由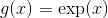定義。**
**c。 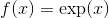由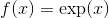定義,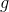由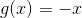定義。**
**6\. 2 使用[衍生小程序](../chapter04/section02.html#DerivativeTangentLine)檢查每個結果。**
**6.3**
**a。考慮公式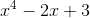定義的函數。使用小程序繪制它并查看其導數。它的最小值在哪里,它是什么?它在最小點的導數是什么?從 applet 估計這些東西。**
**b。找到的最大點和該參數的的值近似為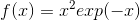,**定義的
**c。如果函數在從到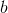的區間內是可微分的并且在和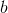之間的點處具有最小值,那么它在處的導數是什么?**
**6.4 使用鏈規則顯示: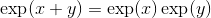。**
**好的,我現在在哪里?**
此時,您可以使用規則來區分使用算術運算和以身份函數(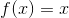開頭)或神秘指數函數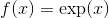開頭的替換所能完成的所有函數。
**在下一節中,我們將擴展內容,以便您可以從正弦函數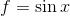開始,并區分您可以創建的任何內容。最后,我們將擴展規則以區分反函數。**
**這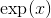是什么?**
數字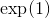稱為。性質: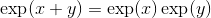暗示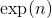是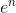,因為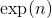是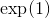 倍的產物。當不是整數時,我們還沒有定義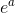。當我們確定它時,我們會發現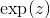對于所有實數或復數都是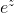。實際上,我們將明確定義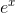的的合理值,并顯示它是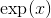和**然后將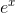定義為無理值為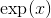。**
**什么是?**
回答這個問題的一個簡單方法是將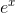寫為的冪和乘以適當的系數,然后設置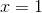。我們可以通過要求其導數是前一項來計算總和中每個冪的系數。
因此,根據定義,我們知道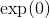,總和中的常數項是 1.對于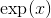是它自己的導數,它必須包含其導數是這個常數項的東西,。導數為的術語是;導數為的術語是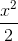;其導數為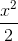的術語是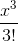,其中是乘以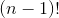。而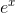總和中的一般術語是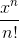。 (我們已經證明了這一點,但我非常喜歡它,我正在重復它。)
這告訴我們是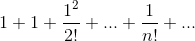
**練習 6.5 使用電子表格**對本系列的前 18 個術語求和。
我得到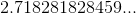的數字。事實證明,不是理性的,甚至不是多項式方程的解。這些數字被稱為**超驗。**
**當不是整數時,如何定義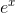?**
**當合理時,說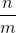,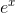是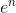的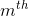根。否則它由上面證明的無窮大功率系列定義:**
**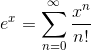**
- 第 0 章:為何學習微積分?
- 0.1 你應該知道什么
- 0.2 什么是微積分?我們為什么要研究它?
- 第 1 章:數字
- 1.1 什么是數字?有理數
- 1.2 小數和實數
- 1.3 復數
- 復數運算
- 1.4 可數集(消遣)
- 第 2 章:使用電子表格
- 2.1 什么是電子表格?
- 2.2 斐波納契數
- 2.3 帕斯卡的三角形
- 2.4 與電子表格集成
- 第 3 章:線性函數
- 3.1 什么是函數?
- 3.2 線性函數
- 3.3 線性
- 第四章:函數的二次型和導數
- 4.1 更復雜的函數
- 4.2 二次函數的斜率
- 第 5 章:有理函數和導數的計算
- 5.1 有理函數的導數
- 第 6 章:指數函數,替換和鏈規則
- 6.1 最有用函數的導數
- 第 7 章:三角函數及其導數
- 7.1 二維數學
- 7.2 三角學和導數以及加法定理
- 第 8 章:反函數及其導函數
- 8.1 反函數
- 8.2 微分反函數
- 8.3 更多規則
- 第 9 章:數值微分和不可微函數
- 9.1 數值微分
- 9.2 繪制導數圖
- 9.3 不可微函數
- 第 10 章:微分的回顧
- 10.1 復習
- 第 11 章:微分在求解方程中的應用
- 11.1 求解方程
- 第 12 章:反導數
- 12.1 反導數
- 第 13 章:曲線下面積;定積分
- 13.1 區域:定義,名稱和符號
- 13.2 微積分和確定區域的基本定理
- 13.3 積分的訣竅
- 第 14 章:數值積分
- 14.1 數值積分計劃
- 14.2 積分的“規則”
- 14.3 為什么這些規則有效?
- 第 15 章:平行數字的面積和體積;行列式
- 15.1 有符號面積和體積
- 15.2 表示平行邊的圖形
- 15.3 行列式的屬性
- 15.4 求解行列式
- 15.5 用于求解電子表格中的行列式的愛麗絲夢游仙境方法
- 第 16 章一些純數學
- 16.1 極限和點集拓撲簡介
- 16.2 緊集
- 16.3 雜注
- 16.4 Lebesgue 積分
- 第 17 章:物理的建模應用
- 17.1 垂直運動建模
- 17.2 彈簧建模(諧波振蕩器)
- 17.3 受迫振蕩
- 17.4 簡單電路
- 第 18 章捕食者獵物模型
- 18.1 捕食者獵物模型
- 第 19 章:求解微分方程
- 19.1 計劃
- 19.2 一階微分方程
- 19.3 二階微分方程
- 19.4 行星運動
