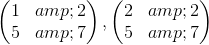
# 15.4 求解行列式 > 原文： [http://math.mit.edu/~djk/calculus_beginners/chapter15/section04.html](http://math.mit.edu/~djk/calculus_beginners/chapter15/section04.html) 那么，從前兩個事實來看，我們可以計算任何行列式的值，從而計算任何平行邊圖的面積或體積或任何值。 **怎么樣？** 好吧，我們可以將多個行相加，以擺脫對角線元素。當我們完成時，我們可以推斷出行列式的值是對角元素的乘積。 實際上，我們只需要將對角線一側的元素設為，并取對角線元素的乘積。擺脫其他人有時是一件好事，但根本不會影響對角元素。 讓我們評估以下數組的行列式：  如果我們從第一個矩陣中的第二行中減去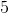乘以第一行，我們得到第二行的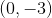，因此行列式為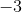。在第二個數組中，我們從第二個數組中減去乘以第一行，并將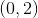作為新的第二行。因此，第二基質的行列式是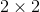或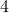。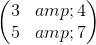 這通過線性告訴我們這兩個矩陣之和的行列式，  是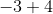或。我們可以通過從第二行中減去第一行的來驗證這一點，將第二行轉換為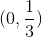，并且對角元素的乘積是。當兩個數組具有相同的基數時，您可以以這種方式應用行列式的線性，并且僅在非基數行中不同。 用于評估兩個矩陣上使用的行列式（有時稱為“行減少”，有時稱為“高斯消除”）的這個過程可以應用于任何大小的正方形陣列。 陣列很容易為做，但即使這樣也很容易出錯。對于而言仍然相當容易，但是大多數人會在這個過程中犯下一些愚蠢的錯誤，因為這樣做的步驟太無聊了，而且大部分時間都會出錯。即使你和我可以期望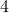行列式在大多數情況下通過這種方法手動完成時也會錯誤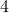，因為這些步驟非常簡單且無趣。你的思想會一路走來，你很有可能搞砸了。 **這是評估行列式的唯一方法嗎？** 不，至少還有其他兩種方式，其中一種方式同樣無聊，容易出錯。另一個是神奇而有趣的，但令人驚訝的是它從未被教過，很少有人聽說過它。 一種標準方法是為剛剛描述的方法的結果編寫公式。如果從行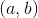和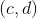開始。要將轉換為，請從第二行減去的第一行。得到的對角元素是和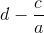，它們的產物是 **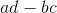** 。這是一般二乘二陣列的行列式的公式。計算三乘三個行列式的標準方法是在三個向下傾斜的對角線上取條目的乘積，并從它們的總和中減去三個向上傾斜的對角線中的每一個上的條目乘積的總和。 **練習 15.6 通過上述任何方法評估以下行列式。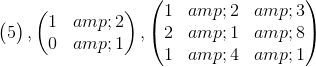**  **那么神奇的方法是什么？**