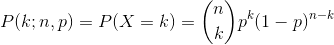
## 3.3 概率分布 我們通常希望能夠量化實驗中任何可能值的概率。例如，在 2018 年 1 月 20 日，籃球運動員斯蒂芬·科里在與休斯頓火箭隊的比賽中 4 次罰球中只有 2 次命中。我們知道庫里在整個賽季的罰球命中率是 0.91，所以他在一場比賽中只命中 50%的罰球似乎是不太可能的，但這到底有多不可能呢？我們可以使用理論概率分布來確定這一點；在本課程中，我們將遇到許多這樣的概率分布，每個概率分布都適合描述不同類型的數據。在這種情況下，我們使用 _ 二項式 _ 分布，它提供了一種方法來計算在給定一些已知的成功概率的情況下，許多“伯努利試驗”（即，成功或失敗的試驗，兩者之間沒有任何結果）中一些成功的概率。每次審判。此分布定義為：  這是指成功概率為 p 時 n 次試驗中 k 次成功的概率。您可能不熟悉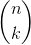，這被稱為 _ 二項式系數 _。二項式系數也被稱為“n-choose-k”，因為它描述了從 n 個項目中選擇 k 個項目的不同方法的數量。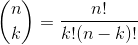二項式系數計算如下：  解釋點在哪里！！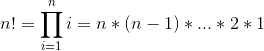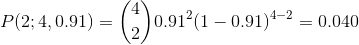）指數字的 _ 階乘 _：  以斯蒂芬·庫里的罰球為例：  這表明，考慮到庫里的總罰球率，他不太可能在 4 次罰球中只命中 2 次。這只是為了表明不太可能的事情實際上發生在現實世界中。 ### 3.3.1 累積概率分布 通常我們不僅想知道某個特定值的可能性有多大，而且想知道找到一個和某個特定值一樣極端或更極端的值的可能性有多大。為了回答這個問題，我們可以使用 _ 累積 _ 概率分布；而標準概率分布告訴我們某個特定值的概率，而累積分布告訴我們一個值比它大或大（或小或小）的概率。Me 特定值。 在罰球的例子中，我們可能想知道：如果斯蒂芬·庫里的罰球概率為 0.91，那么他在四個罰球中命中 2 個（htg0）或更少（htg1）的概率是多少。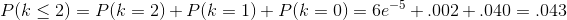為了確定這一點，我們可以簡單地使用二項式概率方程并插入 k 的所有可能值：  在許多情況下，可能的結果數量對于我們來說太大，無法通過列舉所有可能的值來計算累積概率；幸運的是，它可以直接計算。對于二項式，我們可以使用`pbinom()`函數在 r 中執行此操作： ```r # compute cumulative probability distribution for Curry's free throws tibble( numSuccesses = seq(0, 4) ) %>% mutate( probability = pbinom(numSuccesses, size = 4, prob = 0.91) ) %>% pander() ``` <colgroup><col style="width: 20%"> <col style="width: 20%"></colgroup> | 無數次成功 | 可能性 | | --- | --- | | 0 | 0 | | 1 個 | 0.003 個 | | 二 | 0.043 個 | | 三 | 0.314 個 | | 4 | 1 | 由此我們可以看出咖喱在 4 次嘗試中 2 次或更少的罰球機會是 0.043。