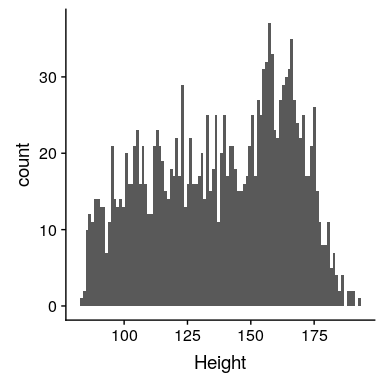
## 5.2 統計建模：示例 讓我們來看一個使用 nhanes 中的數據將模型擬合到數據的示例。特別是，我們將嘗試在 nhanes 樣本中建立兒童身高的模型。首先，讓我們加載數據并繪制它們（參見圖[5.1](#fig:childHeight)）。  圖 5.1 NHANES 兒童身高柱狀圖。 請記住，我們希望盡可能簡單地描述數據，同時仍然捕獲它們的重要特性。我們能想象的最簡單的模型是什么，它仍然能夠捕獲數據的本質？數據集中最常見的值（我們稱之為 _ 模式 _）如何？R 沒有內置的模式函數，所以我們將首先創建一個，我們稱之為`getmode()`。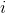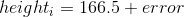 ```r # create function to compute mode and apply to child height data from NHANES getmode <- function(v) { uniqv <- unique(v) return(uniqv[which.max(tabulate(match(v, uniqv)))]) } height_mode <- getmode(NHANES_child$Height) paste("mode of children's height from NHANES:", height_mode) ``` ```r ## [1] "mode of children's height from NHANES: 166.5" ``` 鑒于此，我們針對單個數據點的模型將是：  這就用一個數字重新定義了 1691 個孩子的整個集合，如果我們想預測任何一個新孩子的身高，那么我們的猜測將是相同的數字：166.5 厘米。 這個模型有多好？一般來說，我們用誤差來定義模型的優度，它代表了模型和數據之間的差異；所有事物都是相等的，產生較低誤差的模型就是更好的模型。 ```r # compute error compared to the mode and plot histogram error_mode <- NHANES_child$Height - height_mode sprintf("average error from mode (cm): %0.2f", mean(error_mode)) ``` ```r ## [1] "average error from mode (cm): -28.80" ``` 我們發現平均個體的誤差相當大，為-28.8 厘米。我們想要一個平均誤差為零的模型，結果是如果我們使用算術平均值（通常稱為 _ 平均值 _）作為我們的模型，那么情況就是這樣。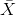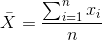 平均值（通常用變量上的條表示，如）定義為：  也就是說，它是所有值的總和，除以值的數目。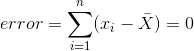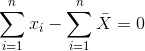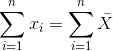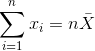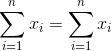我們可以證明平均誤差（因此平均誤差）之和為零：      考慮到平均誤差為零，這似乎是一個更好的模型。讓我們確認一下它是正確的。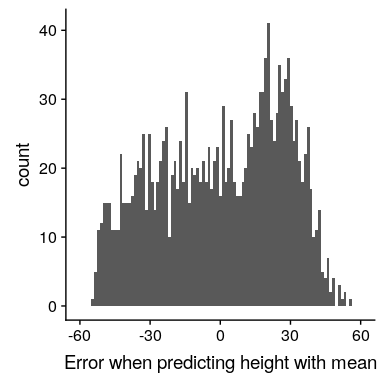 ```r # compute error from mean error_mean <- NHANES_child$Height - mean(NHANES_child$Height) sprintf("average error for mean (cm): %e", mean(error_mean)) ``` ```r ## [1] "average error for mean (cm): -9.864171e-15" ```  圖 5.2 平均值誤差分布。 這里的平均誤差是一個非常小的數字，雖然技術上不是零；我們稍后將在課程中討論為什么會發生這種情況（這是由于計算機如何表示數字），但現在您可以將其視為接近零，稱之為零。 盡管平均誤差的平均值為零，但從圖[5.2](#fig:meanError)中的柱狀圖可以看出，每個個體仍然存在一定程度的誤差；有些是正的，有些是負的，而這些誤差相互抵消。出于這個原因，我們通常用某種將正錯誤和負錯誤都算作壞的度量來總結錯誤。我們可以使用每個誤差值的絕對值，但更常見的是使用平方誤差，這是我們將在本課程后面看到的原因。 有幾種常見的方法來總結在本書的不同點上會遇到的平方誤差，因此了解它們之間的關系是很重要的。首先，我們可以簡單地把它們加起來；這被稱為 _ 平方誤差之和 _。我們通常不使用它的原因是它的大小取決于數據點的數量，所以除非我們觀察相同數量的觀測結果，否則很難解釋。其次，我們可以取平方誤差值的平均值，即 _ 平均平方誤差（mse）_。但是，由于我們在求平均值之前對這些值進行了平方處理，因此它們與原始數據的比例不同；它們位于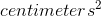中。由于這個原因，我們也經常采用 mse 的平方根，我們稱之為 _ 均方根誤差（rmse）_，因此它與原始值的單位相同（在本例中為厘米）。 ```r # compute and print RMSE for mean and mode rmse_mean <- sqrt(mean(error_mean**2)) rmse_mode <- sqrt(mean(error_mode**2)) print(paste("Mode: root mean squared error (centimeters):", rmse_mode)) ``` ```r ## [1] "Mode: root mean squared error (centimeters): 39.4197926582947" ``` ```r print(paste("Mean: root mean squared error (centimeters):", rmse_mean)) ``` ```r ## [1] "Mean: root mean squared error (centimeters): 26.9116738708646" ``` 這表明平均值有相當大的誤差——任何數據點平均距離平均值大約 27 厘米——但它仍然比模式好得多。 ### 5.2.1 改進我們的模型 我們能想象一個更好的模型嗎？請記住，這些數據來自 NHANES 樣本中的所有兒童，他們的年齡從 2 歲到 17 歲不等。鑒于年齡范圍很廣，我們可能期望我們的身高模型也包括年齡。讓我們繪制身高和年齡的數據，看看這種關系是否真的存在。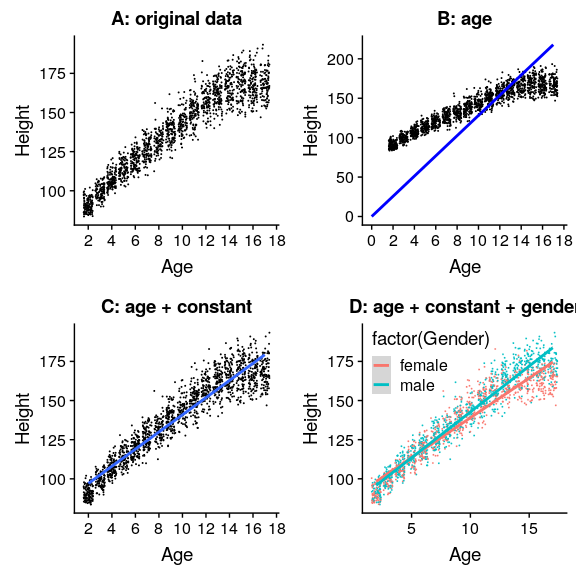  圖 5.3 NHANES 兒童的身高，未使用模型（a）繪制，線性模型僅包括年齡（b）或年齡和常數（c），線性模型適合男性和女性年齡的單獨影響（d）。 圖[5.3](#fig:childHeightLine)的面板 A 中的黑點顯示了數據集中的個體，正如我們所期望的，身高和年齡之間似乎有著很強的關系。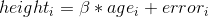因此，我們可以建立一個高度與年齡相關的模型：  其中是一個 _ 參數 _，我們用年齡相乘得到最小的誤差。您可能已經注意到，這只是一條斜率為的直線，為了看到這一點，讓我們在數據頂部用藍色繪制出最適合的直線（圖[5.3](#fig:childHeightLine)中的面板 B）。這個模型顯然有問題，因為這條線似乎沒有很好地跟蹤數據。事實上，這個模型（39.16）的 RMSE 實際上比只包含平均值的模型高！這個問題是因為我們的模型只包括年齡，這意味著當年齡為零時，模型的高度預測值必須為零。即使數據不包括任何年齡為零的子代，但當 x 為零時，該行在數學上被限制為 Y 值為零，這就解釋了為什么該行被下拉到較年輕的數據點之下。我們可以通過在我們的模型中包含一個常量來解決這個問題，它基本上代表年齡等于零時高度的估計值；盡管在這個數據集中零歲的年齡是不合理的，但這是一個數學技巧，它將允許模型解釋數據。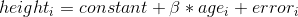模型為：  其中 _ 常數 _ 是對所有個體的預測增加的一個常量值（我們也稱為 _ 截距 _，因為它映射到一條直線方程中的截距上）。稍后我們還將了解如何實際計算這些值；現在，我們將使用 r 中的`lm()`函數計算常量的值，并使用計算出最小的錯誤。圖[5.3](#fig:childHeightLine)中的面板 C 顯示了適合于 nhanes 數據的該模型，在該模型中，我們看到線條與數據的匹配比沒有常量的要好得多。 ```r ## [1] "model: height = 86.11 + 5.48*Age" ``` ```r ## [1] "root mean squared error: 8.36" ``` 使用這個模型，我們的誤差要小得多——平均只有 8.36 厘米。你能想到其他可能與身高有關的變量嗎？性別呢？在圖[5.3](#fig:childHeightLine)的面板 D 中，我們用分別為男性和女性安裝的線條繪制數據。從情節上看，男性和女性之間似乎存在差異，但相對較小，僅在青春期后出現。讓我們估計一下這個模型，看看錯誤是什么樣子的： ```r # compute model fit for modeling with age and gender model_age_gender <- lm(Height ~ Age + Gender, data = NHANES_child) rmse_age_gender <- NHANES_child %>% add_predictions(model_age_gender, var = "predicted_age_gender") %>% summarise( sqrt(mean((Height - predicted_age_gender)**2)) ) %>% pull() sprintf( "model: height = %0.2f + %0.2f*Age + %0.2f*Gender", model_age_gender$coefficients[1], model_age_gender$coefficients[2], model_age_gender$coefficients[3] ) ``` ```r ## [1] "model: height = 84.37 + 5.48*Age + 3.28*Gender" ``` ```r print(sprintf("root mean squared error: %0.2f", rmse_age_gender)) ``` ```r ## [1] "root mean squared error: 8.20" ``` 在圖[5.4](#fig:msePlot)中，我們繪制了不同模型的均方根誤差值。從這一點上，我們可以看到，從一種模式到另一種模式，從一種模式到另一種模式，從一種模式到另一種模式再到另一種模式+年齡，這個模式變得更好了一點，而且只通過將性別也包括在內，就可以說更好了。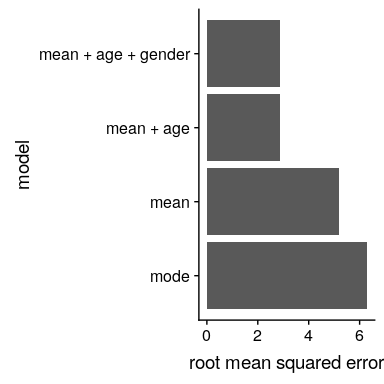  圖 5.4 為上述測試的每個模型繪制的均方誤差。