## 9.3 無效假設檢驗過程
我們可以將無效假設測試的過程分解為若干步驟:
1. 在看到數據之前,制定一個能夠體現我們預測的假設(_)_
2. 收集一些與假設相關的數據
3. 指定空假設和可選假設
4. 將模型與代表替代假設的數據相匹配,并計算檢驗統計
5. 假設零假設為真,計算該統計的觀測值的概率。
6. 評估結果的“統計顯著性”
對于實際操作示例,讓我們使用 nhanes 數據來問以下問題:體力活動是否與體重指數相關?在 NHANES 數據集中,參與者被問及他們是否經常從事中等強度或高強度的運動、健身或娛樂活動(存儲在變量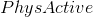中)。他們還測量了身高和體重,并計算了體重指數:
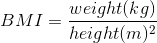
### 9.3.1 步驟 1:制定假設
對于第 1 步,我們假設不從事體育活動的人的體重指數應該比那些從事體育活動的人大。
### 9.3.2 步驟 2:收集一些數據
對于步驟 2,我們收集一些數據。在這種情況下,我們將從 nhanes 數據集中抽取 250 個人作為樣本。圖[9.1](#fig:bmiSample)顯示了這樣一個樣本的例子,其中 bmi 分別為活躍和不活躍的個體顯示。
```r
# sample 250 adults from NHANES and compute mean BMI separately for active
# and inactive individuals
sampSize <- 250
NHANES_sample <-
NHANES_adult %>%
sample_n(sampSize)
sampleSummary <-
NHANES_sample %>%
group_by(PhysActive) %>%
summarize(
N = length(BMI),
mean = mean(BMI),
sd = sd(BMI)
)
# calculate the mean difference in BMI between active
# and inactive individuals; we'll use this later to calculate the t-statistic
meanDiff <-
sampleSummary %>%
select(
PhysActive,
mean
) %>%
spread(PhysActive, mean) %>%
mutate(
meanDiff = No - Yes
) %>%
pull(meanDiff)
# calculate the summed variances in BMI for active
# and inactive individuals; we'll use this later to calculate the t-statistic
sumVariance <-
sampleSummary %>%
select(
PhysActive,
N,
sd
) %>%
gather(column, stat, N:sd) %>%
unite(temp, PhysActive, column) %>%
spread(temp, stat) %>%
mutate(
sumVariance = No_sd**2 / No_N + Yes_sd**2 / Yes_N
) %>%
pull(sumVariance)
# print sampleSummary table
pander(sampleSummary)
```
<colgroup><col style="width: 18%"> <col style="width: 8%"> <col style="width: 11%"> <col style="width: 11%"></colgroup>
| 物理激活 | N 號 | 意思是 | 標準偏差 |
| --- | --- | --- | --- |
| 不 | 135 | 30.25 天 | 第 8.2 條 |
| 是的 | 115 | 28.6 條 | 6.88 條 |
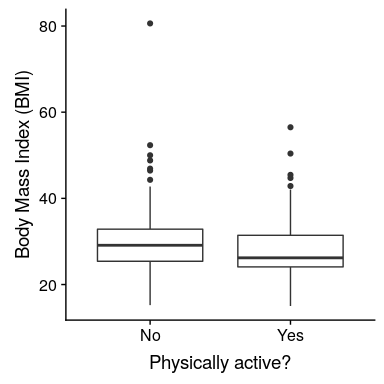
圖 9.1 NHANES 數據集成人樣本中的體重指數數據的框線圖,根據他們是否報告參與常規體育活動進行劃分。
### 9.3.3 步驟 3:指定無效假設和替代假設
對于步驟 3,我們需要指定我們的無效假設(我們稱之為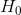)和替代假設(我們稱之為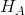)。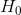是用來檢驗我們的興趣假設的基線:也就是說,如果沒有效果,我們期望數據是什么樣子的?無效假設總是涉及到某種等式(=,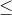或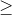)。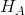描述了如果實際存在效果,我們所期望的。另一種假設總是涉及某種不等式(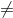、>;或<;)。重要的是,無效假設檢驗是在假設無效假設是真實的前提下進行的,除非證據另有說明。
我們還必須決定是使用 _ 定向 _ 還是 _ 非定向 _ 假設。一個非方向性的假設只是預測會有一個差異,而不預測它將朝哪個方向發展。對于 bmi/活動示例,非方向性無效假設為:
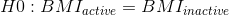
相應的非方向性替代假設是:
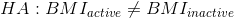
另一方面,一個方向性假設預測了差異會朝哪個方向發展。例如,我們有很強的先驗知識來預測從事體育活動的人應該比不從事體育活動的人體重輕,因此我們將提出以下定向零假設:
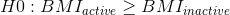
以及方向選擇:
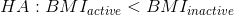
### 9.3.4 步驟 4:將模型與數據匹配,并計算測試統計
對于步驟 4,我們希望使用數據來計算一個統計,最終讓我們決定是否拒絕無效假設。為此,模型需要量化有利于替代假設的證據數量,相對于數據的可變性。因此,我們可以將測試統計看作是提供了一種與數據的可變性相比效果大小的度量。一般來說,這個檢驗統計量會有一個與之相關的概率分布,因為這允許我們確定在無效假設下觀察到的統計量值的可能性。
對于體重指數的例子,我們需要一個測試統計數據來測試兩個平均值之間的差異,因為假設是以每組的平均體重指數來陳述的。一個經常用來比較兩種方法的統計數據是 _t-statistic_,首先由統計學家 William Sealy Gossett 開發,他在都柏林的 Guiness Brewery 工作,用筆名“student”書寫,因此常被稱為“student's t-statistic”。當樣本量較小且總體標準差未知時,t 統計量適合比較兩組的平均值。兩個獨立組比較的 t 統計量計算如下:
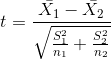
其中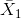和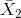是兩組的平均值,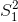和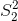是兩組的估計方差,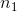和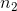是兩組的大小。t 統計量是根據概率分布(稱為 _t_ 分布)分布的。_t_ 分布看起來非常類似于正態分布,但它不同于自由度的數量,在本例中,這是觀測次數減去 2,因為我們計算了兩個平均值,因此放棄了兩個自由度。當自由度較大時(比如 1000),那么 _t_ 分布與正態分布基本相似,但當它們較小時,則 _t_ 分布的尾部比正態長(見圖[9.2](#fig:tVersusNormal))。
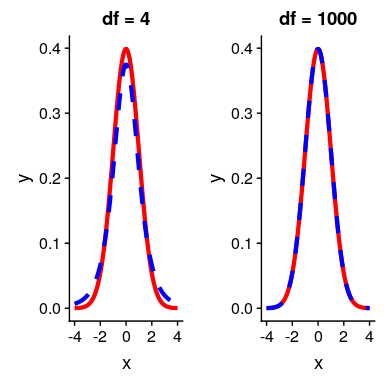
圖 9.2 各面板顯示了覆蓋在正態分布(實線紅色)上的 t 分布(藍色虛線)。左側面板顯示 4 個自由度的 t 分布,在這種情況下,分布類似,但尾部稍寬。右面板顯示了 1000 自由度的 T 分布,在這種情況下,它實際上與正常值相同。
### 9.3.5 步驟 5:確定零假設下數據的概率
這是 NHST 開始違背我們的直覺的步驟——而不是在給定數據的情況下確定虛假設為真的可能性,而是在虛假設下確定數據的可能性——因為我們從假設虛假設為真開始!要做到這一點,我們需要知道零假設下統計的概率分布,這樣我們就可以問數據在該分布下的可能性有多大。在我們轉到我們的 bmi 數據之前,讓我們從一些簡單的例子開始。
##### 9.3.5.0.1 隨機化:一個非常簡單的例子
假設我們想確定一枚硬幣是否公平。為了收集數據,我們將硬幣翻轉 100 次,并計算 70 個硬幣頭。在這個例子中,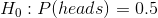和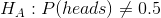,我們的測試統計只是我們計算的頭的數量。我們接下來要問的問題是:如果頭部的真實概率為 0.5,我們觀察 70 個頭部的可能性有多大。我們可以想象,這可能只是偶然發生,但似乎不太可能。為了量化這個概率,我們可以使用 _ 二項式分布 _:
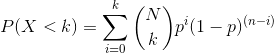
這個方程將告訴我們在給定人頭概率的情況下,一定數量人頭或更少人頭的可能性。然而,我們真正想知道的是某個或多個數字的概率,我們可以從一個數字中減去:
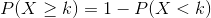
我們可以使用 r 中的`pbinom()`函數計算示例的概率,如下所示:
```r
# compute the probability of 69 or fewer heads, when P(heads)=0.5
p_lt_70 <- pbinom(69, 100, 0.5)
sprintf("probability of 69 or fewer heads given P(heads)=0.5: %0.6f", p_lt_70)
```
```r
## [1] "probability of 69 or fewer heads given P(heads)=0.5: 0.999961"
```
```r
# the probability of 70 or more heads is simply the complement of p_lt_70
p_ge_70 <- 1 - p_lt_70
sprintf("probability of 70 or more heads given P(heads)=0.5: %0.6f", p_ge_70)
```
```r
## [1] "probability of 70 or more heads given P(heads)=0.5: 0.000039"
```
這個計算表明,如果硬幣真的是公平的話,得到 70 個硬幣的可能性是非常小的。現在,如果我們沒有`pbinom()`函數來告訴我們頭部數量的概率呢?相反,我們可以通過模擬來確定它——我們使用 0.5 的真實概率反復翻轉一枚硬幣 100 次,然后計算這些模擬運行中頭部數量的分布。圖[9.3](#fig:coinFlips)顯示了該模擬的結果。
```r
# simulate tossing of 100,000 flips of 100 coins to identify empirical
# probability of 70 or more heads out of 100 flips
# create function to toss coins
tossCoins <- function() {
flips <- runif(100) > 0.5
return(sum(flips))
}
# use a large number of replications since this is fast
coinFlips <- replicate(100000, tossCoins())
p_ge_70_sim <- mean(coinFlips >= 70)
sprintf(
"empirical probability of 70 or more heads given P(heads)=0.5: %0.6f",
p_ge_70_sim
)
```
```r
## [1] "empirical probability of 70 or more heads given P(heads)=0.5: 0.000020"
```
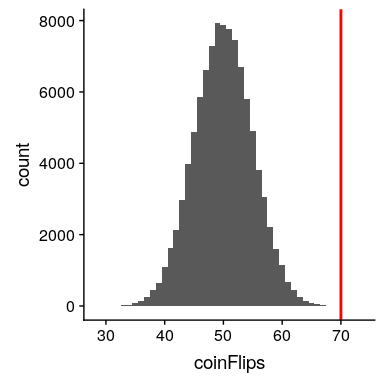
圖 9.3 100000 次模擬運行中頭數(100 次翻轉中)的分布。
在這里,我們可以看到通過模擬計算的概率(0.000020)非常接近理論概率(.00004)。
讓我們為我們的 bmi 示例進行類似的計算。首先,我們使用上面計算的樣本值計算 t 統計量:
```r
tStat <-
meanDiff / sqrt(sumVariance)
sprintf("t statistic = %0.3f", tStat)
```
```r
## [1] "t statistic = 1.735"
```
我們接下來要問的問題是:如果兩組之間的真正差異為零或更小(即方向性零假設),我們找到這種大小的 t 統計量的可能性有多大?
我們可以使用 t 分布來確定這個概率。我們的樣本量是 250,所以適當的 t 分布有 248 個自由度。我們可以使用 r 中的`pt()`函數來確定發現 t 統計量值大于或等于觀察值的概率。注意,我們想要知道一個大于我們觀察到的值的概率,但是默認情況下`pt()`給我們一個小于我們提供的值的概率,所以我們必須明確告訴它給我們“上尾”概率(通過設置`lower.tail = FALSE`)。
```r
pvalue_tdist <-
pt(tStat, df = 248, lower.tail = FALSE)
sprintf("p(t > %0.2f, df = 248) = %0.3f", tStat, pvalue_tdist)
```
```r
## [1] "p(t > 1.74, df = 248) = 0.042"
```
這告訴我們,如果虛假設真的是真的,我們觀察到的 t 統計量值 1.74 是相對不可能的。
在本例中,我們使用了一個方向性假設,因此我們只需要查看零分布的一端。如果我們想測試一個非方向性假設,那么我們就需要能夠識別出不管它的方向如何,效果的大小是多么的出乎意料。在 t 檢驗的上下文中,這意味著我們需要知道統計數據在正方向或負方向上極端的可能性有多大。為此,我們將觀察到的 _t_ 值乘以-1,因為 _t_ 分布集中在零附近,然后將兩個尾概率相加,得到一個 _ 雙尾 _p 值:
```r
pvalue_tdist_twotailed <-
pt(tStat, df = 248, lower.tail = FALSE) +
pt(-1 * tStat, df = 248, lower.tail = TRUE)
sprintf(
"p(t > %0.2f or t< %0.2f, df = 248) = %0.3f",
tStat,
-1 * tStat, pvalue_tdist_twotailed
)
```
```r
## [1] "p(t > 1.74 or t< -1.74, df = 248) = 0.084"
```
在這里我們看到,雙尾測試的 p 值是單尾測試的兩倍大,這反映了一個事實,即極端值并不令人驚訝,因為它可能發生在兩個方向上。
如何選擇是否使用單尾測試與雙尾測試?雙尾測試總是比較保守,所以使用它總是一個很好的選擇,除非你有一個非常強烈的理由使用單尾測試。在這種情況下,您應該在查看數據之前寫下假設。在第[17 章](#doing-reproducible-research)中,我們將討論假設預登記的概念,它使在您看到實際數據之前寫下假設的想法正式化。一旦你看過數據,你就不應該決定如何進行假設檢驗,因為這會給結果帶來嚴重的偏差。
#### 9.3.5.1 使用隨機化計算 p 值
到目前為止,我們已經看到了如何使用 t 分布來計算零假設下數據的概率,但是我們也可以使用模擬來實現這一點。其基本思想是,我們生成模擬數據,就像我們在零假設下所期望的那樣,然后詢問觀察到的數據與模擬數據相比有多極端。關鍵問題是:我們如何生成零假設為真的數據?一般的答案是,我們可以以一種特定的方式隨機地重新排列數據,如果空值是真的,那么數據看起來就像是真的。這類似于引導的想法,從某種意義上說,它使用我們自己的數據來得出一個答案,但它的方式不同。
##### 9.3.5.1.1 隨機化:一個簡單的例子
讓我們從一個簡單的例子開始。假設我們想將足球運動員與越野跑運動員的平均蹲起能力與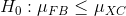和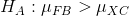進行比較。我們測量 5 名足球運動員和 5 名越野跑者的最大蹲坐能力(我們將隨機生成,假設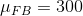、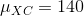和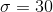。
```r
# generate simulated data for squatting ability across football players
# and cross country runners
# reset random seed for this example
set.seed(12345678)
# create a function to round values to nearest product of 5,
# to keep example simple
roundToNearest5 <- function(x, base = 5) {
return(base * round(x / base))
}
# create and show data frame containing simulated data
squatDf <- tibble(
group = as.factor(c(rep("FB", 5), rep("XC", 5))),
squat = roundToNearest5(c(rnorm(5) * 30 + 300, rnorm(5) * 30 + 140))
)
pander(squatDf)
```
<colgroup><col style="width: 11%"> <col style="width: 11%"></colgroup>
| 組 | 蹲下 |
| --- | --- |
| 聯邦調查局 | 335 個 |
| FB | 350 個 |
| FB | 230 |
| FB | 290 個 |
| FB | 325 |
| 徐克 | 115 |
| XC | 115 |
| XC | 170 個 |
| XC | 175 個 |
| XC | 215 個 |
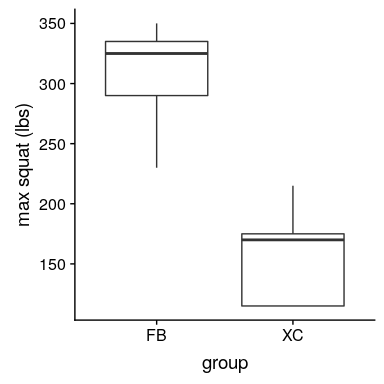
圖 9.4 足球運動員和越野跑者的模擬蹲坐能力方框圖。
從圖[9.4](#fig:squatPlot)的圖中可以清楚地看出,兩組之間存在很大的差異。我們可以使用 r 中的`t.test()`命令進行標準 t 檢驗來檢驗我們的假設:
```r
# compute and print t statistic comparing two groups
tt <-
t.test(
squat ~ group,
data = squatDf,
alternative = "greater",
var.equal = TRUE
)
sprintf("p(t > %0.2f, df = 8) = %0.5f", tt$statistic, tt$p.value)
```
```r
## [1] "p(t > 5.14, df = 8) = 0.00044"
```
這表明,在零假設下出現這種差異的可能性很小,使用 _t_ 分布來定義零。現在讓我們看看如何使用隨機化來回答相同的問題。其基本思想是,如果兩組之間沒有差異的零假設是正確的,那么一組來自哪個組(足球運動員和越野跑者)就不重要了——因此,為了創建與實際數據相似但又符合零假設的數據,我們可以隨機地為數據集中的個人排序組標簽,然后重新計算組之間的差異。這種洗牌的結果如圖[9.5](#fig:scramPlot)所示。
```r
# create a scrambled version of the group membership variable
dfScram <-
squatDf %>%
mutate(
scrambledGroup = sample(group)
) %>%
select(-group)
pander(dfScram)
```
<colgroup><col style="width: 11%"> <col style="width: 22%"></colgroup>
| squat | 加擾群 |
| --- | --- |
| 335 | FB |
| 350 | XC |
| 230 | FB |
| 290 | XC |
| 325 | XC |
| 115 | FB |
| 115 | FB |
| 170 | XC |
| 175 | FB |
| 215 | XC |
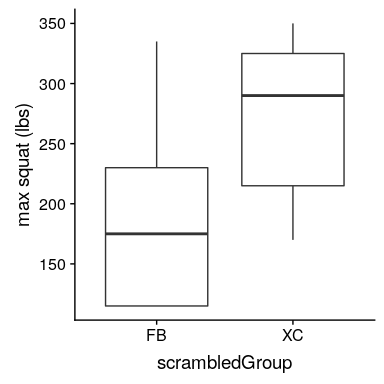
圖 9.5 加擾組標簽后分配給每組受試者的方框圖。
在把標簽弄亂之后,我們發現這兩個組現在更相似了,事實上,跨國組現在的平均值略高。現在讓我們做 10000 次,并存儲每個迭代的 t 統計信息;這可能需要一些時間來完成。
```r
# shuffle data 10,000 times and compute distribution of t values
nRuns <- 10000
shuffleAndMeasure <- function(df) {
dfScram <-
df %>%
mutate(
scrambledGroup = sample(group)
)
tt <- t.test(
squat ~ scrambledGroup,
data = dfScram,
alternative = "greater",
var.equal = TRUE
)
return(tt$statistic)
}
shuffleDiff <- replicate(nRuns, shuffleAndMeasure(squatDf))
sprintf("mean t value across shuffles = %0.3f", mean(shuffleDiff))
```
```r
## [1] "mean t value across shuffles = -0.004"
```
我們現在可以研究隨機分布的數據集中的平均差的分布。圖[9.6](#fig:shuffleHist)顯示了所有隨機隨機隨機洗牌的組差異的直方圖。正如在零假設下所預期的那樣,這個分布集中在零。
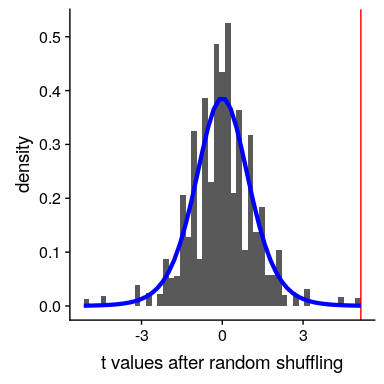
圖 9.6 隨機改組后足球和越野組之間差異的柱狀圖。紅線表示兩組間觀察到的實際差異,藍線表示本次分析的理論 t 分布。
我們可以看到,洗牌后 t 值的分布大致遵循零假設下的理論 t 分布(平均值=0),表明隨機化產生零數據的效果。如果我們將洗牌后的 t 值與實際的 t 值進行比較,我們還會看到一些有趣的事情:
```r
# compute number of runs on which t statistic for shuffle data was
# equal to observed t statistic
equalSum <- sum(shuffleDiff == tt$statistic)
sprintf("Number of runs on which shuffled t == observed t: %d", equalSum)
```
```r
## [1] "Number of runs on which shuffled t == observed t: 33"
```
```r
# compute number of runs on which t statistic for shuffle data was
# equal to observed t statistic times -1
equalSumMinus <- sum(shuffleDiff == tt$statistic * -1)
sprintf("Number of runs on which shuffled t == observed t*-1: %d", equalSumMinus)
```
```r
## [1] "Number of runs on which shuffled t == observed t*-1: 28"
```
有 33 次隨機播放,其中隨機播放數據的 t 統計值與觀察到的數據完全相同,這意味著隨機播放導致了與實際數據相同的標簽!這是不可能的,但不是 _ 不可能的,我們可以用概率論來計算它的可能性。10 個項目的可能排列數為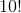,結果為 3628800。每組 5 的可能重排數為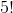,結果為 120,因此兩組 5 的可能重排數為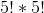或 14400。因此,我們預計 0.0039 的隨機標簽將與原始標簽完全相同,這與我們在模擬中看到的 0.0033 相當接近。我們對標簽與真實標簽完全相反的次數有著相似的期望,給出了觀察到的 t 值的負值。_
我們可以通過測量隨機數據中有多少隨機值至少與觀測值一樣極端來計算 p 值:
```r
# compute p value using randomization
pvalRandomization <- mean(shuffleDiff >= tt$statistic)
sprintf(
'p(t > %0.2f, df = 8) using randomization = %0.5f',
tt$statistic,
pvalRandomization
)
```
```r
## [1] "p(t > 5.14, df = 8) using randomization = 0.00330"
```
這個 p 值與我們用 t 分布得到的 p 值非常相似,兩者都是非常極端的,這意味著如果零假設為真,觀察到的數據就不太可能出現——在這種情況下,我們 _ 知道 _ 不是真的,因為我們生成了 E 數據。
##### 9.3.5.1.2 隨機化:體重指數/活動示例
現在讓我們使用隨機化來計算 bmi/活動示例的 p 值。在這種情況下,我們將隨機地對`PhysActive`變量進行隨機洗牌,并計算每次洗牌后組之間的差異,然后將觀察到的 t 統計量與洗牌數據集中的 t 統計量分布進行比較。
```r
# create function to shuffle BMI data
shuffleBMIstat <- function() {
bmiDataShuffled <-
NHANES_sample %>%
select(BMI, PhysActive) %>%
mutate(
PhysActive = sample(PhysActive)
)
# compute the difference
simResult <- t.test(
BMI ~ PhysActive,
data = bmiDataShuffled,
var.equal = TRUE
)
return(simResult$statistic)
}
# run function 5000 times and save output
nRuns <- 5000
meanDiffSimDf <-
data.frame(
meanDiffSim = replicate(nRuns, shuffleBMIstat())
)
```
讓我們看看結果。圖[9.7](#fig:simDiff)顯示了洗牌樣本中 t 值的分布情況,我們還可以計算發現大于或等于觀察值的概率:
```r
# compute the empirical probability of t values larger than observed
# value under the randomization null
bmtTTest <-
t.test(
BMI ~ PhysActive,
data = NHANES_sample,
var.equal = TRUE,
alternative = "greater"
)
bmiPvalRand <-
mean(meanDiffSimDf$meanDiffSim >= bmtTTest$statistic)
sprintf(
"p(mean > %0.2f, df = 248) using randomization = %0.5f",
bmtTTest$statistic,
bmiPvalRand
)
```
```r
## [1] "p(mean > 1.71, df = 248) using randomization = 0.04380"
```
```r
sprintf(
"p(mean > %0.2f, df = 248) using parametric t-test = %0.5f",
bmtTTest$statistic,
bmtTTest$p.value
)
```
```r
## [1] "p(mean > 1.71, df = 248) using parametric t-test = 0.04413"
```
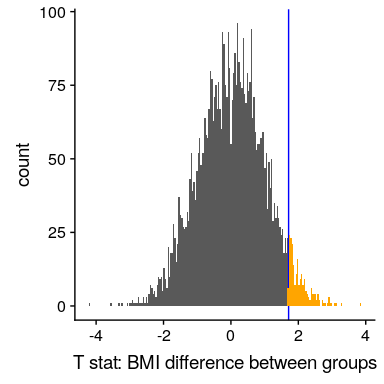
圖 9.7 組標簽洗牌后 t 統計量的柱狀圖,t 統計量的觀測值以藍線表示,其值比橙色顯示的觀測值更為極端。
同樣,隨機分組得到的 p 值(0.044)與使用 t 分布得到的 p 值(0.044)非常相似。隨機化測試的優點是,它不要求我們假設來自每個組的數據是正態分布的,盡管 T-測試通常對違反該假設的情況非常健壯。此外,隨機化檢驗可以讓我們在沒有理論分布的情況下計算統計學的 p 值,就像 t 檢驗一樣。
我們在使用隨機化測試時必須做出一個主要假設,我們稱之為 _ 互換性 _。這意味著所有的觀測都是以相同的方式分布的,這樣我們就可以在不改變總體分布的情況下交換它們。當數據中有相關的觀察結果時,這種情況就可以被打破了;例如,如果我們有來自 4 個不同家庭的個人的數據,那么我們就不能假設個人是可交換的,因為兄弟姐妹之間的距離比他們與個人之間的距離更近。來自其他家庭。一般來說,如果數據是通過隨機抽樣獲得的,那么交換性假設應該成立。
### 9.3.6 步驟 6:評估結果的“統計顯著性”
下一步是確定從上一步得到的 p 值是否足夠小,以至于我們愿意拒絕無效假設,并得出替代方案是真的。我們需要多少證據?這是統計學中最有爭議的問題之一,部分原因是它需要主觀判斷——沒有“正確”的答案。
歷史上,這個問題最常見的答案是,如果 p 值小于 0.05,我們應該拒絕無效假設。這源于羅納德·費舍爾的著作,他被稱為“20 世紀統計學中最重要的人物”(埃夫隆 1998 年):
> “如果 p 介于.1 和.9 之間,那么肯定沒有理由懷疑所測試的假設。如果低于 0.02,則強烈表明該假設不能解釋全部事實。如果我們在 0.05 點畫一條常規的線,我們就不會經常誤入歧途。在我們可以說的水平上劃一條線是很方便的:要么治療中有某種東西,要么發生了一種巧合,比如 20 次試驗中不超過一次(Fisher 1925)。
然而,費希爾從未打算將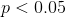作為一個固定的規則:
> “沒有一個科學工作者有一個固定的意義水平,每年,在任何情況下,他都拒絕假設;他更愿意根據自己的證據和想法來考慮每一個特定的案例”[fish:1956](fish:1956)
相反,它很可能成為一種儀式,因為在計算之前使用的 p 值表使計算統計數據任意值的 p 值變得容易。所有的表都有一個 0.05 的條目,這使得我們很容易確定一個人的統計數據是否超過了達到這一重要程度所需的值。
統計閾值的選擇仍然存在很大爭議,最近(Benjamin 等人,2018 年)有人提議將標準閾值從 0.05 更改為 0.005,這使得標準閾值更加嚴格,因此更難拒絕無效假設。在很大程度上,這一舉措是由于越來越多的擔憂,即從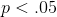的顯著結果中獲得的證據相對較弱;我們將在稍后的[17](#doing-reproducible-research)章中對再現性的討論中更詳細地討論這一點。
#### 9.3.6.1 假設檢驗作為決策:Neyman-Pearson 方法
盡管費舍爾認為 P 值可以為一個特定的假設提供證據,但是統計學家 Jerzy Neyman 和 Egon Pearson 強烈反對。相反,他們建議我們從長期來看考慮假設檢驗的錯誤率:
> “任何基于概率論的檢驗本身都不能提供任何有價值的證據來證明假設是真是假。但我們可以從另一個角度來看待測試的目的。在不希望知道每一個獨立的假設是正確還是錯誤的情況下,我們可以尋找規則來管理我們對它們的行為,在這之后,我們保證,從長期經驗來看,我們不會經常出錯”(J.Neyman 和 Pearson,1933)。
也就是說:我們不知道哪些具體的決定是正確的還是錯誤的,但是如果我們遵守規則,我們至少可以知道我們的決定會有多長時間出錯。
為了理解 Neyman 和 Pearson 開發的決策框架,我們首先需要根據可能發生的結果種類討論統計決策。存在兩種可能的現實狀態(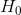為真或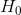為假),以及兩種可能的決定(拒絕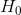或未能拒絕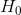)。我們可以通過兩種方式做出正確的決定:
* 當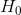為假時,我們可以決定拒絕它(在決策理論的語言中,我們稱之為 _hit_)
* 當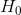為真時,我們無法拒絕它(我們稱之為 _ 正確拒絕 _)
我們還可以犯兩種錯誤:
* 當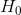為真時,我們可以決定拒絕它(我們稱之為 _ 假警報 _ 或 _ 類型 I 錯誤 _)
* 當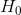實際為假時,我們無法拒絕它(我們稱之為 _Miss_ 或 _Type II Error_)
Neyman 和 Pearson 創造了兩個術語來描述從長遠來看這兩種錯誤的可能性:
* P(I 類錯誤)=
* P(II 類錯誤)=
也就是說,如果我們將設置為.05,那么從長遠來看,我們應該使 I 型錯誤占 5%。雖然通常將設置為.05,的標準值為.2-也就是說,我們愿意接受 20%的時間檢測不到真正的效果。當我們在第[10.3 節](#statistical-power)中討論統計功率時,我們將回到下面的內容,這是第二類誤差的補充。
### 9.3.7 重大結果意味著什么?
關于 p 值的實際含義有很多困惑(Gigerenzer,2004 年)。假設我們做了一個實驗,比較條件之間的平均值,我們發現 p 值為 0.01 的差異。有許多可能的解釋。
#### 9.3.7.1 是否意味著零假設為真的概率為 0.01?
不,請記住,在空假設測試中,p 值是給定空假設(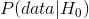)的數據概率。對于給定數據(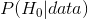)的無效假設的概率,它不保證得出結論。當我們在后面一章中討論貝葉斯推理時,我們將回到這個問題上,因為貝葉斯定理讓我們以一種可以確定后一種概率的方式反轉條件概率。
#### 9.3.7.2 這是否意味著你做出錯誤決定的概率是.01?
不,這是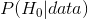,但如上所述,P 值是下數據的概率,而不是假設的概率。
#### 9.3.7.3 這是否意味著如果你再次進行研究,你將獲得 99%的相同結果?
不。p 值是一個關于特定數據集在空值下的可能性的語句;它不允許我們對未來事件(如復制)的可能性進行推斷。
#### 9.3.7.4 這是否意味著你發現了有意義的影響?
不,統計顯著性和實際顯著性之間有一個重要區別。舉個例子,假設我們進行了一項隨機對照試驗來檢驗特定飲食對體重的影響,我們發現在 P<;.05 有統計學意義的影響。這并不能告訴我們實際損失了多少重量,我們稱之為 _ 效應大小 _(將在[10](#ci-effect-size-power)章中詳細討論)。如果我們考慮一項關于減肥的研究,那么我們可能不會認為十盎司的減肥(即一袋薯片的重量)實際上是非常重要的。讓我們看看我們的能力,檢測 1 盎司的顯著差異,隨著樣本量的增加。
```r
# create simulated data for weight loss trial
weightLossTrial <- function(nPerGroup, weightLossOz = 1) {
# mean and SD in Kg based on NHANES adult dataset
kgToOz <- 35.27396195 # conversion constant for Kg to Oz
meanOz <- 81.78 * kgToOz
sdOz <- 21.29 * kgToOz
# create data
controlGroup <- rnorm(nPerGroup) * sdOz + meanOz
expGroup <- rnorm(nPerGroup) * sdOz + meanOz - weightLossOz
ttResult <- t.test(expGroup, controlGroup)
return(c(
nPerGroup, weightLossOz, ttResult$p.value,
diff(ttResult$estimate)
))
}
nRuns <- 1000
sampSizes <- 2**seq(5,17) # powers of 2
simResults <- c() ## create an empty list to add results onto
for (i in 1:length(sampSizes)) {
tmpResults <- replicate(
nRuns,
weightLossTrial(sampSizes[i], weightLossOz = 10)
)
summaryResults <- c(
tmpResults[1, 1], tmpResults[2, 1],
sum(tmpResults[3, ] < 0.05),
mean(tmpResults[4, ])
)
simResults <- rbind(simResults, summaryResults)
}
simResultsDf <-
as.tibble(simResults) %>%
rename(
sampleSize = V1,
effectSizeLbs = V2,
nSigResults = V3,
meanEffect = V4
) %>%
mutate(pSigResult = nSigResults / nRuns)
```
圖[9.8](#fig:sigResults)顯示了顯著結果的比例如何隨著樣本量的增加而增加,這樣,當樣本量非常大(總共約 262000 名受試者)時,當體重減少 1 盎司時,我們將在 90%以上的研究中發現顯著結果。盡管這些在統計學上有顯著意義,但大多數醫生認為一盎司的體重減輕在實際或臨床上并不重要。當我們回到[10.3 節](#statistical-power)中的 _ 統計冪 _ 概念時,我們將更詳細地探討這一關系,但從這個例子中應該已經清楚,統計顯著性并不一定表示實際意義。
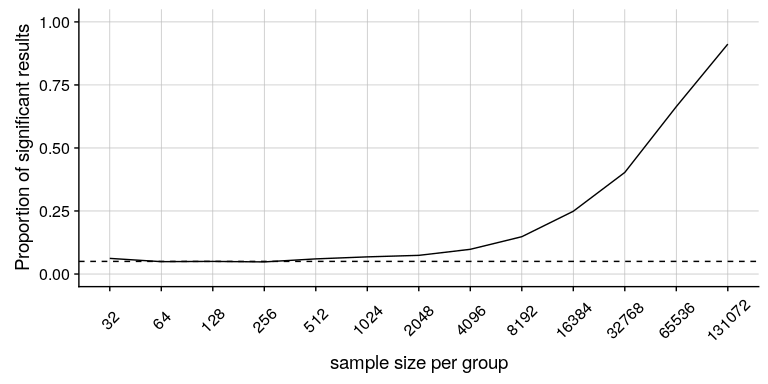
圖 9.8 作為樣本量函數的一個非常小的變化(1 盎司,約 0.001 標準偏差)的顯著性比例。
- 前言
- 0.1 本書為什么存在?
- 0.2 你不是統計學家-我們為什么要聽你的?
- 0.3 為什么是 R?
- 0.4 數據的黃金時代
- 0.5 開源書籍
- 0.6 確認
- 1 引言
- 1.1 什么是統計思維?
- 1.2 統計數據能為我們做什么?
- 1.3 統計學的基本概念
- 1.4 因果關系與統計
- 1.5 閱讀建議
- 2 處理數據
- 2.1 什么是數據?
- 2.2 測量尺度
- 2.3 什么是良好的測量?
- 2.4 閱讀建議
- 3 概率
- 3.1 什么是概率?
- 3.2 我們如何確定概率?
- 3.3 概率分布
- 3.4 條件概率
- 3.5 根據數據計算條件概率
- 3.6 獨立性
- 3.7 逆轉條件概率:貝葉斯規則
- 3.8 數據學習
- 3.9 優勢比
- 3.10 概率是什么意思?
- 3.11 閱讀建議
- 4 匯總數據
- 4.1 為什么要總結數據?
- 4.2 使用表格匯總數據
- 4.3 分布的理想化表示
- 4.4 閱讀建議
- 5 將模型擬合到數據
- 5.1 什么是模型?
- 5.2 統計建模:示例
- 5.3 什么使模型“良好”?
- 5.4 模型是否太好?
- 5.5 最簡單的模型:平均值
- 5.6 模式
- 5.7 變異性:平均值與數據的擬合程度如何?
- 5.8 使用模擬了解統計數據
- 5.9 Z 分數
- 6 數據可視化
- 6.1 數據可視化如何拯救生命
- 6.2 繪圖解剖
- 6.3 使用 ggplot 在 R 中繪制
- 6.4 良好可視化原則
- 6.5 最大化數據/墨水比
- 6.6 避免圖表垃圾
- 6.7 避免數據失真
- 6.8 謊言因素
- 6.9 記住人的局限性
- 6.10 其他因素的修正
- 6.11 建議閱讀和視頻
- 7 取樣
- 7.1 我們如何取樣?
- 7.2 采樣誤差
- 7.3 平均值的標準誤差
- 7.4 中心極限定理
- 7.5 置信區間
- 7.6 閱讀建議
- 8 重新采樣和模擬
- 8.1 蒙特卡羅模擬
- 8.2 統計的隨機性
- 8.3 生成隨機數
- 8.4 使用蒙特卡羅模擬
- 8.5 使用模擬統計:引導程序
- 8.6 閱讀建議
- 9 假設檢驗
- 9.1 無效假設統計檢驗(NHST)
- 9.2 無效假設統計檢驗:一個例子
- 9.3 無效假設檢驗過程
- 9.4 現代環境下的 NHST:多重測試
- 9.5 閱讀建議
- 10 置信區間、效應大小和統計功率
- 10.1 置信區間
- 10.2 效果大小
- 10.3 統計能力
- 10.4 閱讀建議
- 11 貝葉斯統計
- 11.1 生成模型
- 11.2 貝葉斯定理與逆推理
- 11.3 進行貝葉斯估計
- 11.4 估計后驗分布
- 11.5 選擇優先權
- 11.6 貝葉斯假設檢驗
- 11.7 閱讀建議
- 12 分類關系建模
- 12.1 示例:糖果顏色
- 12.2 皮爾遜卡方檢驗
- 12.3 應急表及雙向試驗
- 12.4 標準化殘差
- 12.5 優勢比
- 12.6 貝葉斯系數
- 12.7 超出 2 x 2 表的分類分析
- 12.8 注意辛普森悖論
- 13 建模持續關系
- 13.1 一個例子:仇恨犯罪和收入不平等
- 13.2 收入不平等是否與仇恨犯罪有關?
- 13.3 協方差和相關性
- 13.4 相關性和因果關系
- 13.5 閱讀建議
- 14 一般線性模型
- 14.1 線性回歸
- 14.2 安裝更復雜的模型
- 14.3 變量之間的相互作用
- 14.4“預測”的真正含義是什么?
- 14.5 閱讀建議
- 15 比較方法
- 15.1 學生 T 考試
- 15.2 t 檢驗作為線性模型
- 15.3 平均差的貝葉斯因子
- 15.4 配對 t 檢驗
- 15.5 比較兩種以上的方法
- 16 統計建模過程:一個實例
- 16.1 統計建模過程
- 17 做重復性研究
- 17.1 我們認為科學應該如何運作
- 17.2 科學(有時)是如何工作的
- 17.3 科學中的再現性危機
- 17.4 有問題的研究實踐
- 17.5 進行重復性研究
- 17.6 進行重復性數據分析
- 17.7 結論:提高科學水平
- 17.8 閱讀建議
- References
