## 12.3 應急表及雙向試驗 我們經常使用卡方檢驗的另一種方法是詢問兩個分類變量是否相互關聯。作為一個更現實的例子，讓我們來考慮一個問題，當一個黑人司機被警察攔下時，他們是否比一個白人司機更有可能被搜查，斯坦福公開警務項目（[https://open policing.stanford.edu/](https://openpolicing.stanford.edu/)）研究了這個問題，并提供了我們可以用來分析問題的數據。我們將使用來自康涅狄格州的數據，因為它們相當小。首先清理這些數據，以刪除所有不必要的數據（參見 code/process_ct_data.py）。 ```r # load police stop data stopData <- read_csv("data/CT_data_cleaned.csv") %>% rename(searched = search_conducted) ``` 表示分類分析數據的標準方法是通過 _ 列聯表 _，列聯表顯示了屬于每個變量值的每個可能組合的觀測值的數量或比例。 讓我們計算一下警察搜索數據的應急表： ```r # compute and print two-way contingency table summaryDf2way <- stopData %>% count(searched, driver_race) %>% arrange(driver_race, searched) summaryContingencyTable <- summaryDf2way %>% spread(driver_race, n) pander(summaryContingencyTable) ``` <colgroup><col style="width: 15%"> <col style="width: 11%"> <col style="width: 11%"></colgroup> | 已搜索 | 黑色 | 白色 | | --- | --- | --- | | 錯誤的 | 36244 個 | 239241 個 | | 真的 | 1219 年 | 3108 個 | 使用比例而不是原始數字查看應急表也很有用，因為它們更容易在視覺上進行比較。 ```r # Compute and print contingency table using proportions # rather than raw frequencies summaryContingencyTableProportion <- summaryContingencyTable %>% mutate( Black = Black / nrow(stopData), #count of Black individuals searched / total searched White = White / nrow(stopData) ) pander(summaryContingencyTableProportion, round = 4) ``` <colgroup><col style="width: 15%"> <col style="width: 12%"> <col style="width: 12%"></colgroup> | searched | Black | White | | --- | --- | --- | | FALSE | 0.1295 年 | 0.855 個 | | TRUE | 0.0044 美元 | 0.0111 個 | Pearson 卡方檢驗允許我們檢驗觀察到的頻率是否與預期頻率不同，因此我們需要確定如果搜索和種族不相關，我們期望在每個細胞中出現的頻率，我們可以定義為 _ 獨立。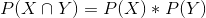_ 請記住，如果 x 和 y 是獨立的，那么：  也就是說，零獨立假設下的聯合概率僅僅是每個變量的 _ 邊際 _ 概率的乘積。邊際概率只是每一個事件發生的概率，與其他事件無關。我們可以計算這些邊際概率，然后將它們相乘，得到獨立狀態下的預期比例。 | | 黑色 | 白色 | | | --- | --- | --- | --- | | 未搜索 | P（ns）*P（b） | P（ns）*P（w） | P（納秒） | | 已搜索 | P（S）*P（B） | P（S）*P（W） | P（S） | | | P（B） | P（寬） | | 我們可以使用稱為“外積”的線性代數技巧（通過`outer()`函數）來輕松計算。 ```r # first, compute the marginal probabilities # probability of being each race summaryDfRace <- stopData %>% count(driver_race) %>% #count the number of drivers of each race mutate( prop = n / sum(n) #compute the proportion of each race out of all drivers ) # probability of being searched summaryDfStop <- stopData %>% count(searched) %>% #count the number of searched vs. not searched mutate( prop = n / sum(n) # compute proportion of each outcome out all traffic stops ) ``` ```r # second, multiply outer product by n (all stops) to compute expected frequencies expected <- outer(summaryDfRace$prop, summaryDfStop$prop) * nrow(stopData) # create a data frame of expected frequencies for each race expectedDf <- data.frame(expected, driverRace = c("Black", "White")) %>% rename( NotSearched = X1, Searched = X2 ) # tidy the data frame expectedDfTidy <- gather(expectedDf, searched, n, -driverRace) %>% arrange(driverRace, searched) ``` ```r # third, add expected frequencies to the original summary table # and fourth, compute the standardized squared difference between # the observed and expected frequences summaryDf2way <- summaryDf2way %>% mutate(expected = expectedDfTidy$n) summaryDf2way <- summaryDf2way %>% mutate(stdSqDiff = (n - expected)**2 / expected) pander(summaryDf2way) ``` <colgroup><col style="width: 15%"> <col style="width: 19%"> <col style="width: 12%"> <col style="width: 15%"> <col style="width: 15%"></colgroup> | searched | 車手比賽 | N 號 | 預期 | 標準平方差 | | --- | --- | --- | --- | --- | | FALSE | 黑色 | 36244 | 36883.67 個 | 2009 年 11 月 | | TRUE | Black | 1219 | 579.33 條 | 第 706.31 條 | | FALSE | 白色 | 239241 | 238601.3 條 | 1.71 條 | | TRUE | White | 3108 | 3747.67 美元 | 109.18 條 | ```r # finally, compute chi-squared statistic by # summing the standardized squared differences chisq <- sum(summaryDf2way$stdSqDiff) sprintf("Chi-squared value = %0.2f", chisq) ``` ```r ## [1] "Chi-squared value = 828.30" ``` 在計算了卡方統計之后，我們現在需要將其與卡方分布進行比較，以確定它與我們在無效假設下的期望相比有多極端。這種分布的自由度是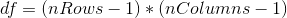——因此，對于類似于這里的 2x2 表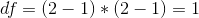，。這里的直覺是計算預期頻率需要我們使用三個值：觀察總數和兩個變量的邊際概率。因此，一旦計算出這些值，就只有一個數字可以自由變化，因此有一個自由度。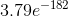鑒于此，我們可以計算卡方統計的 p 值： ```r pval <- pchisq(chisq, df = 1, lower.tail = FALSE) sprintf("p-value = %e", pval) ``` ```r ## [1] "p-value = 3.795669e-182" ``` 的 p 值非常小，表明如果種族和警察搜查之間真的沒有關系，觀察到的數據就不太可能，因此我們應該拒絕獨立性的無效假設。 我們還可以使用 r 中的`chisq.test()`函數輕松執行此測試： ```r # first need to rearrange the data into a 2x2 table summaryDf2wayTable <- summaryDf2way %>% dplyr::select(-expected, -stdSqDiff) %>% spread(searched, n) %>% dplyr::select(-driver_race) chisqTestResult <- chisq.test(summaryDf2wayTable, 1, correct = FALSE) chisqTestResult ``` ```r ## ## Pearson's Chi-squared test ## ## data: summaryDf2wayTable ## X-squared = 800, df = 1, p-value <2e-16 ```