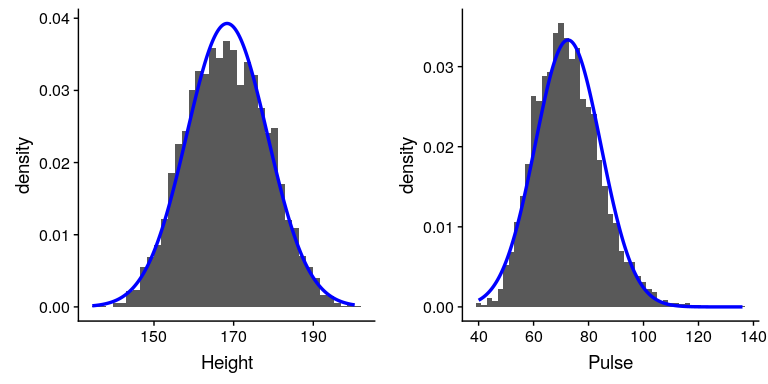
## 4.3 分布的理想化表示 數據集就像雪花，因為每一個都是不同的，但盡管如此，在不同類型的數據中經常會看到一些模式。這允許我們使用理想化的數據表示來進一步總結它們。讓我們用[4.5](#fig:heightHistSep)中繪制的成人身高數據，并將它們與一個非常不同的變量一起繪制：脈率（每分鐘心跳），也用 nhanes 測量（見圖[4.6](#fig:NormalDistPlotsWithDist)）。  圖 4.6 nhanes 數據集中高度（左）和脈沖（右）的柱狀圖，每個數據集中的正態分布重疊。 雖然這些情節看起來不完全相同，但都具有在中間圓頂上相對對稱的一般特征。這個形狀實際上是我們收集數據時常見的分布形狀之一，我們稱之為 _ 正態 _（或 _ 高斯 _）分布。該分布由兩個值（我們稱之為分布的 _ 參數 _）定義：中心峰的位置（我們稱之為 _ 平均值 _）和分布的寬度（用稱為 _ 標準偏差的參數描述）。操作 _）。圖[4.6](#fig:NormalDistPlotsWithDist)顯示了在每個歷史程序頂部繪制的適當正態分布。您可以看到，雖然曲線不完全符合數據，但它們在描述分布方面做得很好——只有兩個數字！ 正如我們在后面的課程中討論中心極限定理時所看到的，世界上許多變量呈現正態分布的形式有一個深刻的數學原因。 ### 4.3.1 偏斜度 圖[4.6](#fig:NormalDistPlotsWithDist)中的例子很好地遵循正態分布，但在許多情況下，數據將以系統的方式偏離正態分布。數據可以偏離的一種方式是不對稱的，這樣分布的一個尾部比另一個更加密集。我們稱之為“歪斜”。偏度通常發生在測量被限制為非負值的情況下，例如我們計算事物或測量經過的時間（因此變量不能取負值）。 斜率的一個例子可以在舊金山國際機場機場安全線的平均等待時間中看到，在圖 [4.7 的左側面板](#fig:SFOWaitTimes)中繪制。您可以看到，雖然大多數等待時間不到 20 分鐘，但有許多情況下，它們會更長，超過 60 分鐘！這是一個“右偏”分布的例子，其中右尾比左尾長；在查看計數或測量時間時，這些是常見的，不能小于零。看到“左偏”分布不太常見，但它們可能發生，例如，當查看不能取大于 1 的值的分數值時。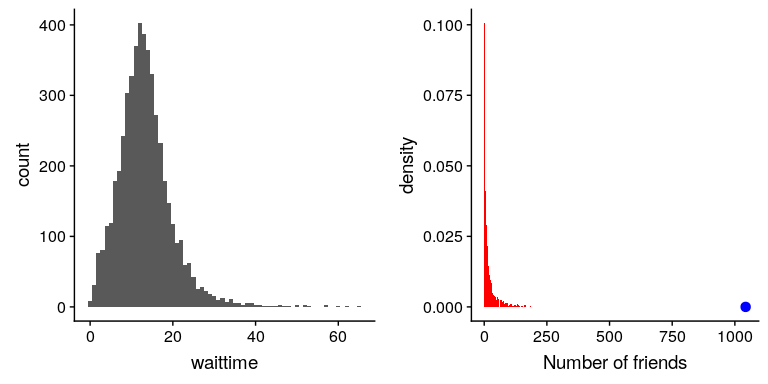  圖 4.7 右偏和長尾分布示例。左：從[https://awt.cbp.gov/](https://awt.cbp.gov/)獲取的 SFO 終端 A 安全的平均等待時間（2017 年 1-10 月）。右圖：從斯坦福大型網絡數據庫中獲取的 3663 個人中 Facebook 好友數量的柱狀圖。朋友最多的人用藍點表示。 ### 4.3.2 長尾分布 歷史上，統計數據主要集中在正態分布的數據上，但有許多數據類型看起來與正態分布完全不同。特別是，許多現實世界的分布是“長尾巴”，這意味著右尾巴遠遠超出了分布中最典型的成員。一種最有趣的數據類型，其中長尾分布發生在社會網絡的分析。例如，讓我們看看來自斯坦福大網絡數據庫[的 Facebook 好友數據，并繪制數據庫中 3663 人的好友數量柱狀圖（參見圖](https://snap.stanford.edu/data/egonets-Facebook.html)[4.7](#fig:SFOWaitTimes)的右面板）。如我們所見，這個分布有一個很長的右尾——一般人有 24.09 個朋友，而朋友最多的人（用藍點表示）有 1043 個！ 在現實世界中，長尾分布越來越被認可。特別是，復雜系統的許多特征都具有這些分布特征，從文本中的單詞頻率，到進出機場的航班數量，再到大腦網絡的連接。有許多不同的方法可以實現長尾分布，但在基督教圣經中所謂的“馬太效應”的情況下會出現一個常見的方法： > 因為凡有更多的，必被賜給他，他也必富足；但沒有的，連他所擁有的，也必被奪去。-馬太福音 25:29，修訂后的標準版 通常被解釋為“富人越富有”。在這種情況下，優勢是復合的，這樣那些有更多朋友的人可以接觸到更多的新朋友，而那些有更多錢的人可以做更多能增加他們財富的事情。 隨著課程的發展，我們將看到一些長尾分布的例子，我們應該記住，當面對長尾數據時，統計中的許多工具可能會失敗。正如納西姆·尼古拉斯·塔勒布在其《黑天鵝》一書中指出的那樣，這種長尾分布在 2008 年金融危機中起到了至關重要的作用，因為交易員使用的許多金融模型都假設金融系統將遵循正態分布，而他們顯然沒有遵循正態分布。