## 17.3 科學中的再現性危機 人們可能希望布萊恩·萬辛克是一個罕見的異類，但越來越清楚的是，在科學中，再現性問題比以前想象的要普遍得多。這一點在 2015 年變得清晰起來，當時一大群研究人員在名為“評估心理科學的再現性”的雜志 _Science_ 上發表了一項研究（開放科學合作 2015）。在這項研究中，研究者們選取了 100 項已發表的心理學研究成果，并試圖復制論文最初報道的結果。他們的發現令人震驚：盡管 97%的原始論文報告了具有統計學意義的發現，但在復制研究中只有 37%的這些影響具有統計學意義。盡管心理學中的這些問題受到了廣泛關注，但它們似乎存在于幾乎所有科學領域，從癌癥生物學（Errington 等人 2014 年）和化學（Baker 2017 年）到經濟學（Christensen 和 Miguel 2016 年）和社會科學（Camerer 等人 2018 年）。 2010 年之后出現的再現性危機實際上是由斯坦福大學的一位醫生約翰·伊奧尼迪斯預測的，他在 2005 年寫了一篇題為“為什么大多數發表的研究結果都是錯誤的”（伊奧尼迪斯，2005 年）的論文。在本文中，伊奧尼迪斯認為，在現代科學的背景下使用零假設統計檢驗必然會導致高水平的錯誤結果。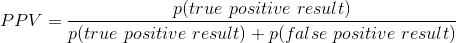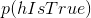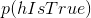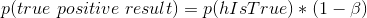 ### 17.3.1 陽性預測值及統計意義 ioannidis 的分析側重于一個被稱為 _ 陽性預測值 _ 的概念，定義為陽性結果（通常翻譯為“統計顯著結果”）的比例，這是正確的：  假設我們知道我們的假設是正確的概率（），那么一個真正的正結果的概率就是乘以研究的統計能力：  were為假陰性率。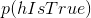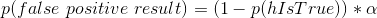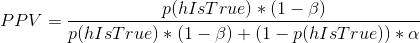假陽性結果的概率由和假陽性率決定：  PPV 的定義如下：  我們先舉一個例子，假設為真的概率很高，比如說 0.8——但是請注意，一般來說，我們不能真正知道這個概率。假設我們使用標準值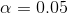和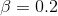進行研究。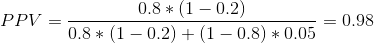我們可以將 ppv 計算為：  這意味著，如果我們在一項假設很可能是真實的、權力很高的研究中發現一個積極的結果，那么它成為真實的可能性很高。然而，請注意，假設具有如此高的真實可能性的研究領域可能不是一個非常有趣的研究領域；當研究告訴我們一些新的東西時，它是最重要的！ 讓我們對一個字段進行相同的分析，其中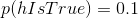——也就是說，測試的大多數假設都是錯誤的。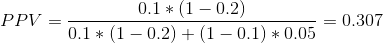在這種情況下，PPV 是：  這意味著，在一個大多數假設都可能是錯誤的領域（也就是說，一個有趣的科學領域，研究人員正在測試風險假設），即使我們發現了一個積極的結果，也更可能是錯誤的，而不是真的！事實上，這只是我們在假設檢驗中討論的基礎利率效應的另一個例子——當結果不太可能出現時，幾乎可以肯定的是，大多數積極的結果將是假陽性。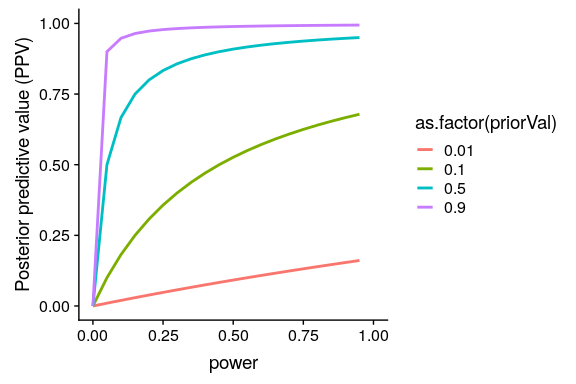 我們可以模擬這一點，以顯示 ppv 與統計功率的關系，作為假設為真的先驗概率的函數（參見圖[17.1](#fig:PPVsim)）  圖 17.1 后驗預測值作為統計功率函數（繪制在 x 軸上）的模擬，假設的前驗概率為真（繪制為單獨的線）。 不幸的是，許多科學領域的統計能力仍然很低（Smaldino 和 McElreath，2016 年），這表明許多已發表的研究結果都是錯誤的。 ### 17.3.2 勝利者的詛咒 另一種錯誤也可能發生在統計能力較低的時候：我們對影響大小的估計將被夸大。這種現象經常被稱為“贏家的詛咒”，它來自經濟學，它指的是，對于某些類型的拍賣（每個人的價值都是一樣的，就像一罐 25 美分的硬幣，而競拍是私人的），贏家幾乎總是支付比好的東西更高的價格。.在科學中，贏家的詛咒是指根據重大結果（即贏家）估計的效果大小幾乎總是高估真實效果大小的事實。 我們可以對此進行模擬，以了解重要結果的估計效果大小與實際潛在效果大小之間的關系。讓我們生成真實效果大小為 0.2 的數據，并在檢測到顯著效果的情況下估計這些結果的效果大小。圖[17.2](#fig:CurseSim)顯示，當功率較低時，與實際效果大小相比，顯著結果的估計效果大小可能會大大膨脹。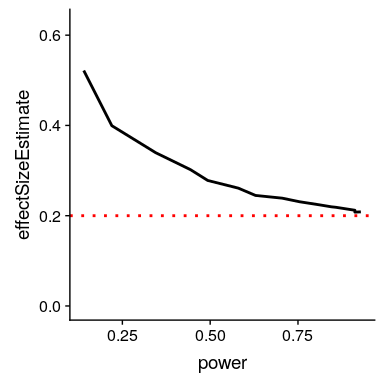  圖 17.2 勝利者詛咒作為統計冪函數（x 軸）的模擬。黑線顯示估計的效果大小，紅色虛線顯示實際的效果大小。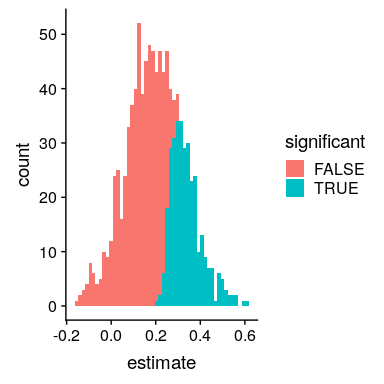  圖 17.3 一個柱狀圖，顯示數據集中若干樣本的樣本大小，顯著結果以藍色顯示，非顯著結果以紅色顯示。 我們可以通過一個模擬來了解為什么會出現這種情況。在圖[17.3](#fig:curseSimSingle)中，您可以看到 1000 個樣本的估計效果大小的柱狀圖，通過測試是否具有統計意義來分隔。從圖中可以清楚地看到，如果我們僅僅根據顯著的結果來估計效果大小，那么我們的估計就會膨脹；只有當大多數結果都是顯著的（即功率高，效果相對較大）時，我們的估計才會接近實際的效果大小。