## 8.3 生成隨機數 運行蒙特卡羅模擬需要我們生成隨機數。只有通過物理過程才能生成真正的隨機數（即完全不可預測的數），例如原子衰變或骰子滾動，這些過程很難獲得和/或太慢，無法用于計算機模擬（盡管可以從[NIST 隨機信標](https://www.nist.gov/programs-projects/nist-randomness-beacon%5D)）。 一般來說，我們使用計算機算法生成的 _ 偽隨機 _ 數字來代替真正的隨機數；從難以預測的意義上講，這些數字看起來是隨機的，但實際上這些數字序列在某一點上會重復出現。例如，R 中使用的隨機數生成器將在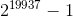個數之后重復。這遠遠超過了宇宙歷史上的秒數，我們一般認為這對于統計分析的大多數目的來說都是好的。 在 R 中，有一個函數可以為每個主要概率分布生成隨機數，例如： * `runif()`-均勻分布（0 和 1 之間的所有值相等） * `rnorm()`-正態分布 * `rbinom()`-二項分布（如擲骰子、擲硬幣） 圖[8.1](#fig:rngExamples)顯示了使用`runif()`和`rnorm()`函數生成的數字示例，這些函數使用以下代碼生成： ```r p1 <- tibble( x = runif(10000) ) %>% ggplot((aes(x))) + geom_histogram(bins = 100) + labs(title = "Uniform") p2 <- tibble( x = rnorm(10000) ) %>% ggplot(aes(x)) + geom_histogram(bins = 100) + labs(title = "Normal") plot_grid(p1, p2, ncol = 3) ```  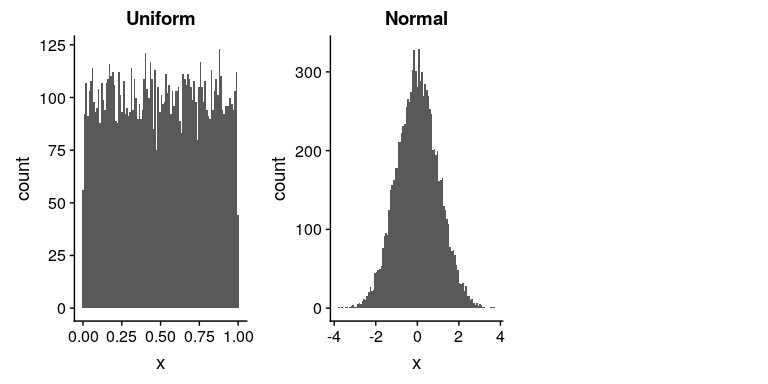圖 8.1 由均勻（左）或正態（右）分布生成的隨機數示例。 如果您有一個 _ 分位數 _ 函數用于分發，您還可以為任何分發生成隨機數。這是累積分布函數的倒數；分位數函數不是確定一組值的累積概率，而是確定一組累積概率的值。使用分位數函數，我們可以從均勻分布中生成隨機數，然后通過它的分位數函數將其映射到興趣分布中。 默認情況下，每次運行上面描述的隨機數生成器函數之一時，R 都會生成一組不同的隨機數。但是，通過將所謂的 _ 隨機種子 _ 設置為特定值，也可以生成完全相同的隨機數集。我們將在本書中的許多示例中這樣做，以確保示例是可重復的。 ```r # if we run the rnorm() command twice, it will give us different sets of pseudorandom numbers each time print(rnorm(n = 5)) ``` ```r ## [1] 1.48 0.18 0.21 -0.15 -1.72 ``` ```r print(rnorm(n = 5)) ``` ```r ## [1] -0.691 -2.231 0.391 0.029 -0.647 ``` ```r # if we set the random seed to the same value each time, then it will give us the same series of pseudorandom numbers each time. set.seed(12345) print(rnorm(n = 5)) ``` ```r ## [1] 0.59 0.71 -0.11 -0.45 0.61 ``` ```r set.seed(12345) print(rnorm(n = 5)) ``` ```r ## [1] 0.59 0.71 -0.11 -0.45 0.61 ```