# 三、神經網絡：感知機 自最近十年以來，神經網絡一直處于機器學習研究和應用的最前沿。 **深層神經網絡**（**DNN**），傳遞學習以及計算效率高的 GPU 的可用性已幫助在圖像識別，語音識別甚至文本生成領域取得了重大進展。 在本章中，我們將專注于基本的神經網絡感知機，即人工神經元的完全連接的分層架構。 本章將包括以下秘籍： * 激活函數 * 單層感知機 * 反向傳播算法的梯度計算 * 使用 MLP 的 MNIST 分類器 * 使用 MLP 進行函數逼近-預測波士頓房價 * 調整超參數 * 更高級別的 API -- Keras # 介紹 神經網絡，通常也稱為**連接器模型**，是受人腦啟發的。 像人的大腦一樣，神經網絡是通過稱為**權重**的突觸強度相互連接的大量人工神經元的集合。 正如我們通過長輩提供給我們的示例進行學習一樣，人工神經網絡也可以通過作為訓練數據集提供給他們的示例進行學習。 有了足夠數量的訓練數據集，人工神經網絡可以概括信息，然后也可以將其用于看不見的數據。 太棒了，它們聽起來像魔術！ 神經網絡并不是什么新鮮事物。 第一個神經網絡模型由 [McCulloch Pitts（MCP）](http://vordenker.de/ggphilosophy/mcculloch_a-logical-calculus.pdf)最早在 1943 年提出。 建造了第一臺計算機！）該模型可以執行 AND/OR/NOT 之類的邏輯運算。 MCP 模型具有固定的權重和偏差； 沒有學習的可能。 幾年后，[Frank Rosenblatt 在 1958 年解決了這個問題](https://blogs.umass.edu/brain-wars/files/2016/03/rosenblatt-1957.pdf)。 他提出了第一個學習神經網絡，稱為**感知機**。 從那時起，眾所周知，添加多層神經元并建立一個深而密集的網絡將有助于神經網絡解決復雜的任務。 正如母親為孩子的成就感到自豪一樣，科學家和工程師對使用[**神經網絡**（**NN**）](https://www.youtube.com/watch?v=jPHUlQiwD9Y)。 這些聲明不是虛假的，但是由于硬件計算的限制和復雜的網絡結構，當時根本不可能實現它們。 這導致了 1970 年代和 1980 年代的 **AI 寒冬**。 在這些寒戰中，由于很少或幾乎沒有對基于 AI 的項目提供資金，因此該領域的進展放緩了。 隨著 DNN 和 GPU 的出現，情況發生了變化。 今天，我們擁有的網絡可以在較少的調整參數的情況下實現更好的表現，諸如丟棄和遷移學習之類的技術可以進一步減少訓練時間，最后，硬件公司正在提出專門的硬件芯片來執行基于 NN 的快速計算。 人工神經元是所有神經網絡的核心。 它由兩個主要部分組成-加法器（對加權后的神經元的所有輸入求和），以及處理單元，對加權后的總和進行加權，并基于稱為**激活函數**的預定義函數生成輸出。 。 每個人工神經元都有其自己的一組權重和閾值（偏差）。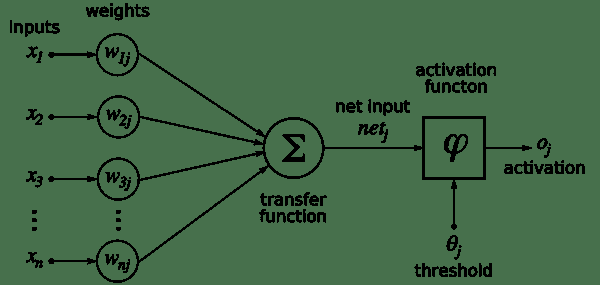 它通過不同的學習算法來學習這些權重和閾值：  [來源](https://commons.wikimedia.org/wiki/File:Rosenblattperceptron.png) 當僅存在此類神經元的一層時，它稱為感知機。 輸入層稱為**第零層**，因為它僅緩沖輸入。 存在的唯一神經元層形成輸出層。 輸出層的每個神經元都有自己的權重和閾值。 當存在許多這樣的層時，該網絡稱為**多層感知機**（**MLP**）。 一個 MLP 具有一個或多個隱藏層。 這些隱藏層具有不同數量的隱藏神經元。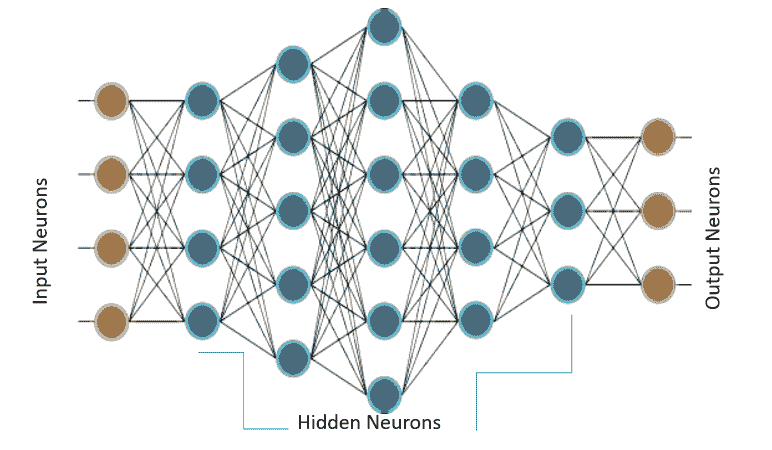 每個隱藏層的神經元具有相同的激活函數：  上圖顯示了一個 MLP，它具有四個輸入，五個隱藏層，每個隱藏層分別具有 4、5、6、4 和 3 個神經元，而在輸出層中具有三個神經元。 在 MLP 中，下層的所有神經元都與其上一層的所有神經元相連。 因此，MLP 也稱為**全連接層**。 MLP 中的信息流始終是從輸入到輸出。 由于沒有反饋或跳躍，因此這些網絡也稱為**前饋網絡**。 使用**梯度下降算法**訓練感知機。 在第 2 章“回歸”中，您了解了梯度下降； 在這里，我們對其進行更深入的研究。 感知機通過有監督的學習算法進行學習，也就是說，網絡由訓練數據集中存在的所有輸入的期望輸出提供。 在輸出中，我們定義一個誤差函數或目標函數`J(W)`，這樣，當網絡完全學習了所有訓練數據時，目標函數將最小。 更新輸出層和隱藏層的權重，以使目標函數的梯度減小：  為了更好地理解它，請對山丘，高原和坑坑洼洼的景觀進行可視化處理。 目的是扎根（目標函數的全局最小值）。 如果您站在山頂上而必須下山，那么很明顯的選擇是，您將沿著山下坡，即向負坡度（或負坡度）移動。 以相同的方式，感知機中的權重與目標函數的梯度的負值成比例地變化。 梯度值越高，權重值的變化越大，反之亦然。 現在，這一切都很好，但是當梯度達到零，因此權重沒有變化時，我們到達高原時就會遇到問題。 當我們進入一個小坑（局部極小值）時，我們也可能遇到問題，因為當我們嘗試移動到任一側時，坡度將增加，從而迫使網絡停留在坑中。 如第 2 章，“回歸”中所討論的，梯度下降有多種變體，旨在提高收斂性，避免了陷入局部極小值或高原的問題（增加動量，可變學習率）。 TensorFlow 借助不同的優化器自動計算這些梯度。 但是，需要注意的重要一點是，由于 TensorFlow 將計算梯度，而梯度也將涉及激活函數的導數，因此重要的是，您選擇的激活函數是可微的，并且在整個訓練場景中最好具有非零梯度 。 感知機梯度下降的主要方法之一不同于第 2 章，“回歸”，應用是為輸出層定義目標函數，但可用于查找目標層，以及隱藏層的神經元的權重變化。 這是使用**反向傳播**（**BPN**）算法完成的，其中輸出端的誤差會向后傳播到隱藏層，并用于確定權重變化。 您將很快了解更多信息。 # 激活函數 每個神經元必須具有激活函數。 它們使神經元具有建模復雜非線性數據集所需的非線性特性。 該函數獲取所有輸入的加權和，并生成一個輸出信號。 您可以將其視為輸入和輸出之間的轉換。 使用適當的激活函數，我們可以將輸出值限制在定義的范圍內。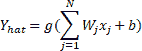 如果`x[j]`是第`j`個輸入，則`W[j]`的第`j`行輸入到我們的神經元，并且`b`是我們神經元的偏置，即神經元的輸出（從生物學的角度來說，是神經元的發射） 通過激活函數，在數學上表示為：  在此， `g`表示激活函數。 激活函數`∑(W[j]x[j]) + b`的參數稱為神經元的**激活**。 # 準備 我們對給定輸入刺激的反應受神經元激活函數的控制。 有時我們的回答是二進制的是或否。 例如，當開個玩笑時，我們要么笑要么不笑。 在其他時間，響應似乎是線性的，例如由于疼痛而哭泣。 有時，響應似乎在一定范圍內。 模仿類似的行為，人工神經元使用了許多不同的激活函數。 在本秘籍中，您將學習如何在 TensorFlow 中定義和使用一些常見的激活函數。 # 操作步驟 我們繼續執行激活函數，如下所示： 1. **閾值激活函數**：這是最簡單的激活函數。 在此，如果神經元的活動性大于零，則神經元會觸發；否則，神經元會觸發。 否則，它不會觸發。 這是閾值激活函數隨神經元活動變化而變化的圖，以及在 TensorFlow 中實現閾值激活函數的代碼： ```py import tensorflow as tf import numpy as np import matplotlib.pyplot as plt # Threshold Activation function def threshold (x): cond = tf.less(x, tf.zeros(tf.shape(x), dtype = x.dtype)) out = tf.where(cond, tf.zeros(tf.shape(x)), tf.ones(tf.shape(x))) return out # Plotting Threshold Activation Function h = np.linspace(-1,1,50) out = threshold(h) init = tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) y = sess.run(out) plt.xlabel('Activity of Neuron') plt.ylabel('Output of Neuron') plt.title('Threshold Activation Function') plt.plot(h, y) ``` 以下是上述代碼的輸出：  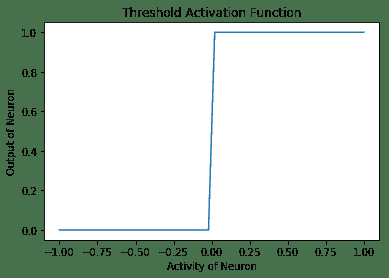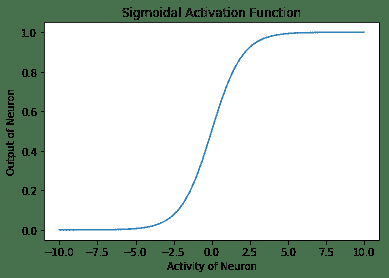2. **Sigmoid 激活函數**：在這種情況下，神經元的輸出由函數`g(x) = 1 / (1 + exp(-x))`指定。 在 TensorFlow 中，有一種方法`tf.sigmoid`，它提供了 Sigmoid 激活。 此函數的范圍在 0 到 1 之間。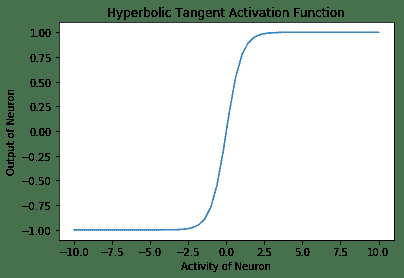形狀上看起來像字母 **S** ，因此名稱為 Sigmoid： ```py # Plotting Sigmoidal Activation function h = np.linspace(-10,10,50) out = tf.sigmoid(h) init = tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) y = sess.run(out) plt.xlabel('Activity of Neuron') plt.ylabel('Output of Neuron') plt.title('Sigmoidal Activation Function') plt.plot(h, y) ``` 以下是以下代碼的輸出：  3. **雙曲正切激活函數**：在數學上，它是`(1 - exp(-2x) / (1 + exp(-2x))`。在形狀上，它類似于 Sigmoid 函數，但是它以 0 為中心，范圍為 -1 至 1。TensorFlow 具有內置函數`tf.tanh`，用于雙曲正切激活函數： ```py # Plotting Hyperbolic Tangent Activation function h = np.linspace(-10,10,50) out = tf.tanh(h) init = tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) y = sess.run(out) plt.xlabel('Activity of Neuron') plt.ylabel('Output of Neuron') plt.title('Hyperbolic Tangent Activation Function') plt.plot(h, y) ``` 以下是上述代碼的輸出：  4. **線性激活函數**：在這種情況下，神經元的輸出與神經元的活動相同。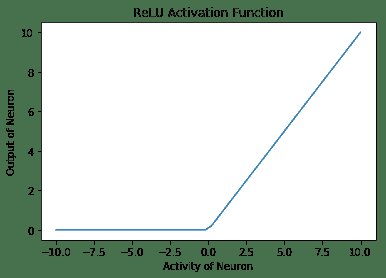 此函數不受任何限制： ```py # Linear Activation Function b = tf.Variable(tf.random_normal([1,1], stddev=2)) w = tf.Variable(tf.random_normal([3,1], stddev=2)) linear_out = tf.matmul(X_in, w) + b init = tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) out = sess.run(linear_out) print(out) ``` 5. **整流線性單元**（**ReLU**）激活函數再次內置在 TensorFlow 庫中。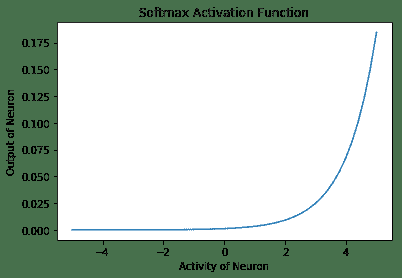 激活函數類似于線性激活函數，但有一個大變化-對于活動的負值，神經元不觸發（零輸出），對于活動的正值，神經元的輸出與給定的活動相同： ```py # Plotting ReLU Activation function h = np.linspace(-10,10,50) out = tf.nn.relu(h) init = tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) y = sess.run(out) plt.xlabel('Activity of Neuron') plt.ylabel('Output of Neuron') plt.title('ReLU Activation Function') plt.plot(h, y) ``` 以下是 ReLu 激活函數的輸出：  6. **Softmax 激活函數**是歸一化的指數函數。 一個神經元的輸出不僅取決于其自身的活動，還取決于該層中存在的所有其他神經元的活動總和。 這樣的一個優點是，它使神經元的輸出保持較小，因此梯度不會爆炸。 數學上，它是`y[i] = exp(x[i]) / ∑j exp(x[j])`： ```py # Plotting Softmax Activation function h = np.linspace(-5,5,50) out = tf.nn.softmax(h) init = tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) y = sess.run(out) plt.xlabel('Activity of Neuron') plt.ylabel('Output of Neuron') plt.title('Softmax Activation Function') plt.plot(h, y) ``` 以下是上述代碼的輸出：  # 工作原理 以下是函數的說明： * **門控激活函數**由 McCulloch Pitts Neuron 和初始感知機使用。 它不可微且在`x = 0`處不連續。 因此，不可能使用此激活函數來使用梯度下降或其變體進行訓練。 * **Sigmoid 激活函數**曾經非常流行。 如果看曲線，它看起來像是閾值激活函數的連續版本。 它具有消失的梯度問題，即，函數的梯度在兩個邊緣附近變為零。 這使得訓練和優化變得困難。 * **雙曲正切激活函數**再次和 Sigmoid 類似，并具有非線性特性。 該函數以零為中心，并且與 Sigmoid 曲線相比具有更陡峭的導數。 像 Sigmoid 一樣，這也遭受消失的梯度問題的困擾。 * **線性激活函數**顧名思義是線性的。 該函數從兩側都是無界的`[-inf, inf]`。 其線性是其主要問題。 線性函數的總和將是線性函數，線性函數的線性函數也將是線性函數。 因此，使用此函數，無法掌握復雜數據集中存在的非線性。 * **ReLU 激活函數**是線性激活函數的整流版本，當在多層中使用時，此整流可以捕獲非線性。 使用 ReLU 的主要優點之一是它導致稀疏激活。 在任何時候，所有具有負活動的神經元都不會放電。 這使網絡在計算方面更輕便。 ReLU 神經元患有垂死的 ReLU 問題，也就是說，不激發的神經元的梯度將變為零，因此將無法進行任何訓練并保持靜止（死）。 盡管存在這個問題，如今的 ReLU 還是隱藏層最常用的激活函數之一。 * **Softmax 激活函數**通常用作輸出層的激活函數。 該函數的范圍為`[0, 1]`。 它用于表示多類分類問題中某類的概率。 所有單元的輸出總和將始終為 1。 # 更多 神經網絡已用于各種任務。 這些任務可以大致分為兩類：函數逼近（回歸）和分類。 根據手頭的任務，一個激活函數可能會優于另一個。 通常，最好將 ReLU 神經元用于隱藏層。 對于分類任務，softmax 通常是更好的選擇，對于回歸問題，最好使用 Sigmoid 或雙曲正切。 # 另見 * [該鏈接提供了 TensorFlow 中定義的激活函數及其使用方法的詳細信息](https://www.tensorflow.org/versions/r0.12/api_docs/python/nn/activation_functions_) * [關于激活函數的不錯總結](https://en.wikipedia.org/wiki/Activation_function) # 單層感知機 簡單的感知機是單層神經網絡。 它使用閾值激活函數，并且正如 Marvin Minsky 論文所證明的那樣，只能解決線性可分離的問題。 盡管這將單層感知機的應用限制為僅是線性可分離的問題，但看到它學習仍然總是令人驚奇。 # 準備 由于感知機使用閾值激活函數，因此我們無法使用 TensorFlow 優化器來更新權重。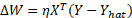 我們將不得不使用權重更新規則：  這是學習率。 為了簡化編程，可以將偏置作為附加權重添加，輸入固定為 +1。 然后，前面的等式可用于同時更新權重和偏差。 # 操作步驟 這是我們處理單層感知機的方法： 1. 導入所需的模塊： ```py import tensorflow as tf import numpy as np ``` 2. 定義要使用的超參數： ```py # Hyper parameters eta = 0.4 # learning rate parameter epsilon = 1e-03 # minimum accepted error max_epochs = 100 # Maximum Epochs ``` 3. 定義`threshold`函數： ```py # Threshold Activation function def threshold (x): cond = tf.less(x, tf.zeros(tf.shape(x), dtype = x.dtype)) out = tf.where(cond, tf.zeros(tf.shape(x)), tf.ones(tf.shape(x))) return out ``` 4. 指定訓練數據。 在此示例中，我們采用三個輸入神經元（`A`，`B`和`C`）并對其進行訓練以學習邏輯`AB + BC`： ```py # Training Data Y = AB + BC, sum of two linear functions. T, F = 1., 0\. X_in = [ [T, T, T, T], [T, T, F, T], [T, F, T, T], [T, F, F, T], [F, T, T, T], [F, T, F, T], [F, F, T, T], [F, F, F, T], ] Y = [ [T], [T], [F], [F], [T], [F], [F], [F] ] ``` 5. 定義要使用的變量，計算圖以計算更新，最后執行計算圖： ```py W = tf.Variable(tf.random_normal([4,1], stddev=2, seed = 0)) h = tf.matmul(X_in, W) Y_hat = threshold(h) error = Y - Y_hat mean_error = tf.reduce_mean(tf.square(error)) dW = eta * tf.matmul(X_in, error, transpose_a=True) train = tf.assign(W, W+dW) init = tf.global_variables_initializer() err = 1 epoch = 0 with tf.Session() as sess: sess.run(init) while err > epsilon and epoch < max_epochs: epoch += 1 err, _ = sess.run([mean_error, train]) print('epoch: {0} mean error: {1}'.format(epoch, err)) print('Training complete') ``` 以下是上述代碼的輸出：  # 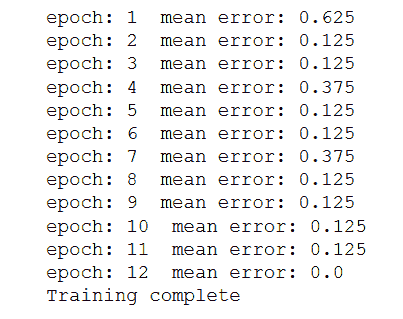更多 如果我們使用 Sigmoid 激活函數代替閾值激活函數，您會怎么辦？ 你猜對了； 首先，我們可以使用 TensorFlow 優化器來更新權重。 其次，網絡的行為類似于邏輯回歸器。 # 反向傳播算法的梯度計算 BPN 算法是神經網絡中研究最多的算法之一。 它用于將誤差從輸出層傳播到隱藏層的神經元，然后將其用于更新權重。 整個學習可以分為兩階段-前向階段和后向階段。 **向前傳遞**：輸入被饋送到網絡，信號從輸入層通過隱藏層傳播，最后傳播到輸出層。 在輸出層，計算誤差和`loss`函數。 **向后傳遞**：在向后傳遞中，首先為輸出層神經元然后為隱藏層神經元計算`loss`函數的梯度。 然后使用梯度更新權重。 重復兩次遍歷，直到達到收斂為止。 # 準備 首先為網絡呈現`M`個訓練對`(X, Y)`，并以`X`作為輸入， `Y`為所需的輸出。 輸入通過激活函數`g(h)`從輸入傳播到隱藏層，直到輸出層。 輸出`Y_hat`是網絡的輸出，誤差為`Y - Y_hat`。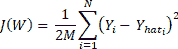 `loss`函數`J(W)`如下：  在此， `i`在輸出層（1 到 N）的所有神經元上變化。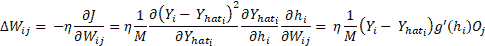 `W[ij]`的權重變化，將輸出層第`i`個神經元連接到隱藏層第`j`個神經元，然后可以使用`J(W)`的梯度并使用鏈規則進行區分來確定隱藏層神經元：  此處， `O[j]`是隱藏層神經元的輸出， `j`和`h`表示活動。 這很容易，但是現在我們如何找到`W[jk]`，它連接第`n`個隱藏層的神經元`k`和第`n+1`隱藏層的神經元`j`？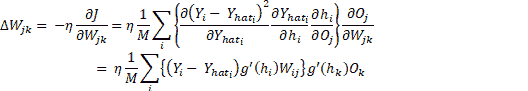流程是相同的，我們將使用`loss`函數的梯度和鏈規則進行微分，但是這次我們將針對`W[jk]`進行計算：  現在方程式就位了，讓我們看看如何在 TensorFlow 中做到這一點。 在本秘籍中，我們使用相同的[舊 MNIST 數據集](http://yann.lecun.com/exdb/mnist/)。 # 操作步驟 現在讓我們開始學習反向傳播算法： 1. 導入模塊： ```py import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data ``` 2. 加載數據集； 我們通過設置`one_hot = True`使用一鍵編碼標簽： ```py mnist = input_data.read_data_sets("MNIST_data/", one_hot=True) ``` 3. 定義超參數和其他常量。 在這里，每個手寫數字的大小為`28 x 28 = 784`像素。 數據集分為 10 類，因為數字可以是 0 到 9 之間的任何數字。這兩個是固定的。 學習率，最大周期數，要訓練的迷你批次的批次大小以及隱藏層中神經元的數量都是超參數。 可以與他們一起玩耍，看看它們如何影響網絡行為： ```py # Data specific constants n_input = 784 # MNIST data input (img shape: 28*28) n_classes = 10 # MNIST total classes (0-9 digits) # Hyperparameters max_epochs = 10000 learning_rate = 0.5 batch_size = 10 seed = 0 n_hidden = 30 # Number of neurons in the hidden layer ``` 4. 我們將需要`sigmoid`函數的導數進行權重更新，因此我們對其進行定義： ```py def sigmaprime(x): return tf.multiply(tf.sigmoid(x), tf.subtract(tf.constant(1.0), tf.sigmoid(x))) ``` 5. 為訓練數據創建占位符： ```py x_in = tf.placeholder(tf.float32, [None, n_input]) y = tf.placeholder(tf.float32, [None, n_classes]) ``` 6. 創建模型： ```py def multilayer_perceptron(x, weights, biases): # Hidden layer with RELU activation h_layer_1 = tf.add(tf.matmul(x, weights['h1']), biases['h1']) out_layer_1 = tf.sigmoid(h_layer_1) # Output layer with linear activation h_out = tf.matmul(out_layer_1, weights['out']) + biases['out'] return tf.sigmoid(h_out), h_out, out_layer_1, h_layer_1 ``` 7. 定義`weights`和`biases`的變量： ```py weights = { 'h1': tf.Variable(tf.random_normal([n_input, n_hidden], seed = seed)), 'out': tf.Variable(tf.random_normal([n_hidden, n_classes], seed = seed)) } biases = { 'h1': tf.Variable(tf.random_normal([1, n_hidden], seed = seed)), 'out': tf.Variable(tf.random_normal([1, n_classes], seed = seed))} ``` 8. 創建用于向前通過，誤差，梯度和更新計算的計算圖： ```py # Forward Pass y_hat, h_2, o_1, h_1 = multilayer_perceptron(x_in, weights, biases) # Error err = y_hat - y # Backward Pass delta_2 = tf.multiply(err, sigmaprime(h_2)) delta_w_2 = tf.matmul(tf.transpose(o_1), delta_2) wtd_error = tf.matmul(delta_2, tf.transpose(weights['out'])) delta_1 = tf.multiply(wtd_error, sigmaprime(h_1)) delta_w_1 = tf.matmul(tf.transpose(x_in), delta_1) eta = tf.constant(learning_rate) # Update weights step = [ tf.assign(weights['h1'],tf.subtract(weights['h1'], tf.multiply(eta, delta_w_1))) , tf.assign(biases['h1'],tf.subtract(biases['h1'], tf.multiply(eta, tf.reduce_mean(delta_1, axis=[0])))) , tf.assign(weights['out'], tf.subtract(weights['out'], tf.multiply(eta, delta_w_2))) , tf.assign(biases['out'], tf.subtract(biases['out'], tf.multiply(eta,tf.reduce_mean(delta_2, axis=[0])))) ] ``` 9. 為`accuracy`定義操作： ```py acct_mat = tf.equal(tf.argmax(y_hat, 1), tf.argmax(y, 1)) accuracy = tf.reduce_sum(tf.cast(acct_mat, tf.float32)) ``` 10. 初始化變量： ```py init = tf.global_variables_initializer() ``` 11. 執行圖： ```py with tf.Session() as sess: sess.run(init) for epoch in range(max_epochs): batch_xs, batch_ys = mnist.train.next_batch(batch_size) sess.run(step, feed_dict = {x_in: batch_xs, y : batch_ys}) if epoch % 1000 == 0: acc_test = sess.run(accuracy, feed_dict = {x_in: mnist.test.images, y : mnist.test.labels}) acc_train = sess.run(accuracy, feed_dict= {x_in: mnist.train.images, y: mnist.train.labels}) print('Epoch: {0} Accuracy Train%: {1} Accuracy Test%: {2}' .format(epoch,acc_train/600,(acc_test/100))) ``` 結果如下：  # 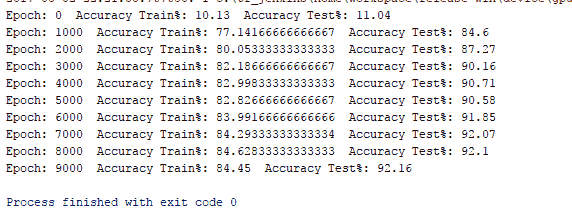工作原理 在這里，我們正在以 10 的批量大小訓練網絡。如果增加它，網絡表現就會下降。 同樣，在測試數據上檢查訓練網絡的準確率； 對其進行測試的測試數據的大小為 1,000。 # 更多 我們的一個隱藏層多層感知機在訓練數據上的準確率為 84.45，在測試數據上的準確率為 92.1。 很好，但還不夠好。 MNIST 數據庫用作機器學習中分類問題的基準。 接下來，我們了解使用 TensorFlow 的內置優化器如何影響網絡表現。 # 另見 * [MNIST 數據庫](http://yann.lecun.com/exdb/mnist/) * [反向傳播算法的簡化解釋](http://neuralnetworksanddeeplearning.com/chap2.html) * [反向傳播算法的另一種直觀解釋](http://cs231n.github.io/optimization-2/) * [關于反向傳播算法的另一種方法，它提供了詳細信息，以及推導以及如何將其應用于不同的 neyworks](https://page.mi.fu-berlin.de/rojas/neural/chapter/K7.pdf) # 使用 MLP 的 MNIST 分類器 TensorFlow 支持自動分化； 我們可以使用 TensorFlow 優化器來計算和應用梯度。 它使用梯度自動更新定義為變量的張量。 在此秘籍中，我們將使用 TensorFlow 優化器來訓練網絡。 # 準備 在反向傳播算法秘籍中，我們定義了層，權重，損耗，梯度，并手動通過梯度進行更新。 為了更好地理解，手動使用方程式進行操作是一個好主意，但是隨著網絡中層數的增加，這可能會非常麻煩。 在本秘籍中，我們將使用強大的 TensorFlow 功能（例如 Contrib（層））來定義神經網絡層，并使用 TensorFlow 自己的優化器來計算和應用梯度。 我們在第 2 章和“回歸”中了解了如何使用不同的 TensorFlow 優化器。 contrib 可用于向神經網絡模型添加各種層，例如添加構建塊。 我們在這里使用的一種方法是`tf.contrib.layers.fully_connected`，在 TensorFlow 文檔中定義如下： ```py fully_connected( inputs, num_outputs, activation_fn=tf.nn.relu, normalizer_fn=None, normalizer_params=None, weights_initializer=initializers.xavier_initializer(), weights_regularizer=None, biases_initializer=tf.zeros_initializer(), biases_regularizer=None, reuse=None, variables_collections=None, outputs_collections=None, trainable=True, scope=None ) ``` 這將添加一個完全連接的層。 `fully_connected` creates a variable called weights, representing a fully connected weight matrix, which is multiplied by the inputs to produce a tensor of hidden units. If a `normalizer_fn` is provided (such as `batch_norm`), it is then applied. Otherwise, if `normalizer_fn` is None and a `biases_initializer` is provided then a biases variable would be created and added to the hidden units. Finally, if `activation_fn` is not None, it is applied to the hidden units as well. # 操作步驟 我們按以下步驟進行： 1. 第一步是更改`loss`函數； 盡管對于分類，最好使用交叉熵`loss`函數。 我們目前繼續**均方誤差**（**MSE**）： ```py loss = tf.reduce_mean(tf.square(y - y_hat, name='loss')) ``` 2. 接下來，我們使用`GradientDescentOptimizer`： ```py optimizer = tf.train.GradientDescentOptimizer(learning_rate= learning_rate) train = optimizer.minimize(loss) ``` 3. 僅通過這兩個更改，對于同一組超參數，測試數據集的準確率僅為 61.3%。 增加`max_epoch`，我們可以提高精度，但這將不是 TensorFlow 功能的有效利用。 4. 這是一個分類問題，因此最好使用交叉熵損失，用于隱藏層的 ReLU 激活函數以及用于輸出層的 softmax。 進行所需的更改，完整代碼如下： ```py import tensorflow as tf import tensorflow.contrib.layers as layers from tensorflow.python import debug as tf_debug # Network Parameters n_hidden = 30 n_classes = 10 n_input = 784 # Hyperparameters batch_size = 200 eta = 0.001 max_epoch = 10 # MNIST input data from tensorflow.examples.tutorials.mnist import input_data mnist = input_data.read_data_sets("/tmp/data/", one_hot=True) def multilayer_perceptron(x): fc1 = layers.fully_connected(x, n_hidden, activation_fn=tf.nn.relu, scope='fc1') #fc2 = layers.fully_connected(fc1, 256, activation_fn=tf.nn.relu, scope='fc2') out = layers.fully_connected(fc1, n_classes, activation_fn=None, scope='out') return out # build model, loss, and train op x = tf.placeholder(tf.float32, [None, n_input], name='placeholder_x') y = tf.placeholder(tf.float32, [None, n_classes], name='placeholder_y') y_hat = multilayer_perceptron(x) loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=y_hat, labels=y)) train = tf.train.AdamOptimizer(learning_rate= eta).minimize(loss) init = tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) for epoch in range(10): epoch_loss = 0.0 batch_steps = int(mnist.train.num_examples / batch_size) for i in range(batch_steps): batch_x, batch_y = mnist.train.next_batch(batch_size) _, c = sess.run([train, loss], feed_dict={x: batch_x, y: batch_y}) epoch_loss += c / batch_steps print ('Epoch %02d, Loss = %.6f' % (epoch, epoch_loss)) # Test model correct_prediction = tf.equal(tf.argmax(y_hat, 1), tf.argmax(y, 1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) print ("Accuracy%:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels})) ``` # 工作原理 改進的 MNIST MLP 分類器在測試數據集上的準確率達到了 96%，只有一個隱藏層并且在 10 個周期內。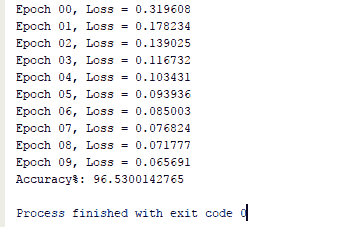 僅在幾行代碼中我們就獲得了約 96% 的準確率，這就是 TensorFlow 的強大功能：  # 使用 MLP 預測波士頓房價的函數近似 [Hornik 等人的工作](http://www.cs.cmu.edu/~bhiksha/courses/deeplearning/Fall.2016/notes/Sonia_Hornik.pdf)證明了以下： "multilayer feedforward networks with as few as one hidden layer are indeed capable of universal approximation in a very precise and satisfactory sense." 在本秘籍中，我們將向您展示如何使用 MLP 進行函數逼近； 具體來說，我們將預測波士頓的房價。 我們已經熟悉了數據集； 在第 2 章，“回歸”中，我們使用回歸技術進行房價預測，現在我們將使用 MLP 進行相同的操作。 # 準備 對于函數逼近，`loss`函數應為 MSE。 輸入應該標準化，而隱藏層可以是 ReLU，而輸出層則最好是 Sigmoid 。 # 操作步驟 這是我們從使用 MLP 進行函數逼近開始的方法： 1. 導入所需的模塊-`sklearn`用于數據集，預處理數據，并將其拆分為訓練和測試； Pandas 用于了解數據集； `matplotlib`和`seaborn`用于可視化： ```py import tensorflow as tf import tensorflow.contrib.layers as layers from sklearn import datasets import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.preprocessing import MinMaxScaler import pandas as pd import seaborn as sns %matplotlib inline ``` 2. 加載數據集并創建一個 Pandas 數據幀以了解數據： ```py # Data boston = datasets.load_boston() df = pd.DataFrame(boston.data, columns=boston.feature_names) df['target'] = boston.target ``` 3. 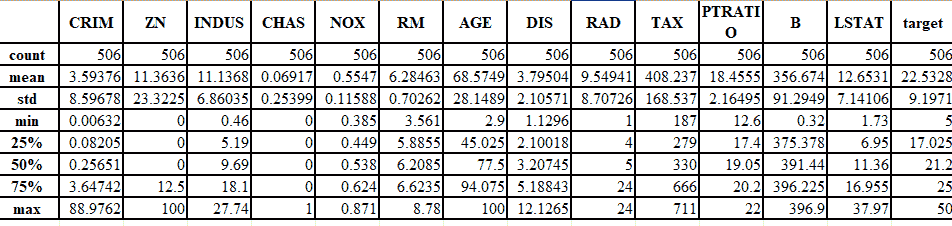讓我們獲取有關數據的一些詳細信息： ```py #Understanding Data df.describe() ``` 下圖很好地說明了這一概念：  4. 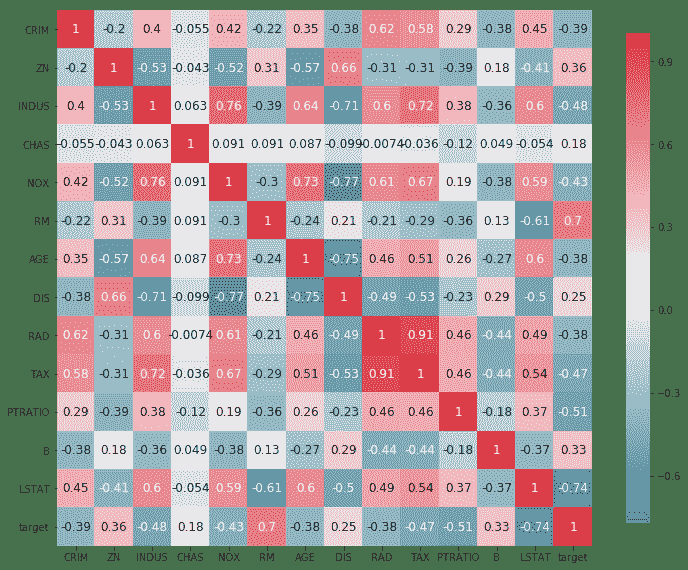查找不同輸入特征和目標之間的關聯： ```py # Plotting correlation color map _ , ax = plt.subplots( figsize =( 12 , 10 ) ) corr = df.corr(method='pearson') cmap = sns.diverging_palette( 220 , 10 , as_cmap = True ) _ = sns.heatmap( corr, cmap = cmap, square=True, cbar_kws={ 'shrink' : .9 }, ax=ax, annot = True, annot_kws = { 'fontsize' : 12 }) ``` 以下是上述代碼的輸出：  5. 從前面的代碼中，我們可以看到`RM`，`PTRATIO`和`LSTAT`這三個參數的相關性在大小上大于 0.5。 我們選擇它們進行訓練。 將數據集拆分為訓練和測試數據集。 我們還使用`MinMaxScaler`歸一化我們的數據集。 需要注意的一個重要變化是，由于我們的神經網絡使用了 Sigmoid 激活函數（Sigmoid 的輸出只能在 0-1 之間），因此我們也必須將目標值`Y`標準化： ```py # Create Test Train Split X_train, X_test, y_train, y_test = train_test_split(df [['RM', 'LSTAT', 'PTRATIO']], df[['target']], test_size=0.3, random_state=0) # Normalize data X_train = MinMaxScaler().fit_transform(X_train) y_train = MinMaxScaler().fit_transform(y_train) X_test = MinMaxScaler().fit_transform(X_test) y_test = MinMaxScaler().fit_transform(y_test) ``` 6. 定義常量和超參數： ```py #Network Parameters m = len(X_train) n = 3 # Number of features n_hidden = 20 # Number of hidden neurons # Hyperparameters batch_size = 200 eta = 0.01 max_epoch = 1000 ``` 7. 創建具有一個隱藏層的多層感知機模型： ```py def multilayer_perceptron(x): fc1 = layers.fully_connected(x, n_hidden, activation_fn=tf.nn.relu, scope='fc1') out = layers.fully_connected(fc1, 1, activation_fn=tf.sigmoid, scope='out') return out ``` 8. 聲明訓練數據的占位符，并定義損失和優化器： ```py # build model, loss, and train op x = tf.placeholder(tf.float32, name='X', shape=[m,n]) y = tf.placeholder(tf.float32, name='Y') y_hat = multilayer_perceptron(x) correct_prediction = tf.square(y - y_hat) mse = tf.reduce_mean(tf.cast(correct_prediction, "float")) train = tf.train.AdamOptimizer(learning_rate= eta).minimize(mse) init = tf.global_variables_initializer() ``` 9. 執行計算圖： ```py # Computation Graph with tf.Session() as sess: # Initialize variables sess.run(init) writer = tf.summary.FileWriter('graphs', sess.graph) # train the model for 100 epcohs for i in range(max_epoch): _, l, p = sess.run([train, loss, y_hat], feed_dict={x: X_train, y: y_train}) if i%100 == 0: print('Epoch {0}: Loss {1}'.format(i, l)) print("Training Done") print("Optimization Finished!") # Test model correct_prediction = tf.square(y - y_hat) # Calculate accuracy accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print(" Mean Error:", accuracy.eval({x: X_train, y: y_train})) plt.scatter(y_train, p) writer.close() ``` # 工作原理 該模型只有一個隱藏層，因此可以預測訓練數據集的價格，平均誤差為 0.0071。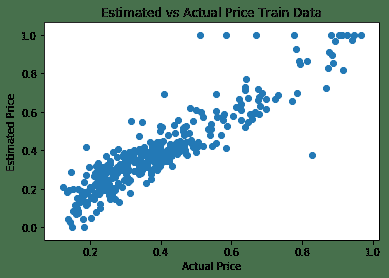 下圖顯示了房屋的估計價格與實際價格之間的關系：  # 更多 在這里，我們使用 TensorFlow ops Layers（Contrib）來構建神經網絡層。 由于避免了分別聲明每一層的權重和偏差，因此使我們的工作稍微容易一些。 如果我們使用像 Keras 這樣的 API，可以進一步簡化工作。 這是在 Keras 中使用 TensorFlow 作為后端的相同代碼： ```py #Network Parameters m = len(X_train) n = 3 # Number of features n_hidden = 20 # Number of hidden neurons # Hyperparameters batch = 20 eta = 0.01 max_epoch = 100 # Build Model model = Sequential() model.add(Dense(n_hidden, model.add(Dense(1, activation='sigmoid')) model.summary() # Summarize the model #Compile model model.compile(loss='mean_squared_error', optimizer='adam') #Fit the model model.fit(X_train, y_train, validation_data=(X_test, y_test),epochs=max_epoch, batch_size=batch, verbose=1) #Predict the values and calculate RMSE and R2 score y_test_pred = model.predict(X_test) y_train_pred = model.predict(X_train) r2 = r2_score( y_test, y_test_pred ) rmse = mean_squared_error( y_test, y_test_pred ) print( "Performance Metrics R2 : {0:f}, RMSE : {1:f}".format( r2, rmse ) ) ``` 前面的代碼在預測值和實際值之間給出了以下結果。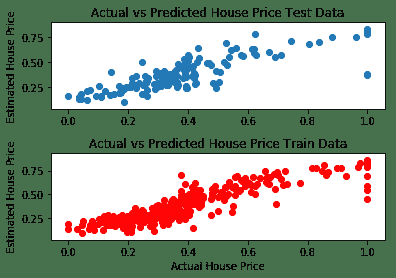 我們可以看到，通過消除異常值可以改善結果（某些房屋的最高價格與其他參數無關，位于最右邊的點）：  # 調整超參數 正如您現在必須已經觀察到的那樣，神經網絡的表現在很大程度上取決于超參數。 因此，重要的是要了解這些參數如何影響網絡。 超參數的常見示例是學習率，正則化器，正則化系數，隱藏層的尺寸，初始權重值，甚至是為優化權重和偏差而選擇的優化器。 # 操作步驟 這是我們進行秘籍的方法： 1. 調整超參數的第一步是構建模型。 完全按照我們以前的方式在 TensorFlow 中構建模型。 2. 添加一種將模型保存在`model_file`中的方法。 在 TensorFlow 中，可以使用`Saver`對象完成此操作。 然后將其保存在會話中： ```py ... saver = tf.train.Saver() ... with tf.Session() as sess: ... #Do the training steps ... save_path = saver.save(sess, "/tmp/model.ckpt") print("Model saved in file: %s" % save_path) ``` 3. 接下來，確定要調整的超參數。 4. 為超參數選擇可能的值。 在這里，您可以進行隨機選擇，等距選擇或手動選擇。 這三個分別稱為隨機搜索，網格搜索或用于優化超參數的手動搜索。 例如，這是針對學習率的： ```py # Random Choice: generate 5 random values of learning rate # lying between 0 and 1 learning_rate = #Grid Search: generate 5 values starting from 0, separated by # 0.2 learning_rate = [i for i in np.arange(0,1,0.2)] #Manual Search: give any values you seem plausible manually learning_rate = [0.5, 0.6, 0.32, 0.7, 0.01] ``` 5. 我們選擇對我們選擇的`loss`函數具有最佳響應的參數。 因此，我們可以在開始時將`loss`函數的最大值定義為`best_loss`（在精度的情況下，您將從模型中選擇所需的最小精度）： ```py best_loss = 2 # It can be any number, but it would be better if you keep it same as the loss you achieved from your base model defined in steps 1 and 2 ``` 6. 將模型包裝在`for`循環中以提高學習率； 然后保存任何可以更好地估計損失的模型： ```py ... # Load and preprocess data ... # Hyperparameters Tuning epochs = [50, 60, 70] batches = [5, 10, 20] rmse_min = 0.04 for epoch in epochs: for batch in batches: model = get_model() model.compile(loss='mean_squared_error', optimizer='adam') model.fit(X_train, y_train, validation_data=(X_test, y_test),epochs=epoch, batch_size=batch, verbose=1) y_test_pred = model.predict(X_test) rmse = mean_squared_error( y_test, y_test_pred ) if rmse < rmse_min: rmse_min = rmse # serialize model to JSON model_json = model.to_json() with open("model.json", "w") as json_file: json_file.write(model_json) # serialize weights to HDF5 model.save_weights("model.hdf5") print("Saved model to disk") ``` # 更多 還有另一種稱為**貝葉斯優化**的方法，該方法也可以用于調整超參數。 在其中，我們定義了一個采集函數以及一個高斯過程。 高斯過程使用一組先前評估的參數以及由此產生的精度來假設大約未觀測到的參數。 使用此信息的采集功能建議使用下一組參數。 有一個包裝程序甚至可用于[基于梯度的超參數優化](https://github.com/lucfra/RFHO)。 # 另見 * [兩個用于超級參數優化的出色開源包的很好介紹：Hyperopt 和 scikit-optimize](https://roamanalytics.com/2016/09/15/optimizing-the-hyperparameter-of-which-hyperparameter-optimizer-to-use/) * [另一個有關 Hyperopt 的內容](http://fastml.com/optimizing-hyperparams-with-hyperopt/) * [Bengio 和其他人撰寫的有關超參數優化各種算法的詳細論文](https://papers.nips.cc/paper/4443-algorithms-for-hyper-parameter-optimization.pdf) # 更高級別的 API -- Keras Keras 是將 TensorFlow 作為后端使用的高級 API。 向其添加層就像添加一行代碼一樣容易。 在建立模型架構之后，您可以使用一行代碼來編譯和擬合模型。 以后，它可以用于預測。 變量，占位符甚至會話的聲明均由 API 管理。 # 操作步驟 我們對 Keras 進行如下操作： 1. 第一步，我們定義模型的類型。 Keras 提供了兩種類型的模型：順序模型 API 和模型類 API。 Keras 提供了各種類型的神經網絡層： ```py # Import the model and layers needed from keras.model import Sequential from keras.layers import Dense model = Sequential() ``` 2. 借助`model.add()`將層添加到模型中。 Keras 為密集連接的神經網絡`layer Dense(units, activation=None, use_bias=True, kernel_initializer='glorot_uniform', bias_initializer='zeros', kernel_regularizer=None, bias_regularizer=None, activity_regularizer=None, kernel_constraint=None, bias_constraint=None)`提供了一個密集層的選項。 根據 Keras 文檔： Dense implements the operation: `output = activation(dot(input, kernel) + bias)` where activation is the element-wise activation function passed as the activation argument, kernel is a weights matrix created by the layer, and bias is a bias vector created by the layer (only applicable if `use_bias` is `True`). 3. 我們可以使用它來添加任意數量的層，每個隱藏的層都由上一層提供。 我們只需要為第一層指定輸入尺寸： ```py #This will add a fully connected neural network layer with 32 neurons, each taking 13 inputs, and with activation function ReLU mode.add(Dense(32, input_dim=13, activation='relu')) )) model.add(10, activation='sigmoid') ``` 4. 定義模型后，我們需要選擇`loss`函數和優化器。 Keras 提供了多種`loss_functions`：`mean_squared_error`，`mean_absolute_error`，`mean_absolute_percentage_error`，`categorical_crossentropy`； 和優化程序：SGD，RMSprop，Adagrad，Adadelta，Adam 等。 決定了這兩個條件后，我們可以使用`compile(self, optimizer, loss, metrics=None, sample_weight_mode=None)`配置學習過程： ```py model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy']) ``` 5. 接下來，使用`fit`方法訓練模型： ```py model.fit(data, labels, epochs=10, batch_size=32) ``` 6. 最后，可以借助`predict`方法`predict(self, x, batch_size=32, verbose=0)`進行預測： ```py model.predict(test_data, batch_size=10) ``` # 更多 Keras 提供了添加卷積層，池化層，循環層甚至本地連接層的選項。 [Keras 文檔](https://keras.io/models/sequential/)中提供了每種方法的詳細說明。 # 另見 ```py McCulloch, Warren S., and Walter Pitts. A logical calculus of the ideas immanent in nervous activity The bulletin of mathematical biophysics 5.4 (1943): 115-133. http://vordenker.de/ggphilosophy/mcculloch_a-logical-calculus.pdf Rosenblatt, Frank (1957), The Perceptron--a perceiving and recognizing automaton. Report 85-460-1, Cornell Aeronautical Laboratory. https://blogs.umass.edu/brain-wars/files/2016/03/rosenblatt-1957.pdf The Thinking Machine, CBS Broadcast https://www.youtube.com/watch?v=jPHUlQiwD9Y ```