# 二、深度學習和卷積神經網絡 在開始本章之前，我們需要討論一下 AI 和**機器學習**（**ML**）以及這兩個組件如何組合在一起。 術語“人工”是指不真實或自然的事物，而“智能”是指能夠理解，學習或能夠解決問題的事物（在極端情況下，具有自我意識）。 正式地，人工智能研究始于 1956 年的達特茅斯會議，其中定義了 AI 及其使命。 在接下來的幾年中，每個人都很樂觀，因為機器能夠解決代數問題和學習英語，并且在 1972 年制造了第一臺機器人。但是在 1970 年代，由于過分的承諾但交付不足，出現了所謂的 AI 冬季，人工智能研究有限且資金不足。 此后，盡管 AI 通過專家系統重生，但可以顯示人類水平的分析技能。 之后，第二次 AI 冬季機器學習在 1990 年代被認可為一個單獨的領域，當時概率理論和統計學開始得到利用。 計算能力的提高和解決特定問題的決心促使 IBM 的深藍的發展在 1997 年擊敗了國際象棋冠軍。 迅速發展，時下的 AI 領域涵蓋了許多領域，包括機器學習，計算機視覺，自然語言處理，計劃調度和優化，推理/專家系統和機器人技術。 在過去的 10 年中，我們目睹了機器學習和一般 AI 的強大功能。 主要感謝深度學習。 在本章中，我們將涵蓋以下主題： * AI 和 ML 概念的一般說明 * 人工神經網絡和深度學習 * **卷積神經網絡**（**CNN**）及其主要構建模塊 * 使用 TensorFlow 構建 CNN 模型以識別數字圖像 * Tensorboard 簡介 # AI 和 ML 就本書而言，將**人工智能**（**AI**）視為計算機科學領域，負責制造可解決特定問題的智能體（軟件/機器人）。 在這種情況下，“智能”表示智能體是靈活的，并且它通過傳感器感知環境，并將采取使自身在某個特定目標成功的機會最大化的措施。 我們希望 AI 最大化名為**期望效用**的東西，或者通過執行動作獲得某種滿足的概率。 一個簡單易懂的例子是上學，您將最大程度地獲得工作的期望效用。 人工智能渴望取代在完成繁瑣的日常任務中涉及的易于出錯的人類智能。 AI 旨在模仿（以及智能智能體應該具有）的人類智能的一些主要組成部分是： * **自然語言處理**（**NLP**）：能夠理解口頭或書面人類語言，并能自然回答問題。 NLP 的一些示例任務包括自動旁白，機器翻譯或文本摘要。 * **知識和推理**：開發并維護智能體周圍世界的最新知識。 遵循人類推理和決策來解決特定問題并對環境的變化做出反應。 * **規劃和解決問題的方法**：對可能采取的措施進行預測，并選擇能最大化預期效用的方案，換句話說，為該情況選擇最佳措施。 * **感知**：智能體程序所配備的傳感器向其提供有關智能體程序所處世界的信息。這些傳感器可以像紅外傳感器一樣簡單，也可以像語音識別麥克風那樣復雜。 或相機以實現機器視覺。 * **學習**：要使智能體開發世界知識，它必須使用感知來通過觀察來學習。 學習是一種知識獲取的方法，可用于推理和制定決策。 AI 的無需處理某些明確編程即可處理從數據中學習算法的子字段，稱為機器學習。 ML 使用諸如統計分析，概率模型，決策樹和神經網絡之類的*工具*來有效地處理大量數據，而不是人類。 例如，讓我們考慮以下手勢識別問題。 在此示例中，我們希望我們的機器識別正在顯示的手勢。 系統的輸入是手部圖像，如下圖所示，輸出是它們所代表的數字。 解決該問題的系統需要使用視覺形式的感知。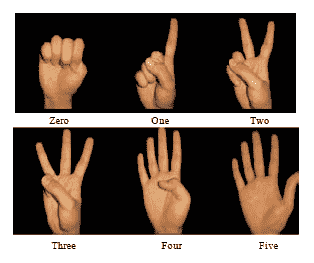  僅將原始圖像作為輸入輸入到我們的機器將不會產生合理的結果。 因此，應對圖像進行預處理以提取某種可解釋的抽象。 在我們的特定情況下，最簡單的方法是根據顏色對手進行分割，然后進行垂直投影，將`x`軸上的非零值相加。 如果圖像的寬度為 100 像素，則垂直投影將形成一個向量，該向量長 100 個元素（100 維），并且在展開的手指位置具有最高的值。 我們可以將提取的任何特征向量稱為**特征向量**。 假設對于我們的手部數據，我們有 1000 張不同的圖像，現在我們已經對其進行處理以提取每個圖像的特征向量。 在機器學習階段，所有特征向量都將被提供給創建模型的機器學習系統。 我們希望該模型能夠推廣并能夠預測未經過系統訓練的任何未來圖像的數字。 ML 系統的組成部分是評估。 在評估模型時，我們會看到模型在特定任務中的表現。 在我們的示例中，我們將研究它可以多么準確地從圖像中預測數字。 90% 的準確率意味著正確預測了 100 張給定圖像中的 90 張。 在接下來的章節中，我們將更詳細地討論機器訓練和評估過程。 # ML 的類型 機器學習問題可以分為三大類，具體取決于我們可以使用哪種數據以及我們想要完成什么： **監督學習**：我們可以使用輸入和所需的輸出或標簽。 手勢分類是一種有監督學習問題的示例，其中為我們提供了手勢和相應標簽的圖像。 我們想要創建一個模型，該模型能夠在輸入手形圖像的情況下輸出正確的標簽。 監督技術包括 SVM，LDA，神經網絡，CNN，KNN，決策樹等。 **無監督學習**：只有輸入可用，沒有標簽，我們不一定知道我們想要模型做什么。 例如，如果我們得到一個包含手的圖片但沒有標簽的大型數據集。 在這種情況下，我們可能知道數據中存在某些結構或關系，但是我們將其留給算法來嘗試在我們的數據中找到它們。 我們可能希望我們的算法在數據中找到相似手勢的簇，因此我們不必手動標記它們。 無監督學習的另一種用途是找到方法，以減少我們正在使用的數據的維度，這又是通過找到數據中的重要特征并丟棄不重要的特征來實現的。 無監督技術包括 PCA，t-SNE，K 均值，自編碼器，深度自編碼器等。 下圖說明了分類和聚類之間的區別（當我們需要在非監督數據上查找結構時）。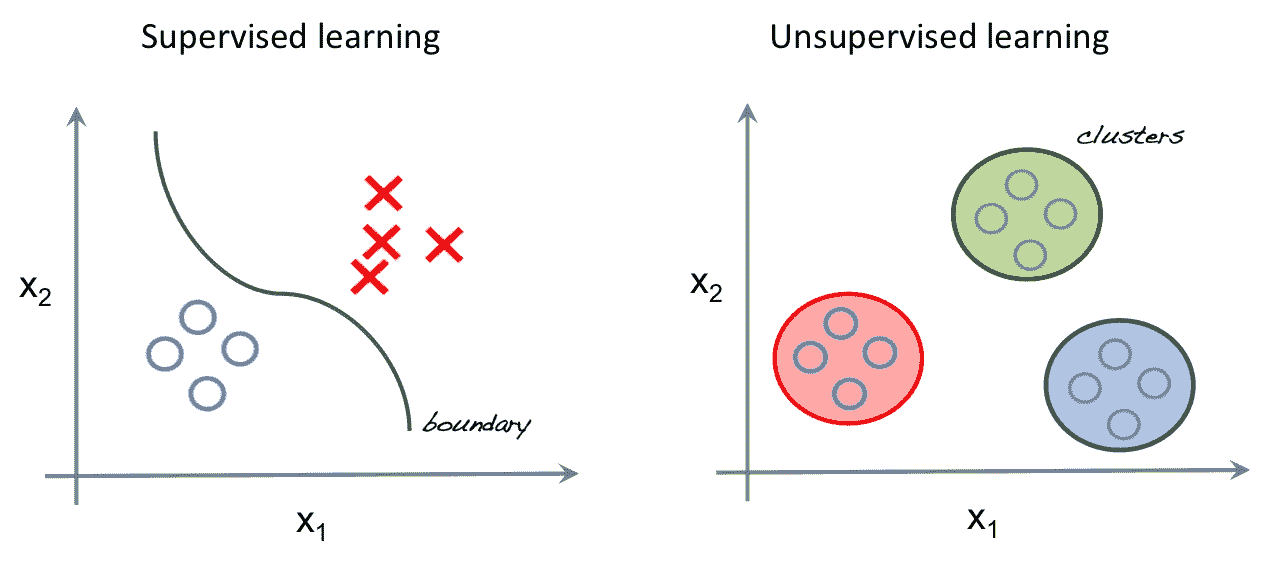  **強化學習**：第三種是關于訓練智能體在環境中執行某些操作的全部。 我們知道理想的結果，但不知道如何實現。 我們沒有給數據加標簽，而是給智能體提供反饋，告訴它完成任務的好壞。 強化學習超出了本書的范圍。 # 新舊機器學習 ML 工程師可能會遵循的典型流程來開發預測模型，如下所示： 1. 收集數據 2. 從數據中提取相關特征 3. 選擇 ML 架構（CNN，ANN，SVM，決策樹等） 4. 訓練模型 5. 評估模型并重復步驟 3 至 5，直到找到滿意的解決方案 6. 在現場測試模型 如前一節所述，機器學習的思想是擁有足夠靈活的算法來學習數據背后的基礎過程。 可以這么說，許多經典的 ML 方法不夠強大，無法直接從數據中學習。 他們需要在使用這些算法之前以某種方式準備數據。 我們之前曾簡要提到過，但是準備數據的過程通常稱為特征提取，其中一些專家會過濾掉我們認為與其基礎過程有關的所有數據細節。 此過程使所選分類器的分類問題更加容易，因為它不必處理數據中不相關的變量，否則這些變量可能會顯得很重要。 ML 的新型深度學習方法具有的最酷的功能是，它們不需要（或需要更少）特征提取階段。 相反，使用足夠大的數據集，模型本身就能夠直接從數據本身中學習代表數據的最佳特征！ 這些新方法的示例如下： * 深度 CNN * 深度自編碼器 * **生成對抗網絡**（**GAN**） 所有這些方法都是深度學習過程的一部分，在該過程中，大量數據暴露于多層神經網絡。 但是，這些新方法的好處是有代價的。 所有這些新算法都需要更多的計算資源（CPU 和 GPU），并且比傳統方法需要更長的訓練時間。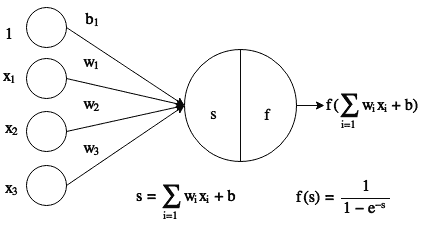 # 人工神經網絡 **人工神經網絡**（**ANN**）受存在于我們大腦中的神經元生物網絡的啟發非常模糊，它由一組名為**人工神經元**的單元組成， 分為以下三種類型的層： * 輸入層 * 隱藏層 * 輸出層 基本的人工神經元通過計算輸入及其內部*權重*之間的點積來工作（參見下圖），然后將結果傳遞給非線性激活函數`f`（在此示例中是 Sigmoid）。 然后將這些人工神經元連接在一起以形成網絡。 在訓練該網絡期間，目標是找到合適的權重集，這些權重將有助于我們希望網絡執行的任何任務：  接下來，我們有一個 2 層前饋人工神經網絡的示例。 想象一下，神經元之間的聯系就是訓練過程中將學習的權重。 在此示例中，層`L1`將是輸入層，`L2`隱藏層，而`L3`將是輸出層。 按照慣例，在計算層數時，我們僅包括權重可學習的層； 因此，我們不包括輸入層。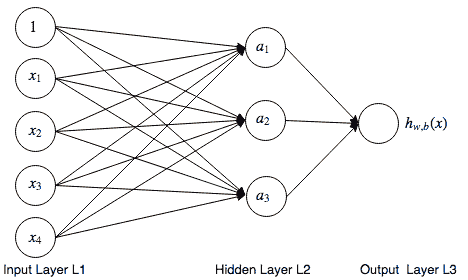 這就是為什么它只是一個 2 層網絡：  一層以上的神經網絡是非線性假設的示例，在該模型中，模型可以學習比線性分類器更復雜的關系。 實際上，它們實際上是通用逼近器，能夠逼近任何連續函數。 # 激活函數 為了使 ANN 模型能夠解決更復雜的問題，我們需要在神經元點積之后添加一個非線性塊。 然后，如果將這些非線性層級聯起來，它將使網絡將不同的概念組合在一起，從而使復雜的問題更易于解決。 在神經元中使用非線性激活非常重要。 如果我們不使用非線性激活函數，那么無論我們層疊了多少層，我們都只會擁有行為類似于線性模型的東西。 這是因為線性函數的任何線性組合都會分解為線性函數。 我們的神經元可以使用多種不同的激活函數，此處顯示了一些； 唯一重要的是函數是非線性的。 每個激活函數都有其自身的優點和缺點。 歷史上，神經網絡選擇的激活函數是 Sigmoid 和 *TanH*。 但是，這些功能對于可靠地訓練神經網絡不利，因為它們具有不希望的特性，即它們的值在任一端都飽和。 這將導致這些點處的梯度為零，我們將在后面找到，并且在訓練神經網絡時不是一件好事。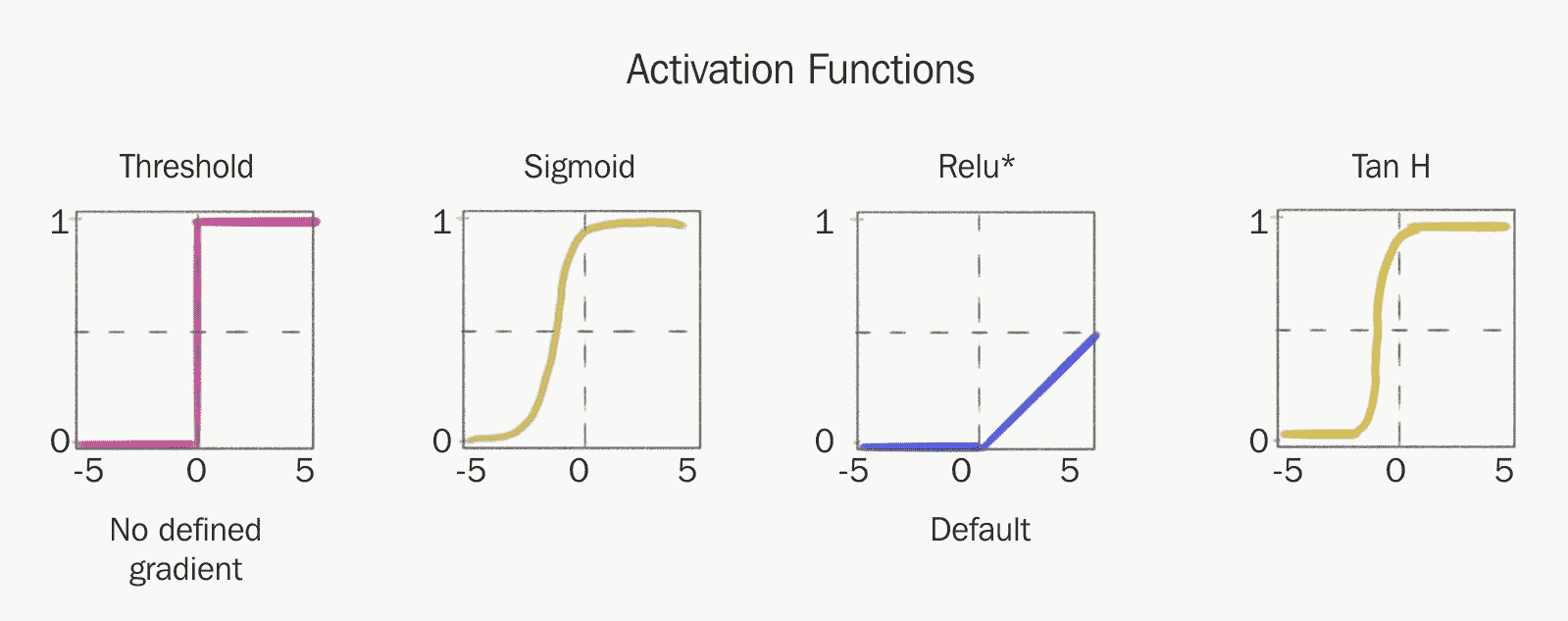  結果，更流行的激活函數之一是 ReLU 激活或**整流線性單元**。 ReLU 只是`max(x, 0)`，輸入和 0 之間的最大運算。 它具有理想的特性，即梯度（至少在一端）不會變為零，這極大地有助于神經網絡訓練的收斂速度。 該激活函數用于幫助訓練深層的 CNN 之后，變得越來越流行。 它的簡單性和有效性使其成為通常使用的激活函數。 # XOR 問題 為了解釋深度在 ANN 中的重要性，我們將研究一個 ANN 能夠解決的非常簡單的問題，因為它具有多個層。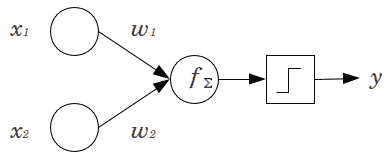 在使用人工神經元的早期，人們并不像我們在人工神經網絡中那樣將各層級聯在一起，因此我們最終得到了一個稱為感知器的單層：  感知器實際上只是輸入和一組學習的權重之間的點積，這意味著它實際上只是線性分類器。 大約在第一個 AI 冬季，人們意識到了感知器的弱點。 由于它只是線性分類器，因此無法解決簡單的非線性分類問題，例如布爾異或（XOR）問題。 為了解決這個問題，我們需要更深入地研究。 在此圖中，我們看到了一些不同的布爾邏輯問題。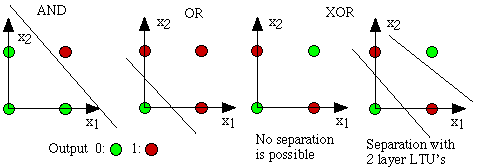 線性分類器可以解決 AND 和 OR 問題，但不能解決 XOR：  這使人們有了將使用非線性激活的神經元層級聯在一起的想法。 一層可以根據上一層的輸出來創建非線性概念。 這種“概念的組合”使網絡變得更強大，并能代表更困難的功能，因此，它們能夠解決非線性分類問題。 # 訓練神經網絡 那么，我們該如何在神經網絡中設置權重和偏差的值，從而最好地解決我們的問題呢？ 好吧，這是在訓練階段完成的。 在此階段中，我們希望使神經網絡從訓練數據集中“學習”。 訓練數據集由一組輸入（通常表示為 X）以及相應的所需輸出或標簽（通常表示為 Y）組成。 當我們說網絡學習時，所發生的就是網絡參數被更新，網絡應該能夠為訓練數據集中的每個 X 輸出正確的 Y。 期望的是，在對網絡進行訓練之后，它將能夠針對訓練期間未看到的新輸入進行概括并表現良好。 但是，為了做到這一點，您必須有一個足夠具有代表性的數據集，以捕獲要輸出的內容。 例如，如果要分類汽車，則需要具有不同類型，顏色，照度等的數據集。 通常，當我們沒有足夠的數據或者我們的模型不夠復雜以至于無法捕獲數據的復雜性時，就會出現訓練機器學習模型的一個常見錯誤。 這些錯誤可能導致過擬合和欠擬合的問題。 在以后的章節中，您將學習如何在實踐中處理這些問題。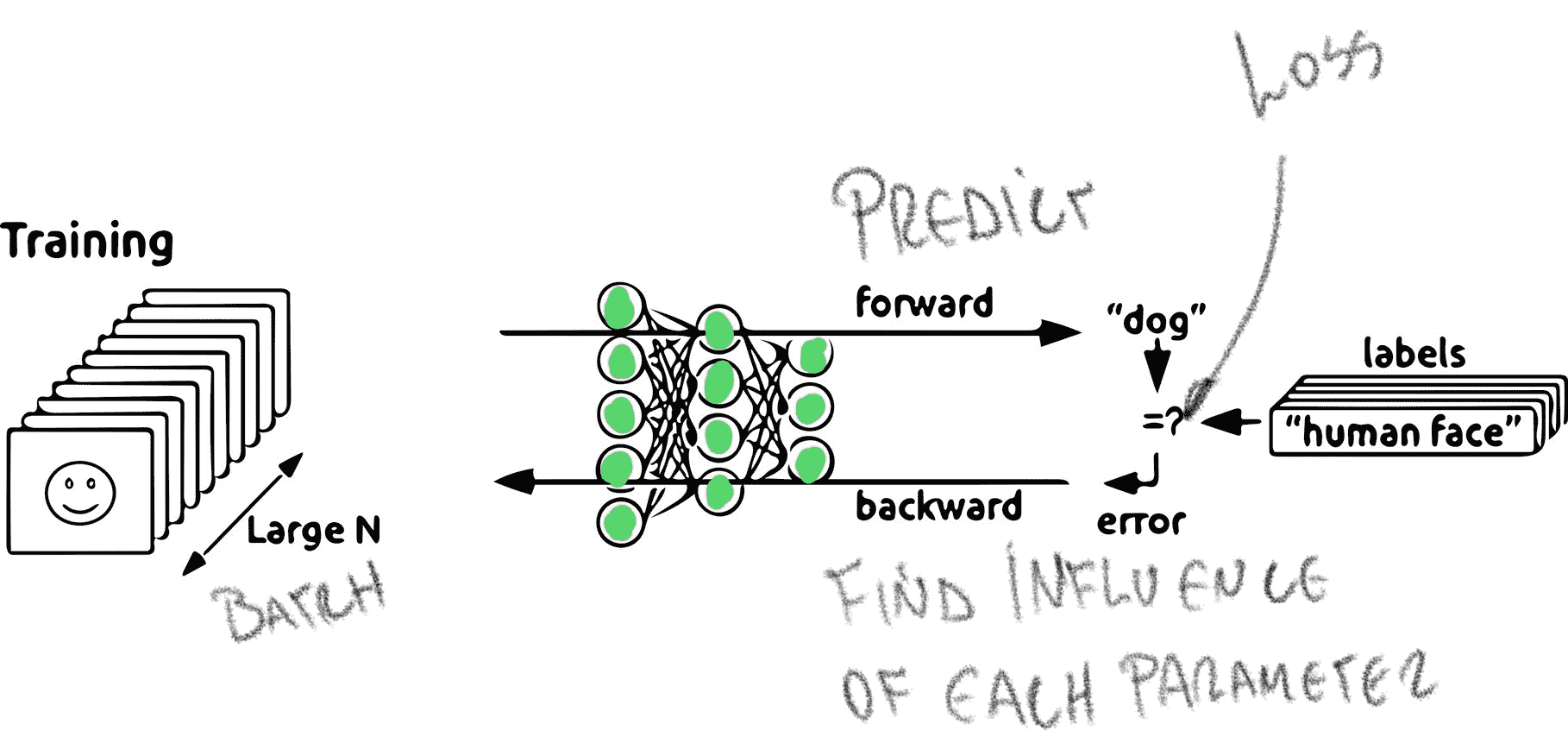 在訓練期間，*以兩種不同的模式執行網絡*： * **正向傳播**：我們通過網絡向前工作，為數據集中的當前給定輸入生成輸出結果。 然后評估損失函數，該函數告訴我們網絡在預測正確輸出方面的表現如何。 * **反向傳播**：我們通過網絡進行反向計算，計算每個權重對產生網絡電流損失的影響。 此圖顯示了訓練時網絡運行的兩種不同方式。  當前，使神經網絡“學習”的主力軍是與基于梯度的優化器（例如梯度下降）結合的反向傳播算法。 反向傳播用于計算梯度，該梯度告訴我們每個權重對產生電流損失有什么影響。 找到梯度后，可以使用諸如梯度下降之類的優化技術來更新權重，以使損失函數的值最小化。 謹在最后一句話：TensorFlow，PyTorch，Caffe 或 CNTK 之類的 ML 庫將提供反向傳播，優化器以及表示和訓練神經網絡所需的所有其他功能，而無需您自己重寫所有這些代碼。 # 反向傳播和鏈式規則 反向傳播算法實際上只是微積分中可信賴鏈規則的一個示例。 它說明了如何找到某個輸入對由多個功能組成的系統的影響。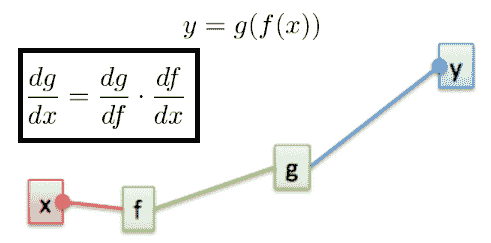 因此，例如在下圖中，如果您想知道`x`對函數`g`的影響，我們只需將`f`對`g`的影響乘以`x`對`f`的影響：  同樣，這意味著如果我們想實現自己的深度學習庫，則需要定義層的正常計算（正向傳播）以及此計算塊相對于其輸入的影響（導數）。 下面我們給出一些常見的神經網絡操作及其梯度。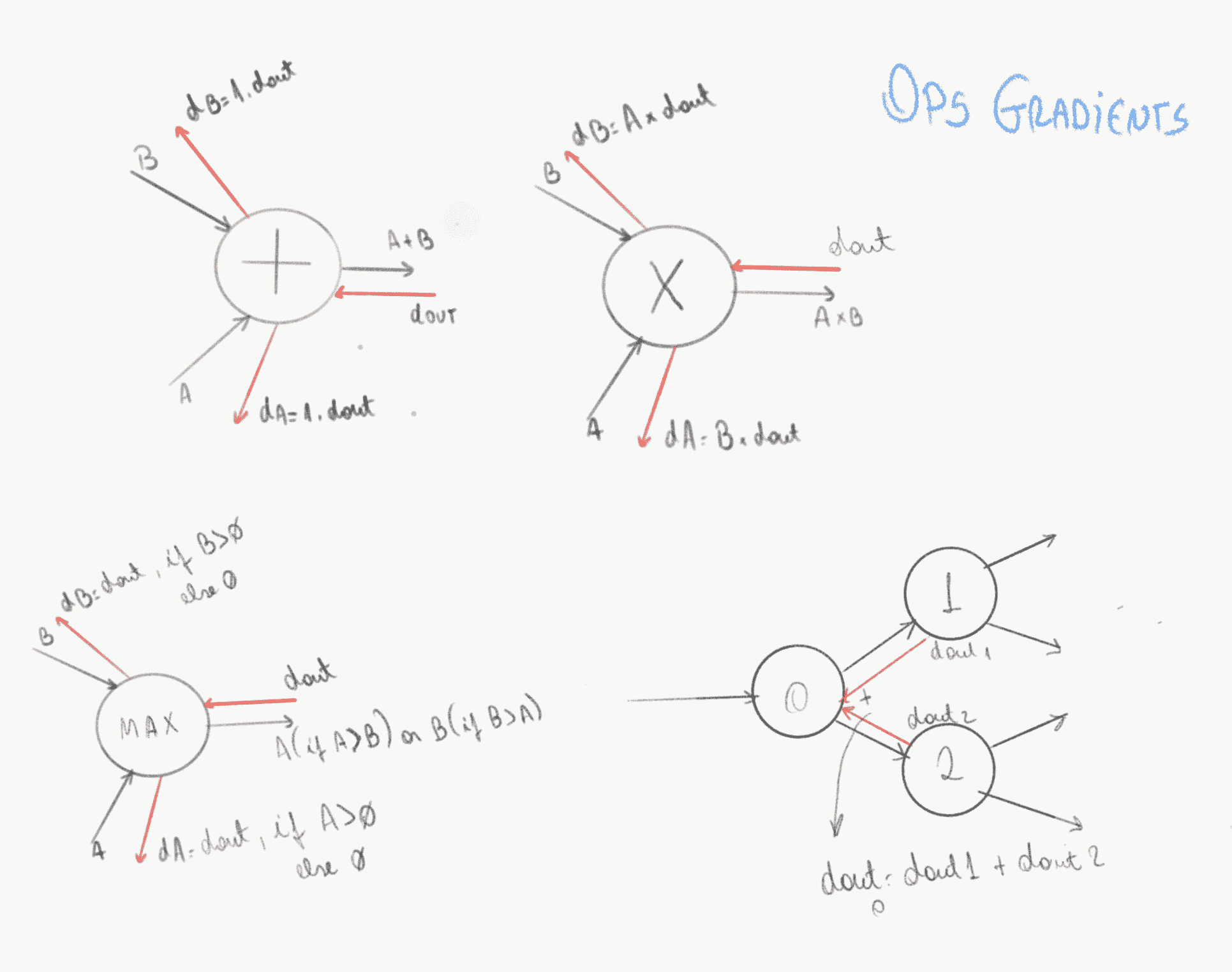   # 批量 對于大型數據集而言，將整個數據集存儲在內存中以訓練網絡的想法，例如第 1 章，“TensorFlow 簡介和設置”中的示例。 人們在實踐中所做的是，在訓練期間，他們將數據集分成小塊，稱為迷你批次（通常稱為批次）。 然后，依次將每個微型批次裝入并饋送到網絡，在網絡中將計算反向傳播和梯度下降算法，然后更新權重。 然后，對每個小批量重復此操作，直到您完全瀏覽了數據集。 為小批量計算的梯度是對整個訓練集的真實梯度的噪聲估計，但是通過反復獲取這些小的噪聲更新，我們最終仍將收斂到足夠接近損失函數的最小值。 較大的批次大小可以更好地估計真實梯度。 使用較大的批次大小將允許較大的學習率。 權衡是在訓練時需要更多的內存來保存此批次。 當模型看到您的整個數據集時，我們說一個周期已經完成。 由于訓練的隨機性，您將需要針對多個周期訓練模型，因為您的模型不可能只在一個周期內收斂。 # 損失函數 在訓練階段，我們需要使用當前的權重正確預測訓練集； 此過程包括評估我們的訓練集輸入 *X* ，并與所需的輸出 *Y* 進行比較。 需要某種機制來量化（返回標量數）我們當前的權重在正確預測我們所需的輸出方面有多好。 該機制稱為**損失函數**。 反向傳播算法應返回每個參數相對于損失函數的導數。 這意味著我們將發現更改每個參數將如何影響損失函數的值。 然后，優化算法的工作就是最小化損失函數，換句話說，就是在訓練時減小訓練誤差。 一個重要方面是為工作選擇合適的損失函數。 一些最常見的損失函數及其用途是在此處給出的： * **對數損失** - 僅具有兩個可能結果的分類任務（從有限集中返回標簽） * **交叉熵損失** - 具有兩個以上結果的分類任務（從有限集返回標簽） * **L1 損失** - 回歸任務（返回實數值） * **L2 損失** - 回歸任務（返回實數值） * **Huber 損失** - 回歸任務（返回實數值） 在本書中，我們將看到損失函數的不同示例。 損失函數的另一個重要方面是它們必須是可微分的。 否則，我們不能將它們與反向傳播一起使用。 這是因為反向傳播要求我們能夠采用損失函數的導數。 在下圖中，您可以看到損失函數連接在神經網絡的末端（模型輸出），并且基本上取決于模型的輸出和數據集所需的目標。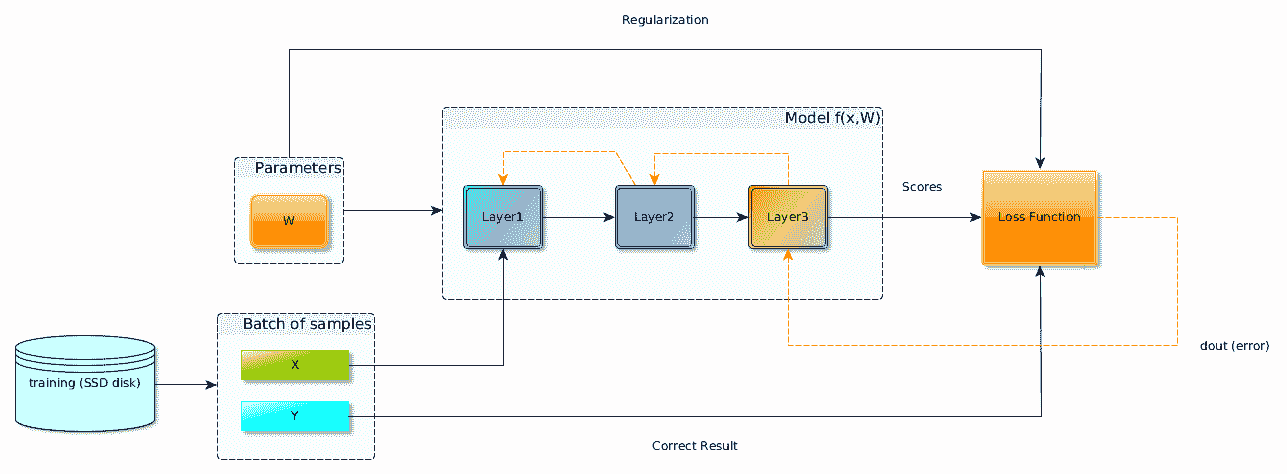  TensorFlow 的以下代碼行也顯示了這一點，因為損失僅需要標簽和輸出（此處稱為對率）。 ```py loss = tf.losses.sparse_softmax_cross_entropy(labels=labels, logits=logits) ``` 您可能會注意到第三個箭頭也連接到損失函數。 這與名為正則化的東西有關，將在第 3 章“TensorFlow 中的圖像分類”中進行探討； 因此，現在您可以放心地忽略它。 # 優化器及其超參數 如前所述，優化器的工作是以一種使訓練損失誤差最小的方式來更新網絡權重。 在所有 TensorFlow 之類的深度學習庫中，實際上只使用了一個優化器系列，即梯度下降式優化器系列。 其中最基本的簡稱為梯度下降（有時稱為香草梯度下降），但已經嘗試開發出更復雜的梯度下降方法。 一些受歡迎的是： * 帶動量的梯度下降 * RMSProp * Adam TensorFlow 的所有不同優化器都可以在`tf.train`類中找到。 例如，可以通過調用`tf.train.AdamOptimizer()`使用 Adam 優化器。 您可能會懷疑，它們都有可配置的參數來控制它們的工作方式，但是通常最需要注意和更改的參數如下： * 學習率：控制優化器嘗試最小化損失函數的速度。 將其設置得太高，您將無法收斂到最小。 將其設置得太小，將永遠收斂或陷于不良的局部最小值中。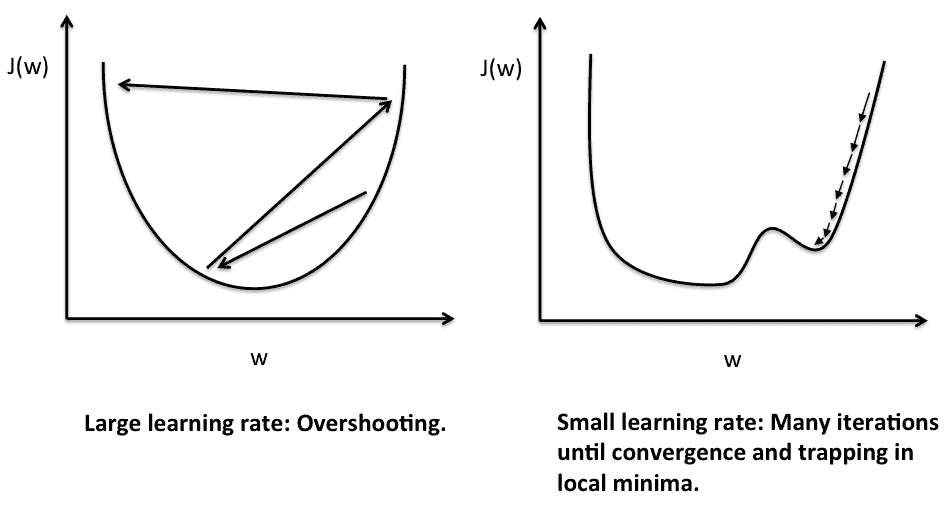 下圖顯示了學習率選擇錯誤可能帶來的問題：  學習率的另一個重要方面是，隨著訓練的進行和誤差的減少，您在訓練開始時選擇的學習率值可能會變得太大，因此您可能會開始超出最小值。 要解決此問題，您可以安排學習率衰減，以免在訓練時降低學習率。 這個過程稱為**學習率調度**，我們將在下一章中詳細討論幾種流行的方法。 另一種解決方案是使用自適應優化器之一，例如 Adam 或 RMSProp。 這些優化器經過精心設計，可在您訓練時自動調整和衰減所有模型參數的學習率。 這意味著從理論上講，您不必擔心安排自己的學習率下降。 最終，您希望選擇優化器，以最快，最準確的方式訓練您的網絡。 下圖顯示了優化器的選擇如何影響網絡收斂的速度。 不同的優化器之間可能會有相當大的差距，并且可能因不同的問題而有所不同，因此理想情況下，如果可以的話，您應該嘗試所有的優化器，并找到最適合您的問題的解決方案。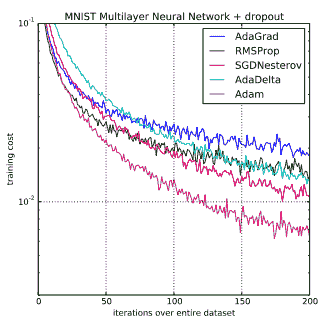  但是，如果您沒有時間執行此操作，那么下一個最佳方法是首先嘗試將 Adam 用作優化器，因為它通常在很少調整的情況下效果很好。 然后，如果有時間，請嘗試使用 Momentum SGD； 這將需要更多的參數調整，例如學習率，但是如果調整得很好，通常會產生非常好的結果。 # 欠擬合與過擬合 在設計用于解決特定問題的神經網絡時，我們可能有很多活動部件，并且必須同時處理許多事情，例如： * 準備數據集 * 選擇層數/神經元數 * 選擇優化器超參數 如果我們專注于第二點，它使我們了解選擇或設計神經網絡架構/結構時可能發生的兩個問題。 這些問題中的第一個是模型對于訓練數據的數量或復雜性而言是否太大。 由于模型具有如此眾多的參數，因此即使在數據中存在噪聲的情況下，它也可以輕松輕松地準確地學習其在訓練集中看到的內容。 這是一個問題，因為當向網絡提供的數據與訓練集不完全相同時，網絡將無法正常運行，因為它過于精確地了解了數據的外觀，而錯過了其背后的全局。 這個問題稱為**過擬合**或具有**高方差**。 另一方面，您可能選擇的網絡規模不足以捕獲數據復雜性。 現在，我們遇到了相反的問題，由于您的模型沒有足夠的能力（參數）來充分學習，因此您的模型無法充分捕獲數據集背后的基礎結構。 網絡將再次無法對新數據執行良好的操作。 這個問題稱為**欠擬合**或具有**高偏差**。 您可能會懷疑，在模型復雜性方面，您總是會尋求適當的平衡，以避免這些問題。 在后面的章節中，我們將看到如何檢測，避免和補救這些問題，但是僅出于介紹的目的，這些是解決這些問題的一些經典方法： * 獲取更多數據 * 當檢測到測試數據的誤差開始增長時停止（提前停止） * 盡可能簡單地開始模型設計，并且僅在檢測到欠擬合時才增加復雜性 # 特征縮放 為了簡化優化程序算法的工作，在訓練和測試之前，有一些技術可以并且應該應用到您的數據中。 如果輸入向量的不同維度上的值彼此不成比例，則損失空間將以某種方式擴大。 這將使梯度下降算法難以收斂，或者至少使其收斂較慢。 當數據集的特征超出比例時，通常會發生這種情況。 例如，關于房屋的數據集在輸入向量中的一個特征可能具有“房間數”，其值可能在 1 到 4 之間，而另一個特征可能是“房屋面積”，并且可能在 1000 到 10000 之間。 ，它們彼此之間嚴重超出比例，這可能會使學習變得困難。 在下面的圖片中，我們看到一個簡單的示例，說明如果我們的輸入特征未全部按比例縮放，則損失函數的外觀以及正確縮放比例后的外觀。 當數據縮放不正確時，梯度下降很難達到損失函數的最小值。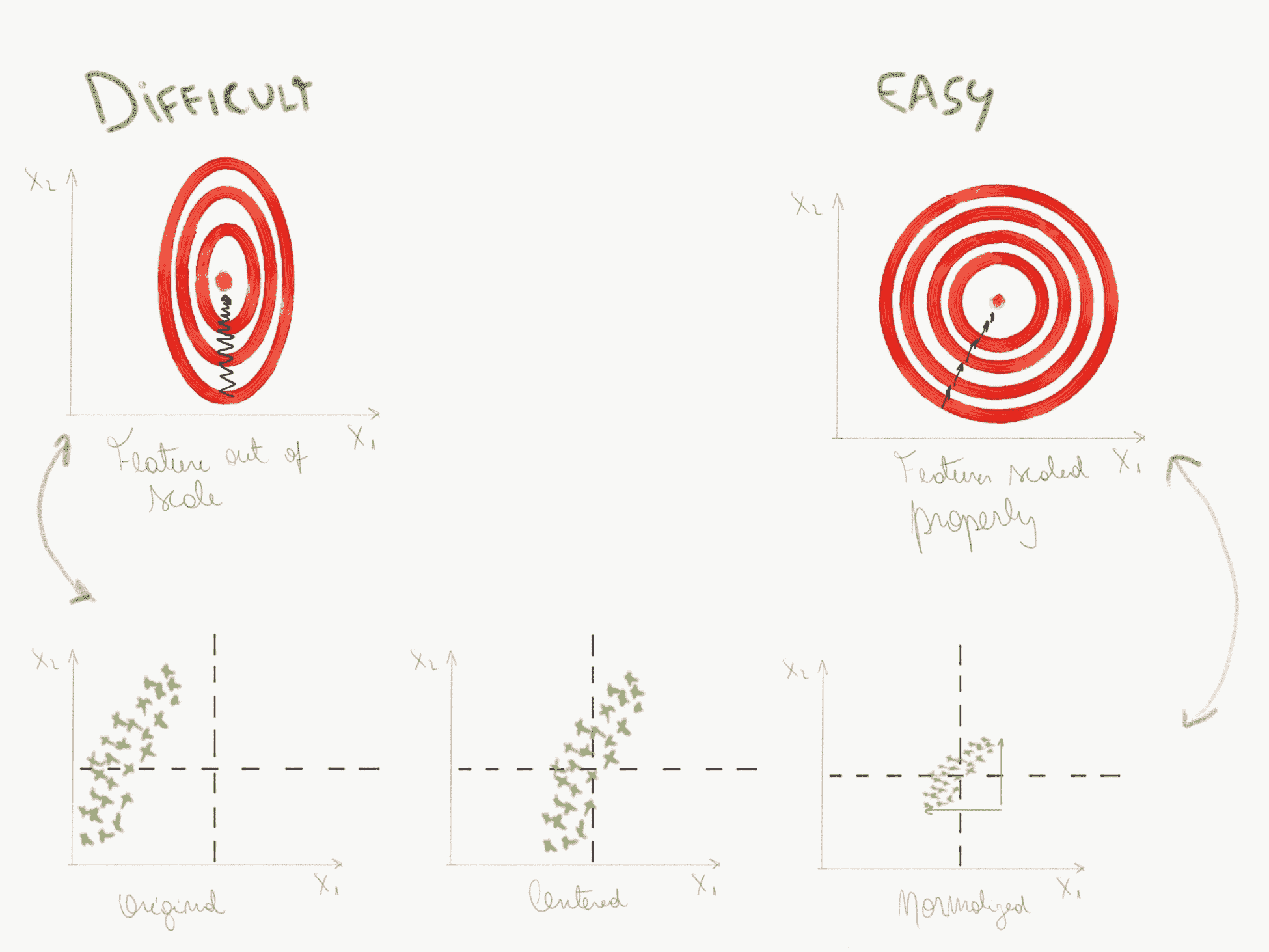  通常，您將對數據進行一些標準化，例如在使用數據之前減去平均值并除以數據集的標準差。 對于 RGB 圖像，通常只需從每個像素值中減去 128 即可使數據居中于零附近。 但是，更好的方法是為數據集中的每個圖像通道計算平均像素值。 現在，您具有三個值，每個圖像通道一個，現在從輸入圖像中刪除這些值。 我們一開始就不必擔心縮放問題，因為所有功能一開始的縮放比例都相同（0-255）。 要記住非常重要的一點-如果您在訓練時對數據進行了一些預處理，則必須在測試時進行完全相同的預處理，否則可能會得到不好的結果！ # 全連接層 組成我們之前看到的 ANN 的神經元層通常稱為密集連接層，或**全連接**（**FC**）層，或簡稱為線性層。 諸如 Caffe 之類的一些深度學習庫實際上會將它們視為點乘積運算，非線性層可能會或可能不會跟隨它們。 它的主要參數將是輸出大小，基本上是其輸出中神經元的數量。 在第 1 章，“TensorFlow 簡介和設置”中，我們創建了自己的致密層，但是您可以使用`tf.layers`來更輕松地創建它，如下所示： ```py dense_layer = tf.layers.dense(inputs=some_input_layer, units=1024, activation=tf.nn.relu) ``` 在這里，我們定義了一個具有 1,024 個輸出的完全連接層，隨后將激活 ReLU。 重要的是要注意，該層的輸入必須僅具有二維，因此，如果您的輸入是空間張量，例如形狀為`[28 * 28 * 3]`的圖像，則必須在輸入之前將其重整為向量： ```py reshaped_input_to_dense_layer = tf.reshape(spatial_tensor_in, [-1, 28 * 28 * 3]) ``` # 針對 XOR 問題的 TensorFlow 示例 在這里，我們將到目前為止已經了解的一些知識放在一起，并將使用 TensorFlow 解決布爾 XOR 問題。 在此示例中，我們將創建一個具有 Sigmoid 激活函數的三層神經網絡。 我們使用對數損失，因為網絡 0 或 1 僅有兩種可能的結果： ```py import tensorflow as tf # XOR dataset XOR_X = [[0, 0], [0, 1], [1, 0], [1, 1]] XOR_Y = [[0], [1], [1], [0]] num_input = 2 num_classes = 1 # Define model I/O (Placeholders are used to send/get information from graph) x_ = tf.placeholder("float", shape=[None, num_input], name='X') y_ = tf.placeholder("float", shape=[None, num_classes], name='Y') # Model structure H1 = tf.layers.dense(inputs=x_, units=4, activation=tf.nn.sigmoid) H2 = tf.layers.dense(inputs=H1, units=8, activation=tf.nn.sigmoid) H_OUT = tf.layers.dense(inputs=H2, units=num_classes, activation=tf.nn.sigmoid) # Define cost function with tf.name_scope("cost") as scope: cost = tf.losses.log_loss( labels=y_, predictions=H_OUT) # Add loss to tensorboard tf.summary.scalar("log_loss", cost) # Define training ops with tf.name_scope("train") as scope: train_step = tf.train.GradientDescentOptimizer(0.1).minimize(cost) merged_summary_op = tf.summary.merge_all() # Initialize variables(weights) and session init = tf.global_variables_initializer() sess = tf.Session() # Configure summary to output at given directory writer = tf.summary.FileWriter("./logs/xor_logs", sess.graph) sess.run(init) # Train loop for step in range(10000): # Run train_step and merge_summary_op _, summary = sess.run([train_step, merged_summary_op], feed_dict={x_: XOR_X, y_: XOR_Y}) if step % 1000 == 0: print("Step/Epoch: {}, Loss: {}".format(step, sess.run(cost, feed_dict={x_: XOR_X, y_: XOR_Y}))) # Write to tensorboard summary writer.add_summary(summary, step) ``` 如果運行此腳本，則應該期望獲得以下損失圖。 我們可以看到損失已經為零，這表明模型已經過訓練并解決了問題。 您可以重復此實驗，但現在只有一層致密層； 正如我們所說，您應該注意到該模型無法解決問題 。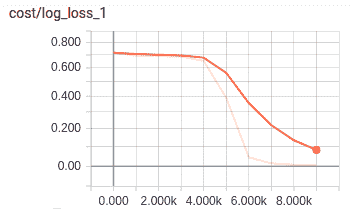 為了能夠查看圖，可以在腳本提示符下的命令提示符下運行以下命令。 這將為我們啟動 tensorboard。 我們將在本章的后面找到關于 tensorboard 的更多信息。 ```py $ tensorboard --logdir=./logs/xor_logs ``` # 卷積神經網絡 現在，我們將討論另一種類型的神經網絡，該網絡專門設計用于處理具有某些空間特性的數據，例如圖像。 這種類型的神經網絡稱為**卷積神經網絡**（**CNN**）。 CNN 主要由稱為**卷積層**的層組成，這些層對其層輸入進行過濾以在這些輸入中找到有用的特征。 這種過濾操作稱為卷積，從而產生了這種神經網絡的名稱。 下圖顯示了對圖像的二維卷積運算及其結果。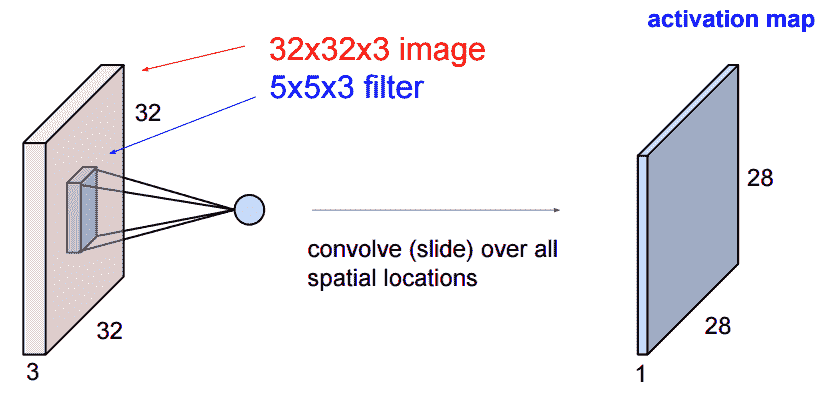 重要的是要記住，過濾器內核的深度與輸入的深度相匹配（在這種情況下為 3）：  同樣重要的是要清楚卷積層的輸入不必是 1 或 3 通道圖像。 卷積層的輸入張量可以具有任意數量的通道。 很多時候，在談論 CNN 中的卷積層時，人們都喜歡將卷積這個詞簡稱為`conv`。 這是非常普遍的做法，我們在本書中也會做同樣的事情。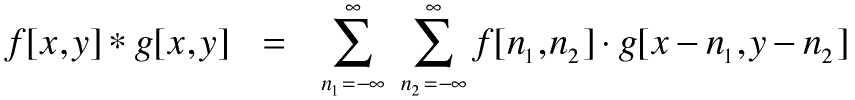 # 卷積 卷積運算是由星號表示的線性運算，它將兩個信號合并：  二維卷積在圖像處理中用于實現圖像過濾器，例如，查找圖像上的特定補丁或查找圖像中的某些特征。 在 CNN 中，卷積層使用稱為**內核**的小窗口，以類似于瓦片的方式過濾輸入張量。 內核精確定義了卷積運算將要過濾的內容，并且在找到所需內容時會產生強烈的響應。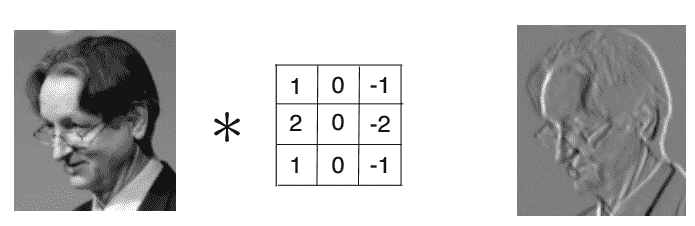 下圖顯示了將圖像與稱為 Sobel 過濾器的特定內核進行卷積的結果，該內核非常適合在圖像中查找邊：  您可能已經猜到了，在卷積層中要學習的參數是該層內核的權重。 在 CNN 訓練期間，這些過濾器的值會自動調整，以便為手頭任務提取最有用的信息。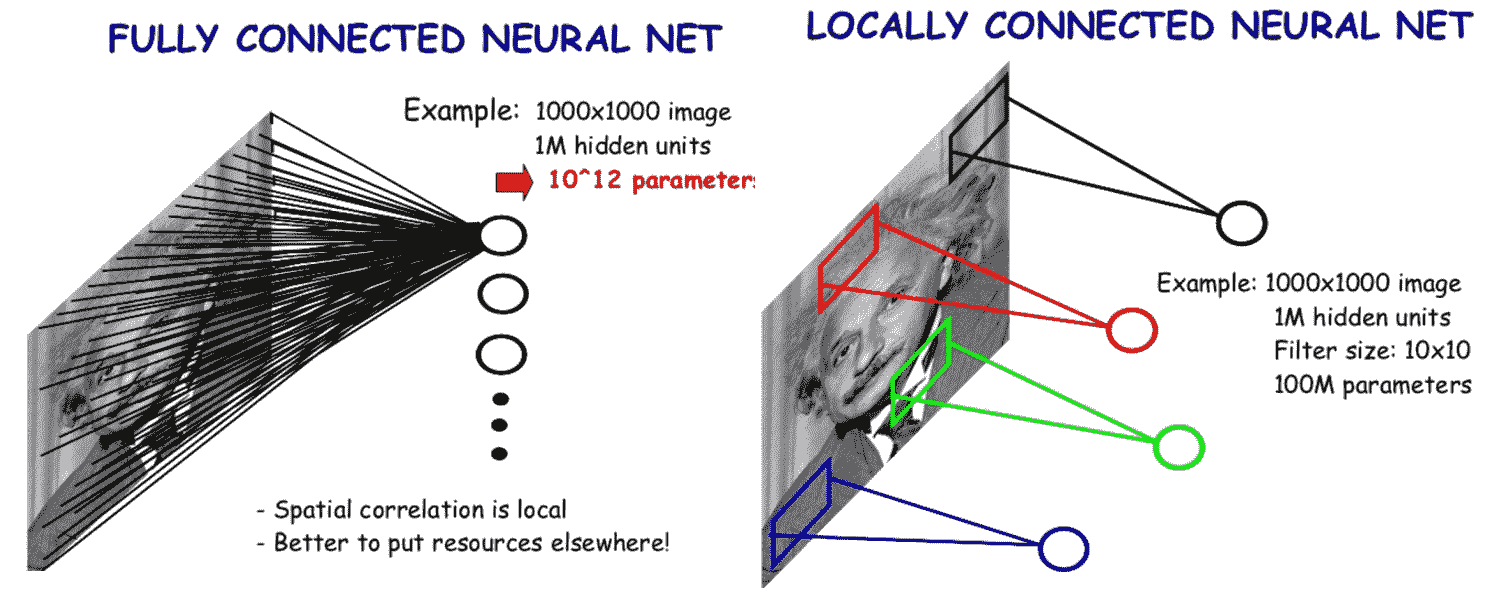 在傳統的神經網絡中，我們將必須將任何輸入數據轉換為單個一維向量，從而在將該向量發送到全連接層后丟失所有重要的空間信息。 此外，每個像素每個神經元都有一個參數，導致輸入大小或輸入深度較大的模型中參數數量激增。 但是，在卷積層的情況下，每個內核將在整個輸入中“滑動”以搜索特定補丁。 CNN 中的內核很小，并且與它們所卷積的大小無關。 結果，就參數而言，使用卷積層的開銷通常比我們之前了解的傳統密集層要少得多。 下圖顯示了傳統的完全連接層和卷積（局部連接）層之間的區別。 注意參數的巨大差異：  現在，也許我們希望卷積層在其輸入中查找六種不同的事物，而不僅僅是尋找一種。 在這種情況下，我們將只給卷積層六個相同大小的過濾器（在這種情況下為`5x5x3`），而不是一個。 然后，每個轉換過濾器都會在輸入中查找特定的模式。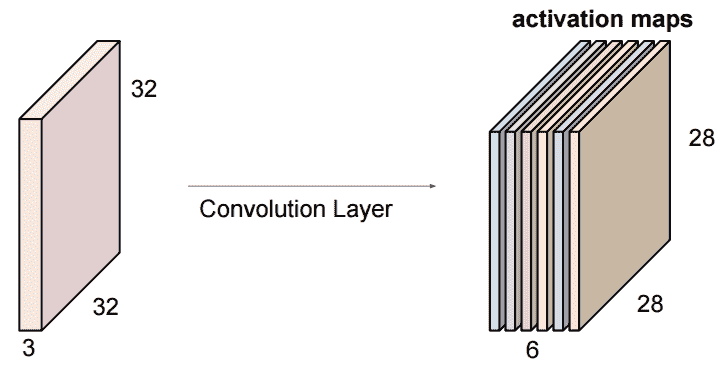 下圖顯示了此特定的六個過濾器卷積層的輸入和輸出：  控制卷積層行為的主要超參數如下： * **內核大小（K）**：滑動窗口的像素大小。 小通常更好，通常使用奇數，例如 1、3、5，有時很少使用 7。 * **跨度（S）**：內核窗口在卷積的每個步驟中將滑動多少像素。 通常將其設置為 1，因此圖像中不會丟失任何位置，但是如果我們想同時減小輸入大小，則可以增加位置。 * **零填充（P）**：要放在圖像邊框上的零數量。 使用填充使內核可以完全過濾輸入圖像的每個位置，包括邊。 * **過濾器數（F）**：我們的卷積層將具有多少個過濾器。 它控制卷積層將要查找的圖案或特征的數量。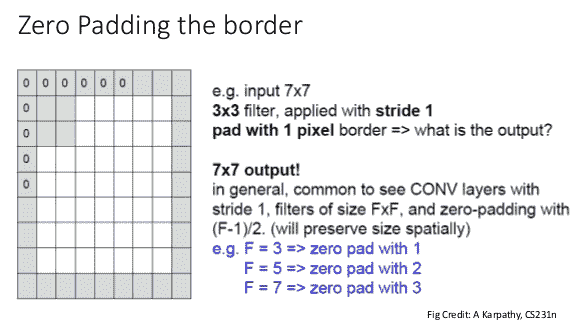 在 TensorFlow 中，我們將在`tf.layers`模塊中找到 2D 卷積層，可以將其添加到模型中，如下所示： ```py conv1 = tf.layers.conv2d( inputs=input_layer, filters=32, kernel_size=[5, 5], padding="same", activation=tf.nn.relu) ``` # 輸入填充 如果我們什么都不做，那么卷積運算將輸出一個在空間上小于輸入結果的結果。 為了避免這種影響并確保卷積核查看每個圖像位置，我們可以在輸入圖像的邊界上放置零。 當我們這樣做時，據說我們要填充圖像：  TensorFlow 卷積操作為您提供了兩種用于填充需求的選項：相同和有效。 * 有效-TensorFlow 不填充圖像。 卷積內核將僅進入輸入中的“有效”位置。 * 相同-如果我們假設步幅為 1，則在這種情況下，TensorFlow 將足夠填充輸入，以便輸出空間大小與輸入空間大小相同。 如果您確實希望對填充有更多控制，則可以在層的輸入上使用`tf.pad()`，以用所需的零個位數來填充輸入。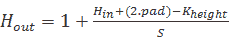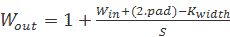 通常，我們可以使用以下公式計算卷積運算的輸出大小：   （這里，`pad`是添加到每個邊框的零的數量。） 但是在 TensorFlow 中，由于有效和相同填充選項的性質，公式如下所示： ```py # Same padding out_height = ceil(float(in_height) / float(strides[1])) out_width = ceil(float(in_width) / float(strides[2])) # Valid padding out_height = ceil(float(in_height - filter_height + 1) / float(strides[1])) out_width = ceil(float(in_width - filter_width + 1) / float(strides[2])) ``` # 計算參數數量（權重） 在這里，我們將展示如何計算卷積層使用的參數數量。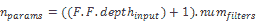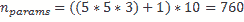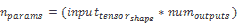 計算卷積層中參數數量（包括偏差）的公式如下：  我們將用一個簡單的例子來說明： ```py Input: [32x32x3] input tensor Conv layer: Kernel:5x5 numFilters:10 ```  另一方面，全連接層中的參數數量（包括偏置）如下：  如前所述，如果直接在圖像上使用傳統的人工神經網絡，則所有空間信息都將丟失，并且每個參數每個神經元每個像素只有一個參數，因此會有大量的參數。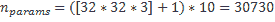 使用前面提到的相同示例，并在密集的 10 個輸出神經元層中，我們得到以下數字：  這證明了這兩種層類型之間參數的數量級差異。 # 計算操作數量 現在，我們對計算特定卷積層的計算成本感興趣。 如果您想了解如何實現有效的網絡結構（例如在移動設備中速度是關鍵時），則此步驟很重要。 另一個原因是要查看在硬件中實現特定層需要多少個乘法器。 現代 CNN 架構中的卷積層最多可負責模型中所有計算的 90%！ 這些是影響 MAC（乘加累加器）/操作數量的因素： * 卷積核大小（`F`） * 過濾器數量（`M`） * 輸入特征圖的高度和寬度（`H`，`W`） * 輸入批量（`B`） * 輸入深度大小（通道）（`C`） * 卷積層步幅（`S`） MAC 的數量可以計算為： ```py #MAC = [F * F * C * (H + 2 * P-FS + 1) * (W + 2 * P-FS + 1) * M] * B ``` 例如，讓我們考慮一個具有輸入`224 x 224 x 3`，批量大小為 1，內核為`3x3`、64 個過濾器，跨度為 1 和填充 1 的轉換層： ```py #MAC = 3 * 3 * (224 + 2-31 + 1) * (224 + 2-31 + 1) * 3 * 64 * 1 = 9,462,528 ``` 相反，全連接層具有以下操作數： ```py #MAC = [H * W * C * Outputneurons] * B ``` 讓我們重用相同的示例，但現在有 64 個神經元的密集層： ```py #MAC = [224 * 224 * 3 * 64] * 1 = 9,633,792 ``` （我們已排除了所有運維計算的偏差，但不應增加太多成本。） 通常，在 CNN 中，早期的卷積層貢獻了大部分計算成本，但參數最少。 在網絡的末尾，相反的情況是后面的層具有更多的參數，但計算成本卻較低。 # 將卷積層轉換為全連接層 實際上，我們可以將全連接層視為卷積層的子集。 如果我們將內核大小設置為與輸入大小匹配，則可以將 CNN 層轉換為全連接層。 設置過濾器的數量與設置完全連接層中輸出神經元的數量相同。 檢查一下自己，在這種情況下，操作將是相同的。 例： 考慮具有 4,096 個輸出神經元和輸入大小為`7x7x512`的 FC 層，轉換為： 轉換層：內核：`7x7`，填充：0：步幅：1，過濾器：4,096。 使用公式來計算輸出大小，我們得到大小為`1 x 1 x 4096`的輸出。 這樣做的主要原因之一是使您的網絡完全卷積。 當網絡完全卷積時，決定使用比輸入的圖像更大的輸入大小圖像并不重要，因為您沒有任何需要固定輸入大小的全連接層。 # 池化層 **池化層**用于減少 CNN 中我們的激活張量的空間尺寸，而不是體積深度。 它們是執行此操作的非參數方式，這意味著池化層中沒有權重。 基本上，以下是從使用池中獲得的收益： * 在輸入張量中匯總空間相關信息的簡單方法 * 通過減少空間信息，您可以獲得計算性能 * 您的網絡中存在一些平移不變性 但是，池化的最大優點之一是它無需學習任何參數，這也是它的最大缺點，因為池化最終可能會丟掉重要的信息。 結果，現在開始在 CNN 中使用池的頻率降低了。 在此圖中，我們顯示了最大池化池的最常見類型。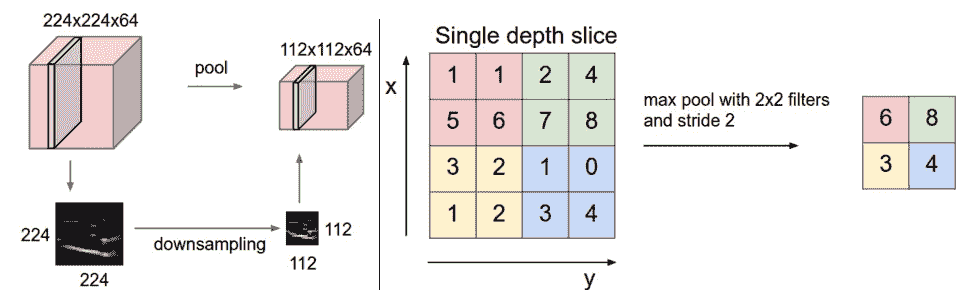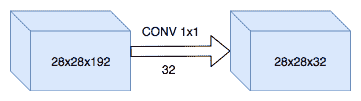 它像普通的卷積一樣滑動一個窗口，然后在每個位置將窗口中的最大值設置為輸出：  在 TensorFlow 中，我們可以這樣定義池層： ```py tf.layers.max_pooling2d(inputs=some_input_layer, pool_size=[2, 2], strides=2) ``` # `1x1`卷積 這種卷積起初看起來可能有些奇怪，但是`1x1`卷積實際上是通過合并深度來適應深度的，而不更改空間信息。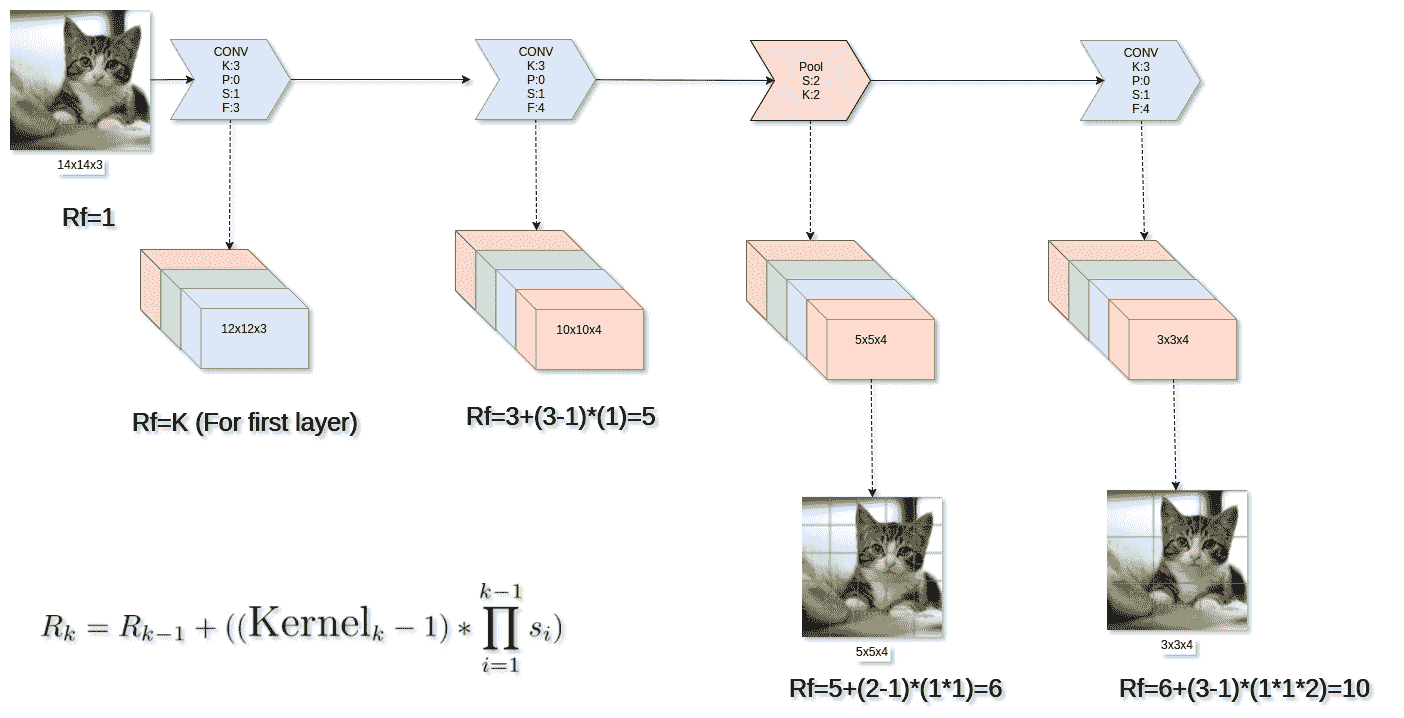 當需要在不損失空間信息的情況下將一個體積深度轉換為另一個體積深度（稱為壓縮或擴展）時，可以使用這種類型的卷積：  # 計算感受域 感受域是特定卷積窗口“看到”其輸入張量的程度。 有時，確切了解激活中每個特定像素在輸入圖像中“看到”了多少像素可能很有用； 這在對象檢測系統中尤其重要，因為我們需要以某種方式查看某些層激活如何映射回原始圖像大小。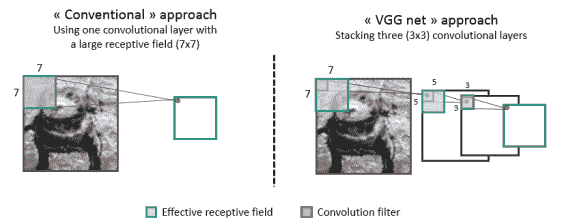 在下圖中，我們可以看到三個連續的`3x3`卷積層的感受域與一個`7x7`卷積層的感受域相同。 在設計新的更好的 CNN 模型時，此屬性非常重要，我們將在后面的章節中看到。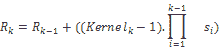  感受域可以計算為：  在這里，組件如下： * `R[k]`：`k`層的感受域 * `Kernel[k]`：第`k`層的內核大小 * `S[i]`：第`i`層（`1..k-1`）的跨步 * `∏s[i], i=1..(k-1)`：直到第`k-1`層的所有步長的乘積（所有先前的層，而不是當前的一層） 僅對于第一層，接收域就是內核大小。 這些計算與是否使用卷積或池化層無關，例如，步幅為 2 的卷積層將與步幅為 2 的池化層具有相同的感受域。 例如，給定以下層之后的`14x14x3`圖像，這將適用： * 卷積：S：1，P：0，K：3 * 卷積：S：1，P：0，K：3 * 最大池化：S：2，P：0，K2 * 卷積：S：1，P：0，K：3  # 在 TensorFlow 中構建 CNN 模型 在開始之前，有個好消息：使用 TensorFlow，您無需擔心編寫反向傳播或梯度下降代碼，而且所有常見類型的層都已實現，因此事情應該更輕松。 在此處的 TensorFlow 示例中，我們將根據您在第 1 章，“TensorFlow 簡介和設置”中學到的內容進行一些更改，并輕松自如地使用`tf.layers` API 創建我們的整個網絡： ```py import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data mnist = input_data.read_data_sets("MNIST_data/", one_hot=True) # MNIST data input (img shape: 28*28) num_input = 28*28*1 # MNIST total classes (0-9 digits) num_classes = 10 # Define model I/O (Placeholders are used to send/get information from graph) x_ = tf.placeholder("float", shape=[None, num_input], name='X') y_ = tf.placeholder("float", shape=[None, num_classes], name='Y') # Add dropout to the fully connected layer is_training = tf.placeholder(tf.bool) # Convert the feature vector to a (-1)x28x28x1 image # The -1 has the same effect as the "None" value, and will # be used to inform a variable batch size x_image = tf.reshape(x_, [-1, 28, 28, 1]) # Convolutional Layer #1 # Computes 32 features using a 5x5 filter with ReLU activation. # Padding is added to preserve width and height. # Input Tensor Shape: [batch_size, 28, 28, 1] # Output Tensor Shape: [batch_size, 28, 28, 32] conv1 = tf.layers.conv2d(inputs=x_image, filters=32, kernel_size=[5, 5], padding="same", activation=tf.nn.relu) # Pooling Layer #1 # First max pooling layer with a 2x2 filter and stride of 2 # Input Tensor Shape: [batch_size, 28, 28, 32] # Output Tensor Shape: [batch_size, 14, 14, 32] pool1 = tf.layers.max_pooling2d(inputs=conv1, pool_size=[2, 2], strides=2) # Convolutional Layer #2 # Computes 64 features using a 5x5 filter. # Input Tensor Shape: [batch_size, 14, 14, 32] # Output Tensor Shape: [batch_size, 14, 14, 64] conv2 = tf.layers.conv2d( inputs=pool1, filters=64, kernel_size=[5, 5], padding="same", activation=tf.nn.relu) # Pooling Layer #2 # Second max pooling layer with a 2x2 filter and stride of 2 # Input Tensor Shape: [batch_size, 14, 14, 64] # Output Tensor Shape: [batch_size, 7, 7, 64] pool2 = tf.layers.max_pooling2d(inputs=conv2, pool_size=[2, 2], strides=2) # Flatten tensor into a batch of vectors # Input Tensor Shape: [batch_size, 7, 7, 64] # Output Tensor Shape: [batch_size, 7 * 7 * 64] pool2_flat = tf.reshape(pool2, [-1, 7 * 7 * 64]) # Dense Layer # Densely connected layer with 1024 neurons # Input Tensor Shape: [batch_size, 7 * 7 * 64] # Output Tensor Shape: [batch_size, 1024] dense = tf.layers.dense(inputs=pool2_flat, units=1024, activation=tf.nn.relu) # Add dropout operation; 0.6 probability that element will be kept dropout = tf.layers.dropout( inputs=dense, rate=0.4, training=is_training) # Logits layer # Input Tensor Shape: [batch_size, 1024] # Output Tensor Shape: [batch_size, 10] logits = tf.layers.dense(inputs=dropout, units=10) # Define a loss function (Multinomial cross-entropy) and how to optimize it cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=y_)) train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy) correct_prediction = tf.equal(tf.argmax(logits,1), tf.argmax(y_,1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) # Build graph init = tf.global_variables_initializer() # Avoid allocating the whole memory gpu_options = tf.GPUOptions(per_process_gpu_memory_fraction=0.333) sess = tf.Session(config=tf.ConfigProto(gpu_options=gpu_options)) sess.run(init) # Train graph for i in range(2000): # Get batch of 50 images batch = mnist.train.next_batch(50) # Print each 100 epochs if i % 100 == 0: # Calculate train accuracy train_accuracy = accuracy.eval(session=sess, feed_dict={x_: batch[0], y_: batch[1], is_training: True}) print("step %d, training accuracy %g" % (i, train_accuracy)) # Train actually here train_step.run(session=sess, feed_dict={x_: batch[0], y_: batch[1], is_training: False}) print("Test Accuracy:",sess.run(accuracy, feed_dict={x_: mnist.test.images, y_: mnist.test.labels, is_training: False})) ``` # TensorBoard TensorBoard 是 TensorFlow 隨附的基于 Web 的工具，可讓您可視化構造的 TensorFlow 圖。 最重要的是，它使您能夠跟蹤大量的統計數據或變量，這些數據或變量可能對訓練模型很重要。 您可能希望跟蹤的此類變量的示例包括訓練損失，測試集準確率或學習率。 前面我們看到，我們可以使用張量板可視化損失函數的值。 要運行 TensorBoard，請打開一個新終端并輸入以下內容： ```py $ tensorboard --logdir=/somepath ``` 在這里，`somepath`指向您的訓練代碼保存張量板日志記錄數據的位置。 在代碼內部，您需要通過為每個張量創建一個`tf.summary`來定義要可視化的張量。 因此，例如，如果我們要檢查所有可訓練變量和損失，則需要使用以下代碼： ```py with tf.Session() as sess: """Create your model""" # Add all trainable variables to tensorboard for var in tf.trainable_variables(): tf.summary.histogram(var.name, var) # Add loss to tensorboard tf.summary.scalar("softmax_cross_entropy", loss) # Merge all summaries merged_summary = tf.summary.merge_all() # Initialize a summary writer train_writer = tf.summary.FileWriter( /tmp/summarys/ , sess.graph) train_writer.add_summary(merged_summary, global_step) """Training loop""" ``` 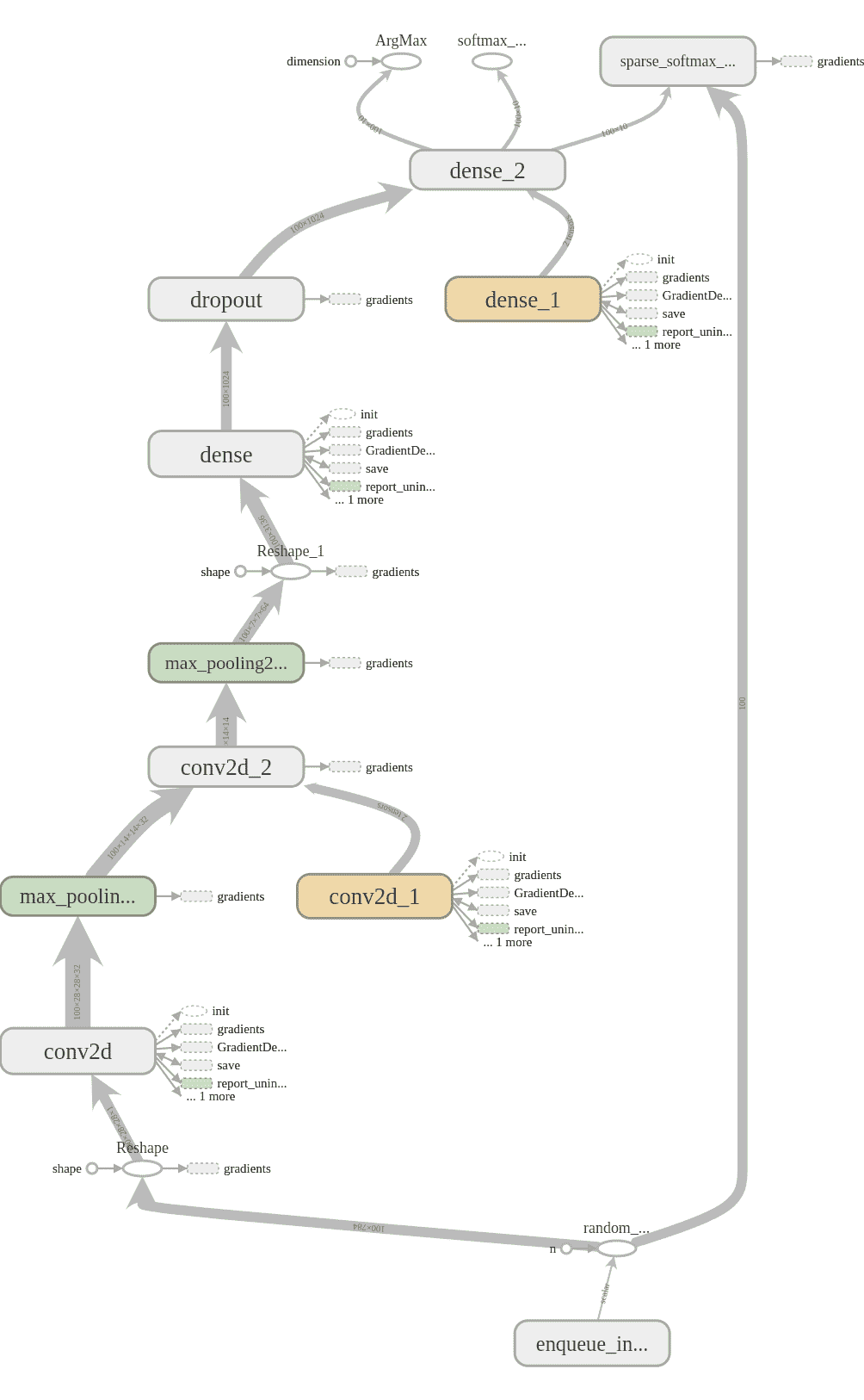我們需要創建一個`tf.summar.FileWriter`，它負責創建一個目錄，該目錄將存儲我們的摘要日志。 如果在創建`FileWriter`時傳遞圖，則該圖也將顯示在 TensorBoard 中。 通過傳入`sess.graph`，我們提供了會話正在使用的默認圖。 在 TensorBoard 中顯示圖的結果可能看起來像這樣：  # 其他類型的卷積 本章的目的是讓您了解 CNN 是什么，它們的用途以及如何在 TensorFlow 中構造它們。 但是，在這一點上值得一提的是，當今還有其他類型的卷積運算用于不同的目的，我們將在后面的章節中更詳細地介紹其中的一些。 現在，我們將僅按名稱和使用位置提及它們： * **深度卷積**：用于 MobileNets，旨在使卷積對移動平臺友好 * **膨脹卷積（Atrous Convolution）**：它們具有稱為膨脹率的額外參數，可讓您以相同的計算成本獲得更大的視野（例如`3x3`卷積可以和`5x5`卷積具有相同的視野） * **轉置卷積（Deconvolutions）**：通常用于 CNN 自編碼器和語義分割問題 # 總結 在本章中，我們向您介紹了機器學習和人工智能。 我們研究了什么是人工神經網絡以及如何對其進行訓練。 在此之后，我們研究了 CNN 及其主要組成部分。 我們介紹了如何使用 TensorFlow 訓練您自己的 CNN 以識別數字。 最后，我們對 Tensorboard 進行了介紹，并了解了如何在 TensorFlow 中訓練模型時如何使用它來幫助可視化重要的統計數據。 在下一章中，我們將更仔細地研究圖像分類的任務，以及如何使用 CNN 和 TensorFlow 來解決此任務。