# 二、TensorFlow v1.6 的新功能是什么？ 2015 年，Google 開源了 TensorFlow，包括其所有參考實現。所有源代碼都是在 Apache 2.0 許可下在 GitHub 上提供的。從那以后，TensorFlow 已經在學術界和工業研究中被廣泛采用，最穩定的版本 1.6 最近已經發布了統一的 API。 值得注意的是，TensorFlow 1.6（及更高版本）中的 API 并非都與 v1.5 之前的代碼完全向后兼容。這意味著一些在 v1.5 之前工作的程序不一定適用于 TensorFlow 1.6。 現在讓我們看看 TensorFlow v1.6 具有的新功能和令人興奮的功能。 ## Nvidia GPU 支持的優化 從 TensorFlow v1.5 開始，預構建的二進制文件現在針對 CUDA 9.0 和 cuDNN 7 構建。但是，從 v1.6 版本開始，TensorFlow 預構建的二進制文件使用 AVX 指令，這可能會破壞舊 CPU 上的 TensorFlow。盡管如此，自 v1.5 以來，已經可以在 NVIDIA Tegra 設備上增加對 CUDA 的支持。 ## TensorFlow Lite TensorFlow Lite 是 TensorFlow 針對移動和嵌入式設備的輕量級解決方案。它支持具有小二進制大小和支持硬件加速的快速表現的設備上機器學習模型的低延遲推理。 TensorFlow Lite 使用許多技術來實現低延遲，例如優化特定移動應用的內核，預融合激活，允許更小和更快（定點數學）模型的量化內核，以及將來利用杠桿專用機器學習硬件在特定設備上獲得特定模型的最佳表現。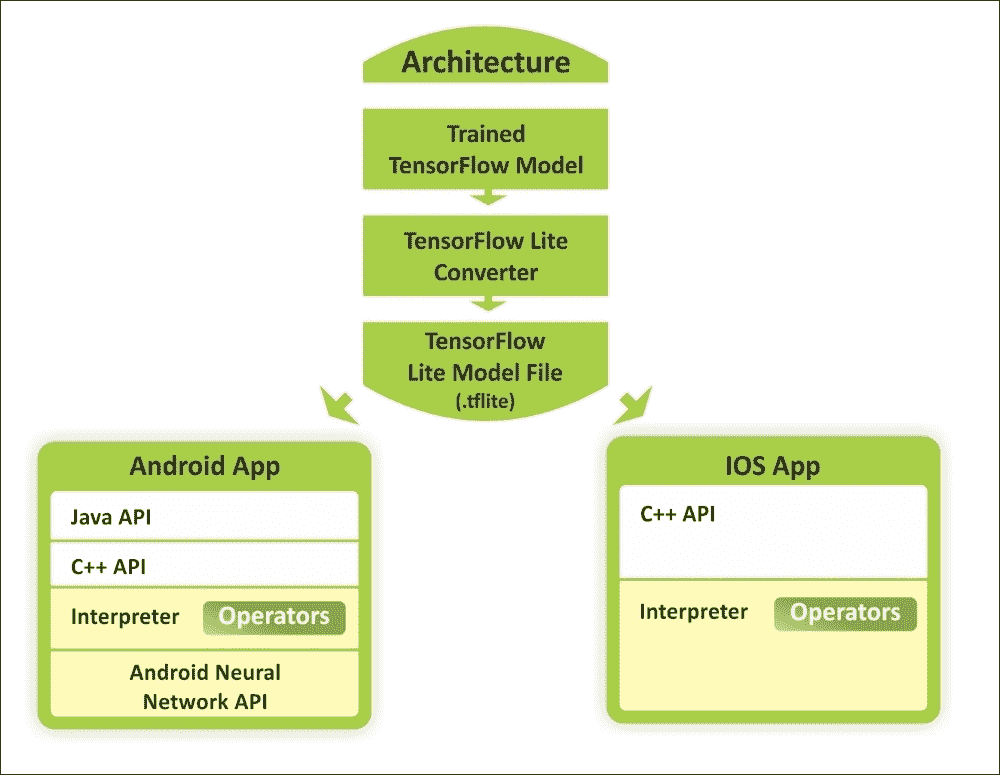  圖 1：使用 TensorFlow Lite 在 Android 和 iOS 設備上使用訓練模型的概念視圖 機器學習正在改變計算范式，我們看到了移動和嵌入式設備上新用例的新趨勢。在相機和語音交互模型的推動下，消費者的期望也趨向于與其設備進行自然的，類似人的交互。 因此，用戶的期望不再局限于計算機，并且移動設備的計算能力也因硬件加速以及諸如 Android 神經??網絡 API 和 iOS 的 C++ API 之類的框架而呈指數級增長。如上圖所示，預訓練模型可以轉換為較輕的版本，以便作為 Android 或 iOS 應用運行。 因此，廣泛使用的智能設備為設備智能創造了新的可能性。這些允許我們使用我們的智能手機來執行實時計算機視覺和自然語言處理（NLP）。 ## 急切執行 急切執行是 TensorFlow 的一個接口，它提供了一種命令式編程風格。啟用預先執行時，TensorFlow 操作（在程序中定義）立即執行。 需要注意的是，從 TensorFlow v1.7 開始，急切執行將被移出`contrib`。這意味著建議使用`tf.enable_eager_execution()`。我們將在后面的部分中看到一個例子。 ## 優化加速線性代數（XLA） v1.5 之前的 XLA 不穩定并且具有非常有限的特性。但是，v1.6 對 XLA 的支持更多。這包括以下內容： * 添加了對 XLA 編譯器的 Complex64 支持 * 現在為 CPU 和 GPU 添加了快速傅里葉變換（FFT）支持 * `bfloat`支持現已添加到 XLA 基礎結構中 * 已啟用 ClusterSpec 傳播與 XLA 設備的工作 * Android TF 現在可以在兼容的 Tegra 設備上使用 CUDA 加速構建 * 已啟用對添加確定性執行器以生成 XLA 圖的支持 開源社區報告的大量錯誤已得到修復，并且此版本已集成了大量 API 級別的更改。 但是，由于我們尚未使用 TensorFlow 進行任何研究，我們將在后面看到如何利用這些功能開發真實的深度學習應用。在此之前，讓我們看看如何準備您的編程環境。 # 安裝和配置 TensorFlow 您可以在許多平臺上安裝和使用 TensorFlow，例如 Linux， macOS 和 Windows。此外，您還可以從 TensorFlow 的最新 GitHub 源構建和安裝 TensorFlow。此外，如果您有 Windows 機器，您可以通過原生點或 Anacondas 安裝 TensorFlow。 TensorFlow 在 Windows 上支持 Python 3.5.x 和 3.6.x. 此外，Python 3 附帶了 PIP3 包管理器，它是用于安裝 TensorFlow 的程序。因此，如果您使用此 Python 版本，則無需安裝 PIP。根據我們的經驗，即使您的計算機上集成了 NVIDIA GPU 硬件，也值得安裝并首先嘗試僅使用 CPU 的版本，如果您沒有獲得良好的表現，那么您應該切換到 GPU 支持。 支持 GPU 的 TensorFlow 版本有幾個要求，例如 64 位 Linux，Python 2.7（或 Python 3 的 3.3+），NVIDIACUDA?7.5 或更高版本（Pascal GPU 需要 CUDA 8.0）和 NVIDIA cuDNN（這是 GPU 加速深度學習）v5.1（建議使用更高版本）。有關詳情，請參閱[此鏈接](https://developer.nvidia.com/cudnn)。 更具體地說，TensorFlow 的當前開發僅支持使用 NVIDIA 工具包和軟件的 GPU 計算。因此，必須在您的計算機上安裝以下軟件才能獲得預測分析應用的 GPU 支持： * NVIDIA 驅動程序 * 具有計算能力的`CUDA >= 3.0` * CudNN NVIDIA CUDA 工具包包括（詳見[此鏈接](https://developer.nvidia.com/cuda-zone)）： * GPU 加速庫，例如用于 FFT 的 cuFFT * 基本線性代數子程序（BLAS）的 cuBLAS * cuSPARSE 用于稀疏矩陣例程 * cuSOLVER 用于密集和稀疏的直接求解器 * 隨機數生成的 cuRAND，圖像的 NPP 和視頻處理原語 * 適用于 NVIDIA Graph Analytics 庫的 nvGRAPH * 對模板化并行算法和數據結構以及專用 CUDA 數學庫的推動 但是，我們不會介紹 TensorFlow 的安裝和配置，因為 TensorFlow 上提供的文檔非常豐富，可以遵循并采取相應的措施。另一個原因是該版本將定期更改。因此，[使用 TensorFlow 網站](https://www.tensorflow.org/install/)保持自己更新將是一個更好的主意。 如果您已經安裝并配置了編程環境，那么讓我們深入了解 TensorFlow 計算圖。 # TensorFlow 計算圖 在考慮執行 TensorFlow 程序時，我們應該熟悉圖創建和會話執行的概念。基本上，第一個用于構建模型，第二個用于提供數據并獲得結果。 有趣的是，TensorFlow 在 C++ 引擎上執行所有操作，這意味著在 Python 中甚至不會執行一些乘法或添加操作。 Python 只是一個包裝器。從根本上說，TensorFlow C++ 引擎包含以下兩件事： * 有效的操作實現，例如 CNN 的卷積，最大池化和 sigmoid * 前饋模式操作的衍生物 TensorFlow 庫在編碼方面是一個非凡的庫，它不像傳統的 Python 代碼（例如，你可以編寫語句并執行它們）。 TensorFlow 代碼由不同的操作組成。甚至變量初始化在 TensorFlow 中也很特殊。當您使用 TensorFlow 執行復雜操作（例如訓練線性回歸）時，TensorFlow 會在內部使用數據流圖表示其計算。該圖稱為計算圖，它是由以下組成的有向圖： * 一組節點，每個節點代表一個操作 * 一組有向弧，每個弧代表執行操作的數據 TensorFlow 有兩種類型的邊： * 正常：它們攜帶節點之間的數據結構。一個操作的輸出，即來自一個節點的輸出，成為另一個操作的輸入。連接兩個節點的邊緣帶有值。 * 特殊：此邊不攜帶值，但僅表示兩個節點之間的控制依賴關系，例如 X 和 Y。這意味著只有在 X 中的操作已經執行時才會執行節點 Y，但之前關于數據的操作之間的關系。 TensorFlow 實現定義控制依賴性，以強制規定執行其他獨立操作的順序，作為控制峰值內存使用的方式。 計算圖基本上類似于數據流圖。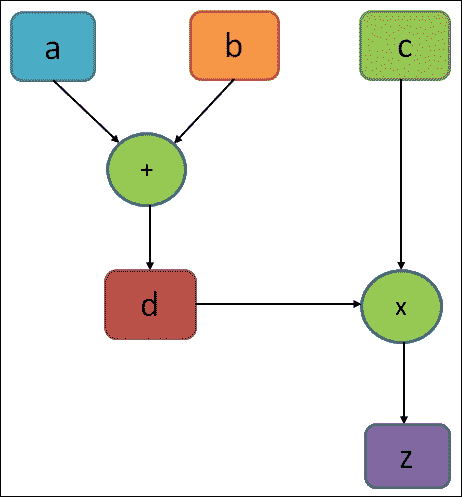圖 2 顯示了簡單計算的計算圖，如`z = d × c = (a + b) × c`：  圖 2：一個計算簡單方程的非常簡單的執行圖 在上圖中，圖中的圓圈表示操作，而矩形表示計算圖。如前所述，TensorFlow 圖包含以下內容： * `tf.Operation`對象：這些是圖中的節點。這些通常簡稱為操作。 操作僅為 TITO（張量 - 張量 - 張量）。一個或多個張量輸入和一個或多個張量輸出。 * `tf.Tensor`對象：這些是圖的邊緣。這些通常簡稱為張量。 張量對象在圖中的各種操作之間流動。在上圖中，`d`也是操作。它可以是“常量”操作，其輸出是張量，包含分配給`d`的實際值。 也可以使用 TensorFlow 執行延遲執行。簡而言之，一旦您在計算圖的構建階段中編寫了高度復合的表達式，您仍然可以在運行會話階段對其進行求值。從技術上講，TensorFlow 安排工作并以??有效的方式按時執行。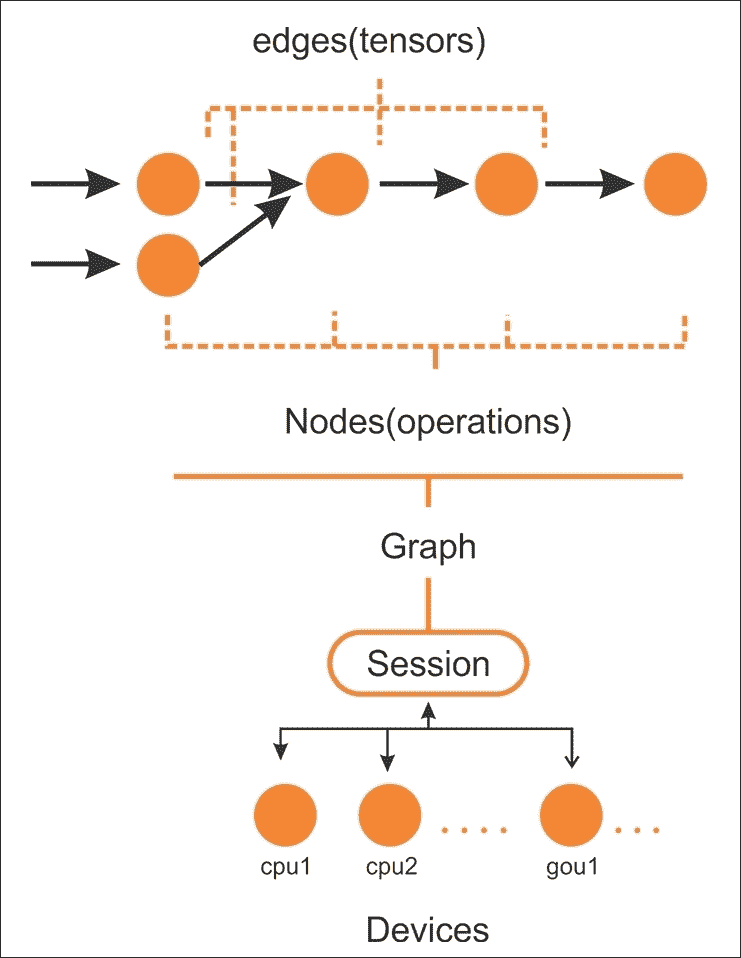 例如，使用 GPU 并行執行代碼的獨立部分如下圖所示：  圖 3：要在 CPU 或 GPU 等設備上的會話上執行的 TensorFlow 圖中的邊和節點 在創建計算圖之后，TensorFlow 需要具有以分布式方式由多個 CPU（以及 GPU，如果可用）執行的活動會話。通常，您實際上不需要明確指定是使用 CPU 還是 GPU，因為 TensorFlow 可以選擇使用哪一個。 默認情況下，將選擇 GPU 以進行盡可能多的操作；否則，將使用 CPU。然而，通常，它會分配所有 GPU 內存，即使它不消耗它。 以下是 TensorFlow 圖的主要組成部分： * 變量：用于 TensorFlow 會話之間的值，包含權重和偏置。 * 張量：一組值，在節點之間傳遞以執行操作（也稱為操作）。 * 占位符：用于在程序和 TensorFlow 圖之間發送數據。 * 會話：當會話啟動時，TensorFlow 會自動計算圖中所有操作的梯度，并在鏈式規則中使用它們。實際上，在執行圖時會調用會話。 不用擔心，前面這些組件中的每一個都將在后面的章節中討論。從技術上講，您將要編寫的程序可以被視為客戶。然后，客戶端用于以符號方式在 C/C++ 或 Python 中創建執行圖，然后您的代碼可以請求 TensorFlow 執行此圖。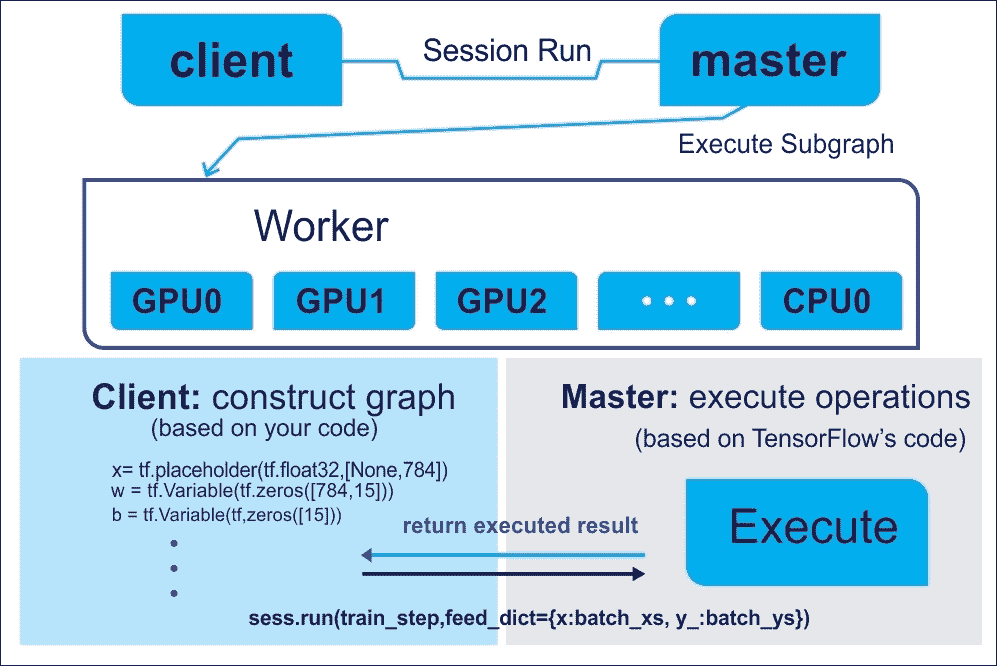整個概念從下圖中變得更加清晰：  圖 4：使用客戶端主架構來執行 TensorFlow 圖 計算圖有助于使用 CPU 或 GPU 在多個計算節點上分配工作負載。這樣，神經網絡可以等同于復合函數，其中每個層（輸入，隱藏或輸出層）可以表示為函數。要了解在張量上執行的操作，需要了解 TensorFlow 編程模型的良好解決方法。 # TensorFlow 代碼結構 TensorFlow 編程模型表示如何構建預測模型。導入 TensorFlow 庫時， TensorFlow 程序通常分為四個階段： * 構建涉及張量運算的計算圖（我們將很快看到張量） * 創建會話 * 運行會話；執行圖中定義的操作 * 執行數據收集和分析 這些主要階段定義了 TensorFlow 中的編程模型。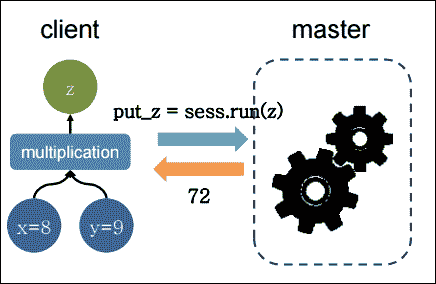請考慮以下示例，其中我們要將兩個數相乘： ```py import tensorflow as tf # Import TensorFlow x = tf.constant(8) # X op y = tf.constant(9) # Y op z = tf.multiply(x, y) # New op Z sess = tf.Session() # Create TensorFlow session out_z = sess.run(z) # execute Z op sess.close() # Close TensorFlow session print('The multiplication of x and y: %d' % out_z)# print result ``` 前面的代碼段可以用下圖表示：  圖 5：在客戶端主架構上執行并返回的簡單乘法 為了使前面的程序更有效，TensorFlow 還允許通過占位符交換圖??變量中的數據（稍后討論）。現在想象一下代碼段之后的可以做同樣的事情，但效率更高： ```py import tensorflow as tf # Build a graph and create session passing the graph with tf.Session() as sess: x = tf.placeholder(tf.float32, name="x") y = tf.placeholder(tf.float32, name="y") z = tf.multiply(x,y) # Put the values 8,9 on the placeholders x,y and execute the graph z_output = sess.run(z,feed_dict={x: 8, y:9}) print(z_output) ``` TensorFlow 不是乘以兩個數字所必需的。此外，這個簡單的操作有很多行代碼。該示例的目的是闡明如何構造代碼，從最簡單的（如在本例中）到最復雜的。此外，該示例還包含一些基本指令，我們將在本書中給出的所有其他示例中找到這些指令。 第一行中的單個導入為您的命令導入 TensorFlow;如前所述，它可以用`tf`實例化。然后，TensorFlow 運算符將由`tf`和要使用的運算符的名稱表示。在下一行中，我們通過`tf.Session()`指令構造`session`對象： ```py with tf.Session() as sess: ``` ### 提示 會話對象（即`sess`）封裝了 TensorFlow 的環境，以便執行所有操作對象，并求值`Tensor`對象。我們將在接下來的部分中看到它們。 該對象包含計算圖，如前所述，它包含要執行的計算。以下兩行使用`placeholder`定義變量`x`和`y`。通過`placeholder`，您可以定義輸入（例如我們示例的變量`x`）和輸出變量（例如變量`y`）： ```py x = tf.placeholder(tf.float32, name="x") y = tf.placeholder(tf.float32, name="y") ``` ### 提示 占位符提供圖元素和問題計算數據之間的接口。它們允許我們創建我們的操作并構建我們的計算圖而不需要數據，而不是使用它的引用。 要通過`placeholder`函數定義數據或張量（我們將很快向您介紹張量的概念），需要三個參數： * 數據類型是要定義的張量中的元素類型。 * 占位符的形狀是要進給的張量的形狀（可選）。如果未指定形狀，則可以提供任何形狀的張量。 * 名稱對于調試和代碼分析非常有用，但它是可選的。 ### 注意 有關張量的更多信息，請參閱[此鏈接](https://www.tensorflow.org/api_docs/python/tf/Tensor)。 因此，我們可以使用先前定義的兩個參數（占位符和常量）來引入我們想要計算的模型。接下來，我們定義計算模型。 會話內的以下語句構建`x`和`y`的乘積的數據結構，并隨后將操作結果分配給張量`z`。然后它如下： ```py z = tf.multiply(x, y) ``` 由于結果已由占位符`z`保存，我們通過`sess.run`語句執行圖。在這里，我們提供兩個值來將張量修補為圖節點。它暫時用張量值替換操作的輸出： ```py z_output = sess.run(z,feed_dict={x: 8, y:9}) ``` 在最后的指令中，我們打印結果： ```py print(z_output) ``` 這打印輸出`72.0`。 ## 用 TensorFlow 急切執行 如前所述，在啟用 TensorFlow 的急切執行時，我們可以立即執行 TensorFlow 操作，因為它們是以命令方式從 Python 調用的。 啟用急切執行后，TensorFlow 函數會立即執行操作并返回具體值。這與[`tf.Session`](https://www.tensorflow.org/versions/master/api_docs/python/tf/Session)相反，函數添加到圖并創建計算圖中的節點的符號引用。 TensorFlow 通過`tf.enable_eager_execution`提供急切執行的功能，其中包含以下別名： * `tf.contrib.eager.enable_eager_execution` * `tf.enable_eager_execution` `tf.enable_eager_execution`具有以下簽名： ```py tf.enable_eager_execution( config=None, device_policy=None ) ``` 在上面的簽名中，`config`是`tf.ConfigProto`，用于配置執行操作的環境，但這是一個可選參數。另一方面，`device_policy`也是一個可選參數，用于控制關于特定設備（例如 GPU0）上需要輸入的操作如何處理不同設備（例如，GPU1 或 CPU）上的輸入的策略。 現在調用前面的代碼將啟用程序生命周期的急切執行。例如，以下代碼在 TensorFlow 中執行簡單的乘法運算： ```py import tensorflow as tf x = tf.placeholder(tf.float32, shape=[1, 1]) # a placeholder for variable x y = tf.placeholder(tf.float32, shape=[1, 1]) # a placeholder for variable y m = tf.matmul(x, y) with tf.Session() as sess: print(sess.run(m, feed_dict={x: [[2.]], y: [[4.]]})) ``` 以下是上述代碼的輸出： ```py >>> 8. ``` 然而，使用急切執行，整體代碼看起來更簡單： ```py import tensorflow as tf # Eager execution (from TF v1.7 onwards): tf.eager.enable_eager_execution() x = [[2.]] y = [[4.]] m = tf.matmul(x, y) print(m) ``` 以下是上述代碼的輸出： ```py >>> tf.Tensor([[8.]], shape=(1, 1), dtype=float32) ``` 你能理解在執行前面的代碼塊時會發生什么嗎？好了，在啟用了執行后，操作在定義時執行，`Tensor`對象保存具體值，可以通過`numpy()`方法作為`numpy.ndarray`訪問。 請注意，在使用 TensorFlow API 創建或執行圖后，無法啟用急切執行。通常建議在程序啟動時調用此函數，而不是在庫中調用。雖然這聽起來很吸引人，但我們不會在即將到來的章節中使用此功能，因為這是一個新功能，尚未得到很好的探索。 # TensorFlow 中的數據模型 TensorFlow 中的數據模型由張量表示。在不使用復雜的數學定義的情況下，我們可以說張量（在 TensorFlow 中）識別多維數值數組。我們將在下一小節中看到有關張量的更多細節。 ## 張量 讓我們看一下來自[維基百科：張量](https://en.wikipedia.org/wiki/Tensor)的形式定義： > “張量是描述幾何向量，標量和其他張量之間線性關系的幾何對象。這種關系的基本例子包括點積，叉積和線性映射。幾何向量，通常用于物理和工程應用，以及標量他們自己也是張量。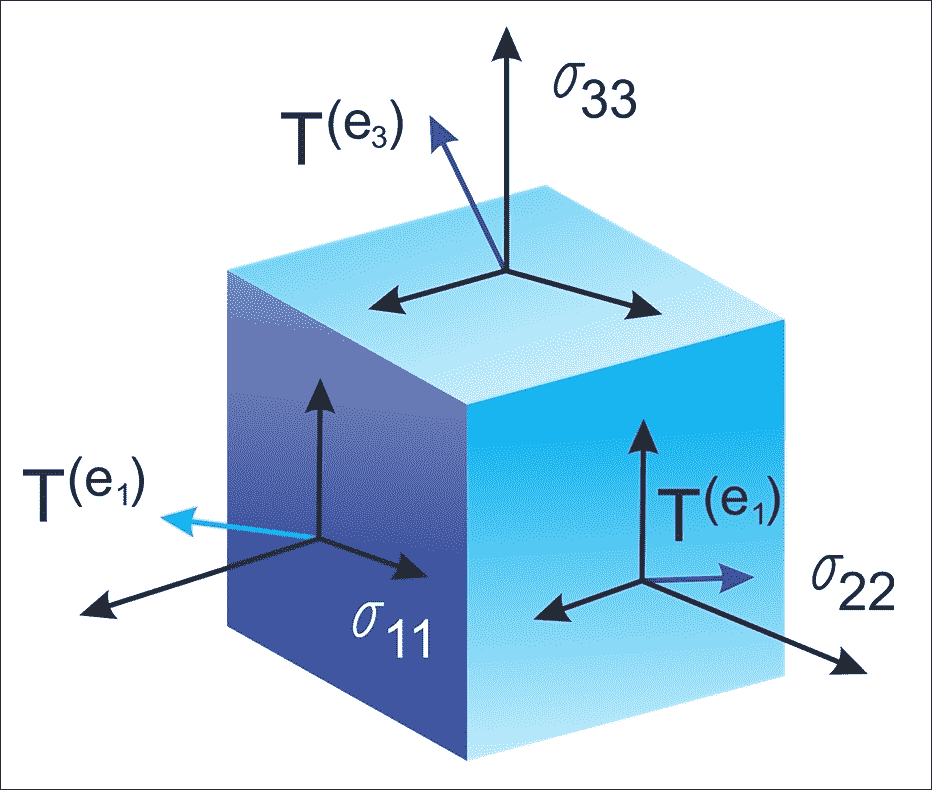“ 該數據結構的特征在于三個參數：秩，形狀和類型，如下圖所示：  圖 6：張量只是具有形狀，階數和類型的幾何對象，用于保存多維數組 因此，張量可以被認為是指定具有任意數量的索引的元素的矩陣的推廣。張量的語法與嵌套向量大致相同。 ### 提示 張量只定義此值的類型以及在會話期間應計算此值的方法。因此，它們不代表或保留操作產生的任何值。 有些人喜歡比較 NumPy 和 TensorFlow。然而，實際上，TensorFlow 和 NumPy 在兩者都是 Nd 數組庫的意義上非常相似！ 嗯，NumPy 確實有 n 維數組支持，但它不提供方法來創建張量函數并自動計算導數（并且它沒有 GPU 支持）。下圖是 NumPy 和 TensorFlow 的簡短一對一比較：  圖 7：NumPy 與 TensorFlow：一對一比較 現在讓我們看一下在 TensorFlow 圖之前創建張量的替代方法（我們將在后面看到其他的進給機制）： ```py >>> X = [[2.0, 4.0], [6.0, 8.0]] # X is a list of lists >>> Y = np.array([[2.0, 4.0], [6.0, 6.0]], dtype=np.float32)#Y is a Numpy array >>> Z = tf.constant([[2.0, 4.0], [6.0, 8.0]]) # Z is a tensor ``` 這里，`X`是列表，`Y`是來自 NumPy 庫的 n 維數組，`Z`是 TensorFlow 張量對象。現在讓我們看看他們的類型： ```py >>> print(type(X)) >>> print(type(Y)) >>> print(type(Z)) #Output <class 'list'> <class 'numpy.ndarray'> <class 'tensorflow.python.framework.ops.Tensor'> ``` 好吧，他們的類型打印正確。但是，與其他類型相比，我們正式處理張量的更方便的函數是`tf.convert_to_tensor()`函數如下： ```py t1 = tf.convert_to_tensor(X, dtype=tf.float32) t2 = tf.convert_to_tensor(Z, dtype=tf.float32) ``` 現在讓我們使用以下代碼查看它們的類型： ```py >>> print(type(t1)) >>> print(type(t2)) #Output: <class 'tensorflow.python.framework.ops.Tensor'> <class 'tensorflow.python.framework.ops.Tensor'> ``` 太棒了！關于張量的討論已經足夠了。因此，我們可以考慮以術語秩為特征的結構。 ## 秩和形狀 稱為秩的維度單位描述每個張量。它識別張量的維數。因此，秩被稱為張量的階數或維度。階數零張量是標量，階數 1 張量是向量，階數 2 張量是矩陣。 以下代碼定義了 TensorFlow `scalar`，`vector`，`matrix`和`cube_matrix`。在下一個示例中，我們將展示秩如何工作： ```py import tensorflow as tf scalar = tf.constant(100) vector = tf.constant([1,2,3,4,5]) matrix = tf.constant([[1,2,3],[4,5,6]]) cube_matrix = tf.constant([[[1],[2],[3]],[[4],[5],[6]],[[7],[8],[9]]]) print(scalar.get_shape()) print(vector.get_shape()) print(matrix.get_shape()) print(cube_matrix.get_shape()) ``` 結果打印在這里： ```py >>> () (5,) (2, 3) (3, 3, 1) >>> ``` 張量的形狀是它具有的行數和列數。現在我們將看看如何將張量的形狀與其階數聯系起來： ```py >>scalar.get_shape() TensorShape([]) >>vector.get_shape() TensorShape([Dimension(5)]) >>matrix.get_shape() TensorShape([Dimension(2), Dimension(3)]) >>cube.get_shape() TensorShape([Dimension(3), Dimension(3), Dimension(1)]) ``` ## 數據類型 除了階數和形狀，張量具有數據類型。以下是數據類型列表： | 數據類型 | Python 類型 | 描述 | | --- | --- | --- | | `DT_FLOAT` | `tf.float32` | 32 位浮點 | | `DT_DOUBLE` | `tf.float64` | 64 位浮點 | | `DT_INT8` | `tf.int8` | 8 位有符號整數 | | `DT_INT16` | `tf.int16` | 16 位有符號整數 | | `DT_INT32` | `tf.int32` | 32 位有符號整數 | | `DT_INT64` | `tf.int64` | 64 位有符號整數 | | `DT_UINT8` | `tf.uint8` | 8 位無符號整數 | | `DT_STRING` | `tf.string` | 可變長度字節數組。張量的每個元素都是一個字節數組 | | `DT_BOOL` | `tf.bool` | 布爾 | | `DT_COMPLEX64` | `tf.complex64` | 由兩個 32 位浮點組成的復數：實部和虛部 | | `DT_COMPLEX128` | `tf.complex128` | 由兩個 64 位浮點組成的復數：實部和虛部 | | `DT_QINT8` | `tf.qint8` | 量化操作中使用的 8 位有符號整數 | | `DT_QINT32` | `tf.qint32` | 量化操作中使用的 32 位有符號整數 | | `DT_QUINT8` | `tf.quint8` | 量化操作中使用的 8 位無符號整數 | 上表是不言自明的，因此我們沒有提供有關數據類型的詳細討論。 TensorFlow API 用于管理與 NumPy 數組之間的數據。 因此，要構建具有常量值的張量，將 NumPy 數組傳遞給`tf.constant()`運算符，結果將是具有該值的張量： ```py import tensorflow as tf import numpy as np array_1d = np.array([1,2,3,4,5,6,7,8,9,10]) tensor_1d = tf.constant(array_1d) with tf.Session() as sess: print(tensor_1d.get_shape()) print(sess.run(tensor_1d)) ``` 運行該示例，我們獲得以下內容： ```py >>> (10,) [ 1 2 3 4 5 6 7 8 9 10] ``` 要構建具有變量值的張量，請使用 NumPy 數組并將其傳遞給`tf.Variable`構造器。結果將是具有該初始值的變量張量： ```py import tensorflow as tf import numpy as np # Create a sample NumPy array array_2d = np.array([(1,2,3),(4,5,6),(7,8,9)]) # Now pass the preceding array to tf.Variable() tensor_2d = tf.Variable(array_2d) # Execute the preceding op under an active session with tf.Session() as sess: sess.run(tf.global_variables_initializer()) print(tensor_2d.get_shape()) print sess.run(tensor_2d) # Finally, close the TensorFlow session when you're done sess.close() ``` 在前面的代碼塊中，`tf.global_variables_initializer()`用于初始化我們之前創建的所有操作。如果需要創建一個初始值取決于另一個變量的變量，請使用另一個變量的`initialized_value()`。這可確保以正確的順序初始化變量。 結果如下： ```py >>> (3, 3) [[1 2 3] [4 5 6] [7 8 9]] ``` 為了便于在交互式 Python 環境中使用，我們可以使用`InteractiveSession`類，然后將該會話用于所有`Tensor.eval()`和`Operation.run()`調用： ```py import tensorflow as tf # Import TensorFlow import numpy as np # Import numpy # Create an interactive TensorFlow session interactive_session = tf.InteractiveSession() # Create a 1d NumPy array array1 = np.array([1,2,3,4,5]) # An array # Then convert the preceding array into a tensor tensor = tf.constant(array1) # convert to tensor print(tensor.eval()) # evaluate the tensor op interactive_session.close() # close the session ``` ### 提示 `tf.InteractiveSession()`只是方便的語法糖，用于在 IPython 中保持默認會話打開。 結果如下： ```py >>> [1 2 3 4 5] ``` 在交互式設置中，例如 shell 或 IPython 筆記本，這可能會更容易，因為在任何地方傳遞會話對象都很繁瑣。 ### 注意 IPython 筆記本現在稱為 Jupyter 筆記本。它是一個交互式計算環境，您可以在其中組合代碼執行，富文本，數學，繪圖和富媒體。有關更多信息，感興趣的讀者請參閱[此鏈接](https://ipython.org/notebook.html)。 定義張量的另一種方法是使用`tf.convert_to_tensor`語句： ```py import tensorflow as tf import numpy as np tensor_3d = np.array([[[0, 1, 2], [3, 4, 5], [6, 7, 8]], [[9, 10, 11], [12, 13, 14], [15, 16, 17]], [[18, 19, 20], [21, 22, 23], [24, 25, 26]]]) tensor_3d = tf.convert_to_tensor(tensor_3d, dtype=tf.float64) with tf.Session() as sess: print(tensor_3d.get_shape()) print(sess.run(tensor_3d)) # Finally, close the TensorFlow session when you're done sess.close() ``` 以下是上述代碼的輸出： ```py >>> (3, 3, 3) [[[ 0\. 1\. 2.] [ 3\. 4\. 5.] [ 6\. 7\. 8.]] [[ 9\. 10\. 11.] [ 12\. 13\. 14.] [ 15\. 16\. 17.]] [[ 18\. 19\. 20.] [ 21\. 22\. 23.] [ 24\. 25\. 26.]]] ``` ## 變量 變量是用于保存和更新參數的 TensorFlow 對象。必須初始化變量，以便您可以保存并恢復它以便稍后分析代碼。使用`tf.Variable()`或`tf.get_variable()`語句創建變量。而`tf.get_varaiable()`被推薦但`tf.Variable()`是低標簽抽象。 在下面的示例中，我們要計算從 1 到 10 的數字，但讓我們先導入 TensorFlow： ```py import tensorflow as tf ``` 我們創建了一個將初始化為標量值 0 的變量： ```py value = tf.get_variable("value", shape=[], dtype=tf.int32, initializer=None, regularizer=None, trainable=True, collections=None) ``` `assign()`和`add()`運算符只是計算圖的節點，因此在會話運行之前它們不會執行賦值： ```py one = tf.constant(1) update_value = tf.assign_add(value, one) initialize_var = tf.global_variables_initializer() ``` 我們可以實例化計算圖： ```py with tf.Session() as sess: sess.run(initialize_var) print(sess.run(value)) for _ in range(5): sess.run(update_value) print(sess.run(value)) # Close the session ``` 讓我們回想一下，張量對象是操作結果的符號句柄，但它實際上并不保存操作輸出的值： ```py >>> 0 1 2 3 4 5 ``` ## 運行 要獲取操作的輸出，可以通過調用會話對象上的`run()`并傳入張量來執行圖。除了獲取單個張量節點，您還可以獲取多個張量。 在下面的示例中，使用`run()`調用一起提取`sum`和`multiply`張量： ```py import tensorflow as tf constant_A = tf.constant([100.0]) constant_B = tf.constant([300.0]) constant_C = tf.constant([3.0]) sum_ = tf.add(constant_A,constant_B) mul_ = tf.multiply(constant_A,constant_C) with tf.Session() as sess: result = sess.run([sum_,mul_])# _ means throw away afterwards print(result) ``` 輸出如下： ```py >>> [array(400.],dtype=float32),array([ 300.],dtype=float32)] ``` 應該注意的是，所有需要執行的操作（即，為了產生張量值）都運行一次（每個請求的張量不是一次）。 ## 饋送和占位符 有四種方法將數據輸入 TensorFlow 程序（更多信息，請參閱[此鏈接](https://www.tensorflow.org/api_guides/python/reading_data)）： * 數據集 API：這使您能夠從簡單和可重用的分布式文件系統構建復雜的輸入管道，并執行復雜的操作。如果您要處理不同數據格式的大量數據，建議使用數據集 API。數據集 API 為 TensorFlow 引入了兩個新的抽象，用于創建可饋送數據集：`tf.contrib.data.Dataset`（通過創建源或應用轉換操作）和`tf.contrib.data.Iterator`。 * 饋送：這允許我們將數據注入計算圖中的任何張量。 * 從文件中讀取：這允許我們使用 Python 的內置機制開發輸入管道，用于從圖開頭的數據文件中讀取數據。 * 預加載數據：對于小數據集，我們可以使用 TensorFlow 圖中的常量或變量來保存所有數據。 在本節中，我們將看到饋送機制的例子。我們將在接下來的章節中看到其他方法。 TensorFlow 提供了一種饋送機制，允許我們將數據注入計算圖中的任何張量。您可以通過`feed_dict`參數將源數據提供給啟動計算的`run()`或`eval()`調用。 ### 提示 使用`feed_dict`參數進行饋送是將數據提供到 TensorFlow 執行圖中的最低效方法，并且僅應用于需要小數據集的小型實驗。它也可以用于調試。 我們還可以用饋送數據（即變量和常量）替換任何張量。最佳做法是使用[`tf.placeholder()`](https://www.tensorflow.org/api_docs/python/tf/placeholder)使用 TensorFlow 占位符節點。占位符專門用作饋送的目標。空占位符未初始化，因此不包含任何數據。 因此，如果在沒有饋送的情況下執行它，它將始終生成錯誤，因此您不會忘記提供它。以下示例顯示如何提供數據以構建隨機`2×3`矩陣： ```py import tensorflow as tf import numpy as np a = 3 b = 2 x = tf.placeholder(tf.float32,shape=(a,b)) y = tf.add(x,x) data = np.random.rand(a,b) sess = tf.Session() print(sess.run(y,feed_dict={x:data})) sess.close()# close the session ``` 輸出如下： ```py >>> [[ 1.78602004 1.64606333] [ 1.03966308 0.99269408] [ 0.98822606 1.50157797]] >>> ``` # 通過 TensorBoard 可視化計算 TensorFlow 包含函數 ，允許您在名為 TensorBoard 的可視化工具中調試和優化程序。使用 TensorBoard，您可以以圖形方式觀察有關圖任何部分的參數和詳細信息的不同類型的統計數據。 此外，在使用復雜的 DNN 進行預測建模時，圖可能很復雜且令人困惑。為了更容易理解，調試和優化 TensorFlow 程序，您可以使用 TensorBoard 可視化 TensorFlow 圖，繪制有關圖執行的量化指標，并顯示其他數據，例如通過它的圖像。 因此，TensorBoard 可以被認為是一個用于分析和調試預測模型的框架。 TensorBoard 使用所謂的摘要來查看模型的參數：一旦執行了 TensorFlow 代碼，我們就可以調用 TensorBoard 來查看 GUI 中的摘要。 ## TensorBoard 如何運作？ TensorFlow 使用計算圖來執行應用。在計算圖中，節點表示操作，弧是操作之間的數據。 TensorBoard 的主要思想是將摘要與圖上的節點（操作）相關聯。代碼運行時，摘要操作將序列化節點的數據并將數據輸出到文件中。稍后，TensorBoard 將可視化匯總操作。有關更詳細的討論，讀者可以參考[此鏈接](https://github.com/tensorflow/tensorboard)。 簡而言之，TensorBoard 是一套 Web 應用，用于檢查和理解您的 TensorFlow 運行和圖。使用 TensorBoard 時的工作流程如下： 1. 構建計算圖/代碼 2. 將摘要操作附加到您要檢查的節點 3. 像往常一樣開始運行圖 4. 運行摘要操作 5. 執行完成后，運行 TensorBoard 以顯示摘要輸出 ```py file_writer = tf.summary.FileWriter('/path/to/logs', sess.graph) ``` 對于步驟 2（即，在運行 TensorBoard 之前），請確保通過創建摘要編寫器在日志目錄中生成摘要數據： ＃`sess.graph`包含圖定義；啟用圖可視化工具 現在，如果你在終端中鍵入`$ which tensorboard`，如果你用 pip 安裝它，它應該存在： ```py root@ubuntu:~$ which tensorboard /usr/local/bin/tensorboard ``` 你需要給它一個日志目錄。當您在運行圖的目錄中時，可以使用以下內容從終端啟動它： ```py tensorboard --logdir path/to/logs ``` 當 TensorBoard 配置完全時，可以通過發出以下命令來訪問它： ```py # Make sure there's no space before or after '=" $ tensorboard –logdir=<trace_file_name> ``` 現在您只需輸入`http://localhost:6006/`即可從瀏覽器訪問`localhost:6006`。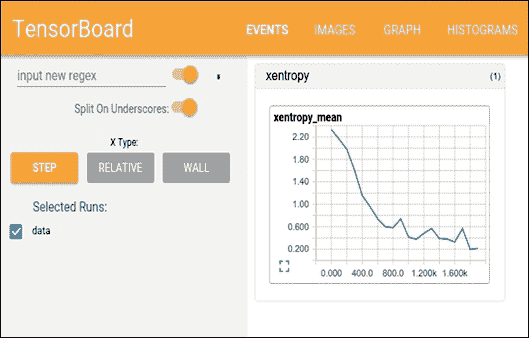然后它應該是這樣的：  圖 8：在瀏覽器上使用 TensorBoard ### 注意 TensorBoard 可用于谷歌瀏覽器或 Firefox。其他瀏覽器可能有效，但可能存在錯誤或表現問題。 這已經太過分了嗎？不要擔心，在上一節中，我們將結合前面解釋的所有想法構建單個輸入神經元模型并使用 TensorBoard 進行分析。 # 線性回歸及更多 在本節中，我們將仔細研究 TensorFlow 和 TensorBoard 的主要概念，并嘗試做一些基本操作來幫助您入門。我們想要實現的模型模擬線性回歸。 在統計和 ML 中，線性回歸是一種經常用于衡量變量之間關系的技術。這是一種非常簡單但有效的算法，也可用于預測建模。 線性回歸模擬因變量`y[i]`，自變量`x[i]`，和隨機項`b`。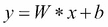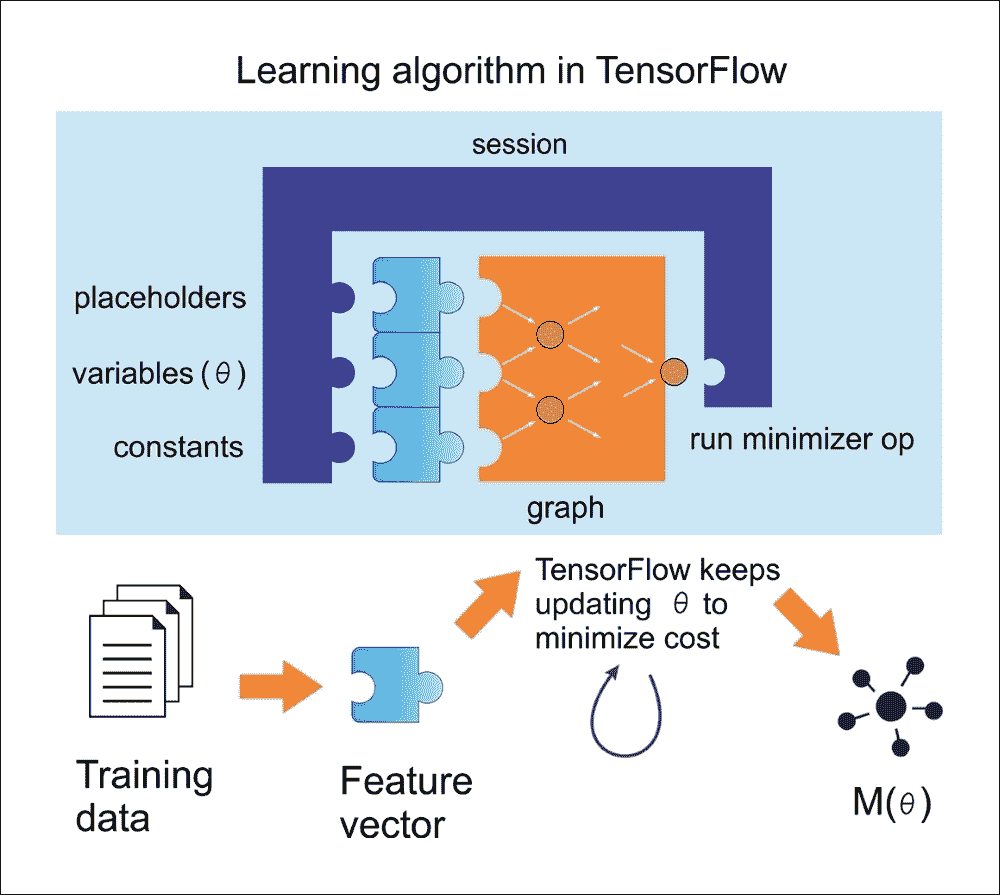這可以看作如下：  使用 TensorFlow 的典型線性回歸問題具有以下工作流程，該工作流程更新參數以最小化給定成本函數（參見下圖）：  圖 9：在 TensorFlow 中使用線性回歸的學習算法 現在，讓我們嘗試按照前面的圖，通過概念化前面的等式將其重現為線性回歸。為此，我們將編寫一個簡單的 Python 程序，用于在 2D 空間中創建數據。然后我們將使用 TensorFlow 來尋找最適合數據點的線（如下圖所示）： ```py # Import libraries (Numpy, matplotlib) import numpy as np import matplotlib.pyplot as plot # Create 1000 points following a function y=0.1 * x + 0.4z (i.e. # y = W * x + b) with some normal random distribution: num_points = 1000 vectors_set = [] # Create a few random data points for i in range(num_points): W = 0.1 # W b = 0.4 # b x1 = np.random.normal(0.0, 1.0)#in: mean, standard deviation nd = np.random.normal(0.0, 0.05)#in:mean,standard deviation y1 = W * x1 + b # Add some impurity with normal distribution -i.e. 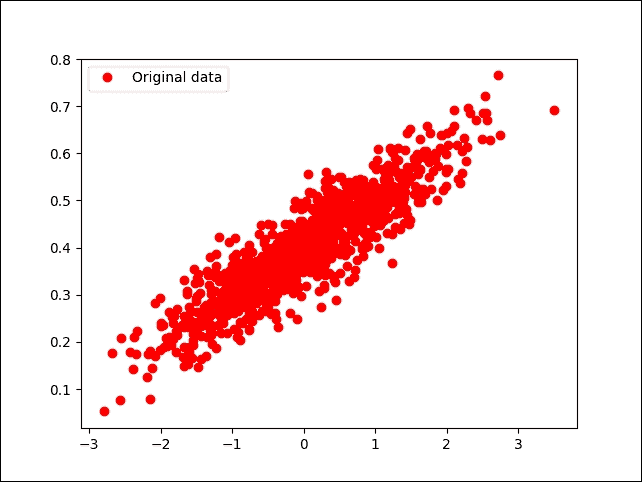nd y1 = y1 + nd # Append them and create a combined vector set: vectors_set.append([x1, y1]) # Separate the data point across axises: x_data = [v[0] for v in vectors_set] y_data = [v[1] for v in vectors_set] # Plot and show the data points in a 2D space plot.plot(x_data, y_data, 'ro', label='Original data') plot.legend() plot.show() ``` 如果您的編譯器沒有報錯，您應該得到以下圖表：  圖 10：隨機生成（但原始）數據 好吧，到目前為止，我們剛剛創建了一些數據點而沒有可以通過 TensorFlow 執行的相關模型。因此，下一步是創建一個線性回歸模型，該模型可以獲得從輸入數據點估計的輸出值`y`，即`x_data`。在這種情況下，我們只有兩個相關參數，`W`和`b`。 現在的目標是創建一個圖，允許我們根據輸入數據`x_data`，通過將它們調整為`y_data`來找到這兩個參數的值。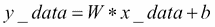因此，我們的目標函數如下：  如果你還記得，我們在 2D 空間中創建數據點時定義了`W = 0.1`和`b = 0.4`。 TensorFlow 必須優化這兩個值，使`W`趨于 0.1 和`b`為 0.4。 解決此類優化問題的標準方法是迭代數據點的每個值并調整`W`和`b`的值，以便為每次迭代獲得更精確的答案。要查看值是否確實在改善，我們需要定義一個成本函數來衡量某條線的優質程度。 在我們的例子中，成本函數是均方誤差，這有助于我們根據實際數據點與每次迭代的估計距離函數之間的距離函數找出誤差的平均值。我們首先導入 TensorFlow 庫： ```py import tensorflow as tf W = tf.Variable(tf.zeros([1])) b = tf.Variable(tf.zeros([1])) y = W * x_data + b ``` 在前面的代碼段中，我們使用不同的策略生成一個隨機點并將其存儲在變量`W`中。現在，讓我們定義一個損失函數`loss = mean[(y - y_data)^2]`，這將返回一個標量值，其中包含我們之間所有距離的均值。數據和模型預測。就 TensorFlow 約定而言，損失函數可表示如下： ```py loss = tf.reduce_mean(tf.square(y - y_data)) ``` 前一行實際上計算均方誤差（MSE）。在不進一步詳述的情況下，我們可以使用一些廣泛使用的優化算法，例如 GD。在最低級別，GD 是一種算法，它對我們已經擁有的一組給定參數起作用。 它以一組初始參數值開始，并迭代地移向一組值，這些值通過采用另一個稱為學習率的參數來最小化函數。通過在梯度函數的負方向上采取步驟來實現這種迭代最小化： ```py optimizer = tf.train.GradientDescentOptimizer(0.6) train = optimizer.minimize(loss) ``` 在運行此優化函數之前，我們需要初始化到目前為止所有的變量。讓我們使用傳統的 TensorFlow 技術，如下所示： ```py init = tf.global_variables_initializer() sess = tf.Session() sess.run(init) ``` 由于我們已經創建了 TensorFlow 會話，我們已準備好進行迭代過程，幫助我們找到`W`和`b`的最佳值： ```py for i in range(6): sess.run(train) print(i, sess.run(W), sess.run(b), sess.run(loss)) ``` 您應該觀察以下輸出： ```py >>> 0 [ 0.18418592] [ 0.47198644] 0.0152888 1 [ 0.08373772] [ 0.38146532] 0.00311204 2 [ 0.10470386] [ 0.39876288] 0.00262051 3 [ 0.10031486] [ 0.39547175] 0.00260051 4 [ 0.10123629] [ 0.39609471] 0.00259969 5 [ 0.1010423] [ 0.39597753] 0.00259966 6 [ 0.10108326] [ 0.3959994] 0.00259966 7 [ 0.10107458] [ 0.39599535] 0.00259966 ``` 你可以看到算法從`W = 0.18418592`和`b = 0.47198644`的初始值開始，損失非常高。然后，算法通過最小化成本函數來迭代地調整值。在第八次迭代中，所有值都傾向于我們期望的值。 現在，如果我們可以繪制它們怎么辦？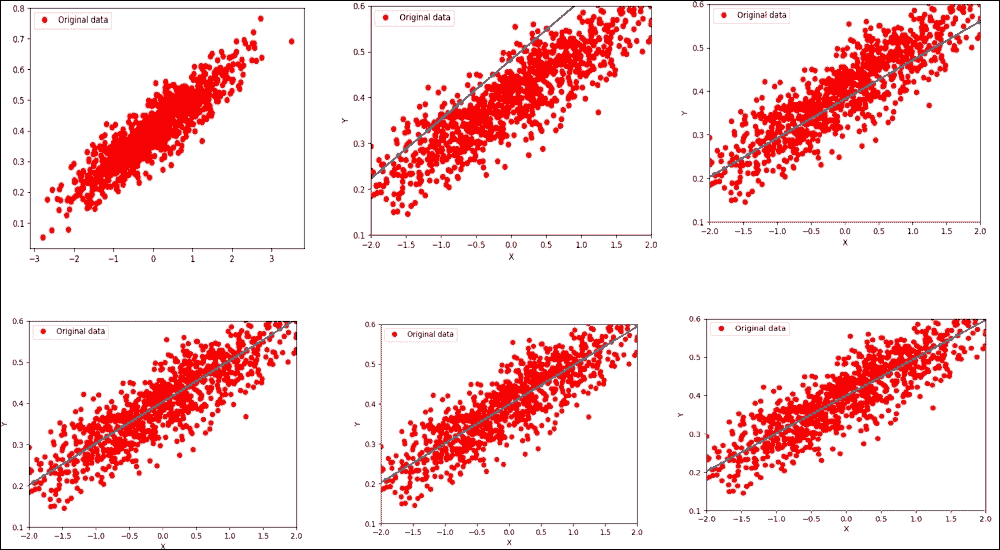讓我們通過在`for`循環下添加繪圖線來實現 ，如下所示： ```py for i in range(6): sess.run(train) print(i, sess.run(W), sess.run(b), sess.run(loss)) plot.plot(x_data, y_data, 'ro', label='Original data') plot.plot(x_data, sess.run(W)*x_data + sess.run(b)) plot.xlabel('X') plot.xlim(-2, 2) plot.ylim(0.1, 0.6) plot.ylabel('Y') plot.legend() plot.show() ``` 前面的代碼塊應該生成下圖（雖然合并在一起）：  圖 11：在第六次迭代后優化損失函數的線性回歸 現在讓我們進入第 16 次迭代： ```py >>> 0 [ 0.23306453] [ 0.47967502] 0.0259004 1 [ 0.08183448] [ 0.38200468] 0.00311023 2 [ 0.10253634] [ 0.40177572] 0.00254209 3 [ 0.09969243] [ 0.39778906] 0.0025257 4 [ 0.10008509] [ 0.39859086] 0.00252516 5 [ 0.10003048] [ 0.39842987] 0.00252514 6 [ 0.10003816] [ 0.39846218] 0.00252514 7 [ 0.10003706] [ 0.39845571] 0.00252514 8 [ 0.10003722] [ 0.39845699] 0.00252514 9 [ 0.10003719] [ 0.39845672] 0.00252514 10 [ 0.1000372] [ 0.39845678] 0.00252514 11 [ 0.1000372] [ 0.39845678] 0.00252514 12 [ 0.1000372] [ 0.39845678] 0.00252514 13 [ 0.1000372] [ 0.39845678] 0.00252514 14 [ 0.1000372] [ 0.39845678] 0.00252514 15 [ 0.1000372] [ 0.39845678] 0.00252514 ``` 好多了，我們更接近優化的值，對吧？現在，如果我們通過 TensorFlow 進一步改進我們的可視化分析，以幫助可視化這些圖中發生的事情，該怎么辦？ TensorBoard 提供了一個網頁，用于調試圖并檢查變量，節點，邊緣及其相應的連接。 此外，我們需要使用變量標注前面的圖，例如損失函數，`W`，`b`，`y_data`，`x_data`等。然后，您需要通過調用`tf.summary.merge_all()`函數生成所有摘要。 現在，我們需要對前面的代碼進行如下更改。但是，最好使用`tf.name_scope()`函數對圖上的相關節點進行分組。因此，我們可以使用`tf.name_scope()`來組織 TensorBoard 圖表視圖中的內容，但讓我們給它一個更好的名稱： ```py with tf.name_scope("LinearRegression") as scope: W = tf.Variable(tf.zeros([1])) b = tf.Variable(tf.zeros([1])) y = W * x_data + b ``` 然后，讓我們以類似的方式標注損失函數，但使用合適的名稱，例如`LossFunction`： ```py with tf.name_scope("LossFunction") as scope: loss = tf.reduce_mean(tf.square(y - y_data)) ``` 讓我們標注 TensorBoard 所需的損失，權重和偏置： ```py loss_summary = tf.summary.scalar("loss", loss) w_ = tf.summary.histogram("W", W) b_ = tf.summary.histogram("b", b) ``` 一旦您標注了圖，就可以通過合并來配置摘要了： ```py merged_op = tf.summary.merge_all() ``` 在運行訓練之前（初始化之后），使用`tf.summary.FileWriter()` API 編寫摘要，如下所示： ```py writer_tensorboard = tf.summary.FileWriter('logs/', tf.get_default_graph()) ``` 然后按如下方式啟動 TensorBoard： ```py $ tensorboard –logdir=<trace_dir_name> ``` 在我們的例子中，它可能類似于以下內容： ```py $ tensorboard --logdir=/home/root/LR/ ``` 現在讓我們轉到`http://localhost:6006`并單擊 GRAPH 選項卡。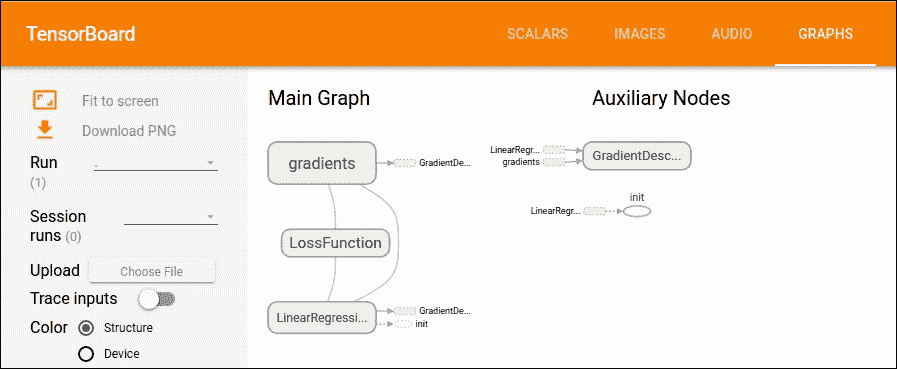您應該看到以下圖表：  圖 12：TensorBoard 上的主圖和輔助節點 ### 提示 請注意，Ubuntu 可能會要求您安裝`python-tk`包。您可以通過在 Ubuntu 上執行以下命令來執行此操作： ```py $ sudo apt-get install python-tk # For Python 3.x, use the following $ sudo apt-get install python3-tk ``` ## 真實數據集的線性回歸回顧 在上一節中，我們看到線性回歸的一個例子。我們看到了如何將 TensorFlow 與隨機生成的數據集一起使用，即假數據。我們已經看到回歸是一種用于預測連續（而非離散）輸出的監督機器學習。 然而，對假數據進行線性回歸就像買一輛新車但從不開車。這個令人敬畏的機器需要在現實世界中使用！幸運的是，許多數據集可在線獲取，以測試您新發現的回歸知識。 其中一個是波士頓住房數據集，可以從 [UCI 機器學習庫](https://archive.ics.uci.edu/ml/datasets/Housing)下載。它也可以作為 scikit-learn 的預處理數據集使用。 所以，讓我們開始導入所有必需的庫，包括 TensorFlow，NumPy，Matplotlib 和 scikit-learn： ```py import matplotlib.pyplot as plt import tensorflow as tf import numpy as np from numpy import genfromtxt from sklearn.datasets import load_boston from sklearn.model_selection import train_test_split ``` 接下來，我們需要準備由波士頓住房數據集中的特征和標簽組成的訓練集。`read_boston_data ()`方法從 scikit-learn 讀取并分別返回特征和標簽： ```py def read_boston_data(): boston = load_boston() features = np.array(boston.data) labels = np.array(boston.target) return features, labels ``` 現在我們已經擁有特征和標簽，我們還需要使用`normalizer()`方法對特征進行標準化。這是方法的簽名： ```py def normalizer(dataset): mu = np.mean(dataset,axis=0) sigma = np.std(dataset,axis=0) return(dataset - mu)/sigma ``` `bias_vector()`用于將偏差項（即全 1）附加到我們在前一步驟中準備的標準化特征。它對應于前一個例子中直線方程中的`b`項： ```py def bias_vector(features,labels): n_training_samples = features.shape[0] n_dim = features.shape[1] f = np.reshape(np.c_[np.ones(n_training_samples),features],[n_training_samples,n_dim + 1]) l = np.reshape(labels,[n_training_samples,1]) return f, l ``` 我們現在將調用這些方法并將數據集拆分為訓練和測試，75% 用于訓練和休息用于測試： ```py features,labels = read_boston_data() normalized_features = normalizer(features) data, label = bias_vector(normalized_features,labels) n_dim = data.shape[1] # Train-test split train_x, test_x, train_y, test_y = train_test_split(data,label,test_size = 0.25,random_state = 100) ``` 現在讓我們使用 TensorFlow 的數據結構（例如占位符，標簽和權重）： ```py learning_rate = 0.01 training_epochs = 100000 log_loss = np.empty(shape=[1],dtype=float) X = tf.placeholder(tf.float32,[None,n_dim]) #takes any number of rows but n_dim columns Y = tf.placeholder(tf.float32,[None,1]) # #takes any number of rows but only 1 continuous column W = tf.Variable(tf.ones([n_dim,1])) # W weight vector ``` 做得好！我們已經準備好構建 TensorFlow 圖所需的數據結構。現在是構建線性回歸的時候了，這非常簡單： ```py y_ = tf.matmul(X, W) cost_op = tf.reduce_mean(tf.square(y_ - Y)) training_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost_op) ``` 在前面的代碼段中，第一行將特征矩陣乘以可用于預測的權重矩陣。第二行計算損失，即回歸線的平方誤差。最后，第三行執行 GD 優化的一步以最小化平方誤差。 ### 提示 使用哪種優化器：使用優化器的主要目的是最小化成本；因此，我們必須定義一個優化器。使用最常見的優化器（如 SGD），學習率必須以`1 / T`進行縮放才能獲得收斂，其中`T`是迭代次數。 Adam 或 RMSProp 嘗試通過調整步長來自動克服此限制，以使步長與梯度具有相同的比例。此外，在前面的示例中，我們使用了 Adam 優化器，它在大多數情況下都表現良好。 然而，如果您正在訓練神經網絡計算梯度是必須的，使用實現 RMSProp 算法的`RMSPropOptimizer`函數是一個更好的主意，因為它是在小批量設置中學習的更快的方式。研究人員還建議在訓練深度 CNN 或 DNN 時使用 Momentum 優化器。 從技術上講，RMSPropOptimizer 是一種先進的梯度下降形式，它將學習率除以指數衰減的平方梯度平均值。衰減參數的建議設置值為 0.9，而學習率的良好默認值為 0.001。 例如在 TensorFlow 中，`tf.train.RMSPropOptimizer()`幫助我們輕松使用它： ```py optimizer = tf.train.RMSPropOptimizer(0.001, 0.9).minimize(cost_op) ``` 現在，在我們開始訓練模型之前，我們需要使用`initialize_all_variables()`方法初始化所有變量，如下所示： ```py init = tf.initialize_all_variables() ``` 太棒了！現在我們已經設法準備好所有組件，我們已經準備好訓練實際的訓練了。我們首先創建 TensorFlow 會話，如下所示： ```py sess = tf.Session() sess.run(init_op) for epoch in range(training_epochs): sess.run(training_step,feed_dict={X:train_x,Y:train_y}) log_loss = np.append(log_loss,sess.run(cost_op,feed_dict={X: train_x,Y: train_y})) ``` 訓練完成后，我們就可以對看不見的數據進行預測。然而，看到完成訓練的直觀表示會更令人興奮。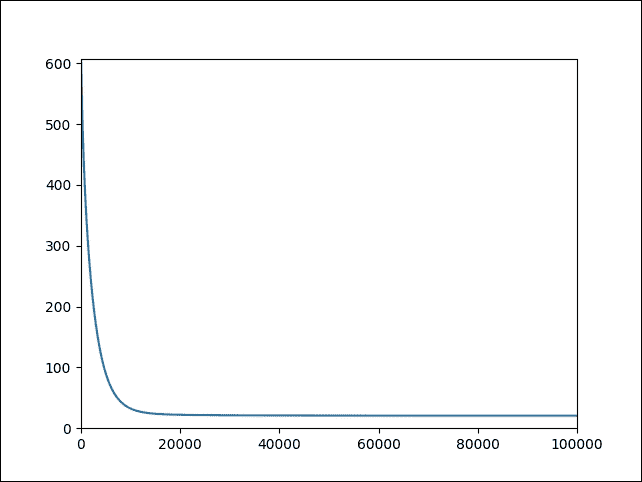因此，讓我們使用 Matplotlib 將成本繪制為迭代次數的函數： ```py plt.plot(range(len(log_loss)),log_loss) plt.axis([0,training_epochs,0,np.max(log_loss)]) plt.show() ``` 以下是上述代碼的輸出： ```py >>> ```  圖 13：作為迭代次數函數的成本 對測試數據集做一些預測并計算均方誤差： ```py pred_y = sess.run(y_, feed_dict={X: test_x}) mse = tf.reduce_mean(tf.square(pred_y - test_y)) print("MSE: %.4f" % sess.run(mse)) ``` 以下是上述代碼的輸出： ```py >>> MSE: 27.3749 ``` 最后，讓我們展示最佳擬合線： ```py fig, ax = plt.subplots() ax.scatter(test_y, pred_y) ax.plot([test_y.min(), test_y.max()], [test_y.min(), test_y.max()], 'k--', lw=3) ax.set_xlabel('Measured') ax.set_ylabel('Predicted') plt.show() ``` 以下是上述代碼的輸出： ```py >>> ```  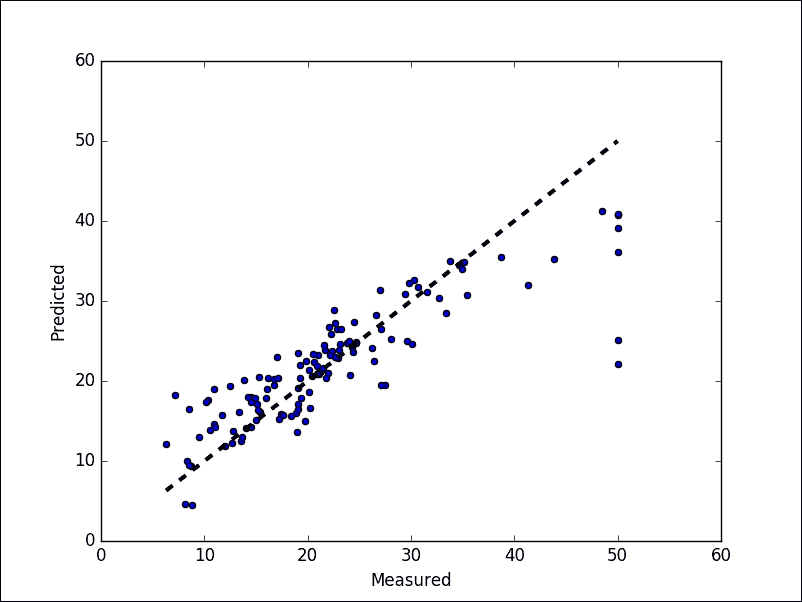圖 14：預測值與實際值 # 總結 TensorFlow 旨在通過 ML 和 DL 輕松地為每個人進行預測分析，但使用它確實需要對一些通用原則和算法有一個正確的理解。 TensorFlow 的最新版本帶有許多令人興奮的新功能，所以我們試圖覆蓋它們，以便您可以輕松使用它們。總之，這里簡要回顧一下本章已經解釋過的 TensorFlow 的關鍵概念： * 圖：每個 TensorFlow 計算可以表示為數據流圖，其中每個圖構建為一組操作對象。有三種核心圖數據結構：[`tf.Graph`](https://www.tensorflow.org/api_docs/python/tf/Graph)，[`tf.Operation`](https://www.tensorflow.org/api_docs/python/tf/Operation)和[`tf.Tensor`](https://www.tensorflow.org/api_docs/python/tf/Tensor) ）。 * 操作：圖節點將一個或多個張量作為輸入，并產生一個或多個張量作為輸出。節點可以由操作對象表示，用于執行諸如加法，乘法，除法，減法或更復雜操作的計算單元。 * 張量：它們就像高維數組對象。換句話說，它們可以表示為數據流圖的邊緣，并且是不同操作的輸出。 * 會話：會話對象是一個實體，它封裝了執行操作對象的環境，以便在數據流圖上運行計算。結果，在`run()`或`eval()`調用內部求值張量對象。 在本章的后面部分，我們介紹了 TensorBoard，它是分析和調試神經網絡模型的強大工具。最后，我們看到了如何在假數據集和真實數據集上實現最簡單的基于 TensorFlow 的線性回歸模型之一。 在下一章中，我們將討論不同 FFNN 架構的理論背景，如深度信念網絡（DBN）和多層感知器（MLP）。 然后，我們將展示如何訓練和分析評估模型所需的表現指標，然后通過一些方法調整 FFNN 的超參數以優化表現。最后，我們將提供兩個使用 MLP 和 DBN 的示例，說明如何為銀行營銷數據集建立非常強大和準確的預測分析模型。