# 四、神經網絡簡介 在本章中，我們將介紹以下主題： * 什么是神經網絡？ * 單層感知機 * 邏輯回歸 * 多層感知機 * 多層感知機分類 * 多層感知機函數近似 # 什么是人工神經網絡？ **人工神經網絡**（**ANN**）是一種信息處理系統，其運行機制受生物神經電路的啟發。 由于它們的特性，神經網絡是機器學習系統（尤其是在人工智能環境中）真正革命的主角。 根據各種架構，人工神經網絡擁有許多相互連接的簡單處理單元。 如果我們看一下稍后報告的 ANN 的架構，可以看到*隱藏單元*在輸入和輸出中與外部層通信，而*輸入*和*輸出單元*僅與網絡的*隱藏層*通信。 每個單元或節點都模擬神經元在生物神經網絡中的作用。 每個節點，即*人工神經元*，都具有非常簡單的操作：如果其接收到的信號總量超過其激活閾值（由所謂的激活函數定義），它將變為活動狀態。 如果節點*變為活動*，它會發射信號，該信號沿著傳輸通道傳輸到與其連接的另一個單元。 每個連接點都充當過濾器，將消息轉換為抑制性信號或興奮性信號，根據其各自的特征來增加或減少強度。 連接點模擬生物突觸，并具有通過將傳輸信號乘以權重（其值取決于連接本身）來權衡傳輸信號強度的基本功能。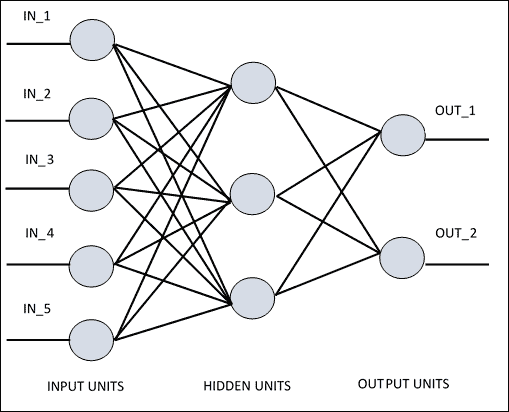  ANN 原理圖 ## 神經網絡架構 連接節點的方式，*總層數*，即輸入和輸出之間的節點級別，以及每層神經元的數量-所有這些都定義了*神經網絡的架構*。 例如，在**多層網絡**中（我們將在本章的第二部分中介紹這些網絡），可以識別層的人工神經元，使得： * 每個神經元都與下一層的所有神經元相連 * 屬于同一層的神經元之間沒有連接 * 層數和每層神經元的數量取決于要解決的問題 現在，我們開始探索神經網絡模型，介紹最簡單的神經網絡模型：單層感知機或所謂的羅森布拉特感知機。 # 單層感知機 單層感知機是第一個神經網絡模型，由 Frank Rosenblatt 于 1958 年提出。 在此模型中，神經元局部記憶的內容由權重向量`W = (w1, w2,......, wn)`組成。 該計算是在計算輸入向量`X =(x1, x2,......, xn)`的總和之后執行的，每個輸入向量均與權重向量的相應元素相乘； 那么輸出中提供的值（即加權總和）將是激活函數的輸入。 如果結果大于某個閾值，則此函數返回`1`，否則返回`-1`。 在下圖中，激活函數是所謂的`sign`函數： ```py +1 x > 0 sign(x)= ?1 otherwise ``` 可以使用其他激活函數，最好是非線性激活函數（例如`sigmoid`函數，我們將在下一部分中看到）。 網絡的學習過程是迭代的：通過使用稱為訓練集的選定集，可以為每個學習周期（稱為周期）稍微修改突觸權重。 在每個循環中，必須修改權重以最小化成本函數，該成本函數特定于所考慮的問題。 最后，當感知機已在訓練集上進行訓練后，將在其他輸入（測試集）上對其進行測試，以驗證其概括能力。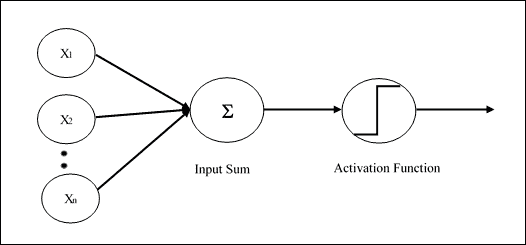  Rosemblatt 的感知機架構 現在讓我們看看如何使用 TensorFlow 對圖像分類問題實現單層神經網絡。 # 邏輯回歸 該算法與我們在第 3 章“機器學習入門”開始看到的規范線性回歸無關，但是它是允許我們解決監督分類問題的算法。 實際上，為了估計因變量，現在我們利用所謂的邏輯函數或 Sigmoid。 正是由于這個函數，我們將此算法稱為邏輯回歸。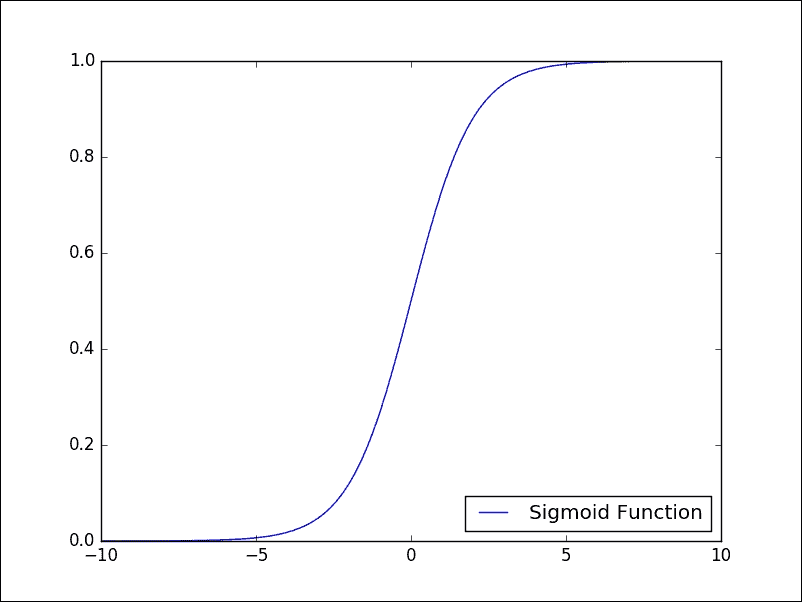 Sigmoid 函數具有以下模式：  Sigmoid 函數 如我們所見，因變量的取值嚴格在`0`和`1`之間，這正是為我們服務的內容。 對于*邏輯回歸*，我們希望我們的函數告訴我們屬于我們的類別某個特定元素的*概率*是多少。 我們再次記得，通過神經網絡對*監督*學習被配置為權重優化的*迭代過程*； 然后根據訓練集的網絡表現對它們進行修改。 實際上，其目標是使*損失函數*最小化，該函數表明網絡行為偏離所需行為的程度。 然后，在*測試集*上驗證網絡的表現，該測試集由除受過訓練的圖像以外的其他圖像組成。 我們將要實現的訓練的基本步驟如下： * 權重在訓練開始時用隨機值初始化。 * 對于訓練集的每個元素，都會計算*誤差*，即期望輸出與實際輸出之間的差。 此誤差用于調整權重。 * 重復該過程，以隨機順序將訓練集的所有示例重新提交給網絡，直到整個訓練集上的誤差不小于某個閾值，或者直到達到最大迭代次數為止。 現在讓我們詳細了解如何使用 TensorFlow 實現邏輯回歸。 我們要解決的問題是對來自 MNIST 數據集的圖像進行分類，如第 3 章，“機器學習入門”中的手寫數字的數據庫。 ## TensorFlow 實現 要實現 TensorFlow，我們需要執行以下步驟： 1. 首先，我們必須導入所有必需的庫： ```py import input_data import tensorflow as tf import matplotlib.pyplot as plt ``` 2. 我們使用第 3 章“機器學習入門”引入的 *MNIST 數據集*部分中的`input_data.read`函數，將圖像上傳到我們的問題中： ```py mnist = input_data.read_data_sets("/tmp/data/", one_hot=True) ``` 3. 然后，我們設置訓練階段的總次數： ```py training_epochs = 25 ``` 4. 我們還必須定義構建模型所需的其他參數： ```py learning_rate = 0.01 batch_size = 100 display_step = 1 ``` 5. 現在我們轉到模型的構建。 ## 建立模型 將`x`定義為輸入張量； 它表示大小為`28 x 28 = 784`像素的 MNIST 數據圖像： ```py x = tf.placeholder("float", [None, 784]) ``` 我們回想起我們的問題是為每種可能的隸屬度類別（從 0 到 9 的數字）分配一個概率值。 在計算的最后，我們將使用概率分布，該分布為我們提供了對我們的預測的置信值。 因此，我們要獲得的輸出將是一個具有`10`概率的輸出張量，每個張量都對應一個數字（當然，概率之和必須為 1）： ```py y = tf.placeholder("float", [None, 10]) ``` 為了給每個圖像分配概率，我們將使用所謂的 softmax 激活函數。 `softmax`函數在兩個主要步驟中指定： * 計算*證據*，即某個圖像屬于特定類別 * 將證據轉換為屬于 10 個可能類別中的每個類別的*概率* 為了求值證據，我們首先將權重輸入張量定義為`W`： ```py W = tf.Variable(tf.zeros([784, 10])) ``` 對于給定的圖像，我們可以通過簡單地將張量`W`與輸入張量`x`相乘來求值每個類別`i`的證據。 使用 TensorFlow，我們應該具有以下內容： ```py evidence = tf.matmul(x, W) ``` 通常，模型包括代表偏差的額外參數，該參數表示一定程度的不確定性。 在我們的案例中，證據的最終公式如下： ```py evidence = tf.matmul(x, W) + b ``` 這意味著，對于每個`i`（從 0 到 9），我們都有一個`Wi`矩陣元素`784 (28 × 28)`，其中矩陣的每個元素`j`與輸入圖像的相應分量`j`相乘（784 部分），并添加相應的偏置元素`bi`。 因此，要定義證據，我們必須定義以下偏差張量： ```py b = tf.Variable(tf.zeros([10])) ``` 第二步是最終使用`softmax`函數獲得概率的輸出向量，即`activation`： ```py activation = tf.nn.softmax(tf.matmul(x, W) + b) ``` TensorFlow 的`tf.nn.softmax`函數提供了來自輸入證據張量的基于概率的輸出。 一旦實現模型，我們就可以指定必要的代碼，以通過迭代訓練算法找到權重`W`和偏置`b`網絡。 在每次迭代中，訓練算法都會獲取訓練數據，應用神經網絡，并將結果與??預期結果進行比較。 ### 注意 TensorFlow 提供了許多其他激活函數。 有關更好的參考，請參見[這里](https://www.tensorflow.org/versions/r0.8/api_docs/index.html)。 為了訓練我們的模型并知道何時有一個好的模型，我們必須定義如何定義模型的準確率。 我們的目標是嘗試獲取參數`W`和`b`的值，這些值會最小化指示模型有多糟糕的度量值。 不同的度量標準計算了期望輸出和訓練數據輸出之間的誤差。 常見的誤差度量是均方誤差或*平方歐幾里德距離*。 但是，有一些研究發現建議對這種神經網絡使用其他指標。 在此示例中，我們使用所謂的`cross-entropy error`函數。 它定義為： ```py cross_entropy = y*tf.lg(activation) ``` 為了最小化`cross_entropy`，我們可以使用`tf.reduce_mean`和`tf.reduce_sum`的以下組合來構建成本函數： ```py cost = tf.reduce_mean\ (-tf.reduce_sum\ (cross_entropy, reduction_indices=1)) ``` 然后，我們必須使用梯度下降優化算法將其最小化： ```py optimizer = tf.train.GradientDescentOptimizer\ (learning_rate).minimize(cost) ``` 只需幾行代碼即可構建神經網絡模型！ ## 啟動會話 現在是構建會話并啟動我們的神經網絡模型的時候了。 我們修復了以下列表以可視化訓練過程： ```py avg_set = [] epoch_set=[] ``` 然后我們初始化 TensorFlow 變量： ```py init = tf.initialize_all_variables() ``` 開始會話： ```py with tf.Session() as sess: sess.run(init) ``` 如前所述，每個周期都是一個訓練周期： ```py for epoch in range(training_epochs): avg_cost = 0. total_batch = int(mnist.train.num_examples/batch_size) ``` 然后我們遍歷所有批次： ```py for i in range(total_batch): batch_xs, batch_ys = \ mnist.train.next_batch(batch_size) ``` 使用批量數據擬合訓練： ```py sess.run(optimizer, feed_dict={x: batch_xs, y: batch_ys}) ``` 用給定的圖像值（`x`）和實際輸出（`y_`）計算運行`train_step`函數的平均損失： ```py avg_cost += sess.run\ (cost, feed_dict={x: batch_xs,\ y: batch_ys})/total_batch ``` 在計算過程中，我們每個周期顯示一個日志： ```py if epoch % display_step == 0: print "Epoch:",\ '%04d' % (epoch+1),\ "cost=","{:.9f}".format(avg_cost) print " Training phase finished" ``` 讓我們獲得模式的準確率。 如果`y`值最高的索引與實數向量中的`correct_prediction`均值使我們具有準確率，則是正確的。 我們需要使用測試集（`mnist.test`）運行準確率函數。 我們使用`x`和`y`的關鍵圖像和標簽： ```py correct_prediction = tf.equal\ (tf.argmax(activation, 1),\ tf.argmax(y, 1)) accuracy = tf.reduce_mean\ (tf.cast(correct_prediction, "float")) print "MODEL accuracy:", accuracy.eval({x: mnist.test.images,\ y: mnist.test.labels}) ``` ## 測試和評估 我們之前顯示了訓練階段，并且對于每個周期，我們都打印了相對成本函數： ```py Python 2.7.10 (default, Oct 14 2015, 16:09:02) [GCC 5.2.1 20151010] on linux2 Type "copyright", "credits" or "license()" for more information. >>> ======================= RESTART ============================ >>> Extracting /tmp/data/train-images-idx3-ubyte.gz Extracting /tmp/data/train-labels-idx1-ubyte.gz Extracting /tmp/data/t10k-images-idx3-ubyte.gz Extracting /tmp/data/t10k-labels-idx1-ubyte.gz Epoch: 0001 cost= 1.174406662 Epoch: 0002 cost= 0.661956009 Epoch: 0003 cost= 0.550468774 Epoch: 0004 cost= 0.496588717 Epoch: 0005 cost= 0.463674555 Epoch: 0006 cost= 0.440907706 Epoch: 0007 cost= 0.423837747 Epoch: 0008 cost= 0.410590841 Epoch: 0009 cost= 0.399881751 Epoch: 0010 cost= 0.390916621 Epoch: 0011 cost= 0.383320325 Epoch: 0012 cost= 0.376767031 Epoch: 0013 cost= 0.371007620 Epoch: 0014 cost= 0.365922904 Epoch: 0015 cost= 0.361327561 Epoch: 0016 cost= 0.357258660 Epoch: 0017 cost= 0.353508228 Epoch: 0018 cost= 0.350164634 Epoch: 0019 cost= 0.347015593 Epoch: 0020 cost= 0.344140861 Epoch: 0021 cost= 0.341420144 Epoch: 0022 cost= 0.338980592 Epoch: 0023 cost= 0.336655581 Epoch: 0024 cost= 0.334488012 Epoch: 0025 cost= 0.332488823 Training phase finished ``` 如您所見，在訓練階段，成本函數被最小化。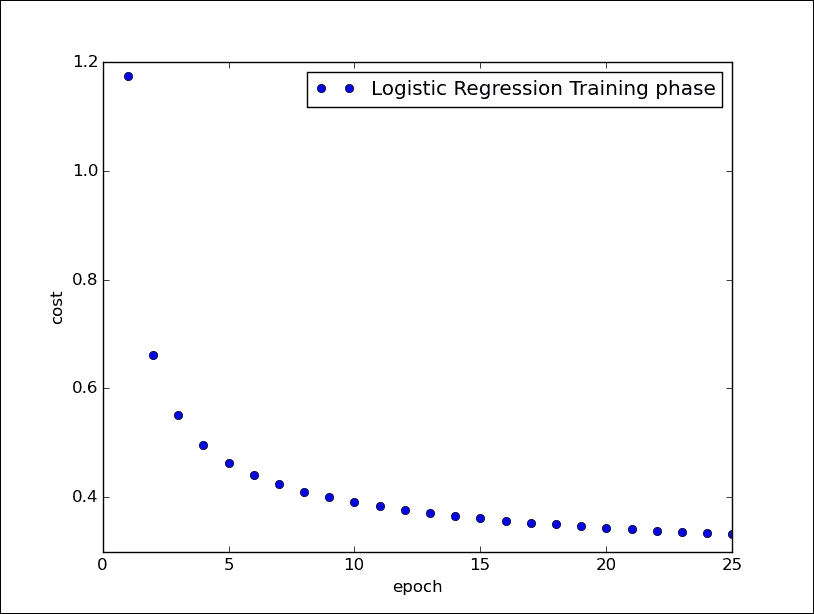 在測試的最后，我們展示了實現模型的準確率： ```py Model Accuracy: 0.9475 >>> ``` 最后，使用以下代碼行，我們可以可視化網絡的訓練階段： ```py plt.plot(epoch_set,avg_set, 'o',\ label='Logistic Regression Training phase') plt.ylabel('cost') plt.xlabel('epoch') plt.legend() plt.show() ```  邏輯回歸訓練階段 ## 源代碼 ```py # Import MINST data import input_data mnist = input_data.read_data_sets("/tmp/data/", one_hot=True) import tensorflow as tf import matplotlib.pyplot as plt # Parameters learning_rate = 0.01 training_epochs = 25 batch_size = 100 display_step = 1 # tf Graph Input x = tf.placeholder("float", [None, 784]) y = tf.placeholder("float", [None, 10]) # Create model # Set model weights W = tf.Variable(tf.zeros([784, 10])) b = tf.Variable(tf.zeros([10])) # Construct model activation = tf.nn.softmax(tf.matmul(x, W) + b) # Minimize error using cross entropy cross_entropy = y*tf.log(activation) cost = tf.reduce_mean\ (-tf.reduce_sum\ (cross_entropy,reduction_indices=1)) optimizer = tf.train.\ GradientDescentOptimizer(learning_rate).minimize(cost) #Plot settings avg_set = [] epoch_set=[] # Initializing the variables init = tf.initialize_all_variables() # Launch the graph with tf.Session() as sess: sess.run(init) # Training cycle for epoch in range(training_epochs): avg_cost = 0. total_batch = int(mnist.train.num_examples/batch_size) # Loop over all batches for i in range(total_batch): batch_xs, batch_ys = \ mnist.train.next_batch(batch_size) # Fit training using batch data sess.run(optimizer, \ feed_dict={x: batch_xs, y: batch_ys}) # Compute average loss avg_cost += sess.run(cost,feed_dict=\ {x: batch_xs,\ y: batch_ys})/total_batch # Display logs per epoch step if epoch % display_step == 0: print "Epoch:", '%04d' % (epoch+1),\ "cost=", "{:.9f}".format(avg_cost) avg_set.append(avg_cost) epoch_set.append(epoch+1) print "Training phase finished" plt.plot(epoch_set,avg_set, 'o',\ label='Logistic Regression Training phase') plt.ylabel('cost') plt.xlabel('epoch') plt.legend() plt.show() # Test model correct_prediction = tf.equal\ (tf.argmax(activation, 1),\ tf.argmax(y, 1)) # Calculate accuracy accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print "Model accuracy:", accuracy.eval({x: mnist.test.images,\ y: mnist.test.labels}) ``` # 多層感知機 更復雜和有效的架構是**多層感知機**（**MLP**）。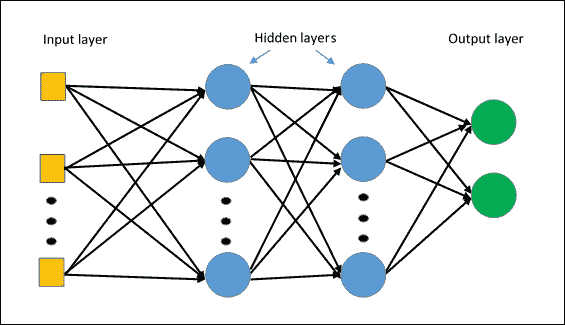 它基本上由多層感知機組成，因此至少存在*隱藏的層*，即**未連接到網絡的輸入或輸出**：  MLP 架構 根據上一段中概述的原則，通常使用監督學習來訓練這種類型的網絡。 特別地，用于 MLP 網絡的典型學習算法是所謂的反向傳播算法。 ### 注意 反向傳播算法是一種用于神經網絡的學習算法。 它將系統的輸出值與所需值進行比較。 基于由此計算出的差異（即誤差），該算法通過逐步收斂所需輸出值的集合來修改神經網絡的突觸權重。 重要的是要注意，在 MLP 網絡中，盡管您不知道網絡隱藏層的神經元的期望輸出，但是始終可以通過基于最小誤差函數的最小化應用有監督的學習方法。 梯度下降技術的應用。 在以下示例中，我們顯示了針對圖像分類問題（MNIST）的 MLP 實現。 ## 多層感知機分類 導入必要的庫： ```py import input_data import tensorflow as tf import matplotlib.pyplot as plt ``` 加載圖像進行分類： ```py mnist = input_data.read_data_sets("/tmp/data/", one_hot=True) ``` 修復 MLP 模型的一些參數： 網絡學習率： ```py learning_rate = 0.001 ``` 周期： ```py training_epochs = 20 ``` 要分類的圖像數量： ```py batch_size = 100 display_step = 1 ``` 第一層的神經元數量： ```py n_hidden_1 = 256 ``` 第二層的神經元數量： ```py n_hidden_2 = 256 ``` 輸入的大小（每個圖像都有`784`像素）： ```py n_input = 784 # MNIST data input (img shape: 28*28) ``` 輸出類的大小： ```py n_classes = 10 ``` 因此，應該注意的是，盡管對于給定的應用，輸入和輸出大小是完美定義的，但是對于如何定義隱藏層的數量和每層神經元的數量，沒有嚴格的標準。 每個選擇都必須基于類似應用的經驗，例如： * 當增加隱藏層的數量時，我們還應該在學習階段增加必要的訓練集的大小，并增加要更新的連接數。 這導致訓練時間*增加*。 * 另外，如果隱藏層中的神經元太多，不僅有更多的權重需要更新，而且網絡還傾向于從訓練示例集中學習太多，從而導致*泛化能力很差*。 但是，如果隱藏的神經元太少，即使使用訓練集，網絡*也無法學習*。 ### 建立模型 輸入層是`x`張量`[1×784]`，它表示要分類的圖像： ```py x = tf.placeholder("float", [None, n_input]) ``` 輸出張量`y`等于類數： ```py y = tf.placeholder("float", [None, n_classes]) ``` 在中間，我們有兩個隱藏層。 第一層由權重的`h`張量構成，其權重為`[784 × 256]`，其中`256`是該層的節點總數： ```py h = tf.Variable(tf.random_normal([n_input, n_hidden_1])) ``` 對于第 1 層，我們必須定義各自的偏置張量： ```py bias_layer_1 = tf.Variable(tf.random_normal([n_hidden_1])) ``` 每個神經元接收要與`hij`權重連接相結合進行分類的輸入圖像像素，并添加到偏置張量的各個值中： ```py layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x,h),bias_layer_1)) ``` 它通過`activation`函數將其輸出發送到下一層的神經元。 必須說，每個神經元的特征可能不同，但是在實踐中，我們對所有神經元（通常為 Sigmoid）采用一個共同的特征。 有時輸出神經元具有線性激活函數。 有趣的是，隱藏層中神經元的激活函數不能是線性的，因為在這種情況下，MLP 網絡將等效于具有兩層的網絡，因此不再是 MLP 類型。 第二層必須執行與第一相同的步驟。 第二中間層由權重張量`[256 × 256]`的形狀表示： ```py w = tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2])) ``` 有偏置張量： ```py bias_layer_2 = tf.Variable(tf.random_normal([n_hidden_2])) ``` 第二層中的每個神經元都接收來自第 1 層神經元的輸入，并與權重`Wij`連接相結合，并添加到第 2 層的各個偏差中： ```py layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1,w),bias_layer_2)) ``` 它將其輸出發送到下一層，即輸出層： ```py output = tf.Variable(tf.random_normal([n_hidden_2, n_classes])) bias_output = tf.Variable(tf.random_normal([n_classes])) output_layer = tf.matmul(layer_2, output) + bias_output ``` 輸出層接收來自層 2 的 n 個刺激（256）作為輸入，該 n 個刺激被轉換為每個數的相應概率類別。 至于邏輯回歸，我們然后定義`cost`函數： ```py cost = tf.reduce_mean\ (tf.nn.softmax_cross_entropy_with_logits\ (output_layer, y)) ``` TensorFlow 函數`tf` `.nn.softmax_cross_entropy_with_logits`計算 softmax 層的成本。 僅在訓練期間使用。 logits 是模型輸出的未歸一化對數概率（將 softmax 歸一化之前輸出的值）。 使`cost`函數最小化的相應優化器是： ```py optimizer = tf.train.AdamOptimizer\ (learning_rate=learning_rate).minimize(cost) ``` `tf.train.AdamOptimizer`使用 Kingma 和 Ba 的 Adam 算法控制學習率。 與簡單的`tf.train.GradientDescentOptimizer`相比，Adam 具有多個優點。 實際上，它使用了較大的有效步長，并且該算法將收斂到該步長而無需微調。 一個簡單的`tf.train.GradientDescentOptimizer`也可以在您的 MLP 中使用，但需要更多的超參數調整，才能使其快速收斂。 ### 注意 TensorFlow 提供了優化器基類來計算損失的梯度并將梯度應用于變量。 此類定義用于添加操作以訓練模型的 API。 您永遠不會直接使用此類，而是實例化其子類之一。 請參閱[這里](https://www.tensorflow.org/versions/r0.8/api_docs/python/train.html#Optimizer)以查看優化程序的實現。 ### 啟動會話 以下是啟動會話的步驟： 1. 定義集合： ```py avg_set = [] epoch_set=[] ``` 2. 初始化變量： ```py init = tf.initialize_all_variables() ``` 3. 啟動圖： ```py with tf.Session() as sess: sess.run(init) ``` 4. 定義訓練周期： ```py for epoch in range(training_epochs): avg_cost = 0. total_batch = int(mnist.train.num_examples/batch_size) ``` 5. 循環所有批次（100）： ```py for i in range(total_batch): batch_xs, batch_ys = mnist.train.next_batch(batch_size) ``` 6. 使用批次數據進行擬合訓練： ```py sess.run(optimizer, feed_dict={x: batch_xs, y: batch_ys}) ``` 7. 計算平均損失： ```py avg_cost += sess.run(cost,feed_dict={x: batch_xs,\ y: batch_ys})/total_batch Display logs per epoch step if epoch % display_step == 0: print "Epoch:", '%04d' % (epoch+1),\ "cost=", "{:.9f}".format(avg_cost) avg_set.append(avg_cost) epoch_set.append(epoch+1) print "Training phase finished" ``` 8. 使用以下代碼行，我們繪制了訓練階段： ```py plt.plot(epoch_set,avg_set, 'o', label='MLP Training phase') plt.ylabel('cost') plt.xlabel('epoch') plt.legend() plt.show() ``` 9. 最后，我們可以測試 MLP 模型： ```py correct_prediction = tf.equal(tf.argmax(output_layer, 1),\ tf.argmax(y, 1)) evaluating its accuracy accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print "Model Accuracy:", accuracy.eval({x: mnist.test.images,\ y: mnist.test.labels}) ``` 10. 這是 20 個周期后的輸出結果： ```py Python 2.7.10 (default, Oct 14 2015, 16:09:02) [GCC 5.2.1 20151010] on linux2 Type "copyright", "credits" or "license()" for more information. >>> ========================== RESTART ============================== >>> Succesfully downloaded train-images-idx3-ubyte.gz 9912422 bytes. Extracting /tmp/data/train-images-idx3-ubyte.gz Succesfully downloaded train-labels-idx1-ubyte.gz 28881 bytes. Extracting /tmp/data/train-labels-idx1-ubyte.gz Succesfully downloaded t10k-images-idx3-ubyte.gz 1648877 bytes. Extracting /tmp/data/t10k-images-idx3-ubyte.gz Succesfully downloaded t10k-labels-idx1-ubyte.gz 4542 bytes. Extracting /tmp/data/t10k-labels-idx1-ubyte.gz Epoch: 0001 cost= 1.723947845 Epoch: 0002 cost= 0.539266024 Epoch: 0003 cost= 0.362600502 Epoch: 0004 cost= 0.266637279 Epoch: 0005 cost= 0.205345784 Epoch: 0006 cost= 0.159139332 Epoch: 0007 cost= 0.125232637 Epoch: 0008 cost= 0.098572041 Epoch: 0009 cost= 0.077509963 Epoch: 0010 cost= 0.061127526 Epoch: 0011 cost= 0.048033808 Epoch: 0012 cost= 0.037297983 Epoch: 0013 cost= 0.028884999 Epoch: 0014 cost= 0.022818390 Epoch: 0015 cost= 0.017447586 Epoch: 0016 cost= 0.013652348 Epoch: 0017 cost= 0.010417282 Epoch: 0018 cost= 0.008079228 Epoch: 0019 cost= 0.006203546 Epoch: 0020 cost= 0.004961207 Training phase finished Model Accuracy: 0.9775 >>> ``` 我們在下圖中顯示了訓練階段：  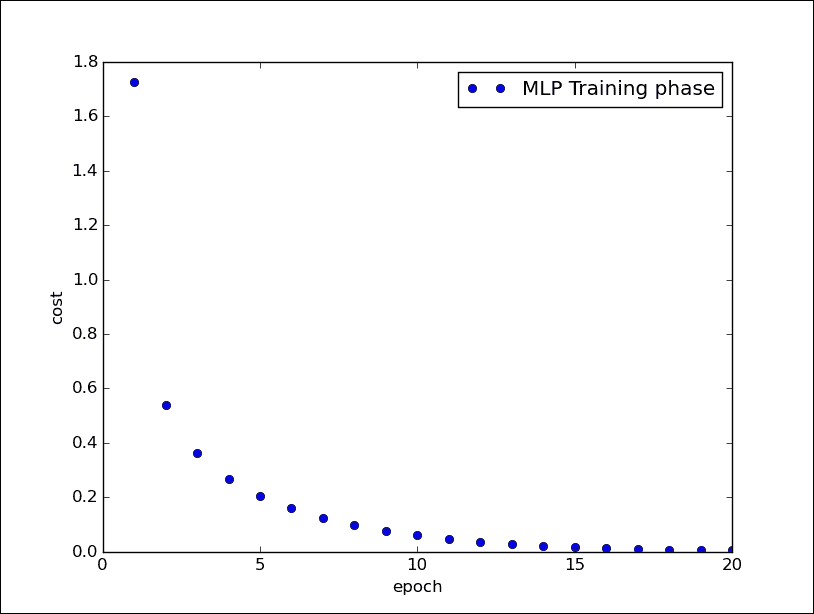多層感知機的訓練階段 ### 源代碼 ```py # Import MINST data import input_data mnist = input_data.read_data_sets("/tmp/data/", one_hot=True) import tensorflow as tf import matplotlib.pyplot as plt # Parameters learning_rate = 0.001 training_epochs = 20 batch_size = 100 display_step = 1 # Network Parameters n_hidden_1 = 256 # 1st layer num features n_hidden_2 = 256 # 2nd layer num features n_input = 784 # MNIST data input (img shape: 28*28) n_classes = 10 # MNIST total classes (0-9 digits) # tf Graph input x = tf.placeholder("float", [None, n_input]) y = tf.placeholder("float", [None, n_classes]) #weights layer 1 h = tf.Variable(tf.random_normal([n_input, n_hidden_1])) #bias layer 1 bias_layer_1 = tf.Variable(tf.random_normal([n_hidden_1])) #layer 1 layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x,h),bias_layer_1)) #weights layer 2 w = tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2])) #bias layer 2 bias_layer_2 = tf.Variable(tf.random_normal([n_hidden_2])) #layer 2 layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1,w),bias_layer_2)) #weights output layer output = tf.Variable(tf.random_normal([n_hidden_2, n_classes])) #biar output layer bias_output = tf.Variable(tf.random_normal([n_classes])) #output layer output_layer = tf.matmul(layer_2, output) + bias_output # cost function cost = tf.reduce_mean\ (tf.nn.softmax_cross_entropy_with_logits(output_layer, y)) # optimizer optimizer = tf.train.AdamOptimizer\ (learning_rate=learning_rate).minimize(cost) #Plot settings avg_set = [] epoch_set=[] # Initializing the variables init = tf.initialize_all_variables() # Launch the graph with tf.Session() as sess: sess.run(init) # Training cycle for epoch in range(training_epochs): avg_cost = 0. total_batch = int(mnist.train.num_examples/batch_size) # Loop over all batches for i in range(total_batch): batch_xs, batch_ys = mnist.train.next_batch(batch_size) # Fit training using batch data sess.run(optimizer, feed_dict={x: batch_xs, y: batch_ys}) # Compute average loss avg_cost += sess.run(cost, \ feed_dict={x: batch_xs,\ y: batch_ys})/total_batch # Display logs per epoch step if epoch % display_step == 0: print "Epoch:", '%04d' % (epoch+1),\ "cost=", "{:.9f}".format(avg_cost) avg_set.append(avg_cost) epoch_set.append(epoch+1) print "Training phase finished" plt.plot(epoch_set,avg_set, 'o', label='MLP Training phase') plt.ylabel('cost') plt.xlabel('epoch') plt.legend() plt.show() # Test model correct_prediction = tf.equal(tf.argmax(output_layer, 1),\ tf.argmax(y, 1)) # Calculate accuracy accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print "Model Accuracy:", accuracy.eval({x: mnist.test.images,\ y: mnist.test.labels}) ``` ## 多層感知機函數近似 在以下示例中，我們實現了一個 MLP 網絡，該網絡將能夠學習任意函數`f (x)`的趨勢。 在訓練階段，網絡將必須從一組已知點中學習`x`和`f (x)`，而在測試階段，網絡將僅從`x`值中扣除`f (x)`的值。 這個非常簡單的網絡將由單個隱藏層構建。 導入必要的庫： ```py import tensorflow as tf import numpy as np import math, random import matplotlib.pyplot as plt ``` 我們建立數據模型。 要學習的函數將遵循`cosine`函數的趨勢，并針對`1000`點進行了評估，并向其中添加了很少的隨機誤差（噪聲）以重現真實情況： ```py NUM_points = 1000 np.random.seed(NUM_points) function_to_learn = lambda x: np.cos(x) + \ 0.1*np.random.randn(*x.shape) ``` 我們的 MLP 網絡將由`10`神經元的隱藏層形成： ```py layer_1_neurons = 10 ``` 網絡一次學習`100`點，總共學習`1500`個學習周期（周期）： ```py batch_size = 100 NUM_EPOCHS = 1500 ``` 最后，我們構造訓練集和測試集： ```py all_x contiene tutti i punti all_x = np.float32(np.random.uniform\ (-2*math.pi, 2*math.pi,\ (1, NUM_points))).T np.random.shuffle(all_x) train_size = int(900) ``` 前`900`點在訓練集中： ```py x_training = all_x[:train_size] y_training = function_to_learn(x_training) ``` 最后一個`100`將在驗證集中： ```py x_validation = all_x[train_size:] y_validation = function_to_learn(x_validation) ``` 使用 matplotlib，我們顯示以下集合： ```py plt.figure(1) plt.scatter(x_training, y_training, c='blue', label='train') plt.scatter(x_validation, y_validation,c='red',label='validation') plt.legend() plt.show() ```  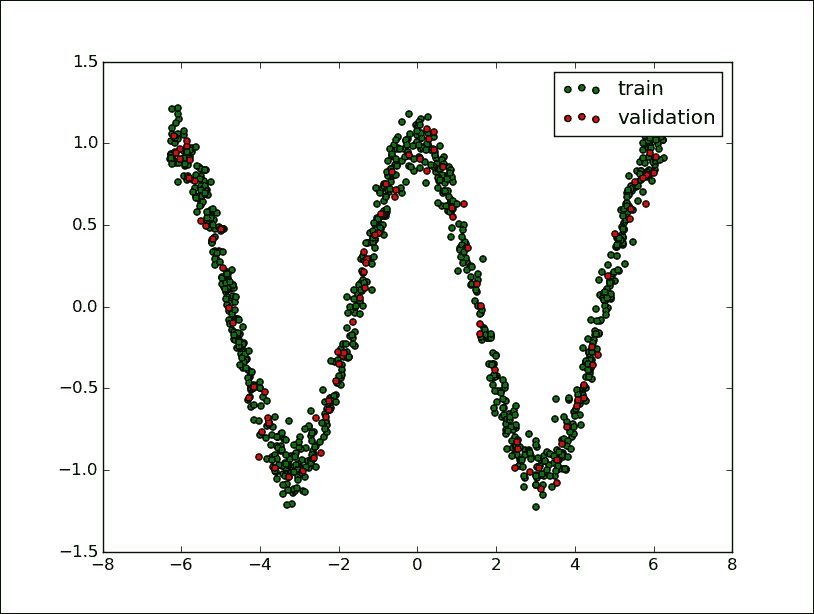訓練和驗證集 ### 建立模型 首先，我們為輸入張量（`X`）和輸出張量（`Y`）創建占位符： ```py X = tf.placeholder(tf.float32, [None, 1], name="X") Y = tf.placeholder(tf.float32, [None, 1], name="Y") ``` 然后，我們構建`[1 x 10]`尺寸的隱藏層： ```py w_h = tf.Variable(tf.random_uniform([1, layer_1_neurons],\ minval=-1, maxval=1, \ dtype=tf.float32)) b_h = tf.Variable(tf.zeros([1, layer_1_neurons], \ dtype=tf.float32)) ``` 它從`X`輸入張量接收輸入值，并與權重`w_hij`連接相結合，并加上第 1 層的各個偏置： ```py h = tf.nn.sigmoid(tf.matmul(X, w_h) + b_h) ``` 輸出層是一個`[10 x 1]`張量： ```py w_o = tf.Variable(tf.random_uniform([layer_1_neurons, 1],\ minval=-1, maxval=1,\ dtype=tf.float32)) b_o = tf.Variable(tf.zeros([1, 1], dtype=tf.float32)) ``` 第二層中的每個神經元都從層 1 的神經元接收輸入，并與權重`w_oij`連接相結合，并與輸出層的各個偏置相加： ```py model = tf.matmul(h, w_o) + b_o ``` 然后，我們為新定義的模型定義優化器： ```py train_op = tf.train.AdamOptimizer().minimize\ (tf.nn.l2_loss(model - Y)) ``` 我們還注意到，在這種情況下，采用的成本函數如下： ```py tf.nn.l2_loss(model - Y) ``` `tf.nn.l2_loss`函數是一個 TensorFlow，它計算不具有`sqrt`的張量的 L2 范數的一半，也就是說，前一個函數的輸出如下： ```py output = sum((model - Y) ** 2) / 2 ``` 對于我們的示例，`tf.nn.l2_loss`函數可以是可行的成本函數。 ### 啟動會話 讓我們建立求值圖： ```py sess = tf.Session() sess.run(tf.initialize_all_variables()) ``` 現在我們可以啟動學習過程： ```py errors = [] for i in range(NUM_EPOCHS): for start, end in zip(range(0, len(x_training), batch_size),\ range(batch_size,\ len(x_training), batch_size)): sess.run(train_op, feed_dict={X: x_training[start:end],\ Y: y_training[start:end]}) cost = sess.run(tf.nn.l2_loss(model - y_validation),\ feed_dict={X:x_validation}) errors.append(cost) if i%100 == 0: print "epoch %d, cost = %g" % (i, cost) ``` 將這個網絡運行 1400 個周期，我們將看到誤差逐漸減少并最終收斂： ```py Python 2.7.10 (default, Oct 14 2015, 16:09:02) [GCC 5.2.1 20151010] on linux2 Type "copyright", "credits" or "license()" for more information. >>> ======================= RESTART ============================ >>> epoch 0, cost = 55.9286 epoch 100, cost = 22.0084 epoch 200, cost = 18.033 epoch 300, cost = 14.0481 epoch 400, cost = 9.74721 epoch 500, cost = 5.83419 epoch 600, cost = 3.05434 epoch 700, cost = 1.53706 epoch 800, cost = 0.91719 epoch 900, cost = 0.726675 epoch 1000, cost = 0.668316 epoch 1100, cost = 0.633737 epoch 1200, cost = 0.608306 epoch 1300, cost = 0.590429 epoch 1400, cost = 0.574602 >>> ``` **以下代碼行使我們能夠顯示成本在運行周期中的變化： ```py plt.plot(errors,label='MLP Function Approximation') plt.xlabel('epochs') plt.ylabel('cost') plt.legend() plt.show() ```  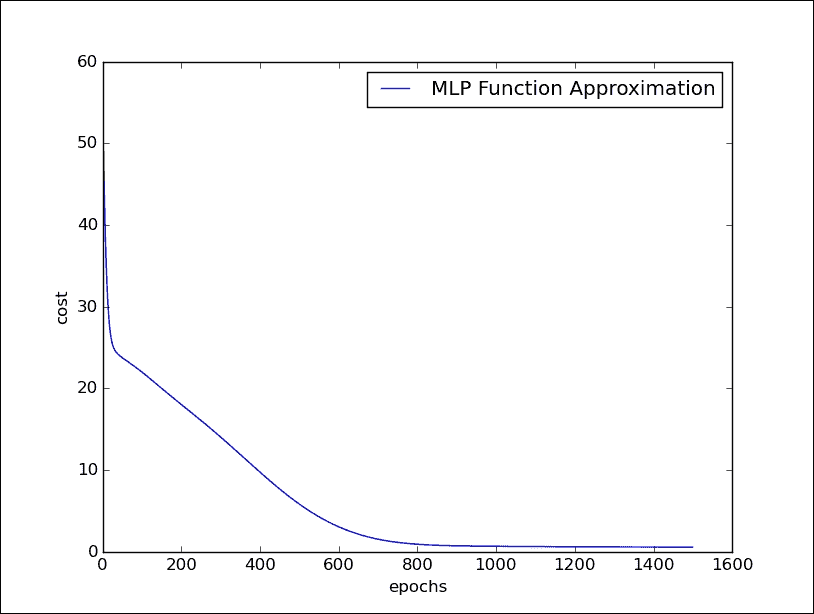多層感知機的訓練階段 # 總結 在本章中，我們介紹了*人工神經網絡*。 人工神經元是一種數學模型，在某種程度上模仿了活神經元的特性。 網絡的每個神經元都有一個非常簡單的操作，包括接收到的信號總量超過激活閾值時變為活動狀態。 學習過程通常是*監督的*：神經網絡使用訓練集來推斷輸入和相應輸出之間的關系，而學習算法會修改網絡的權重以使成本函數*最小化*，它表示*訓練集*有關的*預測誤差*。 如果訓練成功，則即使事先不知道輸出結果，神經網絡也將能夠做出預測。 在本章中，我們使用 TensorFlow 實現了一些涉及神經網絡的示例。 在使用 *Rosemblatt 的感知機*進行分類的問題中，我們已經看到神經網絡作為*邏輯回歸*算法來解決分類和回歸問題。 在本章的最后，在實現*圖像分類器*之前，我們介紹了*多層感知機*架構，然后在*數學函數仿真器*的實現中，我們已經看到了該架構的實際應用。 在下一章中，我們最后介紹深度學習模型； 我們將研究和實現更復雜的神經網絡架構，例如卷積神經網絡和循環神經網絡。