# 二、使用深度學習解決回歸問題 在本章中，我們將構建一個簡單的**多層感知器**（**MLP**），它是具有單個隱藏層的神經網絡的奇特名稱，用于解決回歸問題。 然后，我們將深入研究具有多個隱藏層的深度神經網絡。 在此過程中，我們將探索模型的表現和過擬合。 所以，讓我們開始吧！ 我們將在本章介紹以下主題： * 回歸分析和深度神經網絡 * 將深度神經網絡用于回歸 * 在 Keras 中建立 MLP * 在 Keras 中建立深度神經網絡 * 保存和加載經過訓練的 Keras 模型 # 回歸分析和深度神經網絡 在經典回歸分析中，我們使用線性模型來學習一組獨立變量和因變量之間的關系。 在找到這種關系時，我們希望能夠在給定自變量值的情況下預測因變量的值。 進行回歸分析的第二個重要原因是要了解當所有其他自變量保持恒定時單個自變量對因變量的影響。 傳統多元線性回歸的一大優點是線性模型的*其他條件不變*屬性。 我們可以通過使用與該自變量關聯的學習權重來解釋單個自變量對因變量的影響，而無需考慮其他自變量。 這種解釋充其量是具有挑戰性的，需要我們對我們的數據和模型做出很多假設。 但是，它通常非常有用。 深度神經網絡很難解釋，盡管嘗試這樣做是一個活躍的研究領域。 有關介紹深度神經網絡的當前狀態的介紹，請查看 Montavon 等人的[《解釋和理解深度神經網絡的方法》](https://arxiv.org/abs/1706.07979)。 # 將神經網絡用于回歸的好處 在本章的其余部分，我們將重點介紹使用深度神經網絡進行預測。 與使用傳統的多元線性回歸進行比較時，您會很高興地發現我們的神經網絡具有以下優勢： * 我們不需要選擇或篩選特征。 神經網絡是功能強大的特征工程機器，可以了解哪些特征是相關的，而忽略了無關的特征。 * 給定足夠復雜的網絡，還可以學習特征交互（例如，除了`x[1]`和`x[2]`的獨立效應，`x[1] * x[2]`的效應）） * 您可能現在已經猜到了，我們還可以學習更高階的多項式關系（例如`x[2]^3`） * 最后，只要我們確保最終激活可以對分布進行建模，我們就不必只對正態分布建模或對非正態分布使用不同的模型。 # 將神經網絡用于回歸時要考慮的缺點 但這并不是所有的彩虹和小貓，使用神經網絡解決這些真正簡單的問題也有一些弊端。 最明顯的缺點是： * 如前所述，神經網絡不容易解釋。 * 當具有許多特征和大量數據時，神經網絡最有效。 許多簡單的回歸問題還不夠大，無法真正從神經網絡中受益。 * 在很多情況下，傳統的多元回歸或樹模型（例如梯度提升樹）在此類問題上的表現將優于神經網絡。 越復雜，就越適合神經網絡。 # 將深度神經網絡用于回歸 既然您已經希望了解為什么（不希望）使用深度神經網絡進行回歸，那么我將向您展示如何做到這一點。 雖然它不像在 **scikit-learn** 中使用**線性回歸器**那樣簡單，但我認為使用 **Keras** 會很容易。 最重要的是，Keras 將允許您快速迭代模型架構而無需更改大量代碼。 # 如何規劃機器學習問題 在構建新的神經網絡時，我建議每次都遵循相同的基本步驟。 深度神經網絡很快就會變得非常復雜。 進行一點計劃和組織，大大加快您的工作流程！ 以下是構建深度神經網絡的步驟： 1. 概述您要解決的問題。 2. 確定模型的輸入和輸出。 3. 選擇`cost`函數和指標。 4. 創建一個初始的網絡架構。 5. 訓練和調整網絡。 # 定義示例問題 在我們的示例問題中，我們將使用 P. Cortez 等人創建的[葡萄酒質量數據集](https://archive.ics.uci.edu/ml/datasets/wine+quality)。 考慮到白酒的其他 10 個化學特性，我們將預測白葡萄酒數據中所含酒精的百分比。 此數據集中總共有 4,898 個觀測值或元素，對于經典回歸問題而言可能很大，但對于深度學習問題而言卻很小。 一些快速的探索性數據分析將告訴我們，我們將用來預測酒精含量的 10 個化學特征在不同尺度上都是連續變量。 # 加載數據集 雖然可能不是機器學習問題中最有趣的部分，但加載數據是重要的一步。 我將在這里介紹我的數據加載方法，以便您可以了解如何處理數據集。 ```py from sklearn.preprocessing import StandardScaler import pandas as pd TRAIN_DATA = "./data/train/train_data.csv" VAL_DATA = "./data/val/val_data.csv" TEST_DATA = "./data/test/test_data.csv" def load_data(): """Loads train, val, and test datasets from disk""" train = pd.read_csv(TRAIN_DATA) val = pd.read_csv(VAL_DATA) test = pd.read_csv(TEST_DATA) # we will use sklearn's StandardScaler to scale our data to 0 mean, unit variance. scaler = StandardScaler() train = scaler.fit_transform(train) val = scaler.transform(val) test = scaler.transform(test) # we will use a dict to keep all this data tidy. data = dict() data["train_y"] = train[:, 10] data["train_X"] = train[:, 0:9] data["val_y"] = val[:, 10] data["val_X"] = val[:, 0:9] data["test_y"] = test[:, 10] data["test_X"] = test[:, 0:9] # it's a good idea to keep the scaler (or at least the mean/variance) so we can unscale predictions data["scaler"] = scaler return data ``` 當我從 csv，excel 甚至是 DBMS 中讀取數據時，第一步通常是將其加載到 pandas 數據框中。 標準化我們的數據很重要，這樣每個特征都應具有可比的范圍，并且所有這些范圍都應位于激活函數的范圍之內。 在這里，我使用了 Scikit-Learn 的`StandardScaler`完成此任務。 這為我們提供了一個形狀完整的數據集`(4898, 10)`。 我們的目標變量`alcohol`的百分比介于 8% 和 14.2% 之間。 在加載數據之前，我已經對數據進行了隨機采樣并將其劃分為`train`，`val`和`test`數據集，因此我們在這里不必擔心。 最后，`load_data()`函數返回一個字典，該字典將所有內容保持整齊并放在一個位置。 如果您以后看到我參考數據`[X_train]`，則知道我正在參考訓練數據集，該數據集已存儲在數據字典中。 。 [該項目的代碼和數據均可在該書的 GitHub 網站上找到](https://github.com/mbernico/deep_learning_quick_reference)。 # 定義成本函數 對于回歸任務，最常見的成本函數是**均方根誤差**（**RMSE**）和**平均絕對誤差**（**MAE**）。 我將在這里使用 MAE。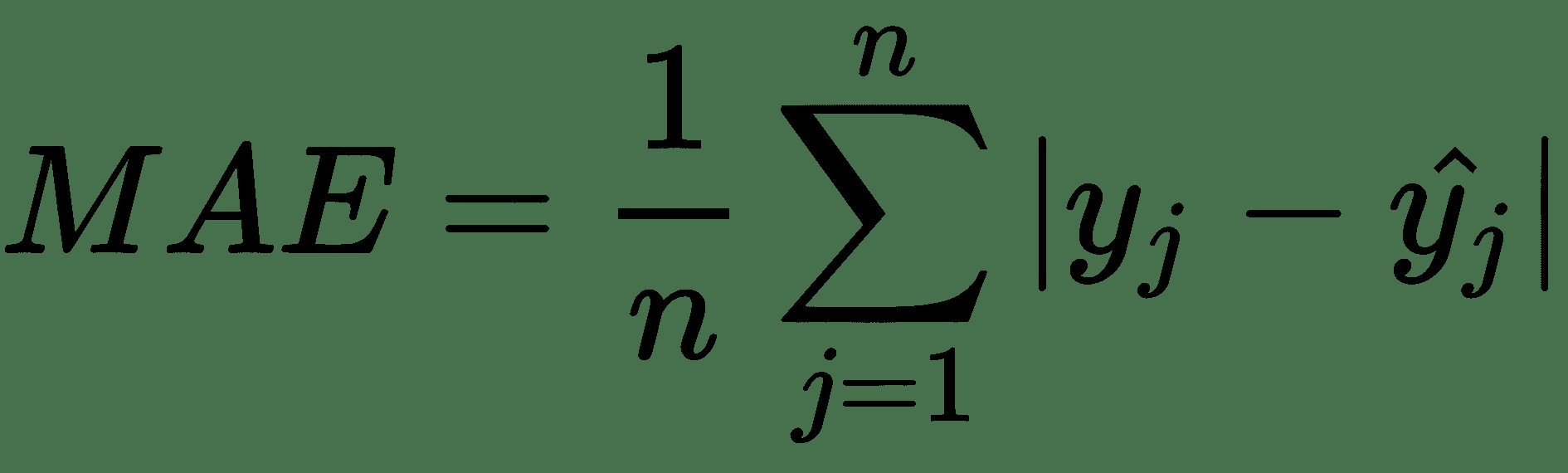 定義如下：  很簡單，MAE 是數據集中所有示例的平均無符號誤差。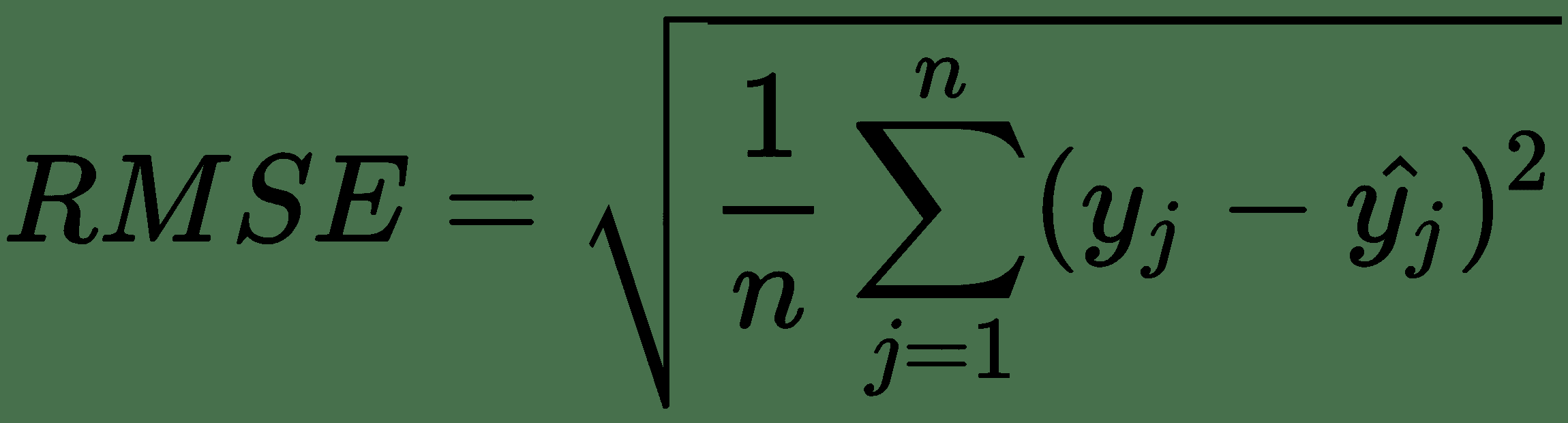 與 RMSE 非常相似； 但是，我們使用`y`和`y_hat`之間的差的絕對值代替平均平方誤差的平方根：  您可能想知道 MAE 與更熟悉??的 RMSE 有何不同。 如果誤差在數據集中均勻分布，則 RMSE 和 MAE 將相等。 如果數據集中有非常大的離群值，則 RMSE 將比 MAE 大得多。 您選擇的成本函數應適合您的用例。 關于可解釋性，MAE 比 RMSE 更具解釋性，因為它是實際的平均誤差。 # 在 Keras 中建立 MLP Keras 使用模型對象的實例來包含神經網絡。 對于熟悉 scikit-learn 的人來說，這可能是相當熟悉的。 略有不同的是 Keras 模型包含一組層。 這一組層需要由我們定義。 只需很少的代碼，就可以在網絡架構中實現驚人的靈活性。 Keras 當前有兩個用于構建模型的 API。 在我的示例中，我將使用函數式 API。 它稍微冗長一些，但可以提供更多的靈活性。 我建議盡可能使用函數式 API。 我們的 MLP 將需要一個輸入層，一個隱藏層和一個輸出層。 # 輸入層形狀 由于我們已經確定了輸入，因此我們知道輸入矩陣的行數等于數據集中的數據元素/觀測值的數量，并且列數等于變量/特征的數量。 輸入矩陣的形狀為`(觀察數量 x 10 個特征)`。 TensorFlow 和 Keras 可以在定義數據集中元素的數量時使用`None`作為占位符，而不是定義數據集中或小批量中的確切記錄數。 如果看到 Keras 或 TensorFlow 模型層形狀中使用了`None`維度，則它實際上表示任意維度，該維度可以采用任何正整數值。 # 隱藏層形狀 我們的隱藏層將從 32 個神經元開始。 在這一點上，我們不知道需要多少神經元。 這確實是一個超參數，以后可以進行探索和調整。 為給定問題確定合適的網絡架構是深度學習領域的一個開放問題。 由于隱藏層中這 32 個神經元中的每一個都將其激活輸出到輸出層，因此隱藏層的形狀將為`(10, 32)`。 # 輸出層形狀 我們的最后一層將由單個神經元組成，使用來自隱藏層的 32 個輸入，將為每個觀察值預測單個輸出值`y_hat`。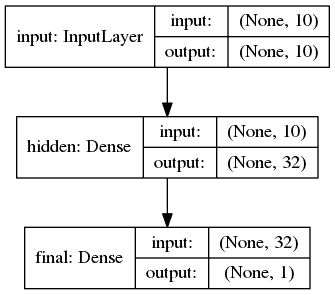 將所有各層放在一起，我們的 MLP 網絡結構將如下所示：  # 神經網絡架構 現在我們已經定義了輸入和輸出，我們可以看一下網絡的代碼。 ```py from keras.layers import Input, Dense from keras.models import Model def build_network(input_features=None): inputs = Input(shape=(input_features,), name="input") x = Dense(32, activation='relu', name="hidden")(inputs) prediction = Dense(1, activation='linear', name="final")(x) model = Model(inputs=inputs, outputs=prediction) model.compile(optimizer='adam', loss='mean_absolute_error') return model ``` 這里的所有都是它的！ 然后，我們可以使用此代碼，只需調用它即可構建適合于我們問題的神經網絡實例，如下所示： ```py model = build_network(input_features=10) ``` 但是，在開始之前，讓我們回顧一下前面代碼中的一些有趣的部分： * 每層*鏈接到*到它上面的層。 每層都是可調用的，并返回張量。 例如，當隱藏層調用它時，我們的隱藏層*綁定到輸入層*： ```py x = Dense(32, activation='relu', name="hidden")(inputs) ``` * 我們最后一層的激活函數是線性的。 這與不使用任何激活（這是我們要進行回歸）相同。 * Keras 模型需要使用`.compile()`進行編譯。 * 在編譯調用期間，您需要定義將要使用的成本函數和優化器。 正如我們所討論的，在此示例中，我已將 MAE 用于成本函數。 我使用具有默認參數的 Adam 作為我的優化程序，我們在第 1 章中已經介紹了這一點。很可能我們最終將希望調整 Adam 的學習速度。 這樣做非常簡單：您只需要定義一個自定義`adam`實例，然后使用該實例即可： ```py from keras.optimizers import Adam adam_optimizer = Adam(lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-08, decay=0.0) model.compile(optimizer=adam_optimizer, loss='mean_absolute_error') ``` # 訓練 Keras 模型 現在我們的網絡已經構建和編譯，剩下的就是訓練它了。 就像 Python 的 scikit-learn 一樣，您可以通過在模型實例上調用`.fit()`來做到這一點，如以下代碼所示： ```py model.fit(x=data["train_X"], y=data["train_y"], batch_size=32, epochs=200, verbose=1, validation_data=(data["val_X"], data["val_y"])) ``` 讓我們來看一下 Keras `fit`方法所采用的一些重要參數。 我將假設您熟悉小批量梯度下降和訓練周期，但如果不熟悉，請查看第 1 章“深度學習的基礎知識”， 概述。 Keras 擬合模型中的重要參數如下： * `batch_size`：Keras 的默認批次大小為 32。批次大小是 Keras 將使用的迷你批次的大小。 當然，這意味著 Keras 假設您要使用小批量梯度下降。 如果由于某種原因不想使用小批量梯度，可以設置`batch_size=None`。 * `epochs`：一個周期只是整個訓練集的單次通過。 在實踐中，您需要在訓練網絡時對其進行監視，以了解網絡何時收斂，因此`epochs`是一個易于學習的超參數。 稍后，我們將看到可以在每個周期甚至比最后一個周期更好的每個周期保存模型的權重。 一旦知道如何做到這一點，我們就可以選擇我們認為最好的周期，并實現一種基于人的早期停止。 * `validation_data`：在這里，我們指定驗證集。 在每個階段結束時，Keras 將在驗證集上測試模型，并使用損失函數和您指定的任何其他指標輸出結果。 另外，您可以將`validation_split`設置為浮點值，以指定要用于驗證的訓練組的百分比。 這兩個選項都可以正常工作，但是在數據集拆分方面，我希望講得很明確。 * `verbose`：這有點不言而喻； 但是，值得一提。 `verbose=1`輸出一個進度條，顯示當前周期的狀態，在周期結束時，Keras 將輸出訓練和驗證損失。 也可以將`verbose`設置為 2（每個小批量輸出損失信息），將其設置為 0（使 Keras 保持靜音）。 # 評估模型的表現 現在我們的 MLP 已經過訓練，我們可以開始了解它的表現。 為此，我將對`Train`，`Val`和`Test`數據集進行預測。 相同的代碼如下： ```py print("Model Train MAE: " + str(mean_absolute_error(data["train_y"], model.predict(data["train_X"])))) print("Model Val MAE: " + str(mean_absolute_error(data["val_y"], model.predict(data["val_X"])))) print("Model Test MAE: " + str(mean_absolute_error(data["test_y"], model.predict(data["test_X"])))) ``` 對于我們的 MLP，這是我們做得如何： ```py Model Train MAE: 0.190074701809 Model Val MAE: 0.213255747475 Model Test MAE: 0.199885450841 ``` 請記住，我們的數據已縮放為 0 均值和單位方差。 `Train MAE`是`0.19`，而我們的`Val MAE`是`0.21`。 這兩個誤差彼此之間非常接近，所以過分適合并不是我太在意的事情。 因為我預計會有一些我看不到的過擬合（通常是更大的問題），所以我認為此模型可能有太多偏差。 換句話說，我們可能無法足夠緊密地擬合數據。 發生這種情況時，我們需要為我們的模型添加更多的層，更多的神經元或兩者。 我們需要更深入。 讓我們接下來做。 我們可以嘗試通過以更多神經元的形式向網絡添加參數來減少網絡偏差。 雖然您可能會開始嘗試優化優化器，但通常最好先找到自己熟悉的網絡架構。 # 在 Keras 中建立深度神經網絡 更改模型就像重新定義我們先前的`build_network()`函數一樣容易。 我們的輸入層將保持不變，因為我們的輸入沒有更改。 同樣，輸出層應保持不變。 我將通過添加其他隱藏層將參數添加到我們的網絡中。 我希望通過添加這些隱藏層，我們的網絡可以了解輸入和輸出之間更復雜的關系。 我將從添加四個其他隱藏層開始； 前三個將具有 32 個神經元，第四個將具有 16 個神經元。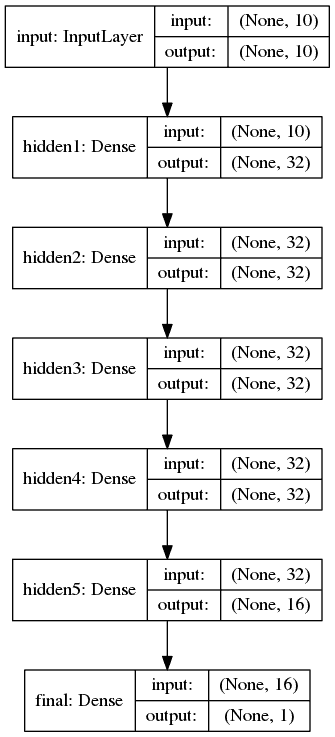其外觀如下：  以下是在 Keras 中構建模型的相關代碼： ```py def build_network(input_features=None): inputs = Input(shape=(input_features,), name="input") x = Dense(32, activation='relu', name="hidden1")(inputs) x = Dense(32, activation='relu', name="hidden2")(x) x = Dense(32, activation='relu', name="hidden3")(x) x = Dense(32, activation='relu', name="hidden4")(x) x = Dense(16, activation='relu', name="hidden5")(x) prediction = Dense(1, activation='linear', name="final")(x) model = Model(inputs=inputs, outputs=prediction) model.compile(optimizer='adam', loss='mean_absolute_error') return model ``` 如所承諾的，我們的代碼幾乎沒有改變。 我將其他行加粗了。 我們其余的代碼可以保持不變。 但是，隨著網絡復雜性的增加，您通常必須訓練更長的時間（更多的時間）。 # 測量深度神經網絡表現 在這個問題上，深層網絡真的比 MLP 好嗎？ 讓我們找出答案！ 訓練了 500 個周期后，模型的效果如下： ```py Model Train MAE: 0.0753991873787 Model Val MAE: 0.189703853999 Model Test MAE: 0.190189985043 ``` 我們可以看到`Train MAE`現在從`0.19`減少到`0.075`。 我們大大降低了網絡的偏差。 但是，我們的差異增加了。 訓練誤差和驗證誤差之間的差異要大得多。 我們的`Val`集誤差確實略有下降，這很好； 但是，訓練誤差和驗證誤差之間的巨大差距表明我們開始過度適應訓練集。 在這種情況下，減少差異的最直接方法是添加其他訓練數據或應用諸如 L2 正則化或丟棄法之類的正則化技術，我們將在下一章中介紹。 對于高方差網絡，更多的數據通常是最佳解決方案。 如果有可能收集更多數據，那可能就是花費時間的最佳位置。 建立網絡后，我想直觀地檢查誤差，以了解網絡對驗證集分布進行建模的程度。 這通常會帶來見解，這將有助于我改進模型。 對于回歸模型，我想繪制驗證集的預測值和實際值的直方圖。 讓我們看看我的表現如何。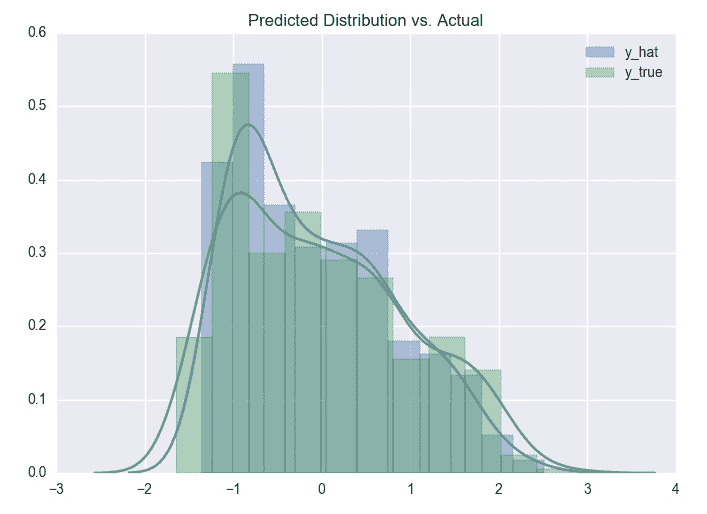 該圖如下，供您參考：  總體而言，我認為該模型正在相當接近地預測實際分布。 似乎實際的驗證數據集比預測的數據集向左移動（較小的值）要多一些，這可能是一個重要的見解。 換句話說，網絡可能會預測葡萄酒的酒精含量高于平均水平，尤其是在酒精含量較低的情況下。 更仔細地檢查驗證數據可能會建議我們如何收集更多的訓練數據。 # 調整模型超參數 現在，我們已經針對該問題訓練了 MLP 和六層深度神經網絡，現在可以調整和優化模型超參數了。 我們將在第 6 章“超參數優化”中討論深度模型調整。 您可以使用多種策略為模型選擇最佳參數。 您可能已經注意到，我們仍然可以優化許多可能的參數和超參數。 如果要完全調整此模型，則應執行以下操作： * 試驗隱藏層的數量。 看來五個可能太多，而一個可能還不夠。 * 試驗每個隱藏層相對于層數的神經元數量。 * 嘗試添加丟棄或正則化。 * 嘗試通過嘗試使用 SGD 或 RMS 屬性而不是 Adam 或通過對 Adam 使用不同的學習率來進一步減少模型誤差。 深度神經網絡有許多活動部分，有時要達到最佳狀態是一個疲憊的概念。 您必須確定您的模型是否足夠好。 # 保存和加載經過訓練的 Keras 模型 您不太可能會訓練一個深層的神經網絡，然后將其應用到同一腳本中。 最有可能的是，您將需要訓練網絡，然后保存結構和權重，以便可以將其用于設計用于對新數據進行評分的面向生產的應用中。 為此，您需要能夠保存和加載模型。 在 Keras 中保存模型非常簡單。 您可以使用模型實例的`.save()`方法將網絡結構和權重保存到`hdf5`文件，如以下代碼所示： ```py model.save("regression_model.h5") ``` 這就是全部。 從磁盤加載模型非常簡單。 此處提供了執行此操作的代碼供您參考： ```py from keras.models import load_model model = load_model("regression_model.h5") ``` # 總結 當您考慮深度學習時，您可能會想到令人印象深刻的復雜計算機視覺問題，但是即使對于像這樣的簡單回歸問題，深度神經網絡也可能有用。 希望我已經證明了這一點，同時還介紹了 Keras 語法并向您展示了如何構建一個非常簡單的網絡。 隨著我們的繼續，我們將遇到更多的復雜性。 更大的網絡，更復雜的成本函數以及高維輸入數據。 但是，我在本章中使用的過程在大多數情況下將保持不變。 在每種情況下，我們都將概述問題，確定輸入和輸出，選擇成本函數，創建網絡架構，最后訓練和調整模型。 如果考慮以下因素，則在深度神經網絡中通常可以獨立地控制和減少偏差和方差： * **偏差**：可以通過增加模型復雜度來減少此偏差。 其他神經元或層將有所幫助。 添加數據并不能真正幫助減少偏差。 * **方差**：可以通過添加數據或正則化來減少此變化。 在下一章中，我們將討論如何使用 TensorBoard 更快地對深度神經網絡進行優化和故障排除。