# 九、TensorFlow 和 Keras 中的 CNN **卷積神經網絡**（**CNN**）是一種特殊的前饋神經網絡，在其架構中包含卷積和匯聚層。也稱為 ConvNets，CNN 架構的一般模式是按以下順序包含這些層： 1. 完全連接的輸入層 2. 卷積，池化和全連接層的多種組合 3. 完全連接的輸出層，具有 softmax 激活函數 CNN 架構已被證明在解決涉及圖像學習的問題（例如圖像識別和對象識別）方面非常成功。 在本章中，我們將學習與卷積網絡相關的以下主題： * 理解卷積 * 理解池化 * CNN 架構模式 - LeNet * 用于 MNIST 數據集的 LeNet * 使用 TensorFlow 和 MNIST 的 LeNet * 使用 Keras 和 MNIST 的 LeNet * 用于 CIFAR 數據集的 LeNet * 使用 TensorFlow 和 CIFAR10 的 LeNet CNN * 使用 Keras 和 CIFAR10 的 LeNet CNN 讓我們從學習卷積網絡背后的核心概念開始。 # 理解卷積 **卷積**是 CNN 架構背后的核心概念。簡單來說，卷積是一種數學運算，它結合了兩個來源的信息來產生一組新的信息。具體來說，它將一個稱為內核的特殊矩陣應用于輸入張量，以產生一組稱為特征圖的矩陣。可以使用任何流行的算法將內核應用于輸入張量。 生成卷積矩陣的最常用算法如下： ```py N_STRIDES = [1,1] 1\. Overlap the kernel with the top-left cells of the image matrix. 2\. Repeat while the kernel overlaps the image matrix: 2.1 c_col = 0 2.2 Repeat while the kernel overlaps the image matrix: 2.1.1 set c_row = 0 2.1.2 convolved_scalar = scalar_prod(kernel, overlapped cells) 2.1.3 convolved_matrix(c_row,c_col) = convolved_scalar 2.1.4 Slide the kernel down by N_STRIDES[0] rows. 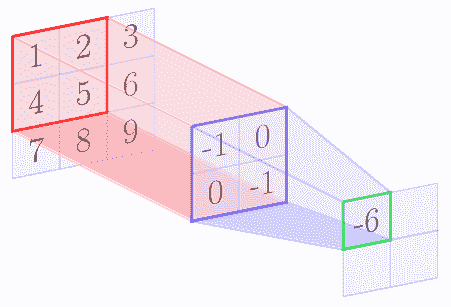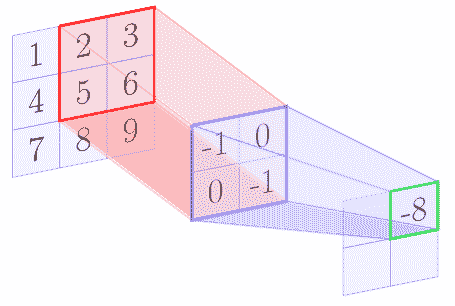2.1.5 c_row = c_row + 1 2.3 Slide the kernel to (topmost row, N_STRIDES[1] columns right) 2.4 c_col = c_col + 1 ``` 例如，我們假設核矩陣是`2 x 2`矩陣，輸入圖像是`3 x 3`矩陣。下圖逐步顯示了上述算法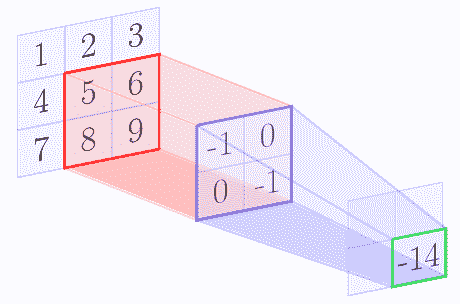： | | | | --- | --- | |  |  | |  |  | 在卷積操作結束時，我們得到以下特征圖： | | | | --- | --- | | -6 | -8 | | -12 | -14 | 在上面的示例中，與卷積的原始輸入相比，生成的特征映射的大小更小。通常，特征圖的大小減小（內核大小減 1）。因此，特征圖的大小為：  **三維張量** 對于具有額外深度尺寸的三維張量，您可以將前面的算法視為應用于深度維度中的每個層。將卷積應用于 3D 張量的輸出也是 2D 張量，因為卷積運算添加了三個通道。 **步幅** 數組`N_STRIDES`中的**步長**是您想要將內核滑過的行或列的數字。在我們的例子中，我們使用了 1 的步幅。如果我們使用更多的步幅，那么特征圖的大小將根據以下等式進一步減小：  **填充** 如果我們不希望減小特征映射的大小，那么我們可以在輸入的所有邊上使用填充，使得特征的大小增加填充大小的兩倍。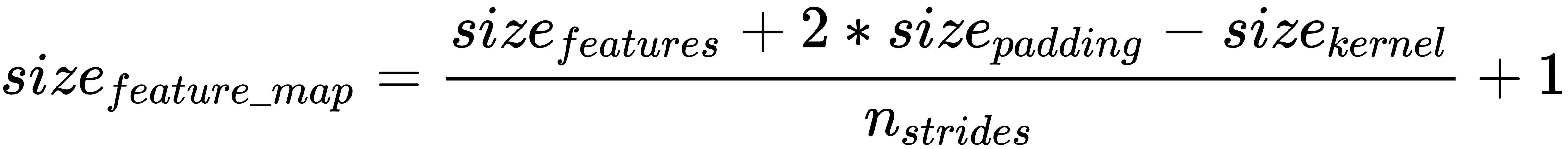使用填充，可以按如下方式計算特征圖的大小：  TensorFlow 允許兩種填充：`SAME`或`VALID`。 `SAME`填充意味著添加填充，使輸出特征圖與輸入特征具有相同的大小。 `VALID`填充意味著沒有填充。 應用前面提到的卷積算法的結果是特征圖，是原始張量的濾波版本。例如，特征圖可能只有從原始圖像中過濾出的輪廓。因此，內核也稱為過濾器。對于每個內核，您將獲得單獨的 2D 特征圖。 根據您希望網絡學習的特征，您必須應用適當的過濾器來強調所需的特征。 但是，使用 CNN，模型可以自動了解哪些內核在卷積層中最有效。 **TensorFlow** 中的卷積運算 TensorFlow 提供實現卷積算法的卷積層。例如，具有以下簽名的`tf.nn.conv2d()`操作： ```py tf.nn.conv2d( input, filter, strides, padding, use_cudnn_on_gpu=None, data_format=None, name=None ) ``` `input`和`filter`表示形狀`[batch_size, input_height, input_width, input_depth]`的數據張量和形狀`[filter_height, filter_width, input_depth, output_depth]`的核張量。內核張量中的`output_depth`表示應該應用于輸入的內核數量。`strides`張量表示每個維度中要滑動的單元數。如上所述，`padding`是有效的或相同的。 [您可以在此鏈接中找到有關 TensorFlow 中可用卷積操作的更多信息](https://www.tensorflow.org/api_guides/python/nn#Convolution) [您可以在此鏈接中找到有關 Keras 中可用卷積層的更多信息](https://keras.io/layers/convolutional/) 此鏈接提供了卷積的詳細數學解釋： <http://colah.github.io/posts/2014-07-Understanding-Convolutions/> <http://ufldl.stanford.edu/tutorial/supervised/FeatureExtractionUsingConvolution/> <http://colah.github.io/posts/2014-07-Understanding-Convolutions/> 卷積層或操作將輸入值或神經元連接到下一個隱藏層神經元。每個隱藏層神經元連接到與內核中元素數量相同數量的輸入神經元。所以在前面的例子中，內核有 4 個元素，因此隱藏層神經元連接到輸入層的 4 個神經元（`3×3` 個神經元中）。在我們的例子中，輸入層的 4 個神經元的這個區域被稱為 CNN 理論中的**感受域**。 卷積層具有每個內核的單獨權重和偏差參數。權重參數的數量等于內核中元素的數量，并且只有一個偏差參數。內核的所有連接共享相同的權重和偏差參數。因此在我們的例子中，將有 4 個權重參數和 1 個偏差參數，但如果我們在卷積層中使用 5 個內核，則總共將有`5 x 4`個權重參數和`5 x 1`個偏差參數（每個特征圖 4 個權重，1 個偏差）。 # 理解池化 通常，在卷積操作中，應用幾個不同的內核，這導致生成若干特征映射。因此，卷積運算導致生成大尺寸數據集。 例如，將形狀為`3 x 3 x 1`的內核應用于具有`28 x 28 x 1`像素形狀的圖像的 MNIST 數據集，可生成形狀為`26 x 26 x 1`的特征映射。如果我們在其中應用 32 個這樣的濾波器卷積層，則輸出的形狀為`32 x 26 x 26 x 1`，即形狀為`26 x 26 x 1`的 32 個特征圖。 與形狀為`28 x 28 x 1`的原始數據集相比，這是一個龐大的數據集。因此，為了簡化下一層的學習，我們應用池化的概念。 **聚合**是指計算卷積特征空間區域的聚合統計量。兩個最受歡迎的聚合統計數據是最大值和平均值。應用最大池化的輸出是所選區域的最大值，而應用平均池的輸出是區域中數字的平均值。 例如，假設特征圖的形狀為`3 x 3`，池化區域形狀為`2 x 2`。以下圖像顯示了使用`[1, 1]`的步幅應用的最大池操作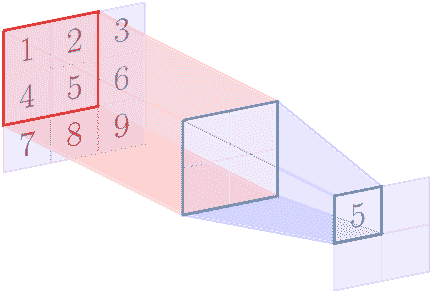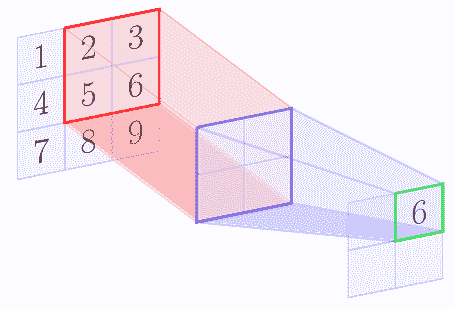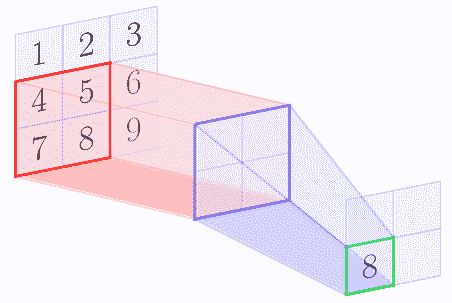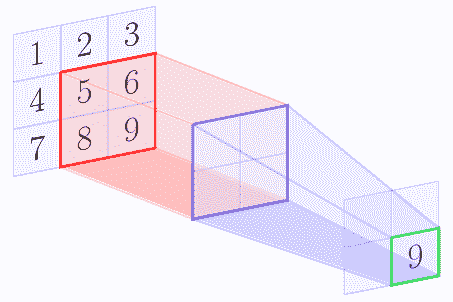： | | | | --- | --- | |  |  | |  |  | 在最大池操作結束時，我們得到以下矩陣： | | | | --- | --- | | 5 | 6 | | 8 | 9 | 通常，池化操作應用非重疊區域，因此步幅張量和區域張量被設置為相同的值。 例如，TensorFlow 具有以下簽名的`max_pooling`操作： ```py max_pool( value, ksize, strides, padding, data_format='NHWC', name=None ) ``` `value`表示形狀`[batch_size, input_height, input_width, input_depth]`的輸入張量。對矩形形狀區域`ksize`執行合并操作。這些區域被形狀`strides`抵消。 [您可以在此鏈接中找到有關 TensorFlow 中可用的池化操作的更多信息](https://www.tensorflow.org/api_guides/python/nn#Pooling) [有關 Keras 中可用池化的更多信息，請訪問此鏈接](https://keras.io/layers/pooling/) [此鏈接提供了池化的詳細數學說明](http://ufldl.stanford.edu/tutorial/supervised/Pooling/) # CNN 架構模式 - LeNet LeNet 是實現 CNN 的流行架構模式。在本章中，我們將學習如何通過按以下順序創建層來構建基于 LeNet 模式的 CNN 模型： 1. 輸入層 2. 卷積層 1，它產生一組特征映射，具有 ReLU 激活 3. 池化層 1 產生一組統計聚合的特征映射 4. 卷積層 2，其產生一組特征映射，具有 ReLU 激活 5. 池化層 2 產生一組統計聚合的特征映射 6. 完全連接的層，通過 ReLU 激活來展平特征圖 7. 通過應用簡單線性激活產生輸出的輸出層 **LeNet** 系列模型由 Yann LeCun 及其研究員介紹。有關 LeNet 系列模型的更多詳細信息，[請訪問此鏈接](http://yann.lecun.com/exdb/publis/pdf/lecun-01a.pdf)。 [Yann LeCun 通過此鏈接維護 LeNet 系列模型列表](http://yann.lecun.com/exdb/lenet/index.html)。 # 用于 MNIST 數據的 LeNet 您可以按照 Jupyter 筆記本中的代碼`ch-09a_CNN_MNIST_TF_and_Keras`。 準備 MNIST 數據到測試和訓練集： ```py from tensorflow.examples.tutorials.mnist import input_data mnist = input_data.read_data_sets(os.path.join('.','mnist'), one_hot=True) X_train = mnist.train.images X_test = mnist.test.images Y_train = mnist.train.labels Y_test = mnist.test.labels ``` # TensorFlow 中的用于 MNIST 的 LeNet CNN 在 TensorFlow 中，應用以下步驟為 MNIST 數據構建基于 LeNet 的 CNN 模型： 1. 定義超參數，以及 x 和 y 的占位符（輸入圖像和輸出標簽） ： ```py n_classes = 10 # 0-9 digits n_width = 28 n_height = 28 n_depth = 1 n_inputs = n_height * n_width * n_depth # total pixels learning_rate = 0.001 n_epochs = 10 batch_size = 100 n_batches = int(mnist.train.num_examples/batch_size) # input images shape: (n_samples,n_pixels) x = tf.placeholder(dtype=tf.float32, name="x", shape=[None, n_inputs]) # output labels y = tf.placeholder(dtype=tf.float32, name="y", shape=[None, n_classes]) ``` 將輸入 x 重塑為形狀`(n_samples, n_width, n_height, n_depth)`： ```py x_ = tf.reshape(x, shape=[-1, n_width, n_height, n_depth]) ``` 1. 使用形狀為`4 x 4`的 32 個內核定義第一個卷積層，從而生成 32 個特征圖。 * 首先，定義第一個卷積層的權重和偏差。我們使用正態分布填充參數： ```py layer1_w = tf.Variable(tf.random_normal(shape=[4,4,n_depth,32], stddev=0.1),name='l1_w') layer1_b = tf.Variable(tf.random_normal([32]),name='l1_b') ``` * 接下來，用`tf.nn.conv2d`函數定義卷積層。函數參數`stride`定義了內核張量在每個維度中應該滑動的元素。維度順序由`data_format`確定，可以是`'NHWC'`或`'NCHW'`（默認為`'NHWC'`）。 通常，`stride`中的第一個和最后一個元素設置為 1。函數參數`padding`可以是`SAME`或`VALID`。`SAME` `padding`表示輸入將用零填充，以便在卷積后輸出與輸入的形狀相同。使用`tf.nn.relu()`函數添加`relu`激活： ```py layer1_conv = tf.nn.relu(tf.nn.conv2d(x_,layer1_w, strides=[1,1,1,1], padding='SAME' ) + layer1_b ) ``` * 使用`tf.nn.max_pool()`函數定義第一個池化層。參數`ksize`表示使用`2×2×1`個區域的合并操作，參數`stride`表示將區域滑動`2×2×1`個像素。因此，區域彼此不重疊。由于我們使用`max_pool`，池化操作選擇`2 x 2 x 1`區域中的最大值： ```py layer1_pool = tf.nn.max_pool(layer1_conv,ksize=[1,2,2,1], strides=[1,2,2,1],padding='SAME') ``` 第一個卷積層產生 32 個大小為`28 x 28 x 1`的特征圖，然后池化成`32 x 14 x 14 x 1`的數據。 1. 定義第二個卷積層，它將此數據作為輸入并生成 64 個特征圖。 * 首先，定義第二個卷積層的權重和偏差。我們用正態分布填充參數： ```py layer2_w = tf.Variable(tf.random_normal(shape=[4,4,32,64], stddev=0.1),name='l2_w') layer2_b = tf.Variable(tf.random_normal([64]),name='l2_b') ``` * 接下來，用`tf.nn.conv2d`函數定義卷積層： ```py layer2_conv = tf.nn.relu(tf.nn.conv2d(layer1_pool, layer2_w, strides=[1,1,1,1], padding='SAME' ) + layer2_b ) ``` * 用`tf.nn.max_pool`函數定義第二個池化層： ```py layer2_pool = tf.nn.max_pool(layer2_conv, ksize=[1,2,2,1], strides=[1,2,2,1], padding='SAME' ) ``` 第二卷積層的輸出形狀為`64×14×14×1`，然后池化成`64×7×7×1`的形狀的輸出。 1. 在輸入 1024 個神經元的完全連接層之前重新整形此輸出，以產生大小為 1024 的扁平輸出： ```py layer3_w = tf.Variable(tf.random_normal(shape=[64*7*7*1,1024], stddev=0.1),name='l3_w') layer3_b = tf.Variable(tf.random_normal([1024]),name='l3_b') layer3_fc = tf.nn.relu(tf.matmul(tf.reshape(layer2_pool, [-1, 64*7*7*1]),layer3_w) + layer3_b) ``` 1. 完全連接層的輸出饋入具有 10 個輸出的線性輸出層。我們在這一層沒有使用 softmax，因為我們的損失函數自動將 softmax 應用于輸出： ```py layer4_w = tf.Variable(tf.random_normal(shape=[1024, n_classes], stddev=0.1),name='l) layer4_b = tf.Variable(tf.random_normal([n_classes]),name='l4_b') layer4_out = tf.matmul(layer3_fc,layer4_w)+layer4_b ``` 這創建了我們保存在變量`model`中的第一個 CNN 模型： ```py model = layer4_out ``` 鼓勵讀者探索具有不同超參數值的 TensorFlow 中可用的不同卷積和池操作符。 為了定義損失，我們使用`tf.nn.softmax_cross_entropy_with_logits`函數，對于優化器，我們使用`AdamOptimizer`函數。您應該嘗試探索 TensorFlow 中可用的不同優化器函數。 ```py entropy = tf.nn.softmax_cross_entropy_with_logits(logits=model, labels=y) loss = tf.reduce_mean(entropy) optimizer = tf.train.AdamOptimizer(learning_rate).minimize(loss) ``` 最后，我們通過迭代`n_epochs`來訓練模型，并且在`n_batches`上的每個周期列中，每批`batch_size`的大小： ```py with tf.Session() as tfs: tf.global_variables_initializer().run() for epoch in range(n_epochs): total_loss = 0.0 for batch in range(n_batches): batch_x,batch_y = mnist.train.next_batch(batch_size) feed_dict={x:batch_x, y: batch_y} batch_loss,_ = tfs.run([loss, optimizer], feed_dict=feed_dict) total_loss += batch_loss average_loss = total_loss / n_batches print("Epoch: {0:04d} loss = {1:0.6f}".format(epoch,average_loss)) print("Model Trained.") predictions_check = tf.equal(tf.argmax(model,1),tf.argmax(y,1)) accuracy = tf.reduce_mean(tf.cast(predictions_check, tf.float32)) feed_dict = {x:mnist.test.images, y:mnist.test.labels} print("Accuracy:", accuracy.eval(feed_dict=feed_dict)) ``` 我們得到以下輸出： ```py Epoch: 0000 loss = 1.418295 Epoch: 0001 loss = 0.088259 Epoch: 0002 loss = 0.055410 Epoch: 0003 loss = 0.042798 Epoch: 0004 loss = 0.030471 Epoch: 0005 loss = 0.023837 Epoch: 0006 loss = 0.019800 Epoch: 0007 loss = 0.015900 Epoch: 0008 loss = 0.012918 Epoch: 0009 loss = 0.010322 Model Trained. Accuracy: 0.9884 ``` 現在，與我們在前幾章中看到的方法相比，這是一個非常好的準確率。從圖像數據中學習 CNN 模型是不是很神奇？ # Keras 中的用于 MNIST 的 LeNet CNN 讓我們重新審視具有相同數據集的相同 LeNet 架構，以在 Keras 中構建和訓練 CNN 模型： 1. 導入所需的 Keras 模塊： ```py import keras from keras.models import Sequential from keras.layers import Conv2D,MaxPooling2D, Dense, Flatten, Reshape from keras.optimizers import SGD ``` 1. 定義每個層的過濾器數量： ```py n_filters=[32,64] ``` 1. 定義其他超參數： ```py learning_rate = 0.01 n_epochs = 10 batch_size = 100 ``` 1. 定義順序模型并添加層以將輸入數據重新整形為形狀`(n_width,n_height,n_depth)`： ```py model = Sequential() model.add(Reshape(target_shape=(n_width,n_height,n_depth), input_shape=(n_inputs,)) ) ``` 1. 使用`4 x 4`內核過濾器，`SAME`填充和`relu`激活添加第一個卷積層： ```py model.add(Conv2D(filters=n_filters[0],kernel_size=4, padding='SAME',activation='relu') ) ``` 1. 添加區域大小為`2 x 2`且步長為`2 x 2`的池化層： ```py model.add(MaxPooling2D(pool_size=(2,2),strides=(2,2))) ``` 1. 以與添加第一層相同的方式添加第二個卷積和池化層： ```py model.add(Conv2D(filters=n_filters[1],kernel_size=4, padding='SAME',activation='relu') ) model.add(MaxPooling2D(pool_size=(2,2),strides=(2,2))) ``` 1. 添加層以展平第二個層的輸出和 1024 個神經元的完全連接層，以處理展平的輸出： ```py model.add(Flatten()) model.add(Dense(units=1024, activation='relu')) ``` 1. 使用`softmax`激活添加最終輸出層： ```py model.add(Dense(units=n_outputs, activation='softmax')) ``` 1. 使用以下代碼查看模型摘要： ```py model.summary() ``` 該模型描述如下： ```py Layer (type) Output Shape Param # ================================================================= reshape_1 (Reshape) (None, 28, 28, 1) 0 _________________________________________________________________ conv2d_1 (Conv2D) (None, 28, 28, 32) 544 _________________________________________________________________ max_pooling2d_1 (MaxPooling2 (None, 14, 14, 32) 0 _________________________________________________________________ conv2d_2 (Conv2D) (None, 14, 14, 64) 32832 _________________________________________________________________ max_pooling2d_2 (MaxPooling2 (None, 7, 7, 64) 0 _________________________________________________________________ flatten_1 (Flatten) (None, 3136) 0 _________________________________________________________________ dense_1 (Dense) (None, 1024) 3212288 _________________________________________________________________ dense_2 (Dense) (None, 10) 10250 ================================================================= Total params: 3,255,914 Trainable params: 3,255,914 Non-trainable params: 0 _________________________________________________________________ ``` 1. 編譯，訓練和評估模型： ```py model.compile(loss='categorical_crossentropy', optimizer=SGD(lr=learning_rate), metrics=['accuracy']) model.fit(X_train, Y_train,batch_size=batch_size, epochs=n_epochs) score = model.evaluate(X_test, Y_test) print('\nTest loss:', score[0]) print('Test accuracy:', score[1]) ``` 我們得到以下輸出： ```py Epoch 1/10 55000/55000 [===================] - 267s - loss: 0.8854 - acc: 0.7631 Epoch 2/10 55000/55000 [===================] - 272s - loss: 0.2406 - acc: 0.9272 Epoch 3/10 55000/55000 [===================] - 267s - loss: 0.1712 - acc: 0.9488 Epoch 4/10 55000/55000 [===================] - 295s - loss: 0.1339 - acc: 0.9604 Epoch 5/10 55000/55000 [===================] - 278s - loss: 0.1112 - acc: 0.9667 Epoch 6/10 55000/55000 [===================] - 279s - loss: 0.0957 - acc: 0.9714 Epoch 7/10 55000/55000 [===================] - 316s - loss: 0.0842 - acc: 0.9744 Epoch 8/10 55000/55000 [===================] - 317s - loss: 0.0758 - acc: 0.9773 Epoch 9/10 55000/55000 [===================] - 285s - loss: 0.0693 - acc: 0.9790 Epoch 10/10 55000/55000 [===================] - 217s - loss: 0.0630 - acc: 0.9804 Test loss: 0.0628845927377 Test accuracy: 0.9785 ``` 準確率的差異可歸因于我們在這里使用 SGD 優化器這一事實，它沒有實現我們用于 TensorFlow 模型的`AdamOptimizer`提供的一些高級功能。 # 用于 CIFAR10 數據的 LeNet 現在我們已經學會了使用 TensorFlow 和 Keras 的 MNIST 數據集構建和訓練 CNN 模型，讓我們用 CIFAR10 數據集重復練習。 CIFAR-10 數據集包含 60,000 個`32x32`像素形狀的 RGB 彩色圖像。圖像被平均分為 10 個不同的類別或類別：飛機，汽車，鳥，貓，鹿，狗，青蛙，馬，船和卡車。 CIFAR-10 和 CIFAR-100 是包含 8000 萬個圖像的大圖像數據集的子集。 CIFAR 數據集由 Alex Krizhevsky，Vinod Nair 和 Geoffrey Hinton 收集和標記。數字 10 和 100 表示??圖像類別的數量。 有關 CIFAR 數據集的更多詳細信息，請訪問此鏈接： <http://www.cs.toronto.edu/~kriz/cifar.html> 和 <http://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf> 我們選擇了 CIFAR 10，因為它有 3 個通道，即圖像的深度為 3，而 MNIST 數據集只有一個通道。 為了簡潔起見，我們將詳細信息留給下載并將數據拆分為訓練和測試集，并在本書代碼包中的`datasetslib`包中提供代碼。 您可以按照 Jupyter 筆記本中的代碼`ch-09b_CNN_CIFAR10_TF_and_Keras`。 我們使用以下代碼加載和預處理 CIFAR10 數據： ```py from datasetslib.cifar import cifar10 from datasetslib import imutil dataset = cifar10() dataset.x_layout=imutil.LAYOUT_NHWC dataset.load_data() dataset.scaleX() ``` 加載數據使得圖像采用`'NHWC'`格式，使數據變形（`number_of_samples, image_height, image_width, image_channels`）。我們將圖像通道稱為圖像深度。圖像中的每個像素是 0 到 255 之間的數字。使用 MinMax 縮放來縮放數據集，以通過將所有像素值除以 255 來標準化圖像。 加載和預處理的數據在數據集對象變量中可用作`dataset.X_train`，`dataset.Y_train`，`dataset.X_test`和`dataset.Y_test`。 # TensorFlow 中的用于 CIFAR10 的卷積網絡 我們保持層，濾波器及其大小與之前的 MNIST 示例中的相同，增加了一個正則化層。由于此數據集與 MNIST 相比較復雜，因此我們為正則化目的添加了額外的丟棄層： ```py tf.nn.dropout(layer1_pool, keep_prob) ``` 在預測和評估期間，占位符`keep_prob`設置為 1。這樣我們就可以重復使用相同的模型進行訓練以及預測和評估。 有關 CIFAR10 數據的 LeNet 模型的完整代碼在筆記本`ch-09b_CNN_CIFAR10_TF_and_Keras`中提供。 在運行模型時，我們得到以下輸出： ```py Epoch: 0000 loss = 2.115784 Epoch: 0001 loss = 1.620117 Epoch: 0002 loss = 1.417657 Epoch: 0003 loss = 1.284346 Epoch: 0004 loss = 1.164068 Epoch: 0005 loss = 1.058837 Epoch: 0006 loss = 0.953583 Epoch: 0007 loss = 0.853759 Epoch: 0008 loss = 0.758431 Epoch: 0009 loss = 0.663844 Epoch: 0010 loss = 0.574547 Epoch: 0011 loss = 0.489902 Epoch: 0012 loss = 0.410211 Epoch: 0013 loss = 0.342640 Epoch: 0014 loss = 0.280877 Epoch: 0015 loss = 0.234057 Epoch: 0016 loss = 0.195667 Epoch: 0017 loss = 0.161439 Epoch: 0018 loss = 0.140618 Epoch: 0019 loss = 0.126363 Model Trained. Accuracy: 0.6361 ``` 與我們在 MNIST 數據上獲得的準確率相比，我們沒有獲得良好的準確率。通過調整不同的超參數并改變卷積和池化層的組合，可以實現更好的準確率。我們將其作為挑戰，讓讀者探索并嘗試不同的 LeNet 架構和超參數變體，以實現更高的準確率。 # Keras 中的用于 CIFAR10 的卷積網絡 讓我們在 Keras 重復 LeNet CNN 模型構建和 CIFAR10 數據訓練。我們保持架構與前面的示例相同，以便輕松解釋概念。在 Keras 中，丟棄層添加如下： ```py model.add(Dropout(0.2)) ``` 用于 CIFAR10 CNN 模型的 Keras 中的完整代碼在筆記本`ch-09b_CNN_CIFAR10_TF_and_Keras`中提供。 在運行模型時，我們得到以下模型描述： ```py _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d_1 (Conv2D) (None, 32, 32, 32) 1568 _________________________________________________________________ max_pooling2d_1 (MaxPooling2 (None, 16, 16, 32) 0 _________________________________________________________________ dropout_1 (Dropout) (None, 16, 16, 32) 0 _________________________________________________________________ conv2d_2 (Conv2D) (None, 16, 16, 64) 32832 _________________________________________________________________ max_pooling2d_2 (MaxPooling2 (None, 8, 8, 64) 0 _________________________________________________________________ dropout_2 (Dropout) (None, 8, 8, 64) 0 _________________________________________________________________ flatten_1 (Flatten) (None, 4096) 0 _________________________________________________________________ dense_1 (Dense) (None, 1024) 4195328 _________________________________________________________________ dropout_3 (Dropout) (None, 1024) 0 _________________________________________________________________ dense_2 (Dense) (None, 10) 10250 ================================================================= Total params: 4,239,978 Trainable params: 4,239,978 Non-trainable params: 0 _________________________________________________________________ ``` 我們得到以下訓練和評估結果： ```py Epoch 1/10 50000/50000 [====================] - 191s - loss: 1.5847 - acc: 0.4364 Epoch 2/10 50000/50000 [====================] - 202s - loss: 1.1491 - acc: 0.5973 Epoch 3/10 50000/50000 [====================] - 223s - loss: 0.9838 - acc: 0.6582 Epoch 4/10 50000/50000 [====================] - 223s - loss: 0.8612 - acc: 0.7009 Epoch 5/10 50000/50000 [====================] - 224s - loss: 0.7564 - acc: 0.7394 Epoch 6/10 50000/50000 [====================] - 217s - loss: 0.6690 - acc: 0.7710 Epoch 7/10 50000/50000 [====================] - 222s - loss: 0.5925 - acc: 0.7945 Epoch 8/10 50000/50000 [====================] - 221s - loss: 0.5263 - acc: 0.8191 Epoch 9/10 50000/50000 [====================] - 237s - loss: 0.4692 - acc: 0.8387 Epoch 10/10 50000/50000 [====================] - 230s - loss: 0.4320 - acc: 0.8528 Test loss: 0.849927025414 Test accuracy: 0.7414 ``` 再次，我們將其作為挑戰，讓讀者探索并嘗試不同的 LeNet 架構和超參數變體，以實現更高的準確率。 # 總結 在本章中，我們學習了如何使用 TensorFlow 和 Keras 創建卷積神經網絡。我們學習了卷積和池化的核心概念，這是 CNN 的基礎。我們學習了 LeNet 系列架構，并為 MNIST 和 CIFAR 數據集創建，訓練和評估了 LeNet 族模型。 TensorFlow 和 Keras 提供了許多卷積和池化層和操作。鼓勵讀者探索本章未涉及的層和操作。 在下一章中，我們將繼續學習如何使用自編碼器架構將 TensorFlow 應用于圖像數據。