### 3.2整改 多層網絡通常是高度非線性的，并且整流通常是將非線性引入模型的第一階段處理。整流是指將點狀非線性（也稱為激活函數）應用于卷積層的輸出。該術語的使用借鑒了信號處理，其中整流是指從交流到直流的轉換。這是另一個處理步驟，從生物學和理論點觀點中找到動機。計算神經科學家引入整流步驟，以尋找最佳解釋手頭神經科學數據的適當模型。另一方面，機器學習研究人員使用整改來獲得學習更快更好的模型。有趣的是，兩個研究流程都傾向于同意，不僅僅是需要糾正，而且它們也趨同于同一類型的整改。 #### 3.2.1生物學觀點 從生物學的角度來看，整流非線性通常被引入到神經元的計算模型中，以便解釋它們作為輸入函數的激發率[31]。生物神經元的射擊率一般被廣泛接受的模型被稱為漏泄積分和火（LIF）[31]。該模型解釋了任何神經元的輸入信號必須超過某個閾值才能使細胞發射。研究視皮層細胞的研究也特別依賴于類似的模型，稱為半波整流[74,109,66]。 值得注意的是，Hubel和Wiesel的開創性工作已經證明，簡單單元包括線性濾波后半波整流的非線性處理[74]。如前面3.1節所述，線性算子本身可以被認為是卷積運算。眾所周知，根據輸入信號，卷積可以產生正或負輸出。然而，實際上細胞的“放電速率是定義為正。這就是為什么Hubel和Wiesel建議采用剪切操作形式的非線性，只考慮正反應。更符合LIF模型，其他研究建議略有不同的半波整流，其中削波操作基于某個閾值（_即_。除了零之外）[109]。另一個更完整的模型也考慮了可能出現的負面反應在這種情況下，作者提出了一種雙路半波整流方法，其中正負輸入信號分別被截斷并在兩條不同的路徑中傳輸。另外，為了處理負數響應兩個信號之后是逐點平方操作，因此整流被稱為半平方（雖然生物神經元不一定共享這個屬性）。在這個mo del將細胞視為編碼正負輸出的相反相的能量機制。 ##### 討論 值得注意的是，這些具有生物學動機的神經元激活功能模型已成為當今卷積網絡算法的常見做法，并且部分地對其成功的大部分負責，這將在下面討論。 #### 3.2.2理論觀點 從理論的角度來看，機械學習研究人員通常會引入整改，主要有兩個原因。首先，它通過允許網絡學習更復雜的功能來用于增加提取的特征的區分能力。其次，它允許控制數據的數字表示以便更快地學習。歷史上，多層網絡依賴于使用邏輯非線性或雙曲正切的逐點S形非線性[91]。雖然邏輯函數在生物學上更合理，因為它沒有負輸出，但更常使用雙曲正切，因為它具有更好的學習性質，例如周圍的穩態（見圖3.7（a）和（b），分別）。為了說明雙曲正切激活函數的負部分，通常后面是模數運算（也稱為絕對值整流AVR）[77]。然而，最近由Nair _等_首次引入的整流線性單元（ReLU）。 [111]，很快成為許多領域的默認整流非線性（_，例如_。[103]），尤其是計算機視覺以來，它首次成功應用于ImageNet數據集[88]。在[88]中顯示，與傳統的S形整流功能相比，ReLU在過度擬合和加速訓練過程中起著關鍵作用，即使在導致更好的性能的同時也是如此。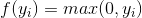 數學上，ReLU定義如下， （3.2） 并在圖3.7（c）中描述。對于任何基于學習的網絡，ReLU運營商有兩個主要的理想屬性。首先，由于正輸入的導數為，因此ReLU不會對正輸入飽和。這種特性使得ReLU特別具有吸引力，因為它消除了依賴于S形非線性的網絡中通常存在的消失梯度的問題。其次，鑒于當輸入為負時，ReLU將輸出設置為，它引入了稀疏性，這有利于更快的訓練和更好的分類準確性。實際上，為了改進分類，通常希望具有線性可分的特征，稀疏表示通常更容易分離[54]。然而，負輸入的硬飽和度具有其自身的風險。這里有兩個互補的問題。首先，由于硬零點激活，如果從未激活到這些部分的路徑，則網絡的某些部分可能永遠不會被訓練。其次，在退化的情況下，給定層的所有單元都有負輸入，反向傳播可能會失敗，這將導致類似消失梯度問題的情況。由于這些潛在的問題，已經提出了對ReLU非線性的許多改進以更好地處理負輸出的情況，同時保持ReLU的優點。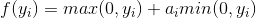 ReLU激活函數的變化包括漏泄整流線性單元（LReLU）[103]及其密切相關的參數整流線性單元（PReLU）[63]，它們在數學上被定義為 （3.3） 并在圖3.7（d）中描述。在LRelu中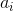是固定值，而在PReLU中學習。最初引入LReLU是為了避免反向傳播期間的零梯度，但沒有顯著改善測試網絡的結果。此外，它在選擇參數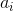時嚴重依賴交叉驗證實驗。相比之下，PReLU在訓練期間優化了該參數的值，從而提高了性能。值得注意的是，PReLU最重要的結果之一是網絡中的早期層傾向于學習更高的參數值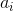，而對于網絡層次結構中的更高層，該數字幾乎可以忽略不計。作者推測這個結果可能是由于在不同層次學習過濾器的性質。特別是，由于第一層內核通常是帶狀濾波器，所以響應的兩個部分都保持不變，因為它們代表輸入信號的潛在顯著差異。另一方面，更高層的內核被調整為檢測特定對象并且被訓練為更加不變。 | 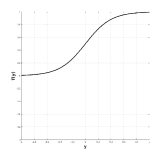 | 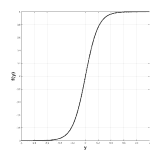 | 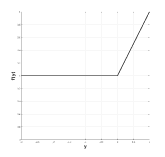 | | （a）物流 | （b）tanh | （c）ReLU | | 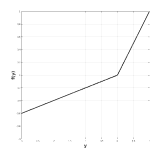 | 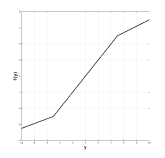 | 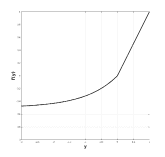 | | （d）LReLU / PReLU | （e）SReLU | （f）EReLU | 圖3.7：多層網絡文獻中使用的非線性校正函數。 有趣的是，基于類似的觀察[132]提出了另一種整流功能，稱為級聯整流線性單元（CReLU）。在這種情況下，作者建議CReLU從觀察開始，在大多數ConvNets的初始層學習的內核傾向于形成負相關對（_即_。過濾器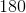度異相）如圖所示在圖3.8中。這一觀察意味著ReLU非線性消除的負響應被相反相位的學習核所取代。通過用CReLU替換ReLU，作者能夠證明設計用于編碼雙路徑校正的網絡可以帶來更好的性能，同時通過消除冗余來減少要學習的參數數量。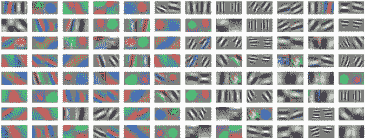  圖3.8：由ImageNet數據集訓練的AlexNet學習的Conv1過濾器的可視化。圖[132]轉載。 ReLU系列的其他變化包括：S形整流線性單元（SReLU）[82]，定義為 （3.4） 并在圖3.7（e）中描述，其被引入以允許網絡學習更多的非線性變換。它由三個分段線性函數和4個可學習參數組成。 SReLU的主要缺點是它引入了幾個要學習的參數（_，即_。特別是如果參數不在多個通道之間共享），這使得學習變得更加復雜。考慮到這些參數的錯誤初始化可能會損害學習，這種擔憂尤其如此。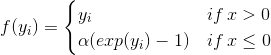另一種變體是指數線性單位（ELU）[26]，定義為 （3.5） 并且如圖3.7（f）所示，其動機是希望通過迫使信號飽和到由負輸入的變量控制的值來增加噪聲的不變性。 ReLU家族中所有變體的共同點是，也應該考慮負面輸入并進行適當處理。 在散射網絡[15]中提出了對整流非線性選擇的另一種展望。如前面3.1節所述，ScatNet是手工制作的，其主要目標是增加表示對各種變換的不變性。由于它在卷積層中廣泛依賴于小波，因此它對于小的變形是不變的;但是，它仍然適用于翻譯。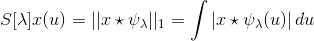因此，作者依賴于定義為的積分運算 （3.6） 并實現為平均合并，以增加移位不變性水平。因此，預期隨后的匯集操作可以將響應推向零，_即_。在正響應和負響應相互抵消的情況下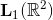，范數運算符用于整流步驟以使所有響應為正。再一次，值得注意的是，依賴于雙曲正切激活函數的傳統ConvNets也使用類似的AVR校正來處理負輸出[91,77]。此外，更多生物學動機模型，如半平方整流[66,67]，依賴于信號的逐點平方來處理負響應。該平方操作還允許在能量機制方面對響應進行推理。有趣的是，最近一個理論驅動的卷積網絡[60]也提出了一個定義為兩路徑整流策略 （3.7） 其中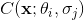是卷積運算的輸出。該整流策略結合了保持濾波信號的兩個相位和逐點平方的思想，從而允許在考慮光譜能量方面的結果信號的同時保護信號幅度和相位。 ##### Discussion 有趣的是，從理論的角度來看，廣泛的ReLU非線性明顯成為整流階段最受歡迎的選擇。值得注意的是，完全忽略負輸入（_即_。在ReLU中所做的）的選擇似乎更值得懷疑，因為提出替代選擇的許多貢獻證明了這一點[103,63,82,26,132] ]。將ReLU的行為與ScatNet [15]和舊的ConvNet架構[77]中使用的AVR校正進行比較也很重要。雖然AVR保留了能量信息但是擦除了相位信息，但另一方面，ReLU通過僅保留信號的正部分來保持某種意義上的相位信息;然而，它不會保留能量，因為它會丟棄一半的信號。值得注意的是，嘗試保留兩者的方法（_，例如_ .CReLU [132]和在SOE-Net [60]中使用（3.7））能夠在多個任務中獲得更好的性能，并且這些方法是也與生物學研究結果一致[66]。