八、自編碼器 · ApacheCN 深度學習譯文集

# 八、自編碼器自編碼器是前饋，非循環神經網絡，可通過無監督學習來學習。他們具有學習數據的緊湊表示的固有能力。它們是深度信念網絡的中心，可在圖像重建，聚類，機器翻譯等領域找到應用。在本章中，您將學習和實現自編碼器的不同變體，并最終學習如何堆疊自編碼器。本章包括以下主題： * 普通自編碼器 * 稀疏自編碼器 * 去噪自編碼器 * 卷積自編碼器 * 棧式自編碼器 # 介紹自編碼器，也稱為**空竹網絡**或**自動關聯器**，最初由 Hinton 和 PDP 小組于 1980 年代提出。它們是前饋網絡，沒有任何反饋，并且它們是通過無監督學習來學習的。像第 3 章的多人感知機，神經網絡感知機一樣，它們使用反向傳播算法進行學習，但有一個主要區別-目標與輸入相同。我們可以認為自編碼器由兩個級聯網絡組成-第一個網絡是編碼器，它接受輸入`x`，然后使用變換`h`將其編碼為編碼信號`y`： `y = h(x)` 第二網絡使用編碼信號`y`作為其輸入，并執行另一個變換`f`以獲得重構信號`r`： `r = f(y) = f(h(x))` 我們將誤差`e`定義為原始輸入`x`與重構信號`r`之間的差，`e = x - r`。然后，網絡通過減少**均方誤差**（**MSE**）進行學習，并且像 MLP 一樣，該誤差會傳播回隱藏層。下圖顯示了自編碼器，其中編碼器和解碼器分別突出顯示。自編碼器可以具有權重分配，也就是說，解碼器和編碼器的權重只是彼此的換位，這可以在訓練參數數量較少時幫助網絡更快地學習，但同時會降低編碼器的自由度。網絡。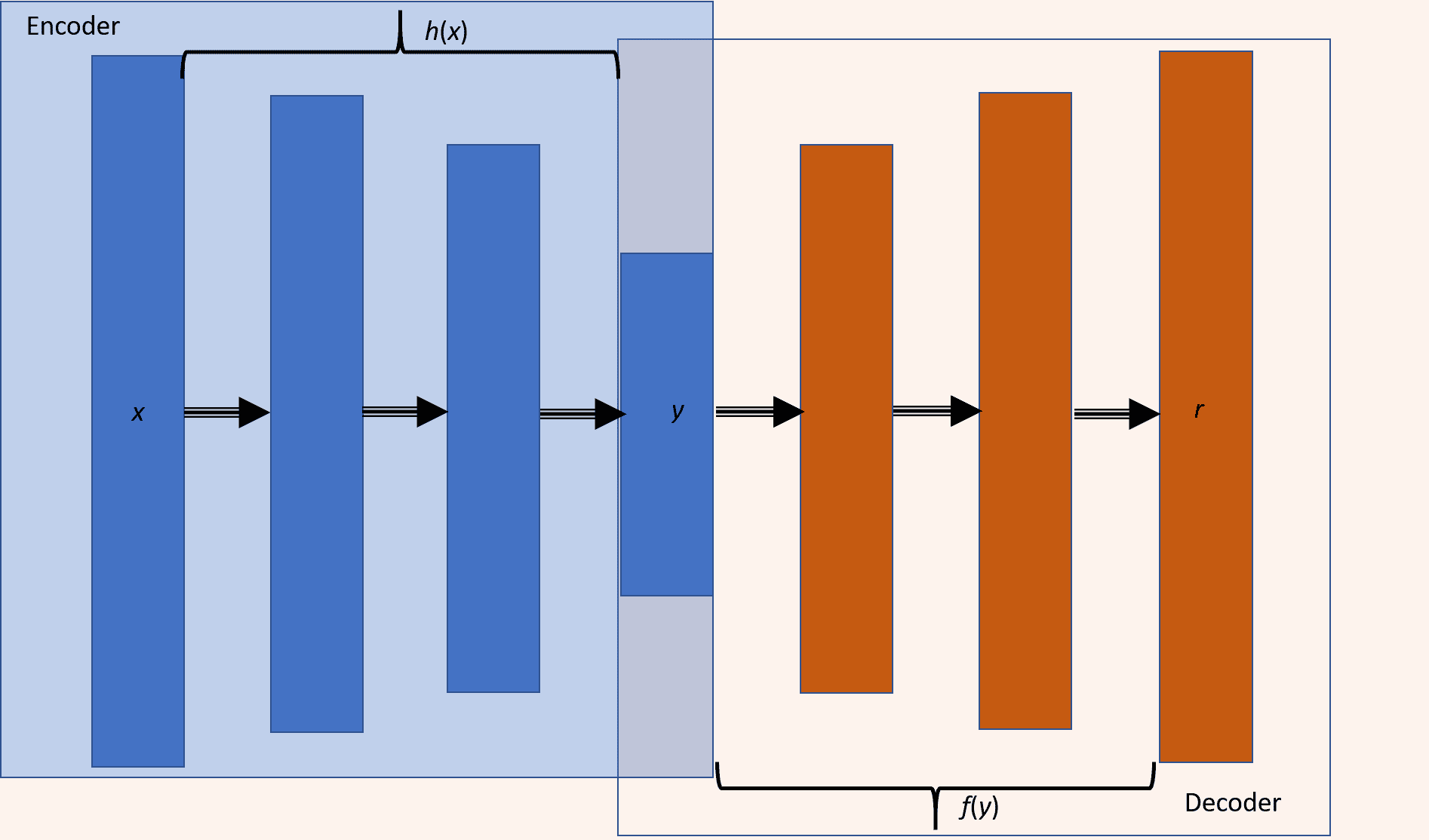它們與第 7 章“無監督學習”的 RBM 非常相似，但有一個很大的區別-自編碼器中神經元的狀態是確定性的，而在 RBM 中，神經元是概率性的： ![](https://img.kancloud.cn/f8/b3/f8b3360b3c48044b7783ab5aedf72732_1894x1114.png) 根據隱藏層的大小，自編碼器分為**不完整**（隱藏層的神經元少于輸入層）或**過完整**（隱藏層的神經元多于輸入層）。。根據對損失施加的限制/約束，我們有多種類型的自編碼器：稀疏自編碼器，降噪自編碼器和卷積自編碼器。在本章中，您將了解自編碼器中的這些變體，并使用 TensorFlow 實現它們。自編碼器的明顯應用之一是在降維領域[2]。結果表明，與 PCA 相比，自編碼器產生了更好的結果。自編碼器還可以用于特征提取[3]，文檔檢索[2]，分類和異常檢測。 # 另見 * `Rumelhart, David E., Geoffrey E. Hinton, and Ronald J. Williams. Learning internal representations by error propagation. No. ICS-8506. California Univ San Diego La Jolla Inst for Cognitive Science, 1985. (http://www.cs.toronto.edu/~fritz/absps/pdp8.pdf)` * `Hinton, Geoffrey E., and Ruslan R. Salakhutdinov. Reducing the dimensionality of data with neural networks, science 313.5786 (2006): 504-507. (https://pdfs.semanticscholar.org/7d76/b71b700846901ac4ac119403aa737a285e36.pdf)` * `Masci, Jonathan, et al. Stacked convolutional auto-encoders for hierarchical feature extraction. Artificial Neural Networks and Machine Learning–ICANN 2011 (2011): 52-59. (https://www.researchgate.net/profile/Jonathan_Masci/publication/221078713_Stacked_Convolutional_Auto-Encoders_for_Hierarchical_Feature_Extraction/links/0deec518b9c6ed4634000000/Stacked-Convolutional-Auto-Encoders-for-Hierarchical-Feature-Extraction.pdf)` * `Japkowicz, Nathalie, Catherine Myers, and Mark Gluck. A novelty detection approach to classification. IJCAI. Vol. 1. 1995. (http://www.ijcai.org/Proceedings/95-1/Papers/068.pdf)` # 普通自編碼器 Hinton 提出的普通自編碼器僅包含一個隱藏層。隱藏層中神經元的數量少于輸入（或輸出）層中神經元的數量。這導致對網絡中信息流產生瓶頸效應，因此我們可以將隱藏層視為瓶頸層，從而限制了要存儲的信息。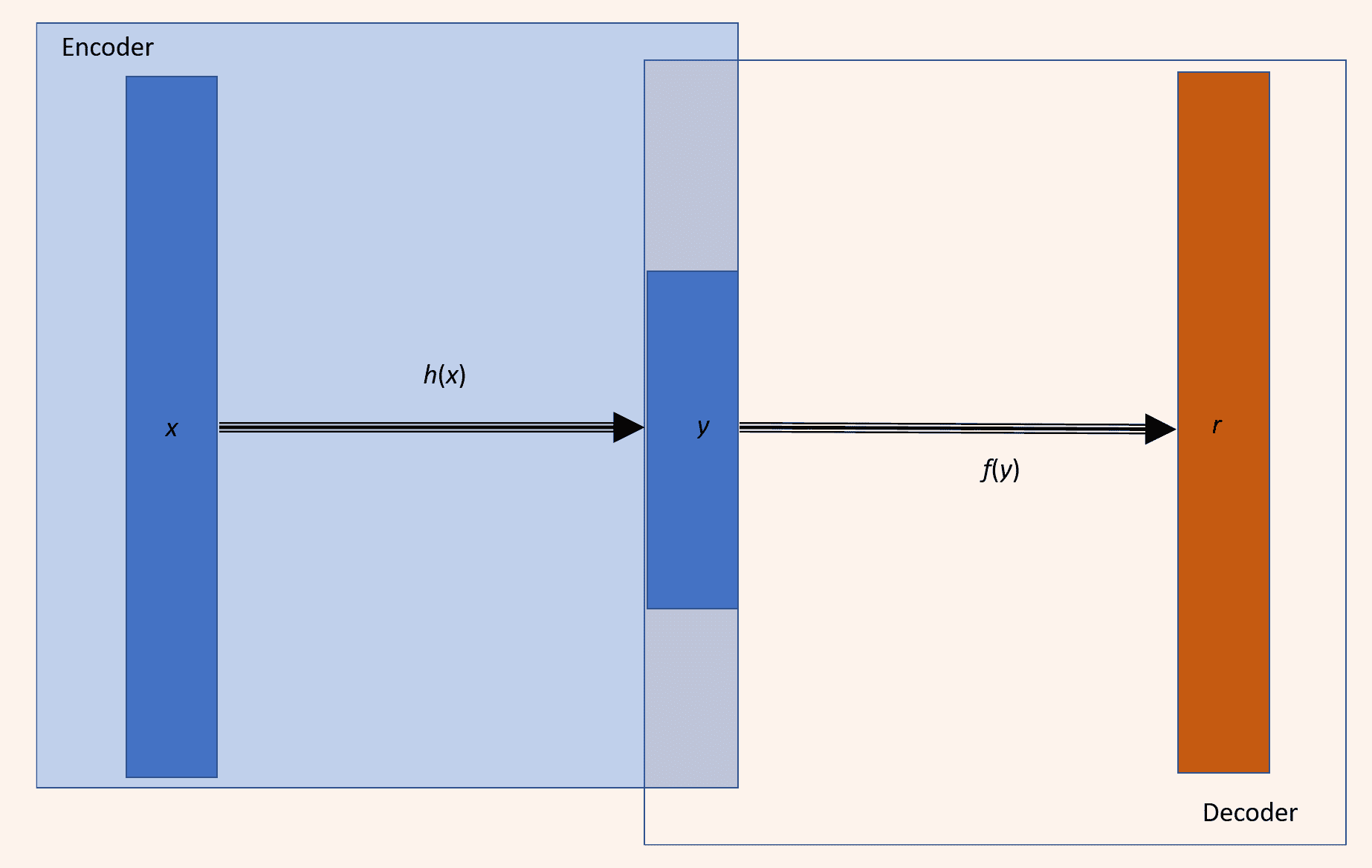自編碼器中的學習包括在隱藏層上開發輸入信號的緊湊表示，以便輸出層可以忠實地再現原始輸入： ![](https://img.kancloud.cn/4f/0e/4f0ef4ba14ee90d284596bbe8350074d_1846x1168.png) 具有單個隱藏層的自編碼器 # 準備此秘籍將使用自編碼器進行圖像重建；我們將在 MNIST 數據庫上訓練自編碼器，并將其用于重建測試圖像。 # 操作步驟我們按以下步驟進行： 1. 與往常一樣，第一步是導入所有必需的模塊： ```py import tensorflow as tf import numpy as np from tensorflow.examples.tutorials.mnist import input_data import matplotlib.pyplot as plt %matplotlib inline ``` 2. 接下來，我們從 TensorFlow 示例中獲取 MNIST 數據-這里要注意的重要一點是，標簽不是一次性編碼的，僅僅是因為我們沒有使用標簽來訓練網絡。自編碼器通過無監督學習來學習： ```py mnist = input_data.read_data_sets("MNIST_data/") trX, trY, teX, teY = mnist.train.images, mnist.train.labels, mnist.test.images, mnist.test.labels ``` 3. 接下來，我們聲明一個類`AutoEncoder`；該類具有`init`方法來為自編碼器初始化權重，偏差和占位符。我們還可以使用`init`方法構建完整的圖。該類還具有用于`encoder`，`decoder`，設置會話（`set_session`）和`fit`的方法。我們在此處構建的自編碼器使用簡單的 MSE 作為`loss`函數，我們嘗試使用`AdamOptimizer`對其進行優化： ```py class AutoEncoder(object): def __init__(self, m, n, eta = 0.01): """ m: Number of neurons in input/output layer n: number of neurons in hidden layer """ self._m = m self._n = n self.learning_rate = eta # Create the Computational graph # Weights and biases self._W1 = tf.Variable(tf.random_normal(shape=(self._m,self._n))) self._W2 = tf.Variable(tf.random_normal(shape=(self._n,self._m))) self._b1 = tf.Variable(np.zeros(self._n).astype(np.float32)) #bias for hidden layer self._b2 = tf.Variable(np.zeros(self._m).astype(np.float32)) #bias for output layer # Placeholder for inputs self._X = tf.placeholder('float', [None, self._m]) self.y = self.encoder(self._X) self.r = self.decoder(self.y) error = self._X - self.r self._loss = tf.reduce_mean(tf.pow(error, 2)) self._opt = tf.train.AdamOptimizer(self.learning_rate).minimize(self._loss) def encoder(self, x): h = tf.matmul(x, self._W1) + self._b1 return tf.nn.sigmoid(h) def decoder(self, x): h = tf.matmul(x, self._W2) + self._b2 return tf.nn.sigmoid(h) def set_session(self, session): self.session = session def reduced_dimension(self, x): h = self.encoder(x) return self.session.run(h, feed_dict={self._X: x}) def reconstruct(self,x): h = self.encoder(x) r = self.decoder(h) return self.session.run(r, feed_dict={self._X: x}) def fit(self, X, epochs = 1, batch_size = 100): N, D = X.shape num_batches = N // batch_size obj = [] for i in range(epochs): #X = shuffle(X) for j in range(num_batches): batch = X[j * batch_size: (j * batch_size + batch_size)] _, ob = self.session.run([self._opt,self._loss], feed_dict={self._X: batch}) if j % 100 == 0 and i % 100 == 0: print('training epoch {0} batch {2} cost {1}'.format(i,ob, j)) obj.append(ob) return obj ``` 為了能夠在訓練后使用自編碼器，我們還定義了兩個工具函數：`reduced_dimension`提供編碼器網絡的輸出，`reconstruct`重構最終圖像。 4. 我們將輸入數據轉換為`float`進行訓練，初始化所有變量，然后開始計算會話。在計算中，我們目前僅測試自編碼器的重構能力： ```py Xtrain = trX.astype(np.float32) Xtest = teX.astype(np.float32) _, m = Xtrain.shape autoEncoder = AutoEncoder(m, 256) #Initialize all variables init = tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) autoEncoder.set_session(sess) err = autoEncoder.fit(Xtrain, epochs=10) out = autoEncoder.reconstruct(Xtest[0:100]) ``` 5. 我們可以通過繪制誤差與周期的關系圖來驗證我們的網絡在訓練時是否確實優化了 MSE。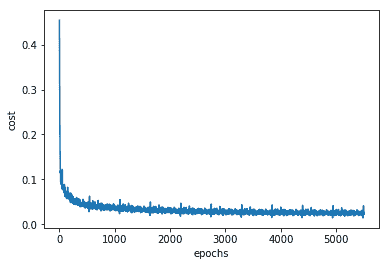為了獲得良好的訓練，應該使用`epochs`來減少誤差： ```py plt.plot(err) plt.xlabel('epochs') plt.ylabel('cost') ``` 該圖如下所示： ![](https://img.kancloud.cn/0d/9c/0d9ca56559e95437478e9d388700eb6a_389x266.png) 我們可以看到，隨著網絡的學習，損耗/成本正在降低，到我們達到 5,000 個周期時，損耗/成本幾乎在一條線上振蕩。這意味著進一步增加周期將是無用的。如果現在要改善訓練，則應該更改超參數，例如學習率，批量大小和使用的優化程序。 6. 現在讓我們看一下重建的圖像。在這里，您可以同時看到由我們的自編碼器生成的原始圖像和重建圖像： ```py # Plotting original and reconstructed images row, col = 2, 8 idx = np.random.randint(0, 100, row * col // 2) f, axarr = plt.subplots(row, col, sharex=True, sharey=True, figsize=(20,4)) for fig, row in zip([Xtest,out], axarr): for i,ax in zip(idx,row): ax.imshow(fig[i].reshape((28, 28)), cmap='Greys_r') ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) ``` 我們得到以下結果： ![](https://img.kancloud.cn/93/16/931688da65303d5d8dd78fa1074db0cc_1137x238.png) # 工作原理有趣的是，在前面的代碼中，我們將輸入的尺寸從 784 減少到 256，并且我們的網絡仍可以重建原始圖像。讓我們比較一下具有相同隱藏層尺寸的 RBM（第 7 章，無監督學習）的表現： ![](https://img.kancloud.cn/e4/90/e49009394f3940ae54c9845288a6ff9c_1411x965.png) 我們可以看到，自編碼器重建的圖像比 RBM 重建的圖像更清晰。原因是，在自編碼器中，還有其他權重（從隱藏層到解碼器輸出層的權重）需要訓練，因此保留了學習知識。隨著自編碼器了解更多，即使兩者都將信息壓縮到相同的尺寸，它的表現也比 RBM 更好。 # 更多諸如 PCA 之類的自編碼器可以用于降維，但是 PCA 僅可以表示線性變換，但是我們可以在自編碼器中使用非線性激活函數，從而在編碼中引入非線性。這是從 Hinton 論文復制的結果，該結果使用*神經網絡*降低了數據的維數。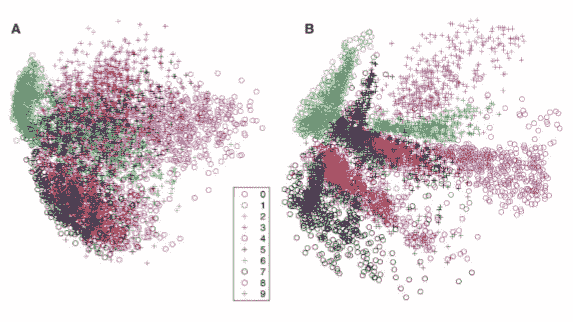該結果將 PCA（A）的結果與棧式 RBM 作為具有 784-1000-500-250-2 架構的自編碼器的結果進行了比較： ![](https://img.kancloud.cn/2c/28/2c28098a3e8ae7bdf4508e3d86c5e9da_573x322.png) 正如我們稍后將看到的，當使用棧式自編碼器制作自編碼器時，每個自編碼器最初都經過單獨的預訓練，然后對整個網絡進行微調以獲得更好的表現。 # 稀疏自編碼器我們在前面的秘籍中看到的自編碼器的工作方式更像是一個身份網絡-它們只是重構輸入。重點是在像素級別重建圖像，唯一的限制是瓶頸層中的單元數；有趣的是，像素級重建不能確保網絡將從數據集中學習抽象特征。通過添加更多約束，我們可以確保網絡從數據集中學習抽象特征。在稀疏自編碼器中，將稀疏懲罰項添加到重構誤差中，以確保在任何給定時間觸發瓶頸層中較少的單元。如果`m`是輸入模式的總數，那么我們可以定義一個數量`ρ_hat`（您可以在 [Andrew Ng 的講座](https://web.stanford.edu/class/cs294a/sparseAutoencoder_2011new.pdf)中檢查數學細節），它測量每個隱藏層單元的凈活動（平均觸發多少次）。基本思想是放置一個約束`ρ_hat`，使其等于稀疏性參數`ρ`。這導致損失函數中添加了稀疏性的正則項，因此現在`loss`函數如下： ```py loss = Mean squared error + Regularization for sparsity parameter ``` 如果`ρ_hat`偏離`ρ`，則此正則化項將對網絡造成不利影響；做到這一點的一種標準方法是使用`ρ`和`ρ_hat`之間的 **Kullback-Leiber** （**KL**）差異。 # 準備在開始秘籍之前，讓我們進一步探討 KL 的差異，`D[KL]`。它是兩個分布之間差異的非對稱度量，在我們的情況下為`ρ`和`ρ_hat`。當`ρ`和`ρ_hat`相等時，則為零，否則，當`ρ_hat`與`ρ`分叉時，它單調增加。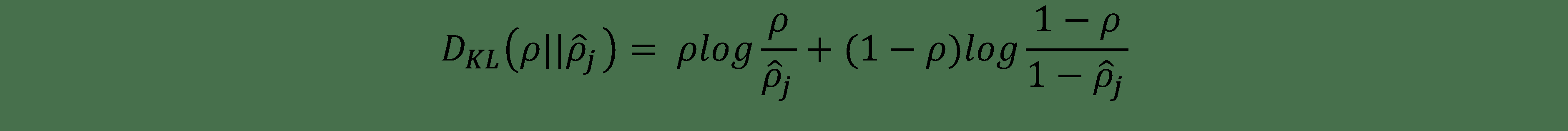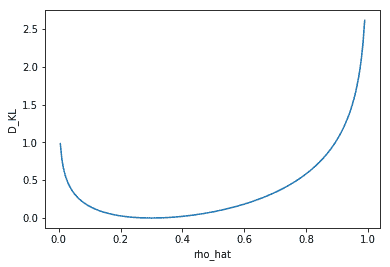在數學上，它表示為： ![](https://img.kancloud.cn/67/2c/672c6d34964f40372c142fdd093a9514_3760x314.png) 這是固定`ρ = 0.3`時`D[KL]`的圖，我們可以看到當`ρ_hat = 0.3`時，`D[KL] = 0`；否則在兩端單調增長： ![](https://img.kancloud.cn/ed/ea/edea300e83e38a7d6091b11381b9a45a_390x267.png) # 操作步驟我們按以下步驟進行： 1. 我們導入必要的模塊： ```py import tensorflow as tf import numpy as np from tensorflow.examples.tutorials.mnist import input_data import matplotlib.pyplot as plt %matplotlib inline ``` 2. 從 TensorFlow 示例中加載 MNIST 數據集： ```py mnist = input_data.read_data_sets("MNIST_data/") trX, trY, teX, teY = mnist.train.images, mnist.train.labels, mnist.test.images, mnist.test.labels ``` 3. 定義`SparseAutoEncoder`類，它與前面的秘籍中的`AutoEncoder`類非常相似，除了引入了 KL 散度損失之外： ```py def kl_div(self, rho, rho_hat): term2_num = tf.constant(1.)- rho term2_den = tf.constant(1.) - rho_hat kl = self.logfunc(rho,rho_hat) + self.logfunc(term2_num, term2_den) return kl def logfunc(self, x1, x2): return tf.multiply( x1, tf.log(tf.div(x1,x2))) ``` 我們將 KL 約束添加到損失中，如下所示： ```py alpha = 7.5e-5 kl_div_loss = tf.reduce_sum(self.kl_div(0.02, tf.reduce_mean(self.y,0))) loss = self._loss + alpha * kl_div_loss ``` 在此，`alpha`是賦予稀疏性約束的權重。該類的完整代碼如下： ```py class SparseAutoEncoder(object): def __init__(self, m, n, eta = 0.01): """ m: Number of neurons in input/output layer n: number of neurons in hidden layer """ self._m = m self._n = n self.learning_rate = eta # Create the Computational graph # Weights and biases self._W1 = tf.Variable(tf.random_normal(shape=(self._m,self._n))) self._W2 = tf.Variable(tf.random_normal(shape=(self._n,self._m))) self._b1 = tf.Variable(np.zeros(self._n).astype(np.float32)) #bias for hidden layer self._b2 = tf.Variable(np.zeros(self._m).astype(np.float32)) #bias for output layer # Placeholder for inputs self._X = tf.placeholder('float', [None, self._m]) self.y = self.encoder(self._X) self.r = self.decoder(self.y) error = self._X - self.r self._loss = tf.reduce_mean(tf.pow(error, 2)) alpha = 7.5e-5 kl_div_loss = tf.reduce_sum(self.kl_div(0.02, tf.reduce_mean(self.y,0))) loss = self._loss + alpha * kl_div_loss self._opt = tf.train.AdamOptimizer(self.learning_rate).minimize(loss) def encoder(self, x): h = tf.matmul(x, self._W1) + self._b1 return tf.nn.sigmoid(h) def decoder(self, x): h = tf.matmul(x, self._W2) + self._b2 return tf.nn.sigmoid(h) def set_session(self, session): self.session = session def reduced_dimension(self, x): h = self.encoder(x) return self.session.run(h, feed_dict={self._X: x}) def reconstruct(self,x): h = self.encoder(x) r = self.decoder(h) return self.session.run(r, feed_dict={self._X: x}) def kl_div(self, rho, rho_hat): term2_num = tf.constant(1.)- rho term2_den = tf.constant(1.) - rho_hat kl = self.logfunc(rho,rho_hat) + self.logfunc(term2_num, term2_den) return kl def logfunc(self, x1, x2): return tf.multiply( x1, tf.log(tf.div(x1,x2))) def fit(self, X, epochs = 1, batch_size = 100): N, D = X.shape num_batches = N // batch_size obj = [] for i in range(epochs): #X = shuffle(X) for j in range(num_batches): batch = X[j * batch_size: (j * batch_size + batch_size)] _, ob = self.session.run([self._opt,self._loss], feed_dict={self._X: batch}) if j % 100 == 0: print('training epoch {0} batch {2} cost {1}'.format(i,ob, j)) obj.append(ob) return obj ``` 4. 接下來，我們聲明`SparseAutoEncoder`類的對象，對訓練數據進行擬合，并計算重建的圖像： ```py Xtrain = trX.astype(np.float32) Xtest = teX.astype(np.float32) _, m = Xtrain.shape sae = SparseAutoEncoder(m, 256) #Initialize all variables init = tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) sae.set_session(sess) err = sae.fit(Xtrain, epochs=10) out = sae.reconstruct(Xtest[0:100]) ``` 5. 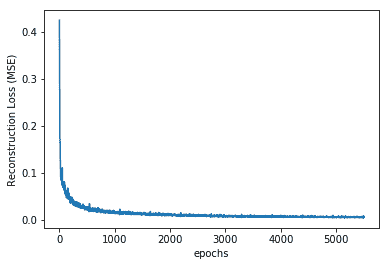讓我們看看隨著網絡學習，均方重構損失的變化： ```py plt.plot(err) plt.xlabel('epochs') plt.ylabel('Reconstruction Loss (MSE)') ``` 情節如下： ![](https://img.kancloud.cn/2e/83/2e83dd6b79eba116b4aee824b648325e_389x266.png) 6. 讓我們看一下重建的圖像： ```py # Plotting original and reconstructed images row, col = 2, 8 idx = np.random.randint(0, 100, row * col // 2) f, axarr = plt.subplots(row, col, sharex=True, sharey=True, figsize=(20,4)) for fig, row in zip([Xtest,out], axarr): for i,ax in zip(idx,row): ax.imshow(fig[i].reshape((28, 28)), cmap='Greys_r') ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) ``` 我們得到以下結果： ![](https://img.kancloud.cn/91/88/91886cc3be27f081b798f6f0fe5516e7_1137x238.png) # 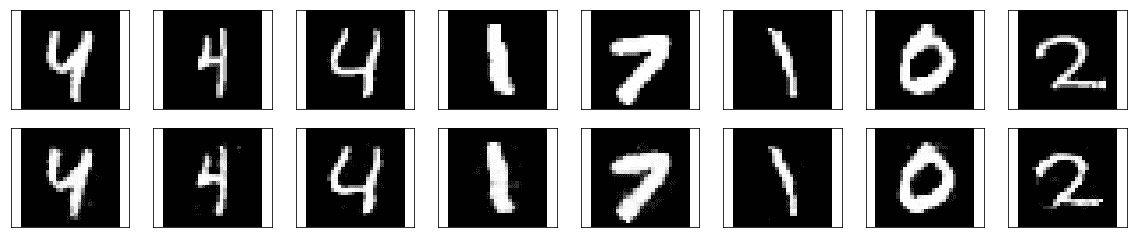工作原理您必須已經注意到，稀疏自編碼器的主要代碼與普通自編碼器的主要代碼完全相同，這是因為稀疏自編碼器只有一個主要變化-增加了 KL 發散損耗以確保稀疏性。隱藏的（瓶頸）層。但是，如果比較這兩個重構，則可以發現即使在隱藏層中具有相同數量的單元，稀疏自編碼器也比標準編碼器好得多： ![](https://img.kancloud.cn/c9/d1/c9d17888e24984de49f9b3b06f01986b_1416x944.png) 訓練 MNIST 數據集的原始自編碼器后的重建損失為 0.022，而稀疏自編碼器則為 0.006。因此，添加約束會迫使網絡學習數據的隱藏表示。 # 更多輸入的緊湊表示形式以權重存儲；讓我們可視化網絡學習到的權重。這分別是標準自編碼器和稀疏自編碼器的編碼器層的權重。我們可以看到，在標準自編碼器中，許多隱藏單元的權重非常大，表明它們工作過度： ![](https://img.kancloud.cn/57/b7/57b7312726e7267370a47ffc15d4d718_1757x1007.png) # 另見 * <http://web.engr.illinois.edu/~hanj/cs412/bk3/KL-divergence.pdf> * <https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence> # 去噪自編碼器我們在前兩個秘籍中探討過的兩個自編碼器是**未完成的**自編碼器的示例，因為與輸入（輸出）層相比，它們中的隱藏層具有較低的尺寸。去噪自編碼器屬于**過完整**自編碼器的類別，因為當隱藏層的尺寸大于輸入層的尺寸時，它會更好地工作。去噪自編碼器從損壞的（嘈雜的）輸入中學習；它為編碼器網絡提供噪聲輸入，然后將來自解碼器的重建圖像與原始輸入進行比較。這個想法是，這將幫助網絡學習如何去噪輸入。它不再只是按像素進行比較，而是為了進行去噪，還將學習相鄰像素的信息。 # 準備去噪自編碼器還將具有 KL 散度懲罰項；它在兩個主要方面與先前秘籍的稀疏自編碼器有所不同。首先，`n_hidden > m`瓶頸層中的隱藏單元數大于輸入層`m`中的單元數`n_hidden > m`。其次，編碼器的輸入已損壞。為了在 TensorFlow 中做到這一點，我們添加了`invalid`函數，這給輸入增加了噪音： ```py def corruption(x, noise_factor = 0.3): #corruption of the input noisy_imgs = x + noise_factor * np.random.randn(*x.shape) noisy_imgs = np.clip(noisy_imgs, 0., 1.) return noisy_imgs ``` # 操作步驟 1. 像往常一樣，第一步是導入必要的模塊-TensorFlow，numpy 來操縱輸入數據，matplotlib 來進行繪制，等等： ```py import tensorflow as tf import numpy as np from tensorflow.examples.tutorials.mnist import input_data import matplotlib.pyplot as plt import math %matplotlib inline ``` 2. 從 TensorFlow 示例中加載數據。在本章的所有秘籍中，我們都使用標準的 MNIST 數據庫進行說明，以便為您提供不同自編碼器之間的基準。 ```py mnist = input_data.read_data_sets("MNIST_data/") trX, trY, teX, teY = mnist.train.images, mnist.train.labels, mnist.test.images, mnist.test.labels ``` 3. 接下來，我們定義此秘籍的主要組成部分`DenoisingAutoEncoder`類。該類與我們在前面的秘籍中創建的`SparseAutoEncoder`類非常相似。在這里，我們為噪點圖像添加了一個占位符；該噪聲輸入被饋送到編碼器。現在，當輸入的是噪點圖像時，重構誤差就是原始清晰圖像與解碼器輸出之間的差。我們在此保留稀疏懲罰條款。因此，擬合函數將原始圖像和噪聲圖像都作為其參數。 ```py class DenoisingAutoEncoder(object): def __init__(self, m, n, eta = 0.01): """ m: Number of neurons in input/output layer n: number of neurons in hidden layer """ self._m = m self._n = n self.learning_rate = eta # Create the Computational graph # Weights and biases self._W1 = tf.Variable(tf.random_normal(shape=(self._m,self._n))) self._W2 = tf.Variable(tf.random_normal(shape=(self._n,self._m))) self._b1 = tf.Variable(np.zeros(self._n).astype(np.float32)) #bias for hidden layer self._b2 = tf.Variable(np.zeros(self._m).astype(np.float32)) #bias for output layer # Placeholder for inputs self._X = tf.placeholder('float', [None, self._m]) self._X_noisy = tf.placeholder('float', [None, self._m]) self.y = self.encoder(self._X_noisy) self.r = self.decoder(self.y) error = self._X - self.r self._loss = tf.reduce_mean(tf.pow(error, 2)) #self._loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(labels =self._X, logits = self.r)) alpha = 0.05 kl_div_loss = tf.reduce_sum(self.kl_div(0.02, tf.reduce_mean(self.y,0))) loss = self._loss + alpha * kl_div_loss self._opt = tf.train.AdamOptimizer(self.learning_rate).minimize(loss) def encoder(self, x): h = tf.matmul(x, self._W1) + self._b1 return tf.nn.sigmoid(h) def decoder(self, x): h = tf.matmul(x, self._W2) + self._b2 return tf.nn.sigmoid(h) def set_session(self, session): self.session = session def reconstruct(self,x): h = self.encoder(x) r = self.decoder(h) return self.session.run(r, feed_dict={self._X: x}) def kl_div(self, rho, rho_hat): term2_num = tf.constant(1.)- rho term2_den = tf.constant(1.) - rho_hat kl = self.logfunc(rho,rho_hat) + self.logfunc(term2_num, term2_den) return kl def logfunc(self, x1, x2): return tf.multiply( x1, tf.log(tf.div(x1,x2))) def corrupt(self,x): return x * tf.cast(tf.random_uniform(shape=tf.shape(x), minval=0,maxval=2),tf.float32) def getWeights(self): return self.session.run([self._W1, self._W2,self._b1, self._b2]) def fit(self, X, Xorg, epochs = 1, batch_size = 100): N, D = X.shape num_batches = N // batch_size obj = [] for i in range(epochs): #X = shuffle(X) for j in range(num_batches): batch = X[j * batch_size: (j * batch_size + batch_size)] batchO = Xorg[j * batch_size: (j * batch_size + batch_size)] _, ob = self.session.run([self._opt,self._loss], feed_dict={self._X: batchO, self._X_noisy: batch}) if j % 100 == 0: print('training epoch {0} batch {2} cost {1}'.format(i,ob, j)) obj.append(ob) return obj ``` 也可以向自編碼器對象添加噪聲。在這種情況下，您將使用類`self._X_noisy = self.corrupt(self._X) * 0.3 + self._X * (1 - 0.3)`中定義的損壞方法，并且`fit`方法也將更改為以下內容： ```py def fit(self, X, epochs = 1, batch_size = 100): N, D = X.shape num_batches = N // batch_size obj = [] for i in range(epochs): #X = shuffle(X) for j in range(num_batches): batch = X[j * batch_size: (j * batch_size + batch_size)] _, ob = self.session.run([self._opt,self._loss], feed_dict={self._X: batch}) if j % 100 == 0: print('training epoch {0} batch {2} cost {1}'.format(i,ob, j)) obj.append(ob) return obj ``` 4. 現在，我們使用前面定義的損壞函數來生成一個嘈雜的圖像并將其提供給會話： ```py n_hidden = 800 Xtrain = trX.astype(np.float32) Xtrain_noisy = corruption(Xtrain).astype(np.float32) Xtest = teX.astype(np.float32) #noise = Xtest * np.random.randint(0, 2, Xtest.shape).astype(np.float32) Xtest_noisy = corruption(Xtest).astype(np.float32) #Xtest * (1-0.3)+ noise *(0.3) _, m = Xtrain.shape dae = DenoisingAutoEncoder(m, n_hidden) #Initialize all variables init = tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) dae.set_session(sess) err = dae.fit(Xtrain_noisy, Xtrain, epochs=10) out = dae.reconstruct(Xtest_noisy[0:100]) W1, W2, b1, b2 = dae.getWeights() red = dae.reduced_dimension(Xtrain) ``` 5. 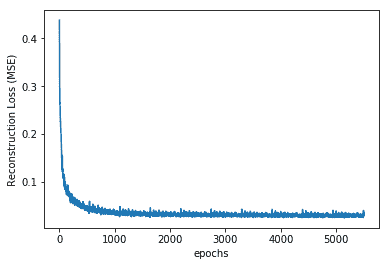隨著網絡的學習，重建損失減少： ```py plt.plot(err) plt.xlabel('epochs') plt.ylabel('Reconstruction Loss (MSE)') ``` 情節如下： ![](https://img.kancloud.cn/93/37/933775dc216e6a35588c1c92dd6bd8fd_389x266.png) 6. 當來自測試數據集的嘈雜圖像呈現給訓練網絡時，重建圖像如下： ```py # Plotting original and reconstructed images row, col = 2, 8 idx = np.random.randint(0, 100, row * col // 2) f, axarr = plt.subplots(row, col, sharex=True, sharey=True, figsize=(20,4)) for fig, row in zip([Xtest_noisy,out], axarr): for i,ax in zip(idx,row): ax.imshow(fig[i].reshape((28, 28)), cmap='Greys_r') ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) ``` 我們得到以下結果： ![](https://img.kancloud.cn/af/e6/afe6546b1b9c463a2b786808f9e3b426_1137x238.png) # 另見 * <https://cs.stanford.edu/people/karpathy/convnetjs/demo/autoencoder.html> * <http://blackecho.github.io/blog/machine-learning/2016/02/29/denoising-autoencoder-tensorflow.html> # 卷積自編碼器研究人員發現**卷積神經網絡**（**CNN**）與圖像效果最佳，因為它們可以提取隱藏在圖像中的空間信息。因此，很自然地假設，如果編碼器和解碼器網絡由 CNN 組成，它將比其余的自編碼器更好地工作，因此我們有了**卷積自編碼器**（**CAE**）。在第 4 章“卷積神經網絡”中，說明了卷積和最大池化的過程，我們將以此為基礎來了解卷積自編碼器的工作原理。 CAE 是其中編碼器和解碼器均為 CNN 網絡的一種 CAE。編碼器的卷積網絡學習將輸入編碼為一組信號，然后解碼器 CNN 嘗試從中重建輸入。它們充當通用特征提取器，并學習從輸入捕獲特征所需的最佳過濾器。 # 準備從第 4 章“卷積神經網絡”中，您了解到，隨著添加卷積層，傳遞到下一層的信息在空間范圍上會減少，但是在自編碼器中，重建的圖像應該有輸入圖像的相同的大小和深度。這意味著解碼器應以某種方式對圖像進行大小調整和卷積以重建原始圖像。與卷積一起增加空間范圍的一種方法是借助**轉置的卷積層**。通過`tf.nn.conv2d_transpose`可以輕松地在 TensorFlow 中實現這些功能，但是發現轉置的卷積層會在最終圖像中產生偽像。奧古斯都·奧德納（Augustus Odena）等。 [1]在他們的工作中表明，可以通過使用最近鄰或雙線性插值（上采樣）再加上卷積層來調整層的大小來避免這些偽像。他們通過`tf.image.resize_images`實現了最近鄰插值，取得了最佳結果；我們將在此處采用相同的方法。 # 操作步驟 1. 與往常一樣，第一步包括必要的模塊： ```py import tensorflow as tf import numpy as np from tensorflow.examples.tutorials.mnist import input_data import matplotlib.pyplot as plt import math %matplotlib inline ``` 2. 加載輸入數據： ```py mnist = input_data.read_data_sets("MNIST_data/") trX, trY, teX, teY = mnist.train.images, mnist.train.labels, mnist.test.images, mnist.test.labels ``` 3. 定義網絡參數。在這里，我們還計算每個最大池層的輸出的空間尺寸。我們需要以下信息來對解碼器網絡中的圖像進行升采樣： ```py # Network Parameters h_in, w_in = 28, 28 # Image size height and width k = 3 # Kernel size p = 2 # pool s = 2 # Strides in maxpool filters = {1:32,2:32,3:16} activation_fn=tf.nn.relu # Change in dimensions of image after each MaxPool h_l2, w_l2 = int(np.ceil(float(h_in)/float(s))) , int(np.ceil(float(w_in)/float(s))) # Height and width: second encoder/decoder layer h_l3, w_l3 = int(np.ceil(float(h_l2)/float(s))) , int(np.ceil(float(w_l2)/float(s))) # Height and width: third encoder/decoder layer ``` 4. 為輸入（嘈雜的圖像）和目標（對應的清晰圖像）創建占位符： ```py X_noisy = tf.placeholder(tf.float32, (None, h_in, w_in, 1), name='inputs') X = tf.placeholder(tf.float32, (None, h_in, w_in, 1), name='targets') ``` 5. 建立編碼器和解碼器網絡： ```py ### Encoder conv1 = tf.layers.conv2d(X_noisy, filters[1], (k,k), padding='same', activation=activation_fn) # Output size h_in x w_in x filters[1] maxpool1 = tf.layers.max_pooling2d(conv1, (p,p), (s,s), padding='same') # Output size h_l2 x w_l2 x filters[1] conv2 = tf.layers.conv2d(maxpool1, filters[2], (k,k), padding='same', activation=activation_fn) # Output size h_l2 x w_l2 x filters[2] maxpool2 = tf.layers.max_pooling2d(conv2,(p,p), (s,s), padding='same') # Output size h_l3 x w_l3 x filters[2] conv3 = tf.layers.conv2d(maxpool2,filters[3], (k,k), padding='same', activation=activation_fn) # Output size h_l3 x w_l3 x filters[3] encoded = tf.layers.max_pooling2d(conv3, (p,p), (s,s), padding='same') # Output size h_l3/s x w_l3/s x filters[3] Now 4x4x16 ### Decoder upsample1 = tf.image.resize_nearest_neighbor(encoded, (h_l3,w_l3)) # Output size h_l3 x w_l3 x filters[3] conv4 = tf.layers.conv2d(upsample1, filters[3], (k,k), padding='same', activation=activation_fn) # Output size h_l3 x w_l3 x filters[3] upsample2 = tf.image.resize_nearest_neighbor(conv4, (h_l2,w_l2)) # Output size h_l2 x w_l2 x filters[3] conv5 = tf.layers.conv2d(upsample2, filters[2], (k,k), padding='same', activation=activation_fn) # Output size h_l2 x w_l2 x filters[2] upsample3 = tf.image.resize_nearest_neighbor(conv5, (h_in,w_in)) # Output size h_in x w_in x filters[2] conv6 = tf.layers.conv2d(upsample3, filters[1], (k,k), padding='same', activation=activation_fn) # Output size h_in x w_in x filters[1] logits = tf.layers.conv2d(conv6, 1, (k,k) , padding='same', activation=None) # Output size h_in x w_in x 1 decoded = tf.nn.sigmoid(logits, name='decoded') loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=X, logits=logits) cost = tf.reduce_mean(loss) opt = tf.train.AdamOptimizer(0.001).minimize(cost) ``` 6. 啟動會話： ```py sess = tf.Session() ``` 7. 將模型擬合給定輸入： ```py epochs = 10 batch_size = 100 # Set's how much noise we're adding to the MNIST images noise_factor = 0.5 sess.run(tf.global_variables_initializer()) err = [] for i in range(epochs): for ii in range(mnist.train.num_examples//batch_size): batch = mnist.train.next_batch(batch_size) # Get images from the batch imgs = batch[0].reshape((-1, h_in, w_in, 1)) # Add random noise to the input images noisy_imgs = imgs + noise_factor * np.random.randn(*imgs.shape) # Clip the images to be between 0 and 1 noisy_imgs = np.clip(noisy_imgs, 0., 1.) # Noisy images as inputs, original images as targets batch_cost, _ = sess.run([cost, opt], feed_dict={X_noisy: noisy_imgs,X: imgs}) err.append(batch_cost) if ii%100 == 0: print("Epoch: {0}/{1}... Training loss {2}".format(i, epochs, batch_cost)) ``` 8. 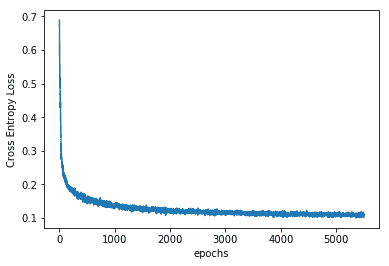網絡學習到的誤差如下： ```py plt.plot(err) plt.xlabel('epochs') plt.ylabel('Cross Entropy Loss') ``` 繪圖如下： ![](https://img.kancloud.cn/0f/20/0f20ce3fd918852dc5d41942c031fe5f_389x266.png) 9. 最后，讓我們看一下重建的圖像： ```py fig, axes = plt.subplots(rows=2, cols=10, sharex=True, sharey=True, figsize=(20,4)) in_imgs = mnist.test.images[:10] noisy_imgs = in_imgs + noise_factor * np.random.randn(*in_imgs.shape) noisy_imgs = np.clip(noisy_imgs, 0., 1.) reconstructed = sess.run(decoded, feed_dict={X_noisy: noisy_imgs.reshape((10, 28, 28, 1))}) for images, row in zip([noisy_imgs, reconstructed], axes): for img, ax in zip(images, row): ax.imshow(img.reshape((28, 28)), cmap='Greys_r') ax.get_xaxis().set_visible(False) ax.get_yaxis().set_visible(False) ``` 這是前面代碼的輸出： ![](https://img.kancloud.cn/9b/8b/9b8be20db39b71aa13a14912dd5f1f80_1452x300.png) 10. 關閉會話： ```py sess.close() ``` # 工作原理前面的 CAE 是降噪 CAE，與僅由一個瓶頸層組成的簡單降噪自編碼器相比，我們可以看到它在降噪圖像方面更好。 # 更多研究人員已將 CAE 用于語義分割。有趣的讀物是 Badrinayanan 等人在 2015 年發表的論文 [Segnet：一種用于圖像分割的深度卷積編碼器-解碼器架構](https://arxiv.org/pdf/1511.00561.pdf)。該網絡使用 VGG16 的卷積層作為其編碼器網絡，并包含一層解碼器，每個解碼器對應一個解碼器層次作為其解碼器網絡。解碼器使用從相應的編碼器接收的最大池索引，并對輸入特征圖執行非線性上采樣。本文的鏈接在本秘籍的另請參見部分以及 GitHub 鏈接中給出。 # 另見 1. <https://distill.pub/2016/deconv-checkerboard/> 2. <https://pgaleone.eu/neural-networks/2016/11/24/convolutional-autoencoders/> 3. <https://arxiv.org/pdf/1511.00561.pdf> 4. <https://github.com/arahusky/Tensorflow-Segmentation> # 棧式自編碼器到目前為止，涵蓋的自編碼器（CAE 除外）僅由單層編碼器和單層解碼器組成。但是，我們可能在編碼器和解碼器網絡中具有多層；使用更深的編碼器和解碼器網絡可以使自編碼器表示復雜的特征。這樣獲得的結構稱為棧式自編碼器（**深度自編碼器**）；由一個編碼器提取的特征將作為輸入傳遞到下一個編碼器。可以將棧式自編碼器作為一個整體網絡進行訓練，以最大程度地減少重構誤差，或者可以首先使用您先前學習的無監督方法對每個單獨的編碼器/解碼器網絡進行預訓練，然后對整個網絡進行微調。已經指出，通過預訓練，也稱為貪婪分層訓練，效果更好。 # 準備在秘籍中，我們將使用貪婪分層方法來訓練棧式自編碼器；為了簡化任務，我們將使用共享權重，因此相應的編碼器/解碼器權重將相互轉換。 # 操作步驟我們按以下步驟進行： 1. 第一步是導入所有必要的模塊： ```py import tensorflow as tf import numpy as np from tensorflow.examples.tutorials.mnist import input_data import matplotlib.pyplot as plt %matplotlib inline ``` 2. 加載數據集： ```py mnist = input_data.read_data_sets("MNIST_data/") trX, trY, teX, teY = mnist.train.images, mnist.train.labels, mnist.test.images, mnist.test.labels ``` 3. 接下來，我們定義類`StackedAutoencoder`。 `__init__`類方法包含一個列表，該列表包含從第一個輸入自編碼器和學習率開始的每個自編碼器中的許多神經元。由于每一層的輸入和輸出都有不同的尺寸，因此我們選擇字典數據結構來表示每一層的權重，偏差和輸入： ```py class StackedAutoEncoder(object): def __init__(self, list1, eta = 0.02): """ list1: [input_dimension, hidden_layer_1, ....,hidden_layer_n] """ N = len(list1)-1 self._m = list1[0] self.learning_rate = eta # Create the Computational graph self._W = {} self._b = {} self._X = {} self._X['0'] = tf.placeholder('float', [None, list1[0]]) for i in range(N): layer = '{0}'.format(i+1) print('AutoEncoder Layer {0}: {1} --> {2}'.format(layer, list1[i], list1[i+1])) self._W['E' + layer] = tf.Variable(tf.random_normal(shape=(list1[i], list1[i+1])),name='WtsEncoder'+layer) self._b['E'+ layer] = tf.Variable(np.zeros(list1[i+1]).astype(np.float32),name='BiasEncoder'+layer) self._X[layer] = tf.placeholder('float', [None, list1[i+1]]) self._W['D' + layer] = tf.transpose(self._W['E' + layer]) # Shared weights self._b['D' + layer] = tf.Variable(np.zeros(list1[i]).astype(np.float32),name='BiasDecoder' + layer) # Placeholder for inputs self._X_noisy = tf.placeholder('float', [None, self._m]) ``` 4. 我們建立一個計算圖來定義每個自編碼器的優化參數，同時進行預訓練。當先前的自編碼器的編碼器的輸出為其輸入時，它涉及為每個自編碼器定義重建損耗。為此，我們定義類方法`pretrain`和`one_pass`，它們分別為每個棧式自編碼器返回訓練操作器和編碼器的輸出： ```py self.train_ops = {} self.out = {} for i in range(N): layer = '{0}'.format(i+1) prev_layer = '{0}'.format(i) opt = self.pretrain(self._X[prev_layer], layer) self.train_ops[layer] = opt self.out[layer] = self.one_pass(self._X[prev_layer], self._W['E'+layer], self._b['E'+layer], self._b['D'+layer]) ``` 5. 我們建立計算圖以對整個棧式自編碼器進行微調。為此，我們使用類方法`encoder`和`decoder`： ```py self.y = self.encoder(self._X_noisy,N) #Encoder output self.r = self.decoder(self.y,N) # Decoder ouput optimizer = tf.train.AdamOptimizer(self.learning_rate) error = self._X['0'] - self.r # Reconstruction Error self._loss = tf.reduce_mean(tf.pow(error, 2)) self._opt = optimizer.minimize(self._loss) ``` 6. 最后，我們定義類方法`fit`，以執行每個自編碼器的分批預訓練，然后進行微調。在進行預訓練時，我們使用未損壞的輸入，而對于微調，我們使用損壞的輸入。這使我們能夠使用棧式自編碼器甚至從嘈雜的輸入中進行重構： ```py def fit(self, Xtrain, Xtr_noisy, layers, epochs = 1, batch_size = 100): N, D = Xtrain.shape num_batches = N // batch_size X_noisy = {} X = {} X_noisy ['0'] = Xtr_noisy X['0'] = Xtrain for i in range(layers): Xin = X[str(i)] print('Pretraining Layer ', i+1) for e in range(5): for j in range(num_batches): batch = Xin[j * batch_size: (j * batch_size + batch_size)] self.session.run(self.train_ops[str(i+1)], feed_dict= {self._X[str(i)]: batch}) print('Pretraining Finished') X[str(i+1)] = self.session.run(self.out[str(i+1)], feed_dict = {self._X[str(i)]: Xin}) obj = [] for i in range(epochs): for j in range(num_batches): batch = Xtrain[j * batch_size: (j * batch_size + batch_size)] batch_noisy = Xtr_noisy[j * batch_size: (j * batch_size + batch_size)] _, ob = self.session.run([self._opt,self._loss], feed_dict={self._X['0']: batch, self._X_noisy: batch_noisy}) if j % 100 == 0 : print('training epoch {0} batch {2} cost {1}'.format(i,ob, j)) obj.append(ob) return obj ``` 7. 不同的類方法如下： ```py def encoder(self, X, N): x = X for i in range(N): layer = '{0}'.format(i+1) hiddenE = tf.nn.sigmoid(tf.matmul(x, self._W['E'+layer]) + self._b['E'+layer]) x = hiddenE return x def decoder(self, X, N): x = X for i in range(N,0,-1): layer = '{0}'.format(i) hiddenD = tf.nn.sigmoid(tf.matmul(x, self._W['D'+layer]) + self._b['D'+layer]) x = hiddenD return x def set_session(self, session): self.session = session def reconstruct(self,x, n_layers): h = self.encoder(x, n_layers) r = self.decoder(h, n_layers) return self.session.run(r, feed_dict={self._X['0']: x}) def pretrain(self, X, layer ): y = tf.nn.sigmoid(tf.matmul(X, self._W['E'+layer]) + self._b['E'+layer]) r =tf.nn.sigmoid(tf.matmul(y, self._W['D'+layer]) + self._b['D'+layer]) # Objective Function error = X - r # Reconstruction Error loss = tf.reduce_mean(tf.pow(error, 2)) opt = tf.train.AdamOptimizer(.001).minimize(loss, var_list = [self._W['E'+layer],self._b['E'+layer],self._b['D'+layer]]) return opt def one_pass(self, X, W, b, c): h = tf.nn.sigmoid(tf.matmul(X, W) + b) return h ``` 8. 我們使用降噪自編碼器秘籍中定義的破壞函數來破壞圖像，最后創建一個`StackAutoencoder`并對其進行訓練： ```py Xtrain = trX.astype(np.float32) Xtrain_noisy = corruption(Xtrain).astype(np.float32) Xtest = teX.astype(np.float32) Xtest_noisy = corruption(Xtest).astype(np.float32) _, m = Xtrain.shape list1 = [m, 500, 50] # List with number of neurons in Each hidden layer, starting from input layer n_layers = len(list1)-1 autoEncoder = StackedAutoEncoder(list1) #Initialize all variables init = tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) autoEncoder.set_session(sess) err = autoEncoder.fit(Xtrain, Xtrain_noisy, n_layers, epochs=30) out = autoEncoder.reconstruct(Xtest_noisy[0:100],n_layers) ``` 9. 這里給出了隨著堆疊自編碼器的微調，重建誤差與歷時的關系。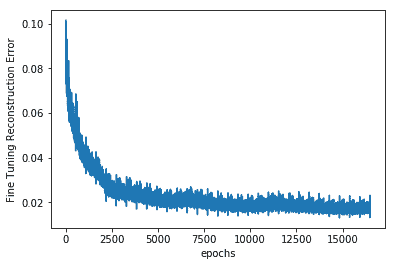您可以看到，由于進行了預訓練，我們已經從非常低的重建損失開始了： ```py plt.plot(err) plt.xlabel('epochs') plt.ylabel('Fine Tuning Reconstruction Error') ``` 情節如下： ![](https://img.kancloud.cn/42/c9/42c9d3d103cdb40d91a1a21079b65884_396x266.png) 10. 現在讓我們檢查網絡的表現。當網絡中出現嘈雜的測試圖像時，這是去噪后的手寫圖像： ![](https://img.kancloud.cn/6c/bc/6cbca24e2e266fba0c28c1dba99eba05_1137x238.png) # 工作原理在棧式自編碼器上進行的實驗表明，應以較低的學習率值進行預訓練。這樣可以確保在微調期間具有更好的收斂性和表現。 # 更多整章都是關于自編碼器的，盡管目前它們僅用于降維和信息檢索，但它們引起了很多興趣。首先，因為它們不受監督，其次，因為它們可以與 FCN 一起使用。它們可以幫助我們應對維度的詛咒。研究人員已經證明，它們也可以用于分類和異常檢測。 # 另見 * [關于棧式自編碼器的一個不錯的教程](http://ufldl.stanford.edu/wiki/index.php/Stacked_Autoencoders)。 * `Schwenk, Holger. "The diabolo classifier." Neural Computation 10.8 (1998): 2175-2200.` * `Sakurada, Mayu, and Takehisa Yairi. "Anomaly detection using autoencoders with nonlinear dimensionality reduction." Proceedings of the MLSDA 2014 2nd Workshop on Machine Learning for Sensory Data Analysis. ACM, 2014.` * [棧式自編碼器的酷 TensorBoard 可視化和實現](https://github.com/cmgreen210/TensorFlowDeepAutoencoder)