# 四、支持向量機 本章將介紹有關如何在 TensorFlow 中使用，實現和評估支持向量機（SVM）的一些重要秘籍。將涵蓋以下領域： * 使用線性 SVM * 回退到線性回歸 * 在 TensorFlow 中使用核 * 實現非線性 SVM * 實現多類 SVM > 本章中先前涵蓋的邏輯回歸和大多數 SVM 都是二元預測變量。雖然邏輯回歸試圖找到最大化距離的任何分離線（概率地），但 SVM 還嘗試最小化誤差，同時最大化類之間的余量。通常，如果問題與訓練示例相比具有大量特征，請嘗試邏輯回歸或線性 SVM。如果訓練樣本的數量較大，或者數據不是線性可分的，則可以使用具有高斯核的 SVM。 另外，請記住本章的所有代碼都可以在 [Github](https://github.com/nfmcclure/tensorflow_cookbook) 和 [Packt 倉庫](https://github.com/PacktPublishing/TensorFlow-Machine-Learning-Cookbook-Second-Edition)中找到。 # 介紹 SVM 是二分類的方法。基本思想是在兩個類之間找到二維的線性分離線（或更多維度的超平面）。我們首先假設二元類目標是 -1 或 1，而不是先前的 0 或 1 目標。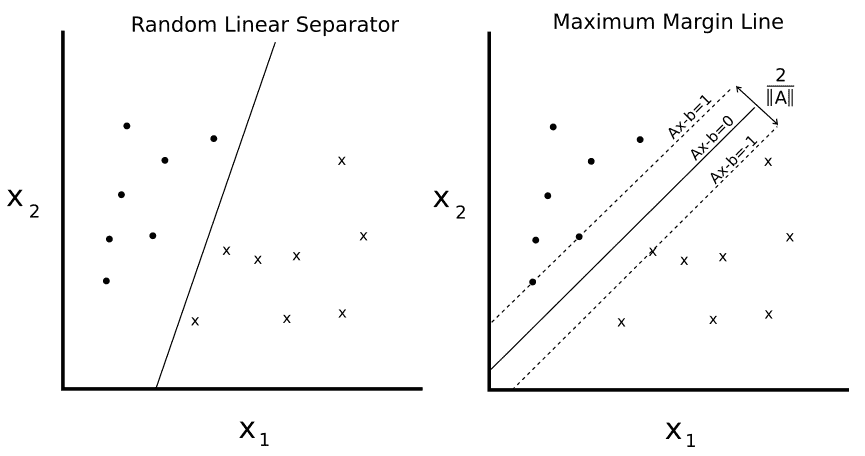由于可能有許多行分隔兩個類，我們定義最佳線性分隔符，以最大化兩個類之間的距離：  圖 1 給定兩個可分類`o`和`x`，我們希望找到兩者之間的線性分離器的等式。左側繪圖顯示有許多行將兩個類分開。右側繪圖顯示了唯一的最大邊際線。邊距寬度由`2 / ||A||`給出。通過最小化`A`的 L2 范數找到該線。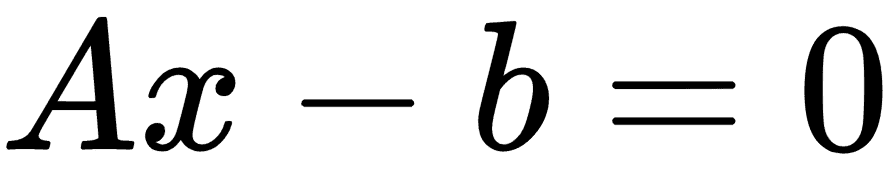 我們可以編寫如下超平面：  這里，`A`是我們部分斜率的向量，`x`是輸入向量。最大邊距的寬度可以顯示為 2 除以`A`的 L2 范數。這個事實有許多證明，但是對于幾何思想，求解從 2D 點到直線的垂直距離可以提供前進的動力。 對于線性可分的二元類數據，為了最大化余量，我們最小化`A`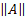，的 L2 范數。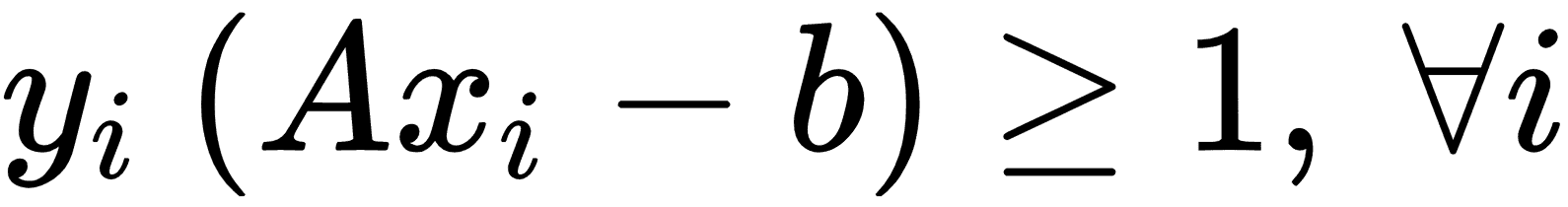我們還必須將此最小值置于以下約束條件下：  前面的約束確保我們來自相應類的所有點都在分離線的同一側。 由于并非所有數據集都是線性可分的，因此我們可以為跨越邊界線的點引入損失函數。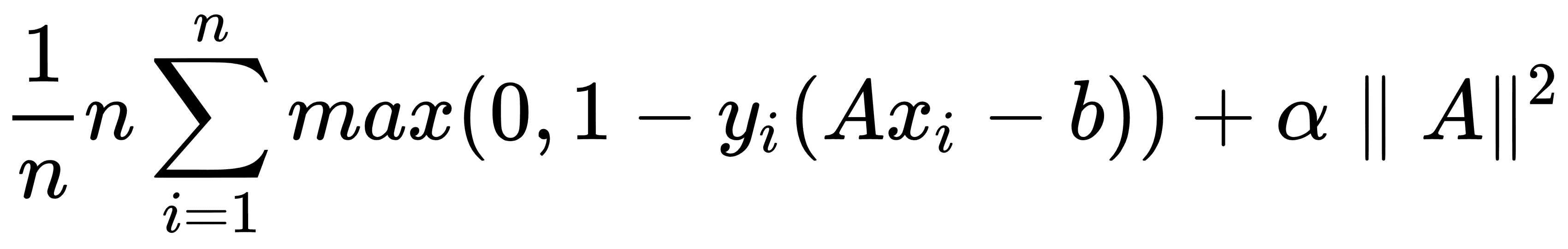對于`n`數據點，我們引入了所謂的軟邊際損失函數，如下所示：  請注意，如果該點位于邊距的正確一側，則乘積`y[i](Ax[i] - b)`始終大于 1。這使得損失函數的左手項等于 0，并且對損失函數的唯一影響是余量的大小。 前面的損失函數將尋找線性可分的線，但允許穿過邊緣線的點。根據`α`的值，這可以是硬度或軟度量。`α`的較大值導致更加強調邊距的擴大，而`α`的較小值導致模型更像是一個硬邊緣，同時允許數據點跨越邊距，如果需要的話。 在本章中，我們將建立一個軟邊界 SVM，并展示如何將其擴展到非線性情況和多個類。 # 使用線性 SVM 對于此示例，我們將從鳶尾花數據集創建線性分隔符。我們從前面的章節中知道，萼片長度和花瓣寬度創建了一個線性可分的二分類數據集，用于預測花是否是山鳶尾（I）。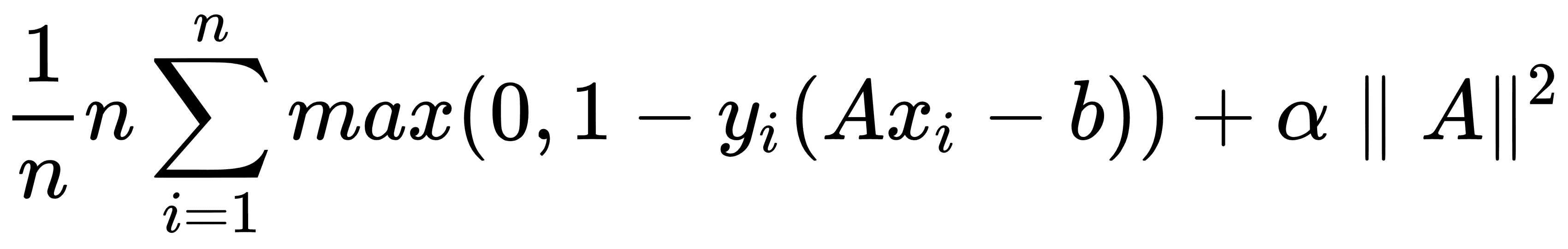 ## 準備 要在 TensorFlow 中實現軟可分 SVM，我們將實現特定的損失函數，如下所示：  這里，`A`是部分斜率的向量，`b`是截距，`x[i]`是輸入向量，`y[i]`是實際類，（-1 或 1），`α`是軟可分性正則化參數。 ## 操作步驟 我們按如下方式處理秘籍： 1. 我們首先加載必要的庫。這將包括用于訪問鳶尾數據集的`scikit-learn`數據集庫。使用以下代碼： ```py import matplotlib.pyplot as plt import numpy as np import tensorflow as tf from sklearn import datasets ``` > 要為此練習設置 scikit-learn，我們只需要輸入`$pip install -U scikit-learn`。請注意，它也安裝了 Anaconda。 1. 接下來，我們啟動圖會話并根據需要加載數據。請記住，我們正在加載鳶尾數據集中的第一個和第四個變量，因為它們是萼片長度和萼片寬度。我們正在加載目標變量，對于山鳶尾將取值 1，否則為 -1。使用以下代碼： ```py sess = tf.Session() iris = datasets.load_iris() x_vals = np.array([[x[0], x[3]] for x in iris.data]) y_vals = np.array([1 if y==0 else -1 for y in iris.target]) ``` 1. 我們現在應該將數據集拆分為訓練集和測試集。我們將評估訓練和測試集的準確率。由于我們知道這個數據集是線性可分的，因此我們應該期望在兩個集合上獲得 100% 的準確率。要拆分數據，請使用以下代碼： ```py train_indices = np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False) test_indices = np.array(list(set(range(len(x_vals))) - set(train_indices))) x_vals_train = x_vals[train_indices] x_vals_test = x_vals[test_indices] y_vals_train = y_vals[train_indices] y_vals_test = y_vals[test_indices] ``` 1. 接下來，我們設置批量大小，占位符和模型變量。值得一提的是，使用這種 SVM 算法，我們需要非常大的批量大小來幫助收斂。我們可以想象，對于非常小的批量大小，最大邊際線會略微跳躍。理想情況下，我們也會慢慢降低學習率，但現在這已經足夠了。此外，`A`變量將采用`2x1`形狀，因為我們有兩個預測變量：萼片長度和花瓣寬度。要進行此設置，我們使用以下代碼： ```py batch_size = 100 x_data = tf.placeholder(shape=[None, 2], dtype=tf.float32) y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32) A = tf.Variable(tf.random_normal(shape=[2,1])) b = tf.Variable(tf.random_normal(shape=[1,1])) ``` 1. 我們現在聲明我們的模型輸出。對于正確分類的點，如果目標是山鳶尾，則返回大于或等于 1 的數字，否則返回小于或等于 -1。模型輸出使用以下代碼： ```py model_output = tf.subtract(tf.matmul(x_data, A), b) ``` 1. 接下來，我們將匯總并聲明必要的組件以獲得最大的保證金損失。首先，我們將聲明一個計算向量的 L2 范數的函數。然后，我們添加邊距參數 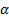。然后我們宣布我們的分類損失并將這兩項加在一起。使用以下代碼： ```py l2_norm = tf.reduce_sum(tf.square(A)) alpha = tf.constant([0.1]) classification_term = tf.reduce_mean(tf.maximum(0., tf.subtract(1., tf.multiply(model_output, y_target)))) loss = tf.add(classification _term, tf.multiply(alpha, l2_norm)) ``` 1. 現在，我們聲明我們的預測和準確率函數，以便我們可以評估訓練集和測試集的準確率，如下所示： ```py prediction = tf.sign(model_output) accuracy = tf.reduce_mean(tf.cast(tf.equal(prediction, y_target), tf.float32)) ``` 1. 在這里，我們將聲明我們的優化函數并初始化我們的模型變量；我們在以下代碼中執行此操作： ```py my_opt = tf.train.GradientDescentOptimizer(0.01) train_step = my_opt.minimize(loss) init = tf.global_variables_initializer() sess.run(init) ``` 1. 我們現在可以開始我們的訓練循環，記住我們想要在訓練和測試集上記錄我們的損失和訓練準確率，如下所示： ```py loss_vec = [] train_accuracy = [] test_accuracy = [] for i in range(500): rand_index = np.random.choice(len(x_vals_train), size=batch_size) rand_x = x_vals_train[rand_index] rand_y = np.transpose([y_vals_train[rand_index]]) sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y}) temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y}) loss_vec.append(temp_loss) train_acc_temp = sess.run(accuracy, feed_dict={x_data: x_vals_train, y_target: np.transpose([y_vals_train])}) train_accuracy.append(train_acc_temp) test_acc_temp = sess.run(accuracy, feed_dict={x_data: x_vals_test, y_target: np.transpose([y_vals_test])}) test_accuracy.append(test_acc_temp) if (i+1)%100==0: print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b))) print('Loss = ' + str(temp_loss)) ``` 1. 訓練期間腳本的輸出應如下所示： ```py Step #100 A = [[-0.10763293] [-0.65735245]] b = [[-0.68752676]] Loss = [ 0.48756418] Step #200 A = [[-0.0650763 ] [-0.89443302]] b = [[-0.73912662]] Loss = [ 0.38910741] Step #300 A = [[-0.02090022] [-1.12334013]] b = [[-0.79332656]] Loss = [ 0.28621092] Step #400 A = [[ 0.03189624] [-1.34912157]] b = [[-0.8507266]] Loss = [ 0.22397576] Step #500 A = [[ 0.05958777] [-1.55989814]] b = [[-0.9000265]] Loss = [ 0.20492229] ``` 1. 為了繪制輸出（擬合，損失和精度），我們必須提取系數并將`x`值分成山鳶尾和其它鳶尾，如下所示： ```py [[a1], [a2]] = sess.run(A) [[b]] = sess.run(b) slope = -a2/a1 y_intercept = b/a1 x1_vals = [d[1] for d in x_vals] best_fit = [] for i in x1_vals: best_fit.append(slope*i+y_intercept) setosa_x = [d[1] for i,d in enumerate(x_vals) if y_vals[i]==1] setosa_y = [d[0] for i,d in enumerate(x_vals) if y_vals[i]==1] not_setosa_x = [d[1] for i,d in enumerate(x_vals) if y_vals[i]==-1] not_setosa_y = [d[0] for i,d in enumerate(x_vals) if y_vals[i]==-1] ``` 1. 以下是使用線性分離器擬合，精度和損耗繪制數據的代碼： ```py plt.plot(setosa_x, setosa_y, 'o', label='I. setosa') plt.plot(not_setosa_x, not_setosa_y, 'x', label='Non-setosa') plt.plot(x1_vals, best_fit, 'r-', label='Linear Separator', linewidth=3) plt.ylim([0, 10]) plt.legend(loc='lower right') plt.title('Sepal Length vs Petal Width') plt.xlabel('Petal Width') plt.ylabel('Sepal Length') plt.show() plt.plot(train_accuracy, 'k-', label='Training Accuracy') plt.plot(test_accuracy, 'r--', label='Test Accuracy') plt.title('Train and Test Set Accuracies') plt.xlabel('Generation') plt.ylabel('Accuracy') plt.legend(loc='lower right') plt.show() plt.plot(loss_vec, 'k-') plt.title('Loss per Generation') plt.xlabel('Generation') plt.ylabel('Loss') plt.show() ``` > 以這種方式使用 TensorFlow 來實現 SVD 算法可能導致每次運行的結果略有不同。其原因包括隨機訓練/測試集拆分以及每個訓練批次中不同批次點的選擇。此外，在每一代之后慢慢降低學習率是理想的。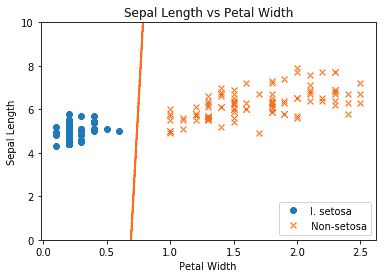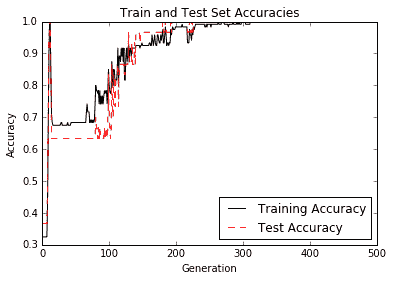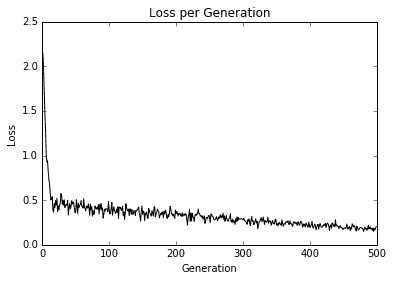 得到的圖如下：  圖 2：最終線性 SVM 與繪制的兩個類別擬合  圖 3：迭代測試和訓練集精度；我們確實獲得 100% 的準確率，因為這兩個類是線性可分的  圖 4：超過 500 次迭代的最大邊際損失圖 ## 工作原理 在本文中，我們已經證明使用最大邊際損失函數可以實現線性 SVD 模型。 # 簡化為線性回歸 SVM 可用于擬合線性回歸。在本節中，我們將探討如何使用 TensorFlow 執行此操作。 ## 準備 可以將相同的最大邊際概念應用于擬合線性回歸。我們可以考慮最大化包含最多（`x`，`y`）點的邊距，而不是最大化分隔類的邊距。為了說明這一點，我們將使用相同的鳶尾數據集，并表明我們可以使用此概念來擬合萼片長度和花瓣寬度之間的線。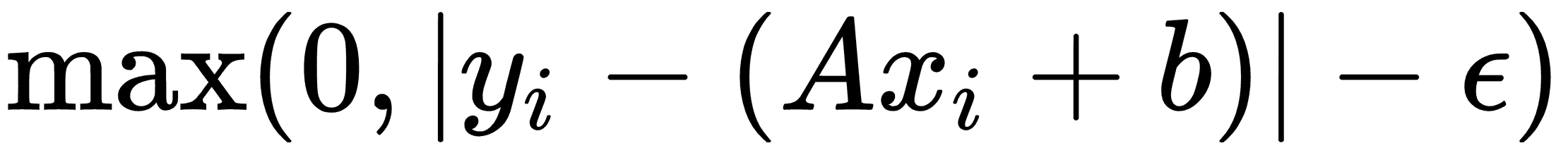 相應的損失函數類似于：  這里，`ε`是邊距寬度的一半，如果一個點位于該區域，則損失等于 0。 ## 操作步驟 我們按如下方式處理秘籍： 1. 首先，我們加載必要的庫，啟動圖，然后加載鳶尾數據集。之后，我們將數據集拆分為訓練集和測試集，以顯示兩者的損失。使用以下代碼： ```py import matplotlib.pyplot as plt import numpy as np import tensorflow as tf from sklearn import datasets sess = tf.Session() iris = datasets.load_iris() x_vals = np.array([x[3] for x in iris.data]) y_vals = np.array([y[0] for y in iris.data]) train_indices = np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False) test_indices = np.array(list(set(range(len(x_vals))) - set(train_indices))) x_vals_train = x_vals[train_indices] x_vals_test = x_vals[test_indices] y_vals_train = y_vals[train_indices] y_vals_test = y_vals[test_indices] ``` > 對于此示例，我們將數據拆分為訓練集和測試集。將數據拆分為三個數據集也很常見，其中包括驗證集。我們可以使用此驗證集來驗證我們在訓練它們時不會過擬合模型。 1. 讓我們聲明我們的批量大小，占位符和變量，并創建我們的線性模型，如下所示： ```py batch_size = 50 x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32) y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32) A = tf.Variable(tf.random_normal(shape=[1,1])) b = tf.Variable(tf.random_normal(shape=[1,1])) model_output = tf.add(tf.matmul(x_data, A), b) ``` 1. 現在，我們宣布我們的損失函數。如前文所述，損失函數實現為`ε = 0.5`。請記住，epsilon 是我們的損失函數的一部分，它允許軟邊距而不是硬邊距： ```py epsilon = tf.constant([0.5]) loss = tf.reduce_mean(tf.maximum(0., tf.subtract(tf.abs(tf.subtract(model_output, y_target)), epsilon))) ``` 1. 我們創建一個優化器并接下來初始化我們的變量，如下所示： ```py my_opt = tf.train.GradientDescentOptimizer(0.075) train_step = my_opt.minimize(loss) init = tf.global_variables_initializer() sess.run(init) ``` 1. 現在，我們迭代 200 次訓練迭代并保存訓練和測試損失以便以后繪圖： ```py train_loss = [] test_loss = [] for i in range(200): rand_index = np.random.choice(len(x_vals_train), size=batch_size) rand_x = np.transpose([x_vals_train[rand_index]]) rand_y = np.transpose([y_vals_train[rand_index]]) sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y}) temp_train_loss = sess.run(loss, feed_dict={x_data: np.transpose([x_vals_train]), y_target: np.transpose([y_vals_train])}) train_loss.append(temp_train_loss) temp_test_loss = sess.run(loss, feed_dict={x_data: np.transpose([x_vals_test]), y_target: np.transpose([y_vals_test])}) test_loss.append(temp_test_loss) if (i+1)%50==0: print('-----------') print('Generation: ' + str(i)) print('A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b))) print('Train Loss = ' + str(temp_train_loss)) print('Test Loss = ' + str(temp_test_loss)) ``` 1. 這產生以下輸出： ```py Generation: 50 A = [[ 2.20651722]] b = [[ 2.71290684]] Train Loss = 0.609453 Test Loss = 0.460152 ----------- Generation: 100 A = [[ 1.6440177]] b = [[ 3.75240564]] Train Loss = 0.242519 Test Loss = 0.208901 ----------- Generation: 150 A = [[ 1.27711761]] b = [[ 4.3149066]] Train Loss = 0.108192 Test Loss = 0.119284 ----------- Generation: 200 A = [[ 1.05271816]] b = [[ 4.53690529]] Train Loss = 0.0799957 Test Loss = 0.107551 ``` 1. 我們現在可以提取我們找到的系數，并獲得最佳擬合線的值。出于繪圖目的，我們也將獲得邊距的值。使用以下代碼： ```py [[slope]] = sess.run(A) [[y_intercept]] = sess.run(b) [width] = sess.run(epsilon) best_fit = [] best_fit_upper = [] best_fit_lower = [] for i in x_vals: best_fit.append(slope*i+y_intercept) best_fit_upper.append(slope*i+y_intercept+width) best_fit_lower.append(slope*i+y_intercept-width) ``` 1. 最后，這里是用擬合線和訓練測試損失繪制數據的代碼： ```py plt.plot(x_vals, y_vals, 'o', label='Data Points') plt.plot(x_vals, best_fit, 'r-', label='SVM Regression Line', linewidth=3) plt.plot(x_vals, best_fit_upper, 'r--', linewidth=2) plt.plot(x_vals, best_fit_lower, 'r--', linewidth=2) plt.ylim([0, 10]) plt.legend(loc='lower right') plt.title('Sepal Length vs Petal Width') plt.xlabel('Petal Width') plt.ylabel('Sepal Length') plt.show() plt.plot(train_loss, 'k-', label='Train Set Loss') plt.plot(test_loss, 'r--', label='Test Set Loss') plt.title('L2 Loss per Generation') plt.xlabel('Generation') plt.ylabel('L2 Loss') plt.legend(loc='upper right') plt.show() ``` 上述代碼的圖如下：  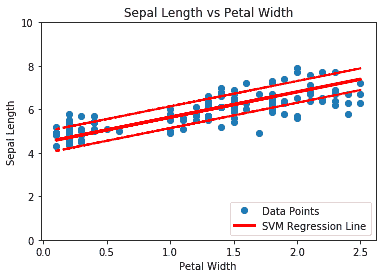圖 5：鳶尾數據上有 0.5 個邊緣的 SVM 回歸（萼片長度與花瓣寬度） 以下是訓練迭代中的訓練和測試損失：  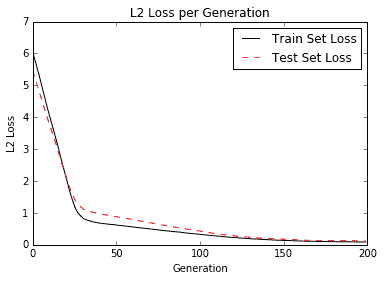圖 6：訓練和測試集上每代的 SVM 回歸損失 ## 工作原理 直覺上，我們可以將 SVM 回歸看作是一個函數，試圖盡可能多地在`2ε`寬度范圍內擬合點。該線的擬合對該參數有些敏感。如果我們選擇太小的`ε`，算法將無法適應邊距中的許多點。如果我們選擇太大的`ε`，將會有許多行能夠適應邊距中的所有數據點。我們更喜歡較小的`ε`，因為距離邊緣較近的點比較遠的點貢獻較少的損失。 # 在 TensorFlow 中使用核 先前的 SVM 使用線性可分數據。如果我們分離非線性數據，我們可以改變將線性分隔符投影到數據上的方式。這是通過更改 SVM 損失函數中的核來完成的。在本章中，我們將介紹如何更改核并分離非線性可分離數據。 ## 準備 在本文中，我們將激勵支持向量機中核的使用。在線性 SVM 部分，我們用特定的損失函數求解了軟邊界。這種方法的另一種方法是解決所謂的優化問題的對偶。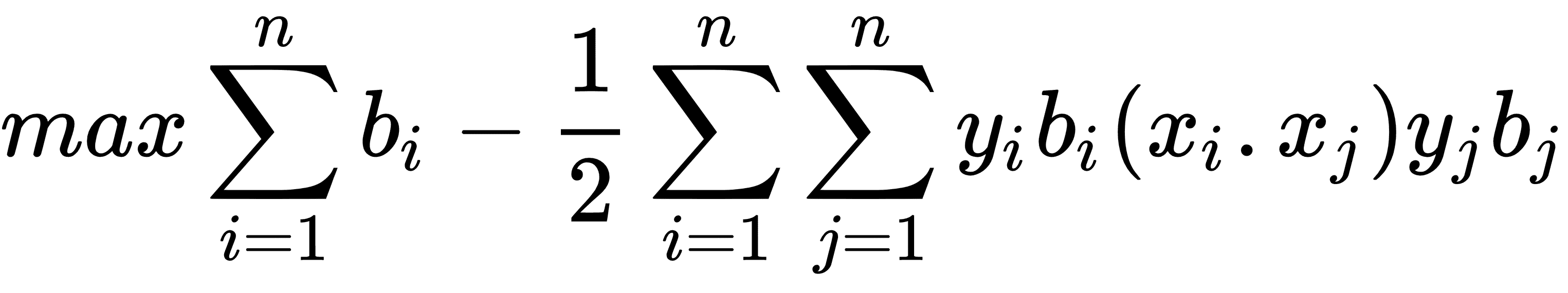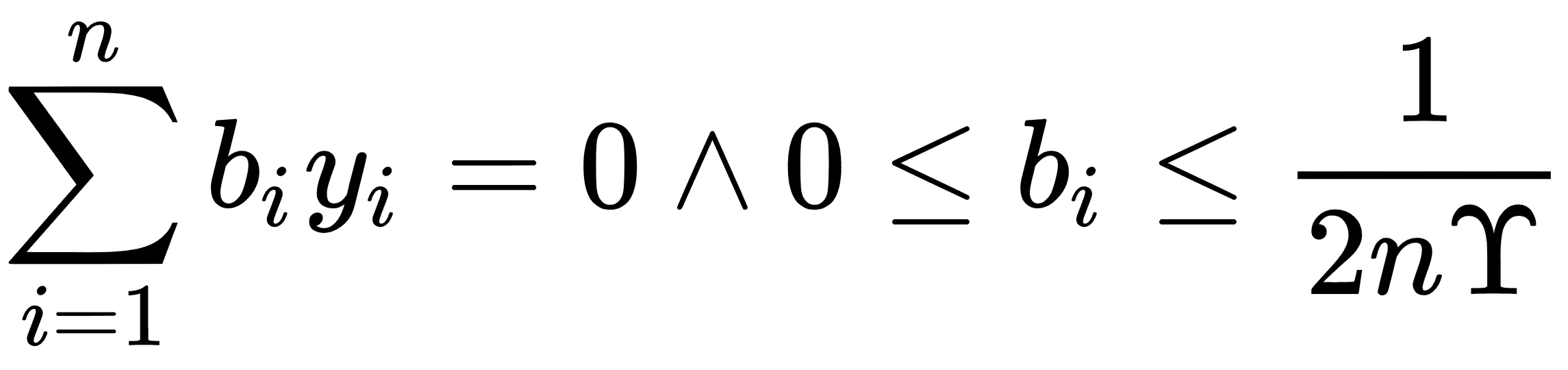可以證明線性 SVM 問題的對偶性由以下公式給出：  對此，以下適用：  這里，模型中的變量將是`b`向量。理想情況下，此向量將非常稀疏，僅對我們數據集的相應支持向量采用接近 1 和 -1 的值。我們的數據點向量由`x[i]`表示，我們的目標（1 或 -1）`y[i]`表示。 前面等式中的核是點積`x[i] · y[j]`，它給出了線性核。該核是一個方形矩陣，填充了數據點`i, j`的點積。 我們可以將更復雜的函數擴展到更高的維度，而不是僅僅在數據點之間進行點積，而在這些維度中，類可以是線性可分的。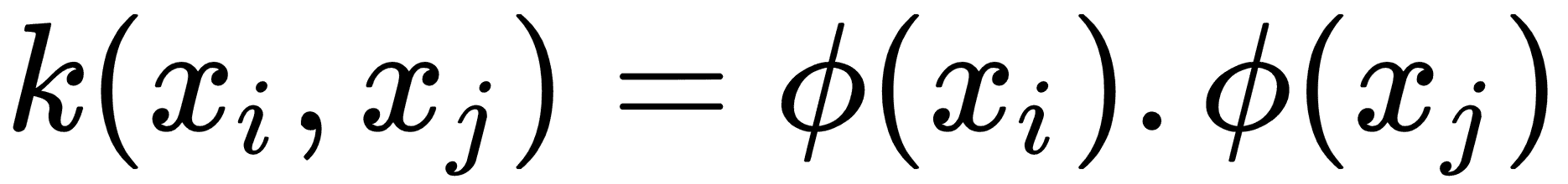這似乎是不必要的復雜，但我們可以選擇一個具有以下屬性的函數`k`：  這里`, k`被稱為核函數。更常見的核是使用高斯核（也稱為徑向基函數核或 RBF 核）。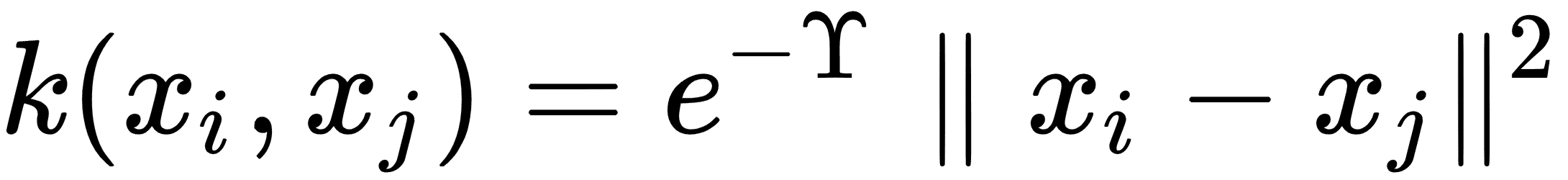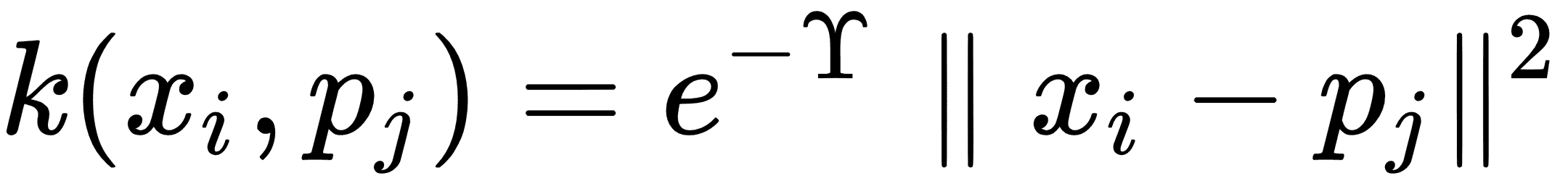該核用以下等式描述：  為了對這個核進行預測，比如說`p[i]`，我們只需在核中的相應方程中用預測點替換，如下所示：  在本節中，我們將討論如何實現高斯核。我們還將在適當的位置記下在何處替換實現線性核。我們將使用的數據集將手動創建，以顯示高斯核更適合在線性核上使用的位置。 ## 操作步驟 我們按如下方式處理秘籍： 1. 首先，我們加載必要的庫并啟動圖會話，如下所示： ```py import matplotlib.pyplot as plt import numpy as np import tensorflow as tf from sklearn import datasets sess = tf.Session() ``` 1. 現在，我們生成數據。我們將生成的數據將是兩個同心數據環；每個戒指都屬于不同的階級。我們必須確保類只有 -1 或 1。然后我們將數據分成每個類的`x`和`y`值以用于繪圖目的。為此，請使用以下代碼： ```py (x_vals, y_vals) = datasets.make_circles(n_samples=500, factor=.5, noise=.1) y_vals = np.array([1 if y==1 else -1 for y in y_vals]) class1_x = [x[0] for i,x in enumerate(x_vals) if y_vals[i]==1] class1_y = [x[1] for i,x in enumerate(x_vals) if y_vals[i]==1] class2_x = [x[0] for i,x in enumerate(x_vals) if y_vals[i]==-1] class2_y = [x[1] for i,x in enumerate(x_vals) if y_vals[i]==-1] ``` 1. 接下來，我們聲明批量大小和占位符，并創建我們的模型變量`b`。對于 SVM，我們傾向于需要更大的批量大小，因為我們需要一個非常穩定的模型，該模型在每次訓練生成時都不會波動很大。另請注意，我們為預測點添加了額外的占位符。為了可視化結果，我們將創建一個顏色網格，以查看哪些區域最后屬于哪個類。我們這樣做如下： ```py batch_size = 250 x_data = tf.placeholder(shape=[None, 2], dtype=tf.float32) y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32) prediction_grid = tf.placeholder(shape=[None, 2], dtype=tf.float32) b = tf.Variable(tf.random_normal(shape=[1,batch_size])) ``` 1. 我們現在將創建高斯核。該核可以表示為矩陣運算，如下所示： ```py gamma = tf.constant(-50.0) dist = tf.reduce_sum(tf.square(x_data), 1) dist = tf.reshape(dist, [-1,1]) sq_dists = tf.add(tf.subtract(dist, tf.multiply(2., tf.matmul(x_data, tf.transpose(x_data)))), tf.transpose(dist)) my_kernel = tf.exp(tf.multiply(gamma, tf.abs(sq_dists))) ``` > 注意`add`和`subtract`操作的`sq_dists`行中廣播的使用。 另外，請注意線性核可以表示為`my_kernel = tf.matmul(x_data, tf.transpose(x_data))`。 1. 現在，我們宣布了本秘籍中之前所述的雙重問題。最后，我們將使用`tf.negative()`函數最小化損失函數的負值，而不是最大化。我們使用以下代碼完成此任務： ```py model_output = tf.matmul(b, my_kernel) first_term = tf.reduce_sum(b) b_vec_cross = tf.matmul(tf.transpose(b), b) y_target_cross = tf.matmul(y_target, tf.transpose(y_target)) second_term = tf.reduce_sum(tf.multiply(my_kernel, tf.multiply(b_vec_cross, y_target_cross))) loss = tf.negative(tf.subtract(first_term, second_term)) ``` 1. 我們現在創建預測和準確率函數。首先，我們必須創建一個預測核，類似于步驟 4，但是我們擁有帶有預測數據的點的核心，而不是點的核。然后預測是模型輸出的符號。這實現如下： ```py rA = tf.reshape(tf.reduce_sum(tf.square(x_data), 1),[-1,1]) rB = tf.reshape(tf.reduce_sum(tf.square(prediction_grid), 1),[-1,1]) pred_sq_dist = tf.add(tf.subtract(rA, tf.multiply(2., tf.matmul(x_data, tf.transpose(prediction_grid)))), tf.transpose(rB)) pred_kernel = tf.exp(tf.multiply(gamma, tf.abs(pred_sq_dist))) prediction_output = tf.matmul(tf.multiply(tf.transpose(y_target),b), pred_kernel) prediction = tf.sign(prediction_output-tf.reduce_mean(prediction_output)) accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.squeeze(prediction), tf.squeeze(y_target)), tf.float32)) ``` > 為了實現線性預測核，我們可以編寫`pred_kernel = tf.matmul(x_data, tf.transpose(prediction_grid))`。 1. 現在，我們可以創建一個優化函數并初始化所有變量，如下所示： ```py my_opt = tf.train.GradientDescentOptimizer(0.001) train_step = my_opt.minimize(loss) init = tf.global_variables_initializer() sess.run(init) ``` 1. 接下來，我們開始訓練循環。我們將記錄每代的損耗向量和批次精度。當我們運行準確率時，我們必須放入所有三個占位符，但我們輸入`x`數據兩次以獲得對點的預測，如下所示： ```py loss_vec = [] batch_accuracy = [] for i in range(500): rand_index = np.random.choice(len(x_vals), size=batch_size) rand_x = x_vals[rand_index] rand_y = np.transpose([y_vals[rand_index]]) sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y}) temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y}) loss_vec.append(temp_loss) acc_temp = sess.run(accuracy, feed_dict={x_data: rand_x, y_target: rand_y, prediction_grid:rand_x}) batch_accuracy.append(acc_temp) if (i+1)%100==0: print('Step #' + str(i+1)) print('Loss = ' + str(temp_loss)) ``` 1. 這產生以下輸出： ```py Step #100 Loss = -28.0772 Step #200 Loss = -3.3628 Step #300 Loss = -58.862 Step #400 Loss = -75.1121 Step #500 Loss = -84.8905 ``` 1. 為了查看整個空間的輸出類，我們將在系統中創建一個預測點網格，并對所有這些預測點進行預測，如下所示： ```py x_min, x_max = x_vals[:, 0].min() - 1, x_vals[:, 0].max() + 1 y_min, y_max = x_vals[:, 1].min() - 1, x_vals[:, 1].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02)) grid_points = np.c_[xx.ravel(), yy.ravel()] [grid_predictions] = sess.run(prediction, feed_dict={x_data: x_vals, y_target: np.transpose([y_vals]), prediction_grid: grid_points}) grid_predictions = grid_predictions.reshape(xx.shape) ``` 1. 以下是繪制結果，批次準確率和損失的代碼： ```py plt.contourf(xx, yy, grid_predictions, cmap=plt.cm.Paired, alpha=0.8) plt.plot(class1_x, class1_y, 'ro', label='Class 1') plt.plot(class2_x, class2_y, 'kx', label='Class -1') plt.legend(loc='lower right') plt.ylim([-1.5, 1.5]) plt.xlim([-1.5, 1.5]) plt.show() plt.plot(batch_accuracy, 'k-', label='Accuracy') plt.title('Batch Accuracy') plt.xlabel('Generation') plt.ylabel('Accuracy') plt.legend(loc='lower right') plt.show() plt.plot(loss_vec, 'k-') plt.title('Loss per Generation') plt.xlabel('Generation') plt.ylabel('Loss') plt.show() ``` 為了簡潔起見，我們將僅顯示結果圖，但我們也可以單獨運行繪圖代碼并查看損失和準確率。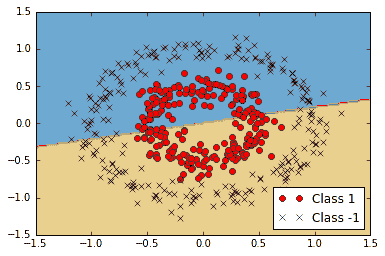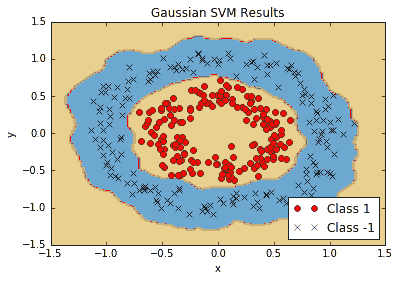 以下屏幕截圖說明了線性可分離擬合對我們的非線性數據有多糟糕：  圖 7：非線性可分離數據上的線性 SVM 以下屏幕截圖顯示了高斯核可以更好地擬合非線性數據： Figure 8: Non-linear SVM with Gaussian kernel results on non-linear ring data 如果我們使用高斯核來分離我們的非線性環數據，我們會得到更好的擬合。 ## 工作原理 有兩個重要的代碼需要了解：我們如何實現核，以及我們如何為 SVM 雙優化問題實現損失函數。我們已經展示了如何實現線性和高斯核，并且高斯核可以分離非線性數據集。 我們還應該提到另一個參數，即高斯核中的伽馬值。此參數控制影響點對分離曲率的影響程度。通常選擇小值，但它在很大程度上取決于數據集。理想情況下，使用交叉驗證等統計技術選擇此參數。 > 對于新點的預測/評估，我們使用以下命令：`sess.run(prediction, feed_dict:{x_data: x_vals, y_data: np.transpose([y_vals])})`。此評估必須包括原始數據集（`x_vals`和`y_vals`），因為 SVM 是使用支持向量定義的，由哪些點指定在邊界上或不是。 ## 更多 如果我們這樣選擇，我們可以實現更多核。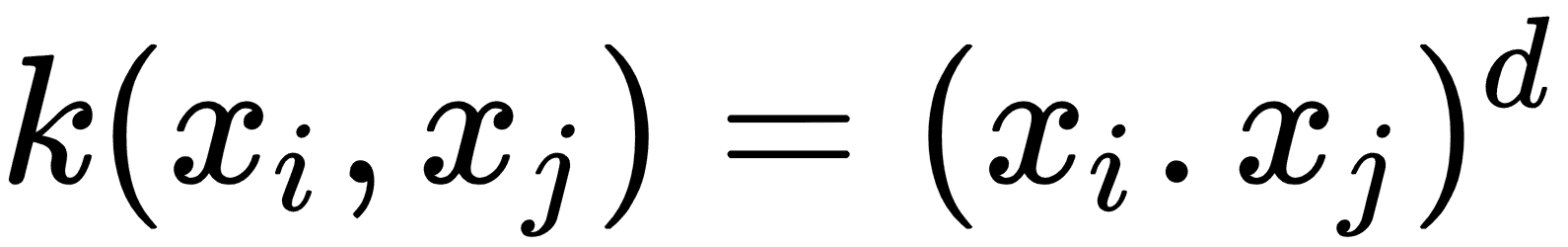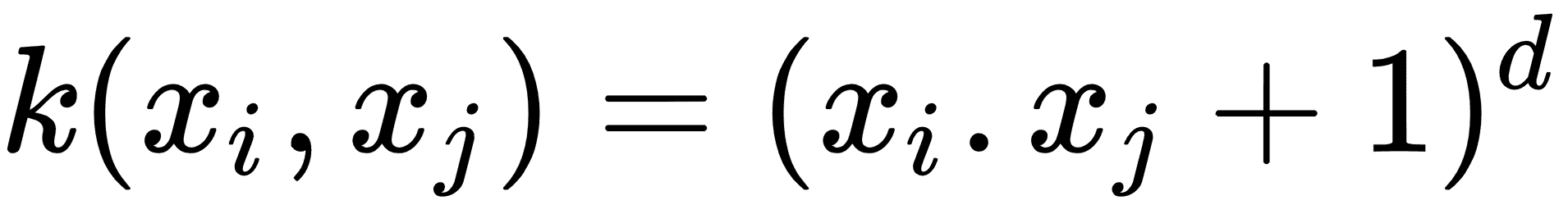以下是一些更常見的非線性核列表： * 多項式齊次核：  * 多項式非齊次核：  * 雙曲正切核：  # 實現非線性 SVM 對于此秘籍，我們將應用非線性核來拆分數據集。 ## 準備 在本節中，我們將在實際數據上實現前面的高斯核 SVM。我們將加載鳶尾數據集并為山鳶尾創建分類器（與其它鳶尾相比）。我們將看到各種伽馬值對分類的影響。 ## 操作步驟 我們按如下方式處理秘籍： 1. 我們首先加載必要的庫，其中包括`scikit-learn`數據集，以便我們可以加載鳶尾數據。然后，我們將啟動圖會話。使用以下代碼： ```py import matplotlib.pyplot as plt import numpy as np import tensorflow as tf from sklearn import datasets sess = tf.Session() ``` 1. 接下來，我們將加載鳶尾數據，提取萼片長度和花瓣寬度，并分離每個類的`x`和`y`值（以便以后繪圖），如下所示： ```py iris = datasets.load_iris() x_vals = np.array([[x[0], x[3]] for x in iris.data]) y_vals = np.array([1 if y==0 else -1 for y in iris.target]) class1_x = [x[0] for i,x in enumerate(x_vals) if y_vals[i]==1] class1_y = [x[1] for i,x in enumerate(x_vals) if y_vals[i]==1] class2_x = [x[0] for i,x in enumerate(x_vals) if y_vals[i]==-1] class2_y = [x[1] for i,x in enumerate(x_vals) if y_vals[i]==-1] ``` 1. 現在，我們聲明我們的批量大小（首選大批量），占位符和模型變量`b`，如下所示： ```py batch_size = 100 x_data = tf.placeholder(shape=[None, 2], dtype=tf.float32) y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32) prediction_grid = tf.placeholder(shape=[None, 2], dtype=tf.float32) b = tf.Variable(tf.random_normal(shape=[1,batch_size])) ``` 1. 接下來，我們聲明我們的高斯核。這個核依賴于伽馬值，我們將在本文后面的各個伽瑪值對分類的影響進行說明。使用以下代碼： ```py gamma = tf.constant(-10.0) dist = tf.reduce_sum(tf.square(x_data), 1) dist = tf.reshape(dist, [-1,1]) sq_dists = tf.add(tf.subtract(dist, tf.multiply(2., tf.matmul(x_data, tf.transpose(x_data)))), tf.transpose(dist)) my_kernel = tf.exp(tf.multiply(gamma, tf.abs(sq_dists))) # We now compute the loss for the dual optimization problem, as follows: model_output = tf.matmul(b, my_kernel) first_term = tf.reduce_sum(b) b_vec_cross = tf.matmul(tf.transpose(b), b) y_target_cross = tf.matmul(y_target, tf.transpose(y_target)) second_term = tf.reduce_sum(tf.multiply(my_kernel, tf.multiply(b_vec_cross, y_target_cross))) loss = tf.negative(tf.subtract(first_term, second_term)) ``` 1. 為了使用 SVM 執行預測，我們必須創建預測核函數。之后，我們還會聲明一個準確率計算，它只是使用以下代碼正確分類的點的百分比： ```py rA = tf.reshape(tf.reduce_sum(tf.square(x_data), 1),[-1,1]) rB = tf.reshape(tf.reduce_sum(tf.square(prediction_grid), 1),[-1,1]) pred_sq_dist = tf.add(tf.subtract(rA, tf.mul(2., tf.matmul(x_data, tf.transpose(prediction_grid)))), tf.transpose(rB)) pred_kernel = tf.exp(tf.multiply(gamma, tf.abs(pred_sq_dist))) prediction_output = tf.matmul(tf.multiply(tf.transpose(y_target),b), pred_kernel) prediction = tf.sign(prediction_output-tf.reduce_mean(prediction_output)) accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.squeeze(prediction), tf.squeeze(y_target)), tf.float32)) ``` 1. 接下來，我們聲明我們的優化函數并初始化變量，如下所示： ```py my_opt = tf.train.GradientDescentOptimizer(0.01) train_step = my_opt.minimize(loss) init = tf.initialize_all_variables() sess.run(init) ``` 1. 現在，我們可以開始訓練循環了。我們運行循環 300 次迭代并存儲損失值和批次精度。為此，我們使用以下實現： ```py loss_vec = [] batch_accuracy = [] for i in range(300): rand_index = np.random.choice(len(x_vals), size=batch_size) rand_x = x_vals[rand_index] rand_y = np.transpose([y_vals[rand_index]]) sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y}) temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y}) loss_vec.append(temp_loss) acc_temp = sess.run(accuracy, feed_dict={x_data: rand_x, y_target: rand_y, prediction_grid:rand_x}) batch_accuracy.append(acc_temp) ``` 1. 為了繪制決策邊界，我們將創建`x`，`y`點的網格并評估我們在所有這些點上創建的預測函數，如下所示： ```py x_min, x_max = x_vals[:, 0].min() - 1, x_vals[:, 0].max() + 1 y_min, y_max = x_vals[:, 1].min() - 1, x_vals[:, 1].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02)) grid_points = np.c_[xx.ravel(), yy.ravel()] [grid_predictions] = sess.run(prediction, feed_dict={x_data: x_vals, y_target: np.transpose([y_vals]), prediction_grid: grid_points}) grid_predictions = grid_predictions.reshape(xx.shape) ``` 1. 為簡潔起見，我們只展示如何用決策邊界繪制點。有關伽馬值的圖和效果，請參閱本秘籍的下一部分。使用以下代碼： ```py plt.contourf(xx, yy, grid_predictions, cmap=plt.cm.Paired, alpha=0.8) plt.plot(class1_x, class1_y, 'ro', label='I. setosa') plt.plot(class2_x, class2_y, 'kx', label='Non-setosa') plt.title('Gaussian SVM Results on Iris Data') plt.xlabel('Petal Length') plt.ylabel('Sepal Width') plt.legend(loc='lower right') plt.ylim([-0.5, 3.0]) plt.xlim([3.5, 8.5]) plt.show() ``` ## 工作原理 以下是對四種不同伽瑪值（1，10，25 和 100）的山鳶尾結果的分類。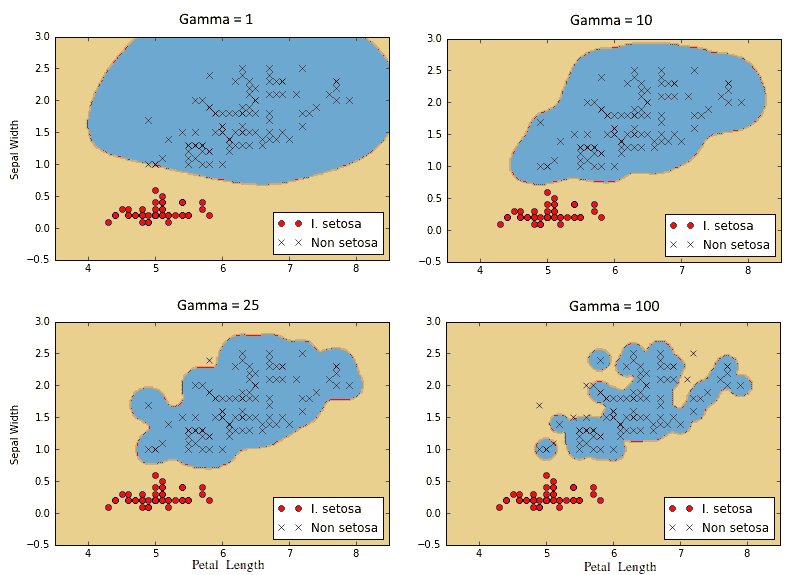注意伽瑪值越高，每個單獨點對分類邊界的影響越大：  圖 9：使用具有四個不同伽馬值的高斯核 SVM 的山鳶尾的分類結果 # 實現多類 SVM 我們還可以使用 SVM 對多個類進行分類，而不僅僅是兩個類。在本文中，我們將使用多類 SVM 對鳶尾數據集中的三種類型的花進行分類。 ## 準備 通過設計，SVM 算法是二元分類器。但是，有一些策略可以讓他們在多個類上工作。兩種主要策略稱為“一對一”，“一對剩余”。 一對一是一種策略，其中為每個可能的類對創建二分類器。然后，對具有最多投票的類的點進行預測。這可能在計算上很難，因為我們必須為`k`類創建`k!/(k - 2)!2!`個分類器。 實現多類分類器的另一種方法是執行一對一策略，我們為`k`類的每個類創建一個分類器。點的預測類將是創建最大 SVM 邊距的類。這是我們將在本節中實現的策略。 在這里，我們將加載鳶尾數據集并使用高斯核執行多類非線性 SVM。鳶尾數據集是理想的，因為有三個類（山鳶尾，弗吉尼亞和雜色鳶尾）。我們將為每個類創建三個高斯核 SVM，并預測存在最高邊界的點。 ## 操作步驟 我們按如下方式處理秘籍： 1. 首先，我們加載我們需要的庫并啟動圖，如下所示： ```py import matplotlib.pyplot as plt import numpy as np import tensorflow as tf from sklearn import datasets sess = tf.Session() ``` 1. 接下來，我們將加載鳶尾數據集并拆分每個類的目標。我們將僅使用萼片長度和花瓣寬度來說明，因為我們希望能夠繪制輸出。我們還將每個類的`x`和`y`值分開，以便最后進行繪圖。使用以下代碼： ```py iris = datasets.load_iris() x_vals = np.array([[x[0], x[3]] for x in iris.data]) y_vals1 = np.array([1 if y==0 else -1 for y in iris.target]) y_vals2 = np.array([1 if y==1 else -1 for y in iris.target]) y_vals3 = np.array([1 if y==2 else -1 for y in iris.target]) y_vals = np.array([y_vals1, y_vals2, y_vals3]) class1_x = [x[0] for i,x in enumerate(x_vals) if iris.target[i]==0] class1_y = [x[1] for i,x in enumerate(x_vals) if iris.target[i]==0] class2_x = [x[0] for i,x in enumerate(x_vals) if iris.target[i]==1] class2_y = [x[1] for i,x in enumerate(x_vals) if iris.target[i]==1] class3_x = [x[0] for i,x in enumerate(x_vals) if iris.target[i]==2] class3_y = [x[1] for i,x in enumerate(x_vals) if iris.target[i]==2] ``` 1. 與實現非線性 SVM 秘籍相比，我們在此示例中所做的最大改變是，許多維度將發生變化（我們現在有三個分類器而不是一個）。我們還將利用矩陣廣播和重塑技術一次計算所有三個 SVM。由于我們一次性完成這一操作，我們的`y_target`占位符現在具有`[3, None]`的大小，我們的模型變量`b`將被初始化為`[3, batch_size]`。使用以下代碼： ```py batch_size = 50 x_data = tf.placeholder(shape=[None, 2], dtype=tf.float32) y_target = tf.placeholder(shape=[3, None], dtype=tf.float32) prediction_grid = tf.placeholder(shape=[None, 2], dtype=tf.float32) b = tf.Variable(tf.random_normal(shape=[3,batch_size])) ``` 1. 接下來，我們計算高斯核。由于這僅取決于輸入的 x 數據，因此該代碼不會改變先前的秘籍。使用以下代碼： ```py gamma = tf.constant(-10.0) dist = tf.reduce_sum(tf.square(x_data), 1) dist = tf.reshape(dist, [-1,1]) sq_dists = tf.add(tf.subtract(dist, tf.multiply(2., tf.matmul(x_data, tf.transpose(x_data)))), tf.transpose(dist)) my_kernel = tf.exp(tf.multiply(gamma, tf.abs(sq_dists))) ``` 1. 一個重大變化是我們將進行批量矩陣乘法。我們將最終得到三維矩陣，我們將希望在第三個索引上廣播矩陣乘法。我們沒有為此設置數據和目標矩陣。為了使`x^T · x`等操作跨越額外維度，我們創建一個函數來擴展這樣的矩陣，將矩陣重新整形為轉置，然后在額外維度上調用 TensorFlow 的`batch_matmul`。使用以下代碼： ```py def reshape_matmul(mat): v1 = tf.expand_dims(mat, 1) v2 = tf.reshape(v1, [3, batch_size, 1]) return tf.batch_matmul(v2, v1) ``` 1. 創建此函數后，我們現在可以計算雙重損失函數，如下所示： ```py model_output = tf.matmul(b, my_kernel) first_term = tf.reduce_sum(b) b_vec_cross = tf.matmul(tf.transpose(b), b) y_target_cross = reshape_matmul(y_target) second_term = tf.reduce_sum(tf.multiply(my_kernel, tf.multiply(b_vec_cross, y_target_cross)),[1,2]) loss = tf.reduce_sum(tf.negative(tf.subtract(first_term, second_term))) ``` 1. 現在，我們可以創建預測核。請注意，我們必須小心`reduce_sum`函數并且不要在所有三個 SVM 預測中減少，因此我們必須告訴 TensorFlow 不要用第二個索引參數對所有內容求和。使用以下代碼： ```py rA = tf.reshape(tf.reduce_sum(tf.square(x_data), 1),[-1,1]) rB = tf.reshape(tf.reduce_sum(tf.square(prediction_grid), 1),[-1,1]) pred_sq_dist = tf.add(tf.subtract(rA, tf.multiply(2., tf.matmul(x_data, tf.transpose(prediction_grid)))), tf.transpose(rB)) pred_kernel = tf.exp(tf.multiply(gamma, tf.abs(pred_sq_dist))) ``` 1. 當我們完成預測核時，我們可以創建預測。這里的一個重大變化是預測不是輸出的`sign()`。由于我們正在實現一對一策略，因此預測是具有最大輸出的分類器。為此，我們使用 TensorFlow 的內置`argmax()`函數，如下所示： ```py prediction_output = tf.matmul(tf.mul(y_target,b), pred_kernel) prediction = tf.arg_max(prediction_output-tf.expand_dims(tf.reduce_mean(prediction_output,1), 1), 0) accuracy = tf.reduce_mean(tf.cast(tf.equal(prediction, tf.argmax(y_target,0)), tf.float32)) ``` 1. 現在我們已經擁有了核，損失和預測函數，我們只需要聲明我們的優化函數并初始化我們的變量，如下所示： ```py my_opt = tf.train.GradientDescentOptimizer(0.01) train_step = my_opt.minimize(loss) init = tf.global_variables_initializer() sess.run(init) ``` 1. 該算法收斂速度相對較快，因此我們不必運行訓練循環超過 100 次迭代。我們使用以下代碼執行此操作： ```py loss_vec = [] batch_accuracy = [] for i in range(100): rand_index = np.random.choice(len(x_vals), size=batch_size) rand_x = x_vals[rand_index] rand_y = y_vals[:,rand_index] sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y}) temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y}) loss_vec.append(temp_loss) acc_temp = sess.run(accuracy, feed_dict={x_data: rand_x, y_target: rand_y, prediction_grid:rand_x}) batch_accuracy.append(acc_temp) if (i+1)%25==0: print('Step #' + str(i+1)) print('Loss = ' + str(temp_loss)) Step #25 Loss = -2.8951 Step #50 Loss = -27.9612 Step #75 Loss = -26.896 Step #100 Loss = -30.2325 ``` 1. 我們現在可以創建點的預測網格并對所有點運行預測函數，如下所示： ```py x_min, x_max = x_vals[:, 0].min() - 1, x_vals[:, 0].max() + 1 y_min, y_max = x_vals[:, 1].min() - 1, x_vals[:, 1].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02)) grid_points = np.c_[xx.ravel(), yy.ravel()] grid_predictions = sess.run(prediction, feed_dict={x_data: rand_x, y_target: rand_y, prediction_grid: grid_points}) grid_predictions = grid_predictions.reshape(xx.shape) ``` 1. 以下是繪制結果，批量準確率和損失函數的代碼。為簡潔起見，我們只顯示最終結果： ```py plt.contourf(xx, yy, grid_predictions, cmap=plt.cm.Paired, alpha=0.8) plt.plot(class1_x, class1_y, 'ro', label='I. setosa') plt.plot(class2_x, class2_y, 'kx', label='I. versicolor') plt.plot(class3_x, class3_y, 'gv', label='I. virginica') plt.title('Gaussian SVM Results on Iris Data') plt.xlabel('Petal Length') plt.ylabel('Sepal Width') plt.legend(loc='lower right') plt.ylim([-0.5, 3.0]) plt.xlim([3.5, 8.5]) plt.show() plt.plot(batch_accuracy, 'k-', label='Accuracy') plt.title('Batch Accuracy') plt.xlabel('Generation') plt.ylabel('Accuracy') plt.legend(loc='lower right') plt.show() plt.plot(loss_vec, 'k-') plt.title('Loss per Generation') plt.xlabel('Generation') plt.ylabel('Loss') plt.show() ``` 然后我們得到以下繪圖：  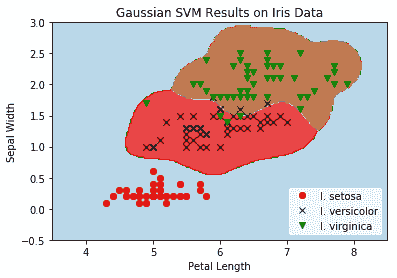圖 10：在鳶尾數據集上的伽馬為 10 的多類（三類）非線性高斯 SVM 的結果 我們觀察前面的屏幕截圖，其中顯示了所有三個鳶尾類，以及為每個類分類的點網格。 ## 工作原理 本文中需要注意的重點是我們如何改變算法以同時優化三個 SVM 模型。我們的模型參數`b`有一個額外的維度可以考慮所有三個模型。在這里，我們可以看到，由于 TensorFlow 處理額外維度的內置函數，算法擴展到多個類似算法相對容易。 下一章將介紹最近鄰方法，這是一種用于預測目的的非常強大的算法。