# 十一、更多 TensorFlow 在本章中，我們將介紹以下秘籍： * 在 TensorBoard 中可視化的圖 * 使用遺傳算法 * 使用 K 均值聚類 * 求解常微分方程組 * 使用隨機森林 * 使用 TensorFlow 和 Keras 本章中出現的所有代碼均可在 [Github](https://github.com/nfmcclure/tensorflow_cookbook) 和 [Packt 倉庫](https://github.com/PacktPublishing/TensorFlow-Machine-Learning-Cookbook-Second-Edition)中在線獲取。 # 介紹 在本書中，我們已經看到 TensorFlow 能夠實現許多模型，但 TensorFlow 可以做更多。本章將向您展示其中的一些內容。我們將首先展示如何使用 TensorBoard 的各個方面，這是 TensorFlow 附帶的一項功能，它允許我們在模型訓練時可視化摘要指標，圖和圖像。本章中的其余秘籍將展示如何使用 TensorFlow 的`group()`函數進行逐步更新。該函數將允許我們實現遺傳算法，執行 k 均值聚類，求解 ODE 系統，甚至創建梯度提升隨機森林。 # 可視化 TensorBoard 中的圖 監視和排除機器學習算法可能是一項艱巨的任務，尤其是在您知道結果之前必須等待很長時間才能完成訓練。為了解決這個問題，TensorFlow 包含一個名為 TensorBoard 的計算圖可視化工具。使用 TensorBoard，即使在訓練期間，我們也可以可視化和繪制重要值（損失，準確率，批次訓練時間等）。 ## 準備 為了說明我們可以使用 TensorBoard 的各種方法，我們將從第 3 章，線性回歸中的線性回歸方法的 TensorFlow 方法重新實現線性回歸模型。我們將生成帶有誤差的線性數據，并使用 TensorFlow 損失和反向傳播來匹配數據線。我們將展示如何監控數值，值集的直方圖以及如何在 TensorBoard 中創建圖像。 ## 操作步驟 1. 首先，我們將加載腳本所需的庫： ```py import os import io import time import numpy as np import matplotlib.pyplot as plt import tensorflow as tf ``` 1. 我們現在將初始化一個會話并創建一個可以將 TensorBoard 摘要寫入`tensorboard`文件夾的摘要編寫器： ```py sess = tf.Session() # Create a visualizer object summary_writer = tf.summary.FileWriter('tensorboard', sess.graph) ``` 1. 我們需要確保`tensorboard`文件夾存在，以便摘要編寫者編寫`tensorboard`日志： ```py if not os.path.exists('tensorboard'): os.makedirs('tensorboard') ``` 1. 我們現在將設置模型參數并生成模型的線性數據。請注意，由于我們生成數據的方式，我們的真實斜率值是`2`。我們將隨著時間的推移想象出變化的斜率，并看到它接近真正的值： ```py batch_size = 50 generations = 100 # Create sample input data x_data = np.arange(1000)/10\. true_slope = 2\. y_data = x_data * true_slope + np.random.normal(loc=0.0, scale=25, size=1000) ``` 1. 接下來，我們將數據集拆分為訓練和測試集： ```py train_ix = np.random.choice(len(x_data), size=int(len(x_data)*0.9), replace=False) test_ix = np.setdiff1d(np.arange(1000), train_ix) x_data_train, y_data_train = x_data[train_ix], y_data[train_ix] x_data_test, y_data_test = x_data[test_ix], y_data[test_ix] ``` 1. 現在我們可以創建占位符，變量，模型運算，損失和優化操作： ```py x_graph_input = tf.placeholder(tf.float32, [None]) y_graph_input = tf.placeholder(tf.float32, [None]) # Declare model variables m = tf.Variable(tf.random_normal([1], dtype=tf.float32), name='Slope') # Declare model output = tf.multiply(m, x_graph_input, name='Batch_Multiplication') # Declare loss function (L1) residuals = output - y_graph_input l2_loss = tf.reduce_mean(tf.abs(residuals), name="L2_Loss") # Declare optimization function my_optim = tf.train.GradientDescentOptimizer(0.01) train_step = my_optim.minimize(l2_loss) ``` 1. 我們現在可以創建一個 TensorBoard 操作來匯總標量值。我們將總結的標量值是模型的斜率估計值： ```py with tf.name_scope('Slope_Estimate'): tf.summary.scalar('Slope_Estimate', tf.squeeze(m)) ``` 1. 我們可以添加到 TensorBoard 的另一個摘要是直方圖摘要，它在張量中輸入多個值并輸出圖和直方圖： ```py with tf.name_scope('Loss_and_Residuals'): tf.summary.histogram('Histogram_Errors', tf.squeeze(l1_loss)) tf.summary.histogram('Histogram_Residuals', tf.squeeze(residuals)) ``` 1. 創建這些摘要操作后，我們需要創建一個將所有摘要組合在一起的摘要合并操作。然后我們可以初始化模型變量： ```py summary_op = tf.summary.merge_all() # Initialize Variables init = tf.global_variables_initializer() sess.run(init) ``` 1. 現在，我們可以訓練線性模型并編寫每一代的摘要： ```py for i in range(generations): batch_indices = np.random.choice(len(x_data_train), size=batch_size) x_batch = x_data_train[batch_indices] y_batch = y_data_train[batch_indices] _, train_loss, summary = sess.run([train_step, l2_loss, summary_op], feed_dict={x_graph_input: x_batch, y_graph_input: y_batch}) test_loss, test_resids = sess.run([l2_loss, residuals], feed_dict={x_graph_input: x_data_test, y_graph_input: y_data_test}) if (i+1)%10==0: print('Generation {} of {}. Train Loss: {:.3}, Test Loss: {:.3}.'.format(i+1, generations, train_loss, test_loss)) log_writer = tf.train.SummaryWriter('tensorboard') log_writer.add_summary(summary, i) ``` 1. 為了將最終的線性擬合圖與 TensorBoard 中的數據點放在一起，我們必須以`protobuf`格式創建圖的圖像。為此，我們將創建一個輸出`protobuf`圖像的函數： ```py def gen_linear_plot(slope): linear_prediction = x_data * slope plt.plot(x_data, y_data, 'b.', label='data') plt.plot(x_data, linear_prediction, 'r-', linewidth=3, label='predicted line') plt.legend(loc='upper left') buf = io.BytesIO() plt.savefig(buf, format='png') buf.seek(0) return(buf) ``` 1. 現在，我們可以創建`protobuf`圖像并將其添加到 TensorBoard： ```py # Get slope value slope = sess.run(m) # Generate the linear plot in buffer plot_buf = gen_linear_plot(slope[0]) # Convert PNG buffer to TF image image = tf.image.decode_png(plot_buf.getvalue(), channels=4) # Add the batch dimension image = tf.expand_dims(image, 0) # Add image summary image_summary_op = tf.summary.image("Linear_Plot", image) image_summary = sess.run(image_summary_op) log_writer.add_summary(image_summary, i) log_writer.close() ``` Be careful writing image summaries too often to TensorBoard. For example, if we were to write an image summary every generation for 10,000 generations, that would generate 10,000 images worth of summary data. This tends to eat up disk space very quickly. ## 更多 1. 由于我們要從命令行運行描述的 python 腳本，我們打開命令提示符并運行以下命令： ```py $ python3 using_tensorboard.py Run the command: $tensorboard --logdir="tensorboard" Then navigate to http://127.0.0.0:6006 Generation 10 of 100\. Train Loss: 20.4, Test Loss: 20.5\. Generation 20 of 100\. Train Loss: 17.6, Test Loss: 20.5\. Generation 90 of 100\. Train Loss: 20.1, Test Loss: 20.5\. Generation 100 of 100\. Train Loss: 19.4, Test Loss: 20.5\. ``` 1. 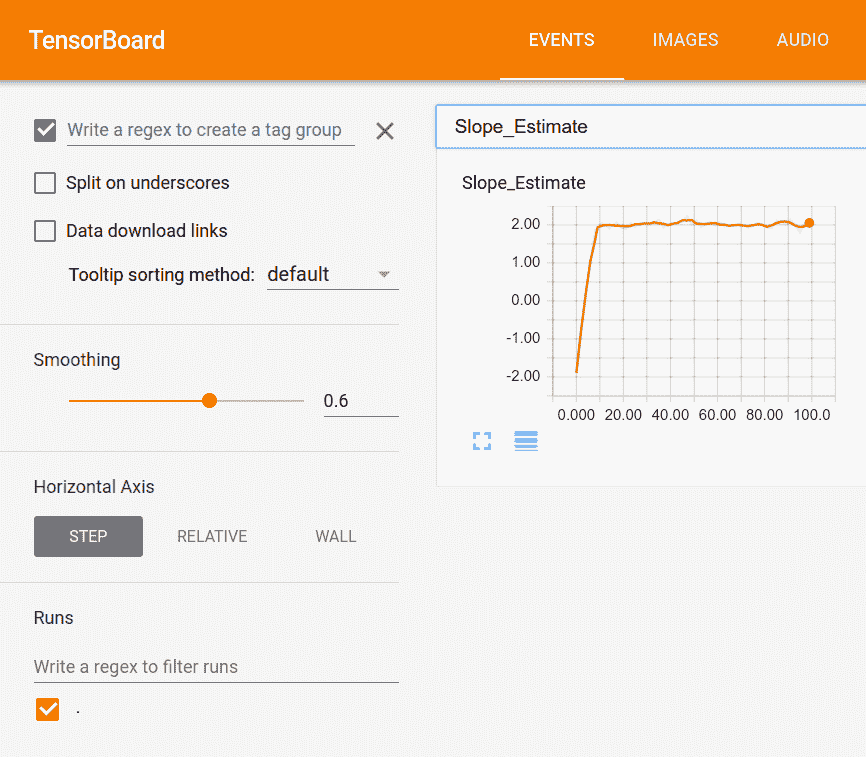然后我們將運行前面指定的命令來啟動 tensorboard： ```py $ tensorboard --logdir="tensorboard" Starting tensorboard b'29' on port 6006 (You can navigate to http://127.0.0.1:6006) ``` 以下是我們在 TensorBoard 中可以看到的示例：  圖 1：標量值，我們的斜率估計，在張量板中可視化 在這里，我們可以看到我們的標量總結的 100 代的繪圖，斜率估計。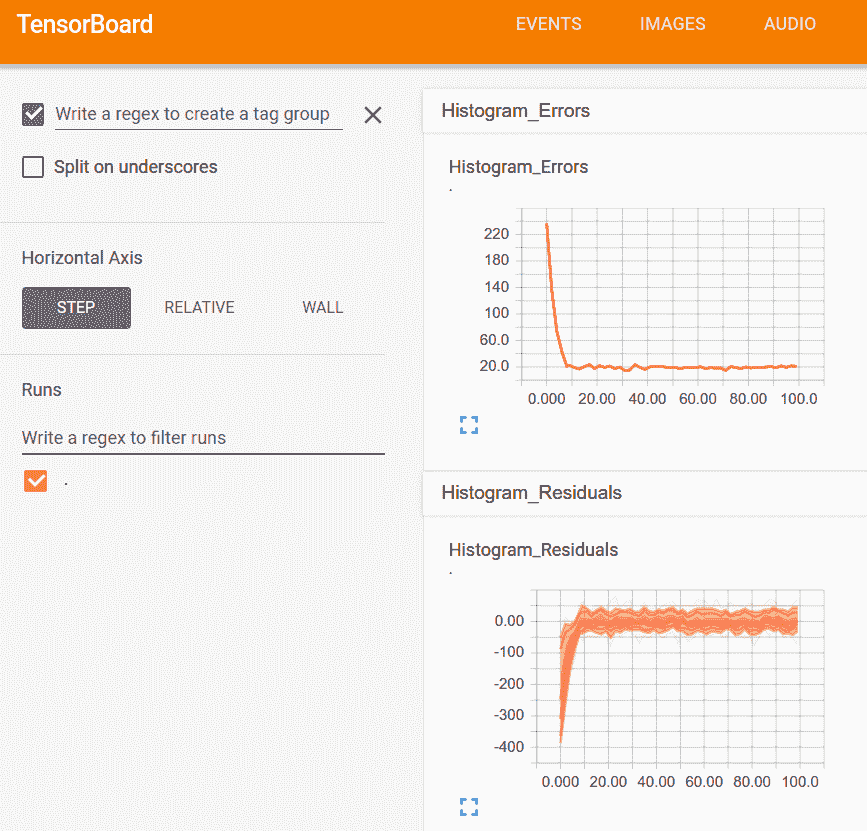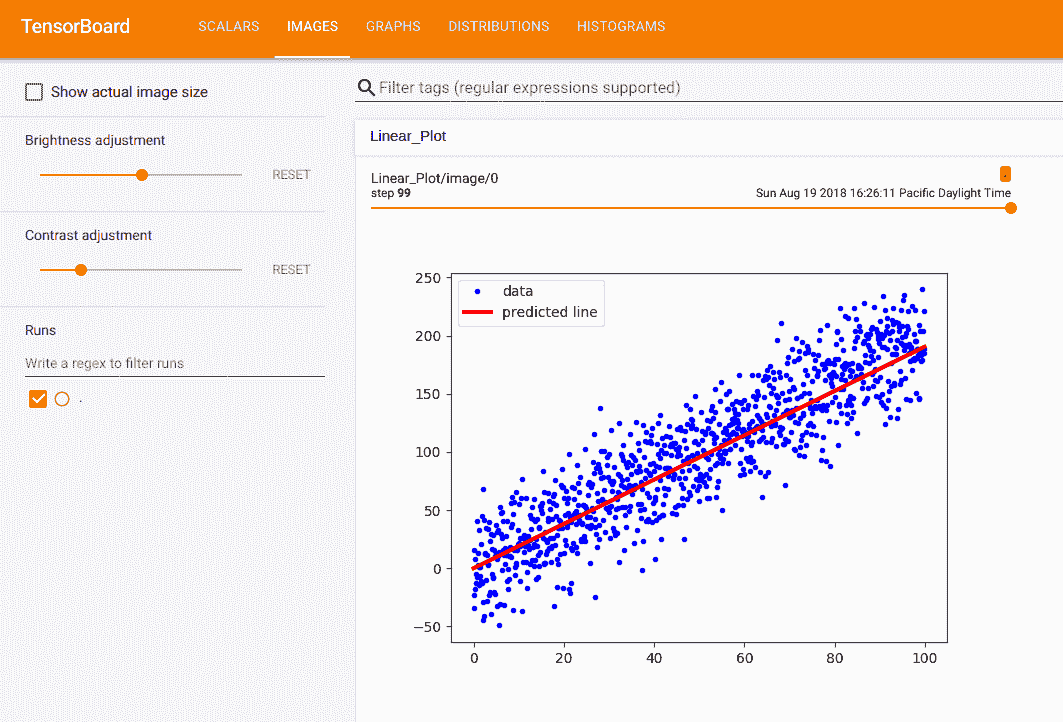事實上，我們可以看到它確實接近`2`的真正值：  圖 2：在這里，我們可視化模型的誤差和殘差的直方圖 上圖顯示了查看直方圖摘要的一種方法，可以將其視為多個折線圖：  圖 3：張量板中插入的圖片 前面是我們以`protobuf`格式放入的最終擬合和數據點圖，并插入到 TensorBoard 中的圖像摘要中。 # 使用遺傳算法 TensorFlow 還可用于更新我們可以在計算圖中表達的任何迭代算法。一種這樣的迭代算法是遺傳算法，即優化過程。 ## 準備 在本文中，我們將說明如何實現簡單的遺傳算法。遺傳算法是優化任何參數空間（離散，連續，平滑，非平滑等）的一種方法。我們的想法是創建一組隨機初始化的解決方案，并應用選擇，重組和變異來生成新的（可能更好的）子解決方案。整個想法取決于我們可以通過查看個人解決問題的程度來計算個體解決方案的適用性。 通常，遺傳算法的概要是從隨機初始化的群體開始，根據它們的適應性對它們進行排序，然后選擇最適合的個體來隨機重組（或交叉）以創建新的子解決方案。然后，這些子解決方案會稍微突變，以產生新的和看不見的改進，然后再添加回父群體。在我們將子代和父代結合起來之后，我們再次重復整個過程。 停止遺傳算法的標準各不相同，但出于我們的目的，我們將迭代它們一定數量的世代。當我們最適合的人達到理想的適應水平或者在這么多代之后最大適應度沒有改變時，我們也可以停止。 對于這個秘籍，我們將簡單地說明如何在 Tensorflow 中執行此操作。我們要解決的問題是生成一個最接近地面實況函數的個體（50 個浮點數的數組）`f(x) = sin(2πx / 50)`。適應度將是個體與地面事實之間的均方誤差（越高越好）的負值。 ## 操作步驟 1. 我們首先加載腳本所需的庫： ```py import os import numpy as np import matplotlib.pyplot as plt import tensorflow as tf ``` 1. 接下來，我們將設置遺傳算法的參數。在這里，我們將有`100`個體，每個個體的長度為`50`。選擇百分比為 20%（保持前 20 名個人）。突變將被設置為特征數量的倒數，這是突變開始的常見位置。這意味著我們希望每個子解決方案的一個特征發生變化。我們將為`200`世代運行遺傳算法： ```py pop_size = 100 features = 50 selection = 0.2 mutation = 1./ features generations = 200 num_parents = int(pop_size*selection) num_children = pop_size - num_parents ``` 1. 我們將初始化圖會話并創建基礎事實函數，我們將使用它來快速計算適應度： ```py sess = tf.Session() # Create ground truth truth = np.sin(2*np.pi*(np.arange(features, dtype=np.float32))/features) ``` 1. 接下來，我們將`population`初始化為具有隨機正常輸入的 TensorFlow 變量： ```py population = tf.Variable(np.random.randn(pop_size, features), dtype=tf.float32) ``` 1. 我們現在可以為遺傳算法創建占位符。占位符是為了事實，也是為了每一代都會改變的數據。由于我們希望父代之間的交叉位置發生變化，并且變異概率/值會發生變化，因此這些將是我們模型中的占位符： ```py truth_ph = tf.placeholder(tf.float32, [1, features]) crossover_mat_ph = tf.placeholder(tf.float32, [num_children, features]) mutation_val_ph = tf.placeholder(tf.float32, [num_children, features]) ``` 1. 現在，我們將計算人口`fitness`（負均方誤差），并找到表現最佳的人： ```py fitness = -tf.reduce_mean(tf.square(tf.subtract(population, truth_ph)), 1) top_vals, top_ind = tf.nn.top_k(fitness, k=pop_size) ``` 1. 為了達到結果和繪圖目的，我們還希望檢索人群中最適合的個體： ```py best_val = tf.reduce_min(top_vals) best_ind = tf.argmin(top_vals, 0) best_individual = tf.gather(population, best_ind) ``` 1. 接下來，我們對父代群體進行排序，并切斷表現最佳的個體，使其成為下一代的父代： ```py population_sorted = tf.gather(population, top_ind) parents = tf.slice(population_sorted, [0, 0], [num_parents, features]) ``` 1. 現在，我們將通過創建隨機洗牌的兩個父矩陣來創建子項。然后，我們將父矩陣乘以 1 和 0 的交叉矩陣，我們將為占位符生成每一代： ```py # Indices to shuffle-gather parents rand_parent1_ix = np.random.choice(num_parents, num_children) rand_parent2_ix = np.random.choice(num_parents, num_children) # Gather parents by shuffled indices, expand back out to pop_size too rand_parent1 = tf.gather(parents, rand_parent1_ix) rand_parent2 = tf.gather(parents, rand_parent2_ix) rand_parent1_sel = tf.multiply(rand_parent1, crossover_mat_ph) rand_parent2_sel = tf.multiply(rand_parent2, tf.subtract(1., crossover_mat_ph)) children_after_sel = tf.add(rand_parent1_sel, rand_parent2_sel) ``` 1. 最后的步驟是改變子項，我們將通過向子矩陣中的少量條目添加隨機正常量并將此矩陣連接回父族： ```py mutated_children = tf.add(children_after_sel, mutation_val_ph) # Combine children and parents into new population new_population = tf.concat(0, [parents, mutated_children]) ``` 1. 我們模型的最后一步是使用 TensorFlow 的`group()`操作將新種群分配給舊種群的變量： ```py step = tf.group(population.assign(new_population)) ``` 1. 我們現在可以初始化模型變量，如下所示： ```py init = tf.global_variables_initializer() sess.run(init) ``` 1. 最后，我們遍歷世代，重新創建隨機交叉和變異矩陣并更新每一代的人口： ```py for i in range(generations): # Create cross-over matrices for plugging in. crossover_mat = np.ones(shape=[num_children, features]) crossover_point = np.random.choice(np.arange(1, features-1, step=1), num_children) for pop_ix in range(num_children): crossover_mat[pop_ix,0:crossover_point[pop_ix]]=0\. # Generate mutation probability matrices mutation_prob_mat = np.random.uniform(size=[num_children, features]) mutation_values = np.random.normal(size=[num_children, features]) mutation_values[mutation_prob_mat >= mutation] = 0 # Run GA step feed_dict = {truth_ph: truth.reshape([1, features]), crossover_mat_ph: crossover_mat, mutation_val_ph: mutation_values} step.run(feed_dict, session=sess) best_individual_val = sess.run(best_individual, feed_dict=feed_dict) if i % 5 == 0: best_fit = sess.run(best_val, feed_dict = feed_dict) print('Generation: {}, Best Fitness (lowest MSE): {:.2}'.format(i, -best_fit)) ``` 1. 這產生以下輸出： ```py Generation: 0, Best Fitness (lowest MSE): 1.5 Generation: 5, Best Fitness (lowest MSE): 0.83 Generation: 10, Best Fitness (lowest MSE): 0.55 Generation: 185, Best Fitness (lowest MSE): 0.085 Generation: 190, Best Fitness (lowest MSE): 0.15 Generation: 195, Best Fitness (lowest MSE): 0.083 ``` ## 工作原理 在本文中，我們向您展示了如何使用 TensorFlow 運行簡單的遺傳算法。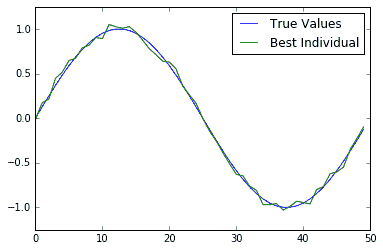為了驗證它是否有效，我們還可以在一個圖上查看最合適的個體解決方案和基本事實：  圖 4：200 代后的真實情況和最適合個體的繪圖圖。我們可以看到，最合適的個體非常接近真相 ## 更多 遺傳算法有許多變化。我們可以有兩個具有兩個不同適合度標準的父代群體（例如，最低 MSE 和平滑度）。我們可以對突變值施加限制，使其不大于 1 或小于 -1。我們可以進行許多不同的更改，這些更改會有很大差異，具體取決于我們要優化的問題。對于這個人為的問題，很容易計算出適應度，但對于大多數遺傳算法來說，計算適應度是一項艱巨的任務。例如，如果我們想使用遺傳算法來優化卷積神經網絡的架構，我們可以讓個體成為參數數組。參數可以代表每個卷積層的濾波器大小，步幅大小等。這種個體的適應性將是在通過數據集的固定量的迭代之后的分類的準確率。如果我們在這個人口中有 100 個人，我們將不得不為每一代評估 100 個不同的 CNN 模型。這在計算上非常強烈。 在使用遺傳算法解決問題之前，明智的做法是弄清楚計算個體的`fitness`需要多長時間。如果此操作耗時，遺傳算法可能不是最佳使用工具。 # 使用 K 均值聚類 TensorFlow 還可用于實現迭代聚類算法，例如 K 均值。在本文中，我們展示了在`iris`數據集上使用 K 均值的示例。 ## 準備 我們在本書中探討的幾乎所有機器學習模型都是監督模型。 TensorFlow 非常適合這些類型的問題。但是，如果我們愿意，我們也可以實現無監督的模型。例如，此秘籍將實現 K 均值聚類。 我們將實現聚類的數據集是`iris`數據集。這是一個很好的數據集的原因之一是因為我們已經知道有三種不同的目標（三種類型的鳶尾花）。這讓我們知道我們正在尋找數據中的三個不同的集群。 我們將`iris`數據集聚類為三組，然后將這些聚類的準確率與實際標簽進行比較。 ## 操作步驟 1. 首先，我們加載必要的庫。我們還從`sklearn`加載了一些 PCA 工具，以便我們可以將結果數據從四維更改為二維，以實現可視化目的： ```py import numpy as np import matplotlib.pyplot as plt import tensorflow as tf from sklearn import datasets from scipy.spatial import cKDTree from sklearn.decomposition import PCA from sklearn.preprocessing import scale ``` 1. 我們啟動圖會話，并加載`iris`數據集： ```py sess = tf.Session() iris = datasets.load_iris() num_pts = len(iris.data) num_feats = len(iris.data[0]) ``` 1. 我們現在將設置組，代，并創建圖所需的變量： ```py k=3 generations = 25 data_points = tf.Variable(iris.data) cluster_labels = tf.Variable(tf.zeros([num_pts], dtype=tf.int64)) ``` 1. 我們需要的下一個變量是每組的質心。我們將通過隨機選擇`iris`數據集的三個不同點來初始化 k-means 算法的質心： ```py rand_starts = np.array([iris.data[np.random.choice(len(iris.data))] for _ in range(k)]) centroids = tf.Variable(rand_starts) ``` 1. 現在，我們需要計算每個數據點和每個`centroids`之間的距離。我們通過將`centroids`擴展為矩陣來實現這一點，對數據點也是如此。然后我們將計算兩個矩陣之間的歐幾里德距離： ```py centroid_matrix = tf.reshape(tf.tile(centroids, [num_pts, 1]), [num_pts, k, num_feats]) point_matrix = tf.reshape(tf.tile(data_points, [1, k]), [num_pts, k, num_feats]) distances = tf.reduce_sum(tf.square(point_matrix - centroid_matrix), reduction_indices=2) ``` 1. `centroids`賦值是每個數據點最接近的`centroids`（最小距離）： ```py centroid_group = tf.argmin(distances, 1) ``` 1. 現在，我們必須計算組平均值以獲得新的質心： ```py def data_group_avg(group_ids, data): # Sum each group sum_total = tf.unsorted_segment_sum(data, group_ids, 3) # Count each group num_total = tf.unsorted_segment_sum(tf.ones_like(data), group_ids, 3) # Calculate average avg_by_group = sum_total/num_total return(avg_by_group) means = data_group_avg(centroid_group, data_points) update = tf.group(centroids.assign(means), cluster_labels.assign(centroid_group)) ``` 1. 接下來，我們初始化模型變量： ```py init = tf.global_variables_initializer() sess.run(init) ``` 1. 我們將遍歷幾代并相應地更新每個組的質心： ```py for i in range(generations): print('Calculating gen {}, out of {}.'.format(i, generations)) _, centroid_group_count = sess.run([update, centroid_group]) group_count = [] for ix in range(k): group_count.append(np.sum(centroid_group_count==ix)) print('Group counts: {}'.format(group_count)) ``` 1. 這產生以下輸出： ```py Calculating gen 0, out of 25\. Group counts: [50, 28, 72] Calculating gen 1, out of 25\. Group counts: [50, 35, 65] Calculating gen 23, out of 25\. Group counts: [50, 38, 62] Calculating gen 24, out of 25\. Group counts: [50, 38, 62] ``` 1. 為了驗證我們的聚類，我們可以使用聚類進行預測。我們現在看到有多少數據點位于相同鳶尾種類的相似簇中： ```py [centers, assignments] = sess.run([centroids, cluster_labels]) def most_common(my_list): return(max(set(my_list), key=my_list.count)) label0 = most_common(list(assignments[0:50])) label1 = most_common(list(assignments[50:100])) label2 = most_common(list(assignments[100:150])) group0_count = np.sum(assignments[0:50]==label0) group1_count = np.sum(assignments[50:100]==label1) group2_count = np.sum(assignments[100:150]==label2) accuracy = (group0_count + group1_count + group2_count)/150\. print('Accuracy: {:.2}'.format(accuracy)) ``` 1. 這產生以下輸出： ```py Accuracy: 0.89 ``` 1. 為了直觀地看到我們的分組，如果它們確實已經分離出`iris`物種，我們將使用 PCA 將四維轉換為二維，并繪制數據點和組。在 PCA 分解之后，我們在 x-y 值網格上創建預測，以繪制顏色圖： ```py pca_model = PCA(n_components=2) reduced_data = pca_model.fit_transform(iris.data) # Transform centers reduced_centers = pca_model.transform(centers) # Step size of mesh for plotting h = .02 x_min, x_max = reduced_data[:, 0].min() - 1, reduced_data[:, 0].max() + 1 y_min, y_max = reduced_data[:, 1].min() - 1, reduced_data[:, 1].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) # Get k-means classifications for the grid points xx_pt = list(xx.ravel()) yy_pt = list(yy.ravel()) xy_pts = np.array([[x,y] for x,y in zip(xx_pt, yy_pt)]) mytree = cKDTree(reduced_centers) dist, indexes = mytree.query(xy_pts) indexes = indexes.reshape(xx.shape) ``` 1. 并且，這里是`matplotlib`代碼將我們的發現結合在一個繪圖上。這個密碼的繪圖部分很大程度上改編自 [scikit-learn](http://scikit-learn.org/) [文檔網站上的演示](http://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_digits.html)： ```py plt.clf() plt.imshow(indexes, interpolation='nearest', extent=(xx.min(), xx.max(), yy.min(), yy.max()), cmap=plt.cm.Paired, aspect='auto', origin='lower') # Plot each of the true iris data groups symbols = ['o', '^', 'D'] label_name = ['Setosa', 'Versicolour', 'Virginica'] for i in range(3): temp_group = reduced_data[(i*50):(50)*(i+1)] plt.plot(temp_group[:, 0], temp_group[:, 1], symbols[i], markersize=10, label=label_name[i]) # Plot the centroids as a white X plt.scatter(reduced_centers[:, 0], reduced_centers[:, 1], marker='x', s=169, linewidths=3, color='w', zorder=10) plt.title('K-means clustering on Iris Datasets' 'Centroids are marked with white cross') plt.xlim(x_min, x_max) plt.ylim(y_min, y_max) plt.legend(loc='lower right') plt.show() ``` 這個繪圖代碼將向我們展示三個類，三個類的預測空間以及每個組的質心：  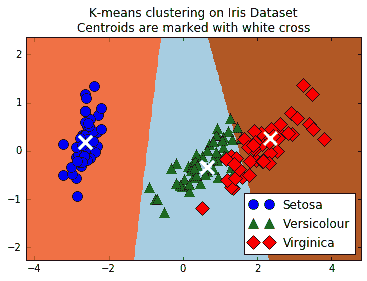圖 5：顯示 K 均值的無監督分類算法的屏幕截圖；可以用來將三種鳶尾花種組合在一起。三個 K 均值組是三個陰影區域，三個不同的點（圓，三角形和菱形）是三個真正的物種分類 ## 更多 對于此秘籍，我們使用 TensorFlow 將`iris`數據集聚類為三組。然后，我們計算了落入相似組的數據點的百分比（89%），并繪制了所得 K 均值組的圖。由于 K 均值作為分類算法是局部線性的（線性分離器向上），因此很難學習雜色鳶尾和弗吉尼亞鳶尾之間的天然非線性邊界。但是，一個優點是 K 均值算法根本不需要標記數據來執行。 # 求解常微分方程組 TensorFlow 可用于許多算法實現和過程。 TensorFlow 多功能性的一個很好的例子是實現 ODE 求解器。以數字方式求解 ODE 是一種迭代過程，可以在計算圖中輕松描述。對于這個秘籍，我們將解決 Lotka-Volterra 捕食者 - 獵物系統。 ## 準備 該秘籍將說明如何求解常微分方程（ODE）系統。我們可以使用與前兩節類似的方法來更新值，因為我們迭代并解決 ODE 系統。 我們將考慮的 ODE 系統是著名的 Lotka-Volterra 捕食者 - 獵物系統。該系統顯示了捕食者 - 食餌系統如何在給定特定參數的情況下振蕩。 Lotka-Volterra 系統于 1920 年在一篇論文中發表（參見圖 1，標量值，我們的斜率估計，在張量板中可視化）。我們將使用類似的參數來表明可以發生振蕩系統。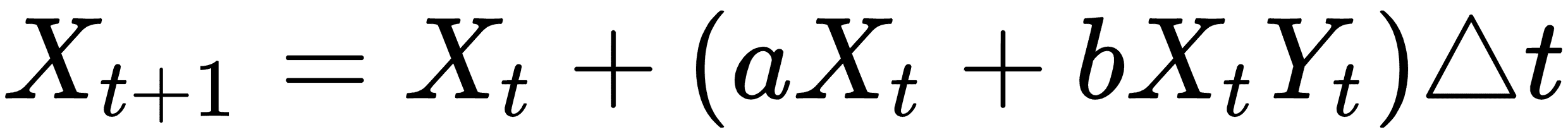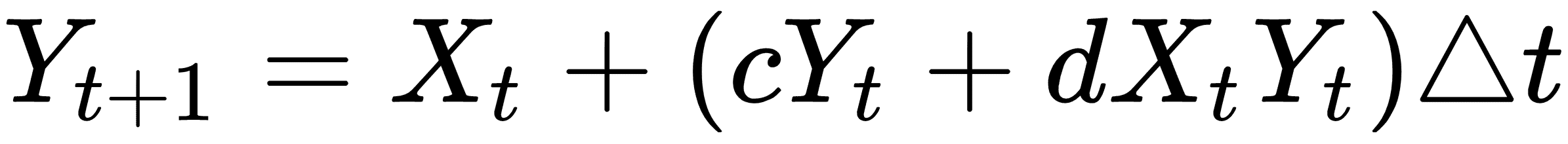這是以數學上離散的方式表示的系統：   在這里，`X`是獵物，`Y`將成為捕食者。我們通過`a`，`b`，`c`和`d`的值來確定哪個是獵物，哪個是捕食者：對于獵物，`a > 0`，`b < 0`和捕食者，`c < 0`，`d > 0`。我們將在 TensorFlow 解決方案中將此離散版本實現到系統中。 ## 操作步驟 1. 我們首先加載庫并啟動圖會話： ```py import matplotlib.pyplot as plt import tensorflow as tf sess = tf.Session() ``` 1. 然后我們在圖中聲明我們的常量和變量： ```py x_initial = tf.constant(1.0) y_initial = tf.constant(1.0) X_t1 = tf.Variable(x_initial) Y_t1 = tf.Variable(y_initial) # Make the placeholders t_delta = tf.placeholder(tf.float32, shape=()) a = tf.placeholder(tf.float32, shape=()) b = tf.placeholder(tf.float32, shape=()) c = tf.placeholder(tf.float32, shape=()) d = tf.placeholder(tf.float32, shape=()) ``` 1. 接下來，我們將實現先前引入的離散系統，然后更新`X`和`Y`群體： ```py X_t2 = X_t1 + (a * X_t1 + b * X_t1 * Y_t1) * t_delta Y_t2 = Y_t1 + (c * Y_t1 + d * X_t1 * Y_t1) * t_delta # Update to New Population step = tf.group( X_t1.assign(X_t2), Y_t1.assign(Y_t2)) ``` 1. 我們現在初始化圖并運行離散 ODE 系統，并使用特定參數來說明循環行為： ```py init = tf.global_variables_initializer() sess.run(init) # Run the ODE prey_values = [] predator_values = [] for i in range(1000): # Step simulation (using constants for a known cyclic solution) step.run({a: (2./3.), b: (-4./3.), c: -1.0, d: 1.0, t_delta: 0.01}, session=sess) # Store each outcome temp_prey, temp_pred = sess.run([X_t1, Y_t1]) prey_values.append(temp_prey) predator_values.append(temp_pred) ``` A steady state (and cyclic) solution to this specific system, the Lotka-Volterra equations, very much depends on specific parameters and population values. We encourage the reader to try different parameters and values to see what can happen. 1. 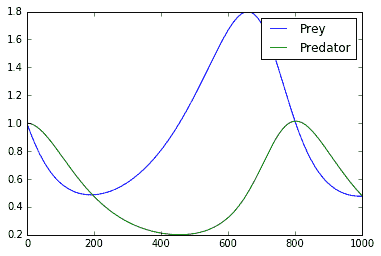現在，我們可以繪制捕食者和獵物的值： ```py plt.plot(prey_values, label="Prey") plt.plot(predator_values, label="Predator") plt.legend(loc='upper right') plt.show() ``` 這個繪圖代碼將生成一個屏幕截圖，顯示掠食者和獵物的振蕩種群：  圖 6：在這里，我們繪制 ODE 解決方案的捕食者和獵物值。事實上，我們可以看到周期確實發生了 ## 工作原理 我們使用 TensorFlow 逐步求解 ODE 系統的離散版本。對于特定參數，我們看到捕食者 - 食餌系統確實可以具有循環解。這在我們的系統生物學上是有意義的，因為如果有太多的捕食者，獵物開始死亡，然后掠食者的食物就會減少，所以他們會死掉，等等。 ## 另見 [Lotka，A.J.，關于有機系統中某些節奏關系的分析性說明](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1084562/)。 # 使用隨機森林 隨機森林算法建立在隨機選擇的觀察和/或隨機選擇的特征上的聚合決策樹上。我們不會介紹如何訓練決策樹，但會顯示有些類型的隨機森林可以使用梯度提升訓練，TensorFlow 可以為我們計算。 ## 準備 基于樹的算法傳統上是非平滑的，因為它們基于對數據進行分區以最小化目標輸出中的方差。非光滑方法不適合基于梯度的方法。 TensorFlow 依賴于以下事實：模型中使用的函數是平滑的，并且它自動計算如何更改模型參數以最小化函數損失。 TensorFlow 繞過這個障礙的方式是對決策邊界進行平滑逼近。可以使用 softmax 函數或類似形狀函數來近似決策邊界。 決策樹將通過生成規則在數據集上提供硬拆分，例如，如果`x &gt; 0.5`，則移動到樹的這個分支....這告訴我們整個數據子集將組合在一起或拆分，取決于`x`的值。這個的平滑近似處理概率而不是整個分裂。這意味著數據集的每次觀察都有可能存在于樹的每個末端節點中。下圖比較傳統決策樹和概率決策樹，可以更好地說明這些差異。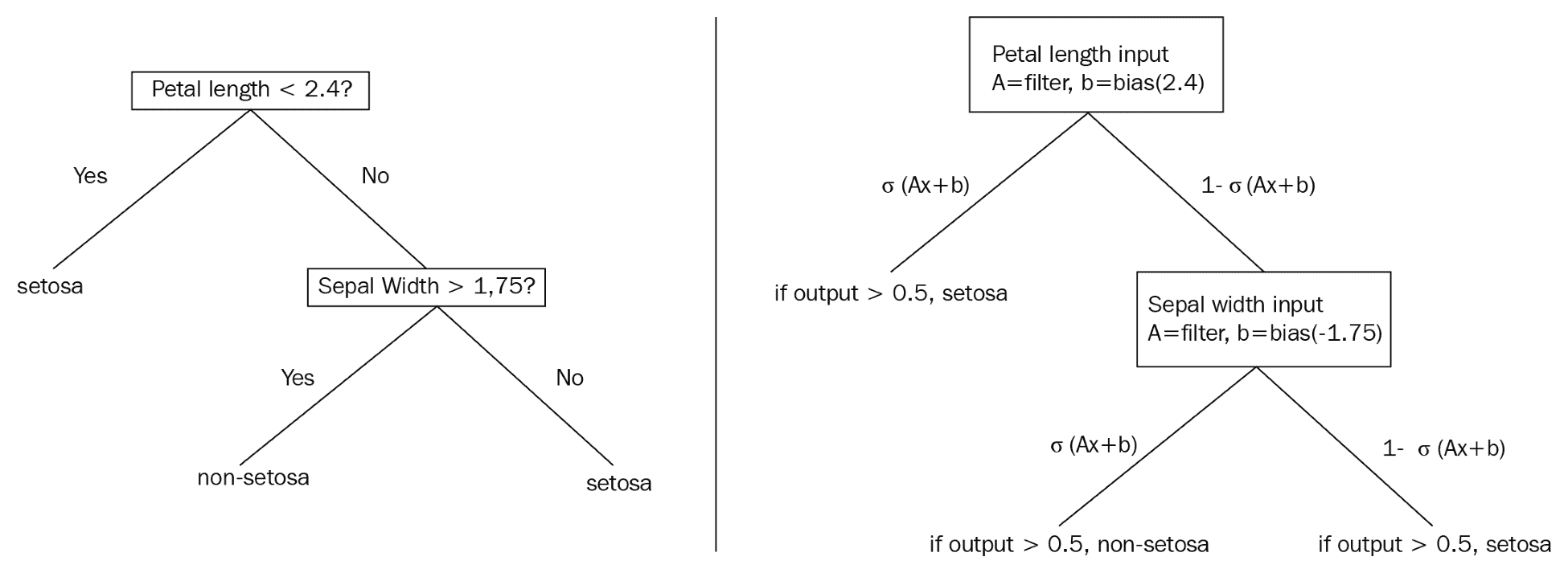 下圖說明了兩個示例決策樹之間的區別：  This diagram illustrates a standard decision tree (left) which is non-differentiable, and a smooth decision tree (right), which illustrates the usage of sigmoid functions to develop probabilities of an observation appearing in a labeled leaf or end-node. > 我們選擇不詳細介紹函數的可微性，連續性和平滑性。本節的目的是提供關于如何通過可微分模型近似非可微分模型的直觀描述。有關更多數學詳細信息，我們建議讀者查看本秘籍末尾的“另見”部分。 ## 操作步驟 TensorFlow 包含了一些我們將依賴于此秘籍的默認模型估計函數。有兩個主要的梯度提升模型，回歸樹和分類樹。對于此示例，我們將使用回歸樹來預測[波士頓房價數據集](https://www.cs.toronto.edu/~delve/data/boston/bostonDetail.html)。 1. 首先，我們加載必要的庫： ```py import numpy as np import tensorflow as tf from keras.datasets import boston_housing from tensorflow.python.framework import ops ops.reset_default_graph() ``` 1. 接下來，我們從 TensorFlow 估計器庫中設置我們將要使用的模型。在這里，我們將使用`BoostedTreesRegressor`模型，該模型用于使用梯度提升樹進行回歸： ```py regression_classifier = tf.estimator.BoostedTreesRegressor ``` > 或者，對于二分類問題，讀者可以使用估計器`BoostedTreesClassifier`。目前不支持多類別分類，盡管它將來會在路線圖上。 1. 現在，我們可以使用 Keras 數據導入函數將波士頓住房價格數據集加載到一行中，如下所示： ```py (x_train, y_train), (x_test, y_test) = boston_housing.load_data() ``` 1. 在這里，我們可以設置一些模型參數；批量大小是一次訓練的訓練觀測數量，我們將訓練`500`迭代，梯度提升森林將有`100`樹，每棵樹的最大深度（分裂數）為`6`。 ```py # Batch size batch_size = 32 # Number of training steps train_steps = 500 # Number of trees in our 'forest' n_trees = 100 # Maximum depth of any tree in forest max_depth = 6 ``` 1. TensorFlow 提供的模型估計器需要輸入函數。我們將為估計器函數創建數據輸入函數。但首先，我們需要將數據放入正確標記的`numpy`數組格式的字典中。這些在 TensorFlow 中稱為特征列。純數字列尚不支持，因此我們將數字列放入自動存儲桶中，如下所示：（a）二元特征將具有兩個存儲桶，（b）其他連續數字特征將被劃分為 5 個存儲桶。 ```py binary_split_cols = ['CHAS', 'RAD'] col_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT'] X_dtrain = {col: x_train[:, ix] for ix, col in enumerate(col_names)} X_dtest = {col: x_test[:, ix] for ix, col in enumerate(col_names)} # Create feature columns! feature_cols = [] for ix, column in enumerate(x_train.T): col_name = col_names[ix] # Create binary split feature if col_name in binary_split_cols: # To create 2 buckets, need 1 boundary - the mean bucket_boundaries = [column.mean()] numeric_feature = tf.feature_column.numeric_column(col_name) final_feature = tf.feature_column.bucketized_column(source_column=numeric_feature, boundaries=bucket_boundaries) # Create bucketed feature else: # To create 5 buckets, need 4 boundaries bucket_boundaries = list(np.linspace(column.min() * 1.1, column.max() * 0.9, 4)) numeric_feature = tf.feature_column.numeric_column(col_name) final_feature = tf.feature_column.bucketized_column(source_column=numeric_feature, boundaries=bucket_boundaries) # Add feature to feature_col list feature_cols.append(final_feature) ``` > 將輸入函數的`shuffle`選項設置為`True`進行訓練，`False`進行測試是個好主意。我們想在每個周期改變`X`和`Y`訓練集，但不是在測試期間。 1. 我們現在使用 TensorFlow 估計器中輸入庫的`numpy`輸入函數聲明我們的數據輸入函數。我們將指定我們創建的訓練觀察詞典和一組`y`目標。 ```py input_fun = tf.estimator.inputs.numpy_input_fn(X_dtrain, y=y_train, batch_size=batch_size, num_epochs=10, shuffle=True) ``` 1. 現在，我們定義我們的模型并開始訓練： ```py model = regression_classifier(feature_columns=feature_cols, n_trees=n_trees, max_depth=max_depth, learning_rate=0.25, n_batches_per_layer=batch_size) model.train(input_fn=input_fun, steps=train_steps) ``` 1. 在訓練期間，我們應該看到類似的輸出如下： ```py INFO:tensorflow:Using default config. WARNING:tensorflow:Using temporary folder as model directory: /tmp/tmpqxyd62cu INFO:tensorflow:Using config: {'_model_dir': '/tmp/tmpqxyd62cu', '_tf_random_seed': None, '_save_summary_steps': 100, '_save_checkpoints_steps': None, '_save_checkpoints_secs': 600, '_session_config': None, '_keep_checkpoint_max': 5, '_keep_checkpoint_every_n_hours': 10000, '_log_step_count_steps': 100, '_train_distribute': None, '_device_fn': None, '_service': None, '_cluster_spec': <tensorflow.python.training.server_lib.ClusterSpec object at 0x7f43129d77b8>, '_task_type': 'worker', '_task_id': 0, '_global_id_in_cluster': 0, '_master': '', '_evaluation_master': '', '_is_chief': True, '_num_ps_replicas': 0, '_num_worker_replicas': 1} INFO:tensorflow:Calling model_fn. INFO:tensorflow:Done calling model_fn. INFO:tensorflow:Create CheckpointSaverHook. INFO:tensorflow:Graph was finalized. INFO:tensorflow:Running local_init_op. INFO:tensorflow:Done running local_init_op. INFO:tensorflow:Saving checkpoints for 0 into /tmp/tmpqxyd62cu/model.ckpt. INFO:tensorflow:loss = 691.09814, step = 1 INFO:tensorflow:global_step/sec: 587.923 INFO:tensorflow:loss = 178.62021, step = 101 (0.171 sec) INFO:tensorflow:Saving checkpoints for 127 into /tmp/tmpqxyd62cu/model.ckpt. INFO:tensorflow:Loss for final step: 37.436565. Out[190]: <tensorflow.python.estimator.canned.boosted_trees.BoostedTreesRegressor at 0x7f43129d7470> ``` 1. 為了評估我們的模型，我們為測試數據創建了另一個輸入函數，并獲得每個測試數據點的預測。以下是獲取預測并打印平均絕對誤差（MAE）的代碼： ```py p_input_fun = tf.estimator.inputs.numpy_input_fn(X_dtest, y=y_test, batch_size=batch_size, num_epochs=1, shuffle=False) # Get predictions predictions = list(model.predict(input_fn=p_input_fun)) final_preds = [pred['predictions'][0] for pred in predictions] # Get accuracy (mean absolute error, MAE) mae = np.mean([np.abs((actual - predicted) / predicted) for actual, predicted in zip(y_test, final_preds)]) print('Mean Abs Err on test set: {}'.format(acc)) ``` 1. 其中以`0.71`打印出誤差。請注意，由于隨機播放的隨機性，讀者可能會得到略微不同的結果。為了提高準確率，我們可以考慮增加數字周期或引入更低的學習率甚至是某種類型的衰減學習率（指數或線性）： ```py Mean Abs Err on test set: 0.7111111111111111 ``` ## 工作原理 在本文中，我們將說明如何使用 TensorFlow 估計器和 TensorFlow 提供的數據輸入函數。這些函數非常強大，不僅使我們的 TensorFlow 代碼更短，更易讀，而且還提高了算法的效率，減少了創建和測試算法所需的開發時間。 ## 另見 有關決策樹，隨機森林，梯度提升森林以及可微分性，平滑性和連續性背后的數學的更多參考，我們鼓勵讀者閱讀以下參考文獻。 1. 決策樹教程。來自[伯克利的機器學習速成課程](https://ml.berkeley.edu/blog/2017/12/26/tutorial-5/)。 2. [隨機森林 python 教程，克里斯阿爾邦](https://chrisalbon.com/machine_learning/trees_and_forests/random_forest_classifier_example/) 3. 關于凸函數的精美 PDF 演示，它們如何用于機器學習，以及平滑度，可微性和連續性之間的差異。作者為弗朗西斯巴赫。最后還有[大約 6 頁有用的參考文獻](https://www.di.ens.fr/~fbach/gradsto_allerton.pdf)，讀者可能會覺得有用。 4. 關于軟決策樹的文章：[將神經網絡提煉為軟決策樹，Frosst 和 Hinton，2017](https://cex.inf.unibz.it/resources/Frosst+Hinton-CExAIIA_2017.pdf)。 5. [TensorFlow 實現的一個神經樹](https://github.com/benoitdescamps/Neural-Tree)。作者：Benoit Deschamps。 # 使用 TensorFlow 和 Keras TensorFlow 非常適合為程序員提供的靈活性和強大功能。這樣做的一個缺點是原型模型和迭代各種測試對程序員來說可能很麻煩。 Keras 是深度學習庫的包裝器，可以更輕松地處理模型的各個方面并使編程更容易。在這里，我們選擇在 TensorFlow 之上使用 Keras。事實上，使用帶有 TensorFlow 后端的 Keras 非常受歡迎，TensorFlow 中有一個 Keras 庫。對于這個秘籍，我們將使用該 TensorFlow 庫在 MNIST 數據集上進行完全連接的神經網絡和簡單的 CNN 圖像網絡。 ## 準備 對于這個秘籍，我們將使用駐留在 TensorFlow 內部的 Keras 函數。 [Keras](https://keras.io/) 已經是一個可以安裝的獨立 python 庫了。如果您選擇使用純 Keras 路線，則必須為 Keras 選擇后端（如 TensorFlow）。 在本文中，我們將在 MNIST 圖像識別數據集上執行兩個單獨的模型。第一個是直接完全連接的神經網絡，而第二個是從第 8 章第 2 節“實現簡單的 CNN”復制我們的 CNN 網絡。 ## 操作步驟 1. 我們將首先為腳本加載必要的庫。 ```py import tensorflow as tf from sklearn.preprocessing import MultiLabelBinarizer from keras.utils import to_categorical from tensorflow import keras from tensorflow.python.framework import ops ops.reset_default_graph() # Load MNIST data from tensorflow.examples.tutorials.mnist import input_data ``` 1. 我們可以在 TensorFlow 中使用提供的 MNIST 數據導入函數加載庫。雖然原始 MNIST 圖像是 28 像素乘 28 像素，但導入的數據是它們的扁平版本，其中每個觀察是 0 到 1 之間的 784 個灰度點的行。y 標簽作為 0 到 9 之間的整數導入。 ```py mnist = input_data.read_data_sets("MNIST_data/") x_train = mnist.train.images x_test = mnist.test.images y_train = mnist.train.labels y_test = mnist.test.labels y_train = [[i] for i in y_train] y_test = [[i] for i in y_test] ``` 1. 我們現在將使用 scikit-learn 的`MultiLabelBinarizer()`函數將目標整數轉換為單熱編碼向量，如下所示： ```py one_hot = MultiLabelBinarizer() y_train = one_hot.fit_transform(y_train) y_test = one_hot.transform(y_test) ``` 1. 我們將創建一個三層完全連接的神經網絡，其中包含 32，16 和 10 個相應的隱藏節點。然后最終輸出的大小為 10（每個數字一個）。我們使用以下代碼創建此網絡： ```py # We start with a 'sequential' model type (connecting layers together) model = keras.Sequential() # Adds a densely-connected layer with 32 units to the model, followed by an ReLU activation. model.add(keras.layers.Dense(32, activation='relu')) # Adds a densely-connected layer with 16 units to the model, followed by an ReLU activation. model.add(keras.layers.Dense(16, activation='relu')) # Add a softmax layer with 10 output units: model.add(keras.layers.Dense(10, activation='softmax')) ``` 1. 為了訓練模型，我們接下來要做的就是使用適當的參數調用`compile()`方法。我們需要的參數是優化函數和損失類型。但我們也想記錄模型的準確率，因此度量列表包括`accuracy`參數。 ```py model.compile(optimizer=tf.train.AdamOptimizer(0.001), loss='categorical_crossentropy', metrics=['accuracy']) ``` 1. 這將使輸出應類似于以下內容： ```py Epoch 1/5 64/55000 [..............................] - ETA: 1:44 - loss: 2.3504 - acc: 0.0625 3776/55000 [=>............................] - ETA: 2s - loss: 1.7904 - acc: 0.3676 ... 47104/55000 [========================>.....] - ETA: 0s - loss: 0.1337 - acc: 0.9615 50880/55000 [==========================>...] - ETA: 0s - loss: 0.1336 - acc: 0.9617 55000/55000 [==============================] - 1s 13us/step - loss: 0.1335 - acc: 0.9615 Out[]: <tensorflow.python.keras.callbacks.History at 0x7f5768a40da0> ``` > 要配置均方誤差損失的回歸模型，我們將使用模型編譯，如下所示：`model.compile(optimizer=tf.train.AdamOptimizer(0.01), loss='mse', metrics=['mae'])` 1. 接下來，我們將看到如何實現具有兩個卷積層的 CNN 模型，其具有最大池，全部后面是完全連接的層。首先，我們必須將平面圖像重塑為 2D 圖像，并將 y 目標轉換為 numpy 數組，如下所示：00 ```py x_train = x_tra0in.reshape(x_train.shape[0], 28, 28, 1) x_test = x_test.reshape(x_test.shape[0], 28, 28, 1) input_shape = (28, 28, 1) num_classes = 10 # Categorize y targets y_test = to_categorical(mnist.test.labels) y_train = to_categorical(mnist.train.labels) ``` 1. 我們將像以前一樣以類似的順序層方法創建 CNN。這次我們將使用`Conv2D()`，`MaxPooling2D()`和`Dense()` Keras 函數創建我們的 CNN 模型，如下所示： ```py cnn_model = keras.Sequential() # First convolution layer cnn_model.add(keras.layers.Conv2D(25, kernel_size=(4, 4), strides=(1, 1), activation='relu', input_shape=input_shape)) # Max pooling cnn_model.add(keras.layers.MaxPooling2D(pool_size=(2, 2), strides=(2, 2))) # Second convolution layer cnn_model.add(keras.layers.Conv2D(50, kernel_size=(5, 5), strides=(1, 1), activation='relu')) # Max pooling cnn_model.add(keras.layers.MaxPooling2D(pool_size=(2, 2), strides=(2, 2))) # Flatten for dense (fully connected) layer cnn_model.add(keras.layers.Flatten()) # Add dense (fully connected) layer cnn_model.add(keras.layers.Dense(num_classes, activation='softmax')) ``` 1. 接下來，我們將通過選擇優化和損失函數來編譯我們的模型。 ```py cnn_model.compile(optimizer=tf.train.AdamOptimizer(0.001), loss='categorical_crossentropy', metrics=['accuracy']) ``` 1. Keras 還允許我們將函數插入到名為`Callback`的訓練代碼中。回調是在代碼中的某些時間執行的函數，可用于執行各種函數。有許多預制回調，可以保存模型，在特定標準下停止訓練，記錄值等等。有關各種選項的更多信息，請參閱[此鏈接](https://keras.io/callbacks/)。為了說明如何制作我們自己的自定義回調并顯示它們如何工作，我們將創建一個名為`RecordAccuracy()`的回調，它是一個 Keras `Callback`類，并將在每個周期的末尾存儲精度，如下所示： ```py class RecordAccuracy(keras.callbacks.Callback): def on_train_begin(self, logs={}): self.acc = [] def on_epoch_end(self, batch, logs={}): self.acc.append(logs.get('acc')) accuracy = RecordAccuracy() ``` 1. 接下來，我們將使用`fit()`方法訓練我們的 CNN 模型。這里我們將提供`validation_data`和`callbacks`如下： ```py cnn_model.fit(x_train, y_train, batch_size=64, epochs=3, validation_data=(x_test, y_test), callbacks=[accuracy]) print(accuracy.acc) ``` 1. 此訓練將產生類似的輸出，如下所示： ```py Train on 55000 samples, validate on 64 samples Epoch 1/3 64/55000 [..............................] - ETA: 2:59 - loss: 2.2805 - acc: 0.0625 192/55000 [>.............................] - ETA: 1:14 - loss: 2.2729 - acc: 0.1302\ ... 54848/55000 [============================>.] - ETA: 0s - loss: 0.0603 - acc: 0.9816 54976/55000 [============================>.] - ETA: 0s - loss: 0.0603 - acc: 0.9816 55000/55000 [==============================] - 26s 469us/step - loss: 0.0604 - acc: 0.9816 - val_loss: 0.0139 - val_acc: 1.0000 Out[]: <tensorflow.python.keras.callbacks.History at 0x7f69494c7780> [0.9414363636450334, 0.9815818181731484, 0.9998980778226293] ``` ## 工作原理 在這個秘籍中，我們展示了 Keras 的簡潔創建和訓練模型。您可以自動處理變量類型，維度和數據攝取的許多復雜細節。雖然這可以讓人放心，但我們應該意識到，如果我們掩蓋太多模型細節，我們可能無意中實現了錯誤的模型。 ## 另見 有關 Keras 的更多信息，建議讀者查看以下資源： * [Keras 官方文檔](https://keras.io/) * [TensorFlow Keras 教程](https://www.tensorflow.org/guide/keras) * [“Keras 簡介”，Francois Chollet 在斯坦福大學的客座講座（幻燈片中的 PDF 格式）]https://web.stanford.edu/class/cs20si/lectures/march9guestlecture.pdf