# 二、深度學習基礎 本章從深度學習真正含義的最基本基礎開始，然后深入到圍繞神經網絡的其他基本概念和術語，深入探討了深度學習的基本知識。 將向讀者概述神經網絡的基本構建模塊，以及如何訓練深度神經網絡。 涵蓋模型訓練的概念，包括激活函數，損失函數，反向傳播和超參數調整策略。 這些基礎概念對于正在嘗試深度神經網絡模型的初學者和經驗豐富的數據科學家都將有很大的幫助。 我們特別關注如何建立具有 GPU 支持的強大的基于云的深度學習環境，以及設置內部深度學習環境的技巧。 對于希望自己構建大規模深度學習模型的讀者來說，這將非常有用。 本章將涵蓋以下主題： * 什么是深度學習？ * 深度學習基礎 * 建立具有 GPU 支持的強大的基于云的深度學習環境 * 建立具有 GPU 支持的強大的本地深度學習環境 * 神經網絡基礎 # 什么是深度學習？ 在**機器學習**（**ML**）中，我們嘗試自動發現用于將輸入數據映射到所需輸出的規則。 在此過程中，創建適當的數據表示形式非常重要。 例如，如果我們要創建一種將電子郵件分類為垃圾郵件/火腿的算法，則需要用數字表示電子郵件數據。 一個簡單的表示形式可以是二元向量，其中每個組件從預定義的單詞表中描述單詞的存在與否。 同樣，這些表示是與任務相關的，也就是說，表示可能會根據我們希望 ML 算法執行的最終任務而有所不同。 在前面的電子郵件示例中，如果我們要檢測電子郵件中的情感，則不必標識垃圾郵件/火腿，而更有用的數據表示形式可以是二元向量，其中預定義詞匯表由具有正極性或負極性的單詞組成。 大多數 ML 算法（例如隨機森林和邏輯回歸）的成功應用取決于數據表示的質量。 我們如何獲得這些表示？ 通常，這些表示是人為制作的特征，通過做出一些明智的猜測來進行迭代設計。 此步驟稱為**特征工程**，是大多數 ML 算法中的關鍵步驟之一。 **支持向量機**（**SVM**）或一般的內核方法，試圖通過將數據的手工表示轉換為更高維度的空間來創建更相關的數據表示，使得使用分類或回歸來解決 ML 任務變得容易。 但是，SVM 很難擴展到非常大的數據集，并且在諸如圖像分類和語音識別等問題上并不成功。 諸如隨機森林和**梯度提升機**（**GBMs**）之類的集合模型創建了一組弱模型，這些模型專門用于很好地完成小任務，然后將這些弱模型以一些方式組合來產生最終輸出。 當我們有非常大的輸入尺寸時，它們工作得很好，而創建手工制作的特征是非常耗時的步驟。 總而言之，所有前面提到的 ML 方法都以淺淺的數據表示形式工作，其中涉及通過一組手工制作的特征進行數據表示，然后進行一些非線性轉換。 深度學習是 ML 的一個子字段，在其中創建數據的分層表示。 層次結構的較高級別由較低級別的表示形式組成。 更重要的是，通過完全自動化 ML 中最關鍵的步驟（稱為**特征工程**），可以從數據中自動學習這種表示層次。 在多個抽象級別上自動學習特征允許系統直接從數據中學習輸入到輸出的復雜表示形式，而無需完全依賴于人工制作的特征。 深度學習模型實際上是具有多個隱藏層的神經網絡，它可以幫助創建輸入數據的分層層次表示。 之所以稱為*深度*，是因為我們最終使用了多個隱藏層來獲取表示。 用最簡單的術語來說，深度學習也可以稱為**分層特征工程**（當然，我們可以做更多的事情，但這是核心原理）。 深度神經網絡的一個簡單示例可以是具有多個隱藏層的**多層感知器**（**MLP**）。 下圖中考慮基于 MLP 的人臉識別系統。 它學習到的最低級別的特征是對比度的一些邊緣和圖案。 然后，下一層能夠使用那些局部對比的圖案來模仿眼睛，鼻子和嘴唇。 最后，頂層使用這些面部特征創建面部模板。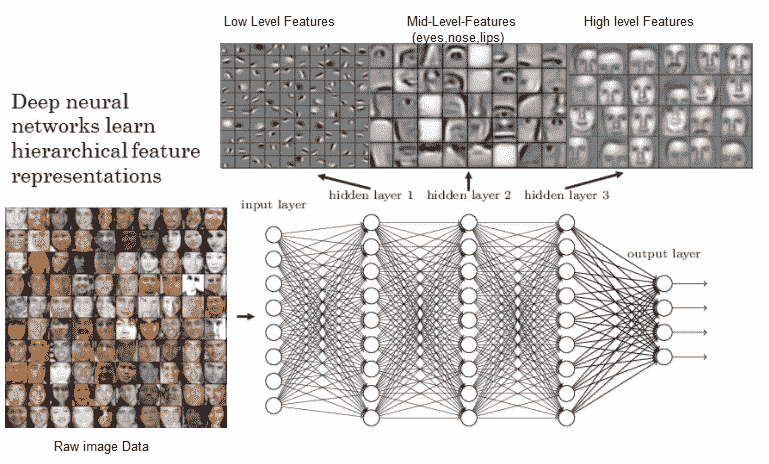 深度網絡正在組成簡單的特征，以創建越來越復雜的特征，如下圖所示：  [具有深度神經網絡的分層特征表示](https://www.rsipvision.com/exploring-deep-learning/) 為了理解深度學習，我們需要對神經網絡的構建模塊，如何訓練這些網絡以及如何將這樣的訓練算法擴展到非常大的深度網絡有一個清晰的了解。 在深入探討有關神經網絡的更多細節之前，讓我們嘗試回答一個問題：為什么現在要進行深度學習？ 神經網絡的理論，甚至是**卷積神經網絡**（**CNN**）都可以追溯到 1990 年代。 他們之所以變得越來越受歡迎的原因歸結于以下三個原因： * **高效硬件的可用性**：摩爾定律使 CPU 具有更好，更快的處理能力和計算能力。 除此之外，GPU 在大規模計算數百萬個矩陣運算中也非常有用，這是任何深度學習模型中最常見的運算。 諸如 CUDA 之類的 SDK 的可用性已幫助研究社區重寫了一些可高度并行化的作業，以在少數 GPU 上運行，從而取代了龐大的 CPU 集群。 模型訓練涉及許多小的線性代數運算，例如矩陣乘法和點積，這些運算在 CUDA 中非常有效地實現以在 GPU 中運行。 * **大型數據源的可用性和更便宜的存儲**：現在，我們可以免費訪問大量帶標簽的文本，圖像和語音訓練集。 * **用于訓練神經網絡的優化算法的進展**：傳統上，只有一種算法可用于學習神經網絡中的權重，梯度下降或**隨機梯度下降**（**SGD**）。 SGD 具有一些局限性，例如卡在局部最小值和收斂速度較慢，這些都可以通過較新的算法來克服。 我們將在后面的“神經網絡基礎知識”的后續部分中詳細討論這些算法。 # 深度學習框架 深度學習廣泛普及和采用的主要原因之一是 Python 深度學習生態系統，它由易于使用的開源深度學習框架組成。 但是，考慮到新框架如何不斷發布以及舊框架將要壽終正寢，深度學習的格局正在迅速變化。 深度學習愛好者可能知道 Theano 是由 Yoshua Bengio 領導的 [MILA](https://mila.quebec/) 創建的第一個也是最受歡迎的深度學習框架。 不幸的是，最近宣布，在 Theano 的最新版本（1.0）于 2017 年發布之后，對 Theano 的進一步開發和支持將結束。因此，了解那里可以利用哪些框架來實現和解決問題至關重要。 深度學習。 這里要記住的另一點是，幾個組織本身正在建立，獲取和啟動這些框架（通常試圖在更好的功能，更快的執行等方面相互競爭），以使每個人都受益。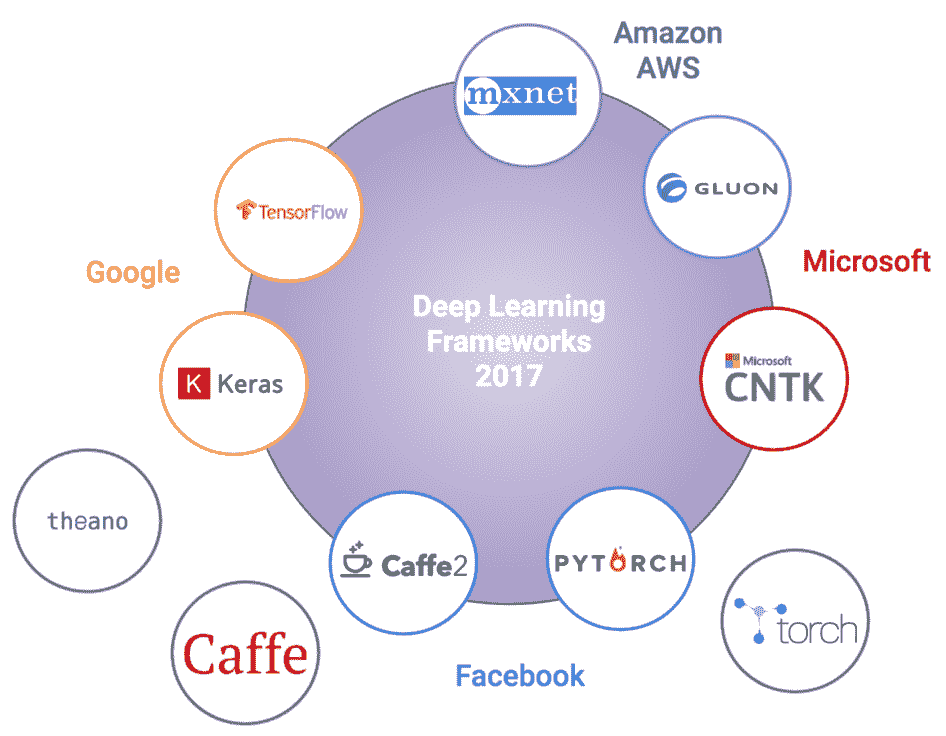 下圖展示了截至 2018 年最受歡迎的一些深度學習框架：  您還可以在[**邁向數據科學**](https://towardsdatascience.com/battle-of-the-deep-learning-frameworks-part-i-cff0e3841750)了解更多。 讓我們簡要看看一些最受歡迎的深度學習框架： * **Theano**：默認情況下，Theano 是一個低級框架，可對多維數組（現在通常稱為**張量**）進行高效的數值計算。 Theano 非常穩定，語法與 TensorFlow 非常相似。 它確實具有 GPU 支持，但功能有限，特別是如果我們要使用多個 GPU。 由于其在 1.0 之后的開發和停止支持，如果您打算將 theano 用于深度學習實現，則應格外小心。 * **TensorFlow**：這可能是最流行（或至少最流行）的深度學習框架。 它由 Google Brain 創建并于 2015 年開源，迅速吸引了 ML，深度學習研究人員，工程師和數據科學家的關注。 盡管初始發行版的表現存在問題，但它仍處于積極開發中，并且每個發行版都在不斷完善。 TensorFlow 支持基于多 CPU 和 GPU 的執行，并支持多種語言，包括 C++，Java，R 和 Python。 它僅用于支持符號編程樣式來構建深度學習模型，該模型稍微復雜一些，但是自 v1.5 起廣泛采用，它開始支持更流行且易于使用的命令式編程樣式（也稱為**立即執行**）。 TensorFlow 通常是類似于 Theano 的低級庫，但也具有利用高級 API 進行快速原型設計和開發的功能。 TensorFlow 的重要部分還包括`tf.contrib`模塊，該模塊包含各種實驗功能，包括 Keras API 本身！ * **Keras**：如果發現自己對利用底層深度學習框架來解決問題感到困惑，則可以始終依靠 Keras！ 具有不同技能的人們廣泛使用此框架，包括可能不是核心開發人員的科學家。 這是因為 Keras 提供了一個簡單，干凈且易于使用的高級 API，用于以最少的代碼構建有效的深度學習模型。 這樣做的好處是可以將其配置為在包括 theano 和 TensorFlow 在內的多個低級深度學習框架（稱為**后端**）之上運行。 可通過 [keras.io](https://keras.io/) 訪問 Keras 文檔，并且非常詳細。 * **Caffe**：這也是伯克利視覺與學習中心以 C++ （包括 Python 綁定）開發的第一個且相對較舊的深度學習框架之一。 關于 Caffe 的最好之處在于，它作為 Caffe Model Zoo 的一部分提供了許多預訓練的深度學習模型。 Facebook 最近開放了 Caffe2 的源代碼，它基于 Caffe 進行了改進，并且比其前身更易于使用。 * **PyTorch**：Torch 框架是用 Lua 編寫的，非常靈活和快速，通常可以帶來巨大的表現提升。 PyTorch 是用于構建深度學習模型的基于 Python 的框架，它從 Torch 汲取了靈感。 它不僅是 Torch 的擴展或 Python 包裝器，而且本身就是一個完整的框架，從而改進了 Torch 框架架構的各個方面。 這包括擺脫容器，利用模塊以及表現改進（例如內存優化）。 * **CNTK**：Cognitive Toolkit 框架已由 Microsoft 開源，并且支持 Python 和 C++ 。 語法與 Keras 非常相似，并且支持多種模型架構。 盡管不是很流行，但這是 Microsoft 內部用于其幾種認知智能功能的框架。 * **MXNet**：這是由**分布式機器學習社區**（**DMLC**）開發的，該包是非常受歡迎的 XGBoost 包的創建者。 現在這是一個官方的 Apache Incubator 項目。 MXNet 是最早支持各種語言（包括 C++，Python，R 和 Julia）以及多種操作系統（包括 Windows）的深度學習框架之一，而其他 Windows 常常會忽略該框架。 該框架非常高效且可擴展，并支持多 GPU。 因此，它已成為 Amazon 選擇的深度學習框架，并為此開發了一個高級接口，稱為 **Gluon**。 * **Gluon**：這是一個高級深度學習框架，或者說是接口，可以在 MXNet 和 CNTK 的基礎上加以利用。 Gluon 由 Amazon AWS 和 Microsoft 聯合開發，與 Keras 非常相似，可以被視為直接競爭對手。 然而，它聲稱它將隨著時間的推移支持更多的低層深度學習框架，并具有使**人工智能**（**AI**）民主化的愿景。 Gluon 提供了一個非常簡單，干凈和簡潔的 API，任何人都可以使用它以最少的代碼輕松構建深度學習架構。 * **BigDL**：將 BigDL 視為大規模的大數據深度學習！ 該框架由 Intel 開發，可以在 Apache Spark 之上利用，以在 Hadoop 集群上以分布式方式構建和運行深度學習模型，作為 Spark 程序。 它還利用非常流行的英特爾**數學內核庫**（**MKL**）來提高表現并提高表現。 上面的框架列表絕對不是深度學習框架的詳盡列表，但是應該使您對深度學習領域中的內容有個很好的了解。 隨意探索這些框架，并根據最適合您的情況選擇任何一個。 永遠記住，有些框架的學習曲線很陡峭，所以如果花時間學習和利用它們，不要灰心。 盡管每個框架都有各自的優點和缺點，但您應始終將更多的精力放在要解決的問題上，然后利用最適合解決問題的框架。 # 建立具有 GPU 支持的基于云的深度學習環境 深度學習在帶有 CPU 的標準單 PC 設置中效果很好。 但是，一旦您的數據集開始增加大小，并且模型架構開始變得更加復雜，您就需要開始考慮在強大的深度學習環境中進行投資。 主要期望是該系統可以有效地構建和訓練模型，花費較少的時間來訓練模型，并且具有容錯能力。 大多數深度學習計算本質上是數百萬個矩陣運算（數據表示為矩陣），并且可以并行進行快速計算。 事實證明，GPU 在這方面可以很好地工作。 您可以考慮建立一個強大的基于云的深度學習環境，甚至是一個內部環境。 讓我們看看如何在本節中建立一個強大的基于云的深度學習環境。 涉及的主要組件如下： * 選擇云提供商 * 設置您的虛擬服務器 * 配置您的虛擬服務器 * 安裝和更新深度學習依賴項 * 訪問您的深度學習云環境 * 在您的深度學習環境中驗證 GPU 的啟用 讓我們更詳細地研究這些組件中的每個組件，并逐步執行過程，以幫助您建立自己的深度學習環境。 # 選擇云提供商 如今，有多家云提供商的價格可承受且具有競爭力。 我們希望利用**平臺即服務**（**PaaS**）功能來管理數據，應用和基本配置。 下圖顯示了一些流行的云提供商：  受歡迎的提供商包括亞馬遜的 AWS，微軟的 Azure 和 Google 的 **Google 云平臺**（**GCP**）。 就本教程和本書而言，我們將利用 AWS。 # 設置您的虛擬服務器 您需要獲取一個 AWS 賬戶才能執行本節中的其余步驟。 如果您還沒有帳戶，請轉到[這里](https://aws.amazon.com/)創建一個帳戶。 準備就緒后，您可以登錄[這里](https://console.aws.amazon.com/ec2/v2/)來登錄您的帳戶并導航到 AWS EC2 控制面板，該工具利用了**彈性計算云**（**EC2**）服務，這是 Amazon 云計算服務的基礎。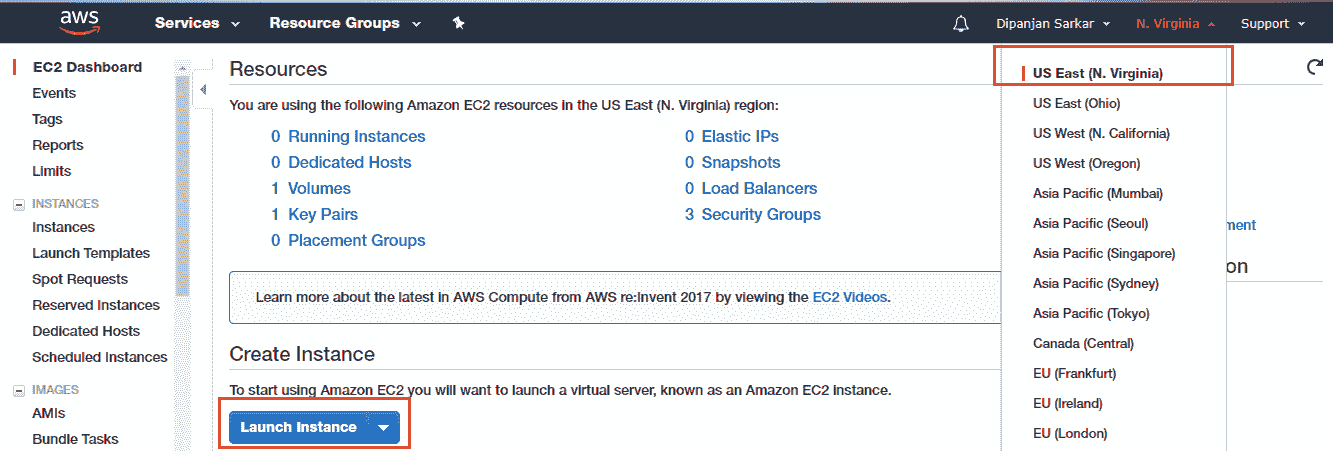 到達那里后，請記住選擇一個您選擇的區域（我通常與美國東部一起去），然后單擊“啟動實例”以啟動在云上創建新虛擬服務器的過程：  單擊啟動實例按鈕應帶您到該頁面，以選擇您自己的 **Amazon Machine Image**（**AMI**）。 通常，AMI 由構建虛擬服務器所需的各種軟件配置組成。 它包括以下內容： * 實例的根卷的模板，其中包括服務器的操作系統，應用和其他配置設置。 * 啟動許可設置，用于控制哪些 AWS 賬戶可以使用 AMI 啟動實例。 * 塊設備映射，用于指定啟動實例時要附加到實例的存儲卷。 您所有的數據都在這里！ 我們將利用專門用于深度學習的預構建 AMI，因此我們不必花時間進行額外的配置和管理。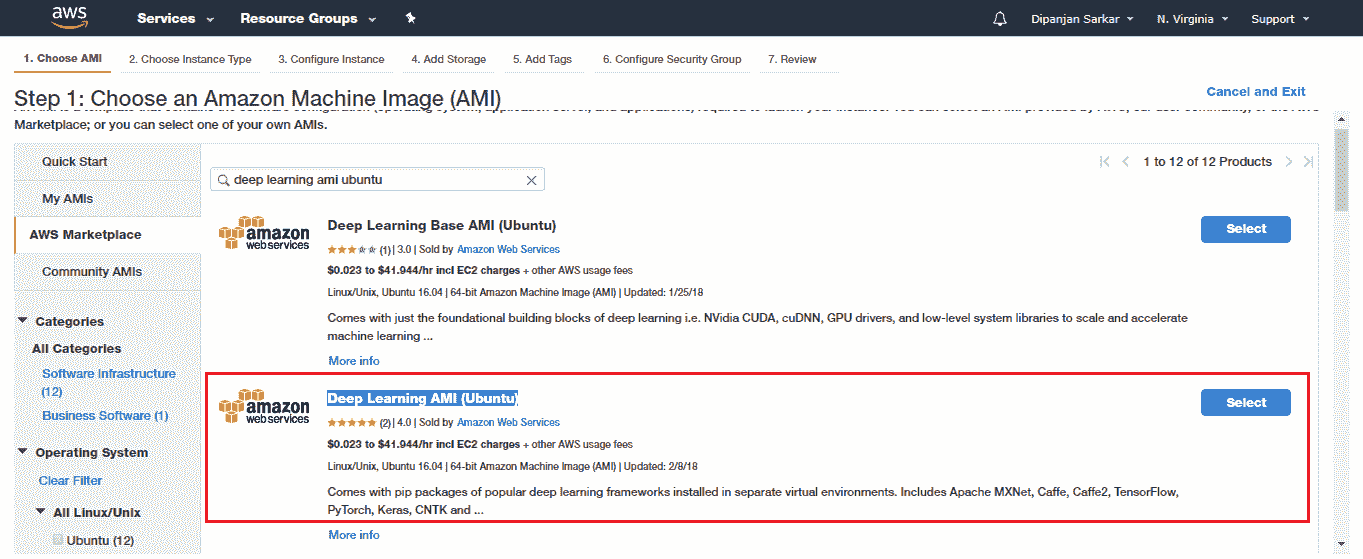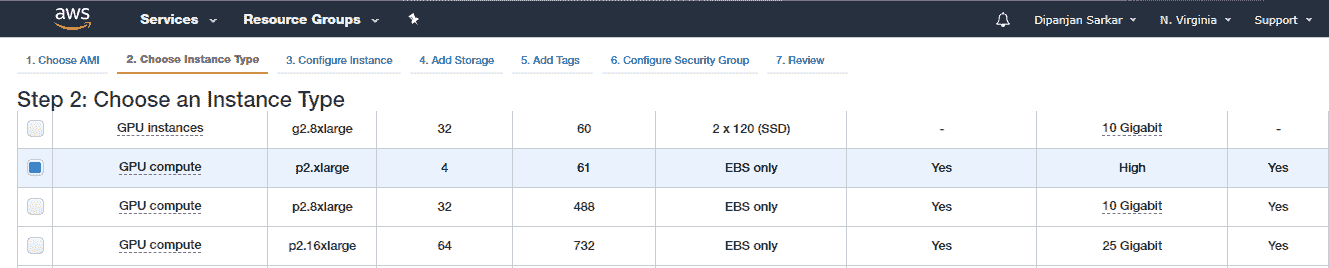 前往 AWS Marketplace 并選擇深度學習 AMI（Ubuntu）：  選擇 AMI 之后，您需要選擇實例類型。 對于支持 GPU 的深度學習，我們建議使用 p2.xlarge 實例，該實例功能強大且經濟實惠，每小時使用成本約為 0.90 美元（截至 2018 年）。 P2 實例最多可提供 16 個 NVIDIA K80 GPU，64 個 vCPU 和 732 GiB 主機內存，以及總共 192 GB 的 GPU 內存，如以下屏幕快照所示：  接下來是配置實例詳細信息。 除非希望啟動多個實例，指定子網首選項以及指定關閉行為，否則可以保留默認設置。 下一步涉及添加存儲詳細信息。 通常，您具有根卷，可以在根卷中根據需要增加其大小，并添加額外的**彈性塊存儲**（**EBS**）卷以增加磁盤空間。 然后，我們看一下是否需要添加標簽（區分大小寫和鍵值對）。 目前我們不需要這個，所以我們跳過它。 我們將重點放在配置安全組的下一步上，特別是如果您想通過利用功能強大的 Jupyter 筆記本從外部訪問深度學習設置。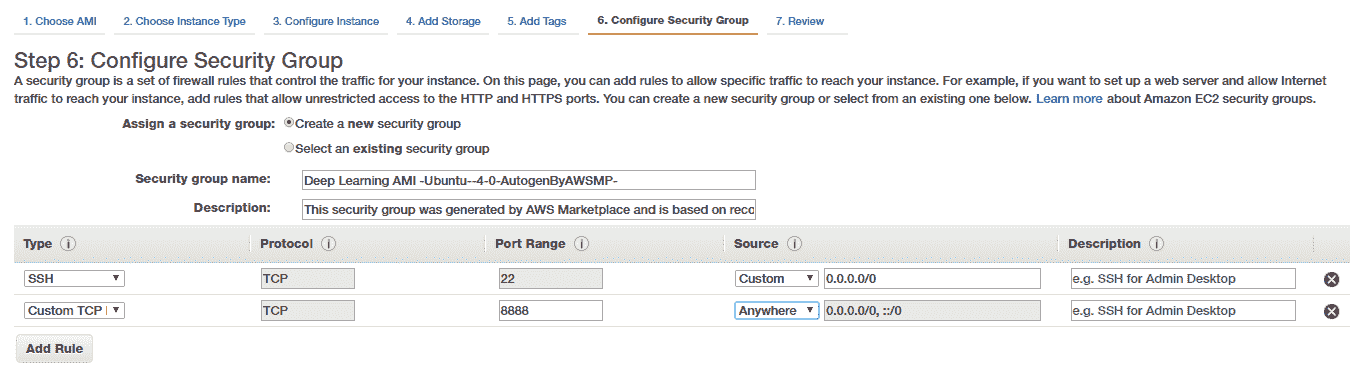 為此，我們創建一個新的安全組并創建一個 Custom TCP 規則以打開并啟用對端口`8888`的訪問，如下所示：  請注意，此規則通常允許任何 IP 監聽您實例（我們將在其中運行 Jupyter 筆記本的實例）上的端口（`8888`）。 如果需要，可以更改此設置，僅添加特定 PC 或筆記本電腦的 IP 地址，以提高安全性。 除此之外，我們稍后還將為 Jupyter 筆記本添加一個額外的密碼保護功能，以提高安全性。 最后，您將需要通過創建密鑰對（公鑰和私鑰）來啟動實例，以安全地連接到實例。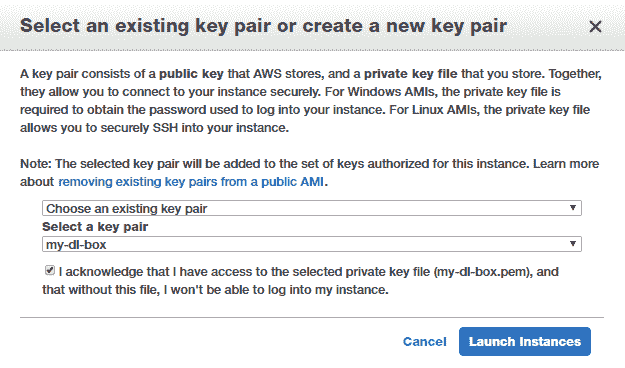 如果您沒有現有的密鑰對，則可以創建一個新的密鑰對，將私鑰文件安全地存儲到磁盤上，然后啟動實例，如以下屏幕快照所示：  請注意，虛擬服務器啟動和啟動可能需要幾分鐘，因此您可能需要稍等片刻。 通常，您可能會發現由于帳戶的限制或容量不足而導致實例啟動失敗。 如果遇到此問題，您可以請求增加使用的特定實例類型的限制（在我們的例子中為`p2.xlarge`）：  通常，AWS 會在不到 24 小時內響應并批準您的請求，因此您可能需要稍等片刻才能獲得批準，然后才可以啟動實例。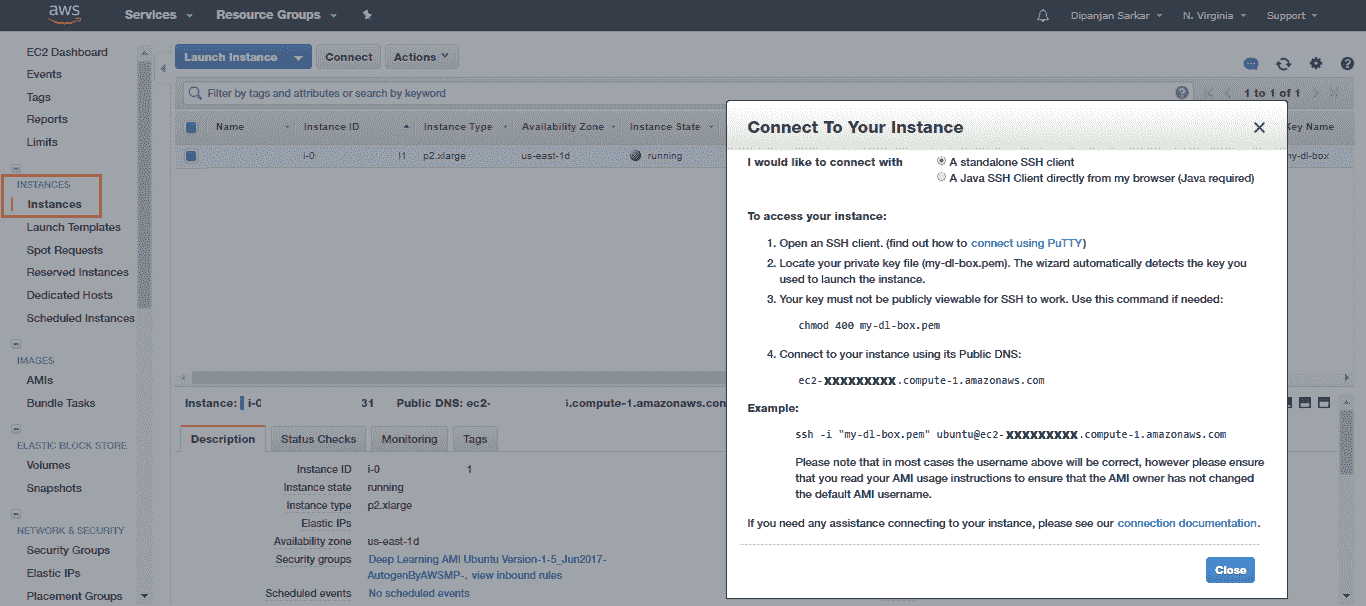 啟動實例后，您可以簽出“實例”部分并嘗試連接到該實例：  您可以使用本地系統中的命令提示符或終端（之前已存儲了先前的私有 AWS 密鑰）來立即連接到實例： ```py [DIP.DipsLaptop]> ssh -i "my-dl-box.pem" ubuntu@ec2-xxxxx.compute-1.amazonaws.com Warning: Permanently added 'ec2-xxxxx.compute-1.amazonaws.com' (RSA) to the list of known hosts. ======================================================================= Deep Learning AMI for Ubuntu ======================================================================= The README file for the AMI : /home/ubuntu/src/AMI.README.md Welcome to Ubuntu 14.04.5 LTS (GNU/Linux 3.13.0-121-generic x86_64) Last login: Sun Nov 26 09:46:05 2017 from 10x.xx.xx.xxx ubuntu@ip-xxx-xx-xx-xxx:~$ ``` 因此，這使您能夠成功登錄到自己的基于云的深度學習服務器！ # 配置您的虛擬服務器 讓我們設置一些基本配置，以利用 Jupyter 筆記本的功能在虛擬服務器上進行分析和深度學習建模，而無需始終在終端上進行編碼。 首先，我們需要設置 SSL 證書。 讓我們創建一個新目錄： ```py ubuntu@ip:~$ mkdir ssl ubuntu@ip:~$ cd ssl ubuntu@ip:~/ssl$ ``` 進入目錄后，我們將利用 OpenSSL 創建新的 SSL 證書： ```py ubuntu@ip:~/ssl$ sudo openssl req -x509 -nodes -days 365 -newkey rsa:1024 -keyout "cert.key" -out "cert.pem" -batch Generating a 1024 bit RSA private key ......++++++ ...++++++ writing new private key to 'cert.key' ----- ubuntu@ip:~/ssl2$ ls cert.key cert.pem ``` 現在，我們需要在前面提到的 Jupyter 筆記本中添加基于密碼的安全性的附加層。 為此，我們需要修改 Jupyter 的默認配置設置。 如果您沒有 Jupyter 的`config`文件，則可以使用以下命令生成它： ```py $ jupyter notebook --generate-config ``` 要為筆記本計算機啟用基于密碼的安全性，我們需要首先生成一個密碼及其哈希。 我們可以如下利用`Ipython.lib`中的`passwd()`函數： ```py ubuntu@ip:~$ ipython Python 3.4.3 (default, Nov 17 2016, 01:08:31) Type 'copyright', 'credits' or 'license' for more information IPython 6.1.0 -- An enhanced Interactive Python. Type '?' for help. In [1]: from IPython.lib import passwd In [2]: passwd() Enter password: Verify password: Out[2]: 'sha1:e9ed12b73a30:142dff0cdcaf375e4380999a6ca17b47ce187eb6' In [3]: exit ubuntu@:~$ ``` 輸入密碼并進行驗證后，該函數將向您返回一個哈希值，即您的密碼哈希值（在這種情況下，我鍵入的密碼密鑰實際上是單詞`password`，因此您絕對不應使用！）。 復制并保存該哈希值，因為我們很快將需要它。 接下來，啟動您喜歡的文本編輯器以編輯 Jupyter `config`文件，如下所示： ```py ubuntu@ip:~$ vim ~/.jupyter/jupyter_notebook_config.py # Configuration file for jupyter-notebook. c = get_config() # this is the config object c.NotebookApp.certfile = u'/home/ubuntu/ssl/cert.pem' c.NotebookApp.keyfile = u'/home/ubuntu/ssl/cert.key' c.IPKernelApp.pylab = 'inline' c.NotebookApp.ip = '*' c.NotebookApp.open_browser = False c.NotebookApp.password = 'sha1:e9ed12b73a30:142dff0cdcaf375e4380999a6ca17b47ce187eb6' # replace this # press i to insert new text and then press 'esc' and :wq to save and exit ubuntu@ip:~$ ``` 現在，在開始構建模型之前，我們將研究實現深度學習的一些基本依賴項。 # 安裝和更新深度學習依賴項 深度學習有幾個主要方面，并且針對 Python 利用 GPU 支持的深度學習。 我們將盡力介紹基本知識，但可以根據需要隨時參考其他在線文檔和資源。 您也可以跳過這些步驟，轉到下一部分，以測試服務器上是否已啟用啟用 GPU 的深度學習。 較新的 AWS 深度學習 AMI 設置了支持 GPU 的深度學習。 但是，通常設置不是最好的，或者某些配置可能是錯誤的，因此（如果您看到深度學習沒有利用您的 GPU，（從下一部分的測試中），您可能需要遍歷這些知識。 您可以轉到“訪問深度學習云環境”和“驗證深度學習環境上的 GPU 啟用”部分，以檢查 Amazon 提供的默認設置是否有效。 然后，您無需麻煩執行其余步驟！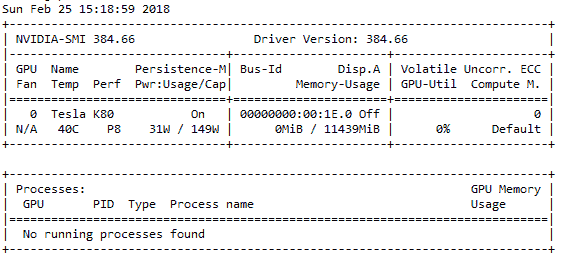 首先，您需要檢查是否已啟用 Nvidia GPU，以及 GPU 的驅動程序是否已正確安裝。 您可以利用以下命令進行檢查。 請記住，p2.x 通常配備有 Tesla GPU： ```py ubuntu@ip:~$ sudo lshw -businfo | grep -i display pci@0000:00:02.0 display GD 5446 pci@0000:00:1e.0 display GK210GL [Tesla K80] ubuntu@ip-172-31-90-228:~$ nvidia-smi ``` 如果正確安裝了驅動程序，則應該看到類似于以下快照的輸出：  如果出現錯誤，請按照以下步驟安裝 Nvidia GPU 驅動程序。 切記根據您使用的 OS 使用其他驅動程序鏈接。 我有一個較舊的 Ubuntu 14.04 AMI，為此，我使用了以下命令： ```py # check your OS release using the following command ubuntu@ip:~$ lsb_release -a No LSB modules are available. Distributor ID: Ubuntu Description: Ubuntu 14.04.5 LTS Release: 14.04 Codename: trusty # download and install drivers based on your OS ubuntu@ip:~$ http://developer.download.nvidia.com/compute/cuda/repos/ubuntu1404/ x86_64/cuda-repo-ubuntu1404_8.0.61-1_amd64.deb ubuntu@ip:~$ sudo dpkg -i ./cuda-repo-ubuntu1404_8.0.61-1_amd64.deb ubuntu@ip:~$ sudo apt-get update ubuntu@ip:~$ sudo apt-get install cuda -y # Might need to restart your server once # Then check if GPU drivers are working using the following command ubuntu@ip:~$ nvidia-smi ``` 如果您能夠根據之前的命令查看驅動程序和 GPU 硬件詳細信息，則說明驅動程序已成功安裝！ 現在，您可以集中精力安裝 Nvidia CUDA 工具包。 通常，CUDA 工具包為我們提供了一個用于創建高表現 GPU 加速應用的開發環境。 這就是用來優化和利用我們 GPU 硬件的全部功能的工具。 您可以在[這個頁面](https://developer.nvidia.com/cuda-toolkit)上找到有關 CUDA 的更多信息并下載工具包。 請記住，CUDA 非常特定于版本，并且我們的 Python 深度學習框架的不同版本僅與特定 CUDA 版本兼容。 我將在本章中使用 CUDA 8。 如果已經為您安裝了 CUDA，并且與服務器上的深度學習生態系統一起正常工作，請跳過此步驟。 要安裝 CUDA，請運行以下命令： ```py ubuntu@ip:~$ wget https://s3.amazonaws.com/personal-waf/cuda_8.0.61_375.26_linux.run ubuntu@ip:~$ sudo rm -rf /usr/local/cuda* ubuntu@ip:~$ sudo sh cuda_8.0.61_375.26_linux.run # press and hold s to skip agreement and also make sure to select N when asked if you want to install Nvidia drivers # Do you accept the previously read EULA? # accept # Install NVIDIA Accelerated Graphics Driver for Linux-x86_64 361.62? # ************************* VERY KEY **************************** # ******************** DON"T SAY Y ****************************** # n # Install the CUDA 8.0 Toolkit? # y # Enter Toolkit Location # press enter # Do you want to install a symbolic link at /usr/local/cuda? # y # Install the CUDA 8.0 Samples? # y # Enter CUDA Samples Location # press enter # Installing the CUDA Toolkit in /usr/local/cuda-8.0 … # Installing the CUDA Samples in /home/liping … # Copying samples to /home/liping/NVIDIA_CUDA-8.0_Samples now… # Finished copying samples. ``` 一旦安裝了 CUDA，我們還需要安裝 cuDNN。 該框架也由 Nvidia 開發，代表 **CUDA 深度神經網絡**（**cuDNN**）庫。 本質上，該庫是 GPU 加速的庫，由用于深度學習和構建深度神經網絡的多個優化原語組成。 cuDNN 框架為標準深度學習操作和層（包括常規激活層，卷積和池化層，歸一化和反向傳播）提供了高度優化和優化的實現！ 該框架的目的是加快深度學習模型的訓練和表現，特別是針對 Nvidia GPU 的深度學習模型。 您可以在[這個頁面](https://developer.nvidia.com/cudnn)上找到有關 cuDNN 的更多信息。 讓我們使用以下命令安裝 cuDNN： ```py ubuntu@ip:~$ wget https://s3.amazonaws.com/personal-waf/cudnn-8.0- linux-x64-v5.1.tgz ubuntu@ip:~$ sudo tar -xzvf cudnn-8.0-linux-x64-v5.1.tgz ubuntu@ip:~$ sudo cp cuda/include/cudnn.h /usr/local/cuda/include ubuntu@ip:~$ sudo cp cuda/lib64/libcudnn* /usr/local/cuda/lib64 ubuntu@ip:~$ sudo chmod a+r /usr/local/cuda/include/cudnn.h /usr/local/cuda/lib64/libcudnn* ``` 完成后，請記住使用您喜歡的編輯器（我們使用`vim`）將以下幾行添加到`~/.bashrc`的末尾： ```py ubuntu@ip:~$ vim ~/.bashrc # add these lines right at the end and press esc and :wq to save and # quit export LD_LIBRARY_PATH="$LD_LIBRARY_PATH:/usr/local/cuda/lib64:/usr/local/cuda /extras/CUPTI/lib64" export CUDA_HOME=/usr/local/cuda export DYLD_LIBRARY_PATH="$DYLD_LIBRARY_PATH:$CUDA_HOME/lib" export PATH="$CUDA_HOME/bin:$PATH" ubuntu@ip:~$ source ~/.bashrc ``` 通常，這會處理我們 GPU 的大多數必需依賴項。 現在，我們需要安裝并設置 Python 深度學習依賴項。 通常，AWS AMI 隨 Anaconda 發行版一起安裝。 但是，如果它不存在，您可以始終參考[這里](https://www.anaconda.com/download)以根據 Python 和 OS 版本下載您選擇的發行版。 通常，我們使用 Linux / Windows 和 Python3 并利用本書中的 TensorFlow 和 Keras 深度學習框架。 在 AWS AMI 中，可能會安裝不兼容的框架版本，這些框架版本不適用于 CUDA，或者可能是純 CPU 版本。 以下命令安裝 TensorFlow 的 GPU 版本，該版本在 CUDA 8 上最有效： ```py # uninstall previously installed versions if any ubuntu@ip:~$ sudo pip3 uninstall tensorflow ubuntu@ip:~$ sudo pip3 uninstall tensorflow-gpu # install tensorflow GPU version ubuntu@ip:~$ sudo pip3 install --ignore-installed --upgrade https://storage.googleapis.com/tensorflow/linux/gpu/tensorflow_gpu-1.2.0-cp34-cp34m-linux_x86_64.whl ``` 接下來，我們需要將 Keras 升級到最新版本，并刪除所有剩余的`config`文件： ```py ubuntu@ip:~$ sudo pip install keras --upgrade ubuntu@ip:~$ sudo pip3 install keras --upgrade ubuntu@ip:~$ rm ~/.keras/keras.json ``` 現在，我們幾乎準備開始利用云上的深度學習設置。 緊緊抓住！ # 訪問您的深度學習云環境 我們真的不想一直坐在服務器上的終端并在其中進行編碼。 由于我們要利用 Jupyter 筆記本進行交互式開發，因此我們將從本地系統訪問云服務器上的筆記本。 為此，我們首先需要在遠程實例上啟動 Jupyter 筆記本服務器。 登錄到您的虛擬服務器并啟動 Jupyter 筆記本服務器： ```py [DIP.DipsLaptop]> ssh -i my-dl-box.pem ubuntu@ec2-xxxxx.compute-1.amazonaws.com =================================== Deep Learning AMI for Ubuntu =================================== Welcome to Ubuntu 14.04.5 LTS (GNU/Linux 3.13.0-121-generic x86_64) Last login: Sun Feb 25 18:23:47 2018 from 10x.xx.xx.xxx # navigate to a directory where you want to store your jupyter notebooks ubuntu@ip:~$ cd notebooks/ ubuntu@ip:~/notebooks$ jupyter notebook [I 19:50:13.372 NotebookApp] Writing notebook server cookie secret to /run/user/1000/jupyter/notebook_cookie_secret [I 19:50:13.757 NotebookApp] Serving notebooks from local directory: /home/ubuntu/notebooks [I 19:50:13.757 NotebookApp] 0 active kernels [I 19:50:13.757 NotebookApp] The Jupyter Notebook is running at: https://[all ip addresses on your system]:8888/ [I 19:50:13.757 NotebookApp] Use Control-C to stop this server and shut down all kernels (twice to skip confirmation). ``` 現在，我們需要在本地實例上啟用端口轉發，以便從本地計算機的瀏覽器訪問服務器筆記本。 利用以下語法： ```py sudo ssh -i my-dl-box.pem -N -f -L local_machine:local_port:remote_machine:remote_port ubuntu@ec2-xxxxx.compute-1.amazonaws.com ``` 這將開始將本地計算機的端口（在我的情況下為`8890`）轉發到遠程虛擬服務器的端口`8888`。 以下是我用于設置的內容： ```py [DIP.DipsLaptop]> ssh -i "my-dl-box.pem" -N -f -L localhost:8890:localhost:8888 ubuntu@ec2-52-90-91-166.compute-1.amazonaws.com ``` 這也稱為 **SSH 隧道**。 因此，一旦開始轉發，請轉到本地瀏覽器并導航到`localhost`地址`https://localhost:8890`，我們將其轉發到虛擬服務器中的遠程筆記本服務器。 確保您在地址中使用`https`，否則會收到 SSL 錯誤。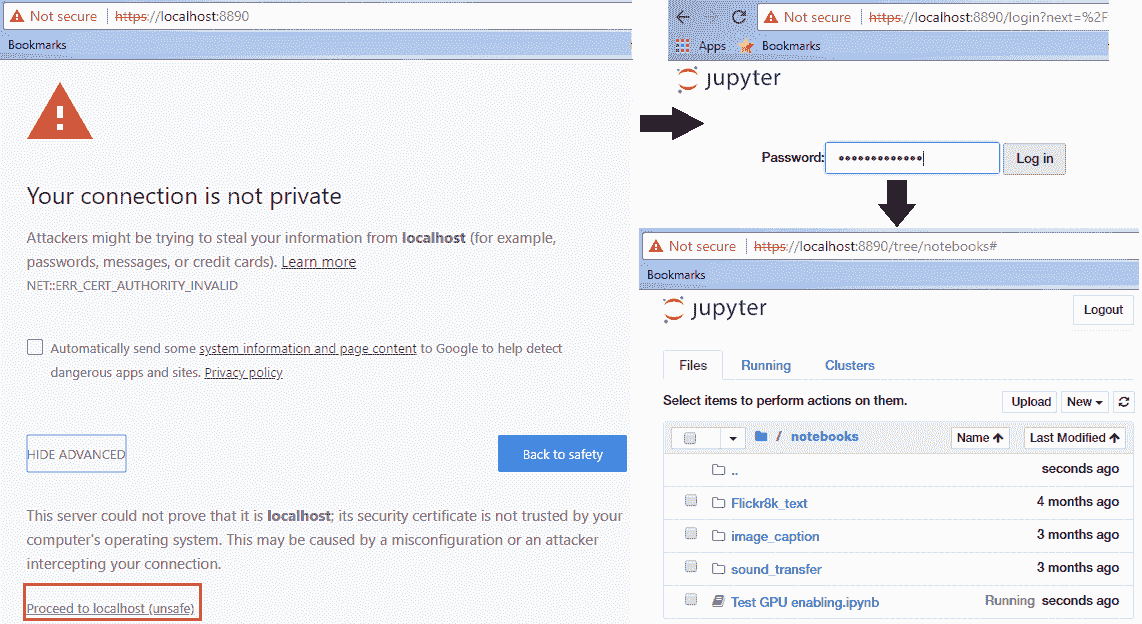 如果到目前為止您已正確完成所有操作，則應在瀏覽器中看到一個警告屏幕，并且按照以下屏幕截圖中的步驟進行操作，則在任何筆記本上工作時，都應該會看到熟悉的 Jupyter 用戶界面：  您可以放心地忽略“您的連接不是私人警告”； 之所以顯示它，是因為我們自己生成了 SSL 證書，并且尚未得到任何可信機構的驗證。 # 在您的深度學習環境中驗證 GPU 的啟用 最后一步是確保一切正常，并且我們的深度學習框架正在利用我們的 GPU（我們需要按小時支付！）。 您可以參考`Test GPU enabling.ipynb` Jupyter 筆記本來測試所有代碼。 我們將在這里詳細介紹。 我們首先要驗證的是`keras`和`tensorflow`是否已正確加載到我們的服務器中。 可以通過如下導入它們來驗證： ```py import keras import tensorflow Using TensorFlow backend. ``` 如果您看到前面的代碼加載沒有錯誤，那就太好了！ 否則，您可能需要追溯以前執行的步驟，并在線搜索要獲取的特定錯誤； 查看每個框架的 GitHub 存儲庫。 最后一步是檢查`tensorflow`是否已啟用以使用我們服務器的 Nvidia GPU。 您可以使用以下測試對此進行驗證： ```py In [1]: from tensorflow.python.client import device_lib ...: device_lib.list_local_devices() Out [1]: [name: "/cpu:0" device_type: "CPU" memory_limit: 268435456 locality { } incarnation: 9997170954542835749, name: "/gpu:0" device_type: "GPU" memory_limit: 11324823962 locality { bus_id: 1 } incarnation: 10223482989865452371 physical_device_desc: "device: 0, name: Tesla K80, pci bus id: 0000:00:1e.0"] ``` 如果您觀察到上述輸出，則可以看到我們的 GPU 列在設備列表中，因此在訓練我們的深度學習模型時它將利用相同的 GPU。 您已經在云上成功建立了強大的深度學習環境，您現在可以使用它使用 GPU 來更快地訓練深度學習模型！ 永遠記住，AWS 按小時收費實例，并且您不希望在完成分析和構建模型后保持實例運行。 您始終可以根據需要從 EC2 控制臺重新啟動實例。 # 建立具有 GPU 支持的強大的本地深度學習環境 通常，用戶或組織可能不希望利用云服務，尤其是在其數據敏感的情況下，因此要專注于構建本地深度學習環境。 這里的主要重點應該是投資于正確的硬件類型，以實現最佳表現并利用正確的 GPU 來構建深度學習模型。 關于硬件，特別強調以下方面： * **處理器**：如果您想寵愛自己，則可以投資 i5 或 i7 Intel CPU，或者 Intel Xeon。 * **RAM**：為您的內存至少投資 32 GB DDR4 或更好的 RAM。 * **磁盤**：1 TB 硬盤非常好，您還可以投資最少 128 GB 或 256 GB 的 SSD 來快速訪問數據！ * **GPU**：也許是深度學習中最重要的組件。 投資 NVIDIA GPU，以及擁有 8 GB 以上 GTX 1070 的所有產品。 您不應該忽略的其他事項包括主板，電源，堅固的外殼和散熱器。 設置完鉆機之后，對于軟件配置，您可以重復上一部分中的所有步驟，但不包括云設置，您應該一切順利！ # 神經網絡基礎 讓我們嘗試熟悉一下神經網絡背后的一些基本概念，這些基本概念使所有深度學習模型都獲得成功！ # 一個簡單的線性神經元 線性神經元是深度神經網絡的最基本組成部分。 可以如下圖所示。 在這里，`X = {x1, ... ,xn}`代表輸入向量， `w[i]`是神經元的權重。 給定一個包含一組輸入目標值對的訓練集，線性神經元嘗試學習一種線性變換，該變換可以將輸入向量映射到相應的目標值。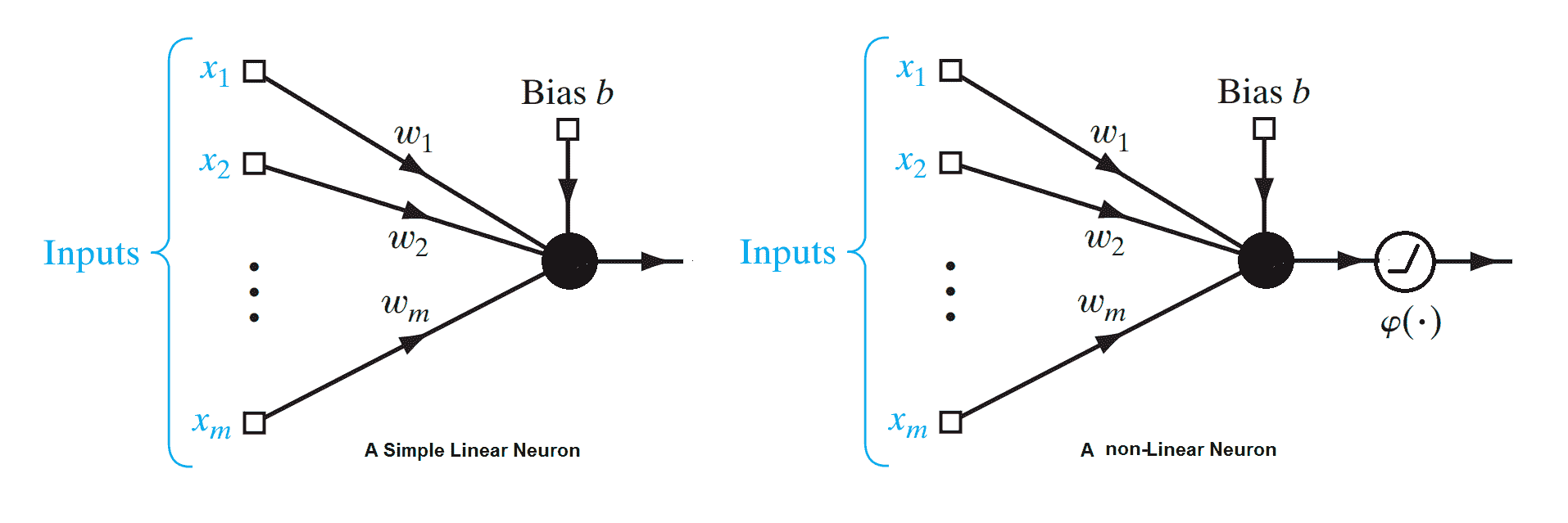 基本上，線性神經元通過線性函數`W^T x = y`近似輸入輸出關系：  簡單線性神經元和簡單非線性神經元的示意圖 讓我們嘗試用這個簡單的神經元為玩具問題建模。 員工 *A* 從自助餐廳購買午餐。 他們的飲食包括魚，薯條和番茄醬。 他們每個人得到幾個部分。 收銀員只告訴他們一頓飯的總價。 幾天后，他們能算出每份的價格嗎？ 好吧，這聽起來像一個簡單的線性編程問題，可以很容易地通過解析來解決。 讓我們使用前面的線性神經單元來表示這個問題。 在這里，`X = {x[fish], x[ketchup], x[chips]}`和我們有相應的權重`(w[fish], w[ketchup], w[chips])`。 每個進餐價格對各部分的價格給出線性約束：  假設`t[n]`為真實價格，`y[n]`由我們的模型估計的價格，由前面的線性方程式給出。 目標與我們的估計之間的剩余價格差為`t[n] - y[n]`。 現在，不同餐點的這些殘差可以為正或負，并且可以抵消，從而使總體誤差為零。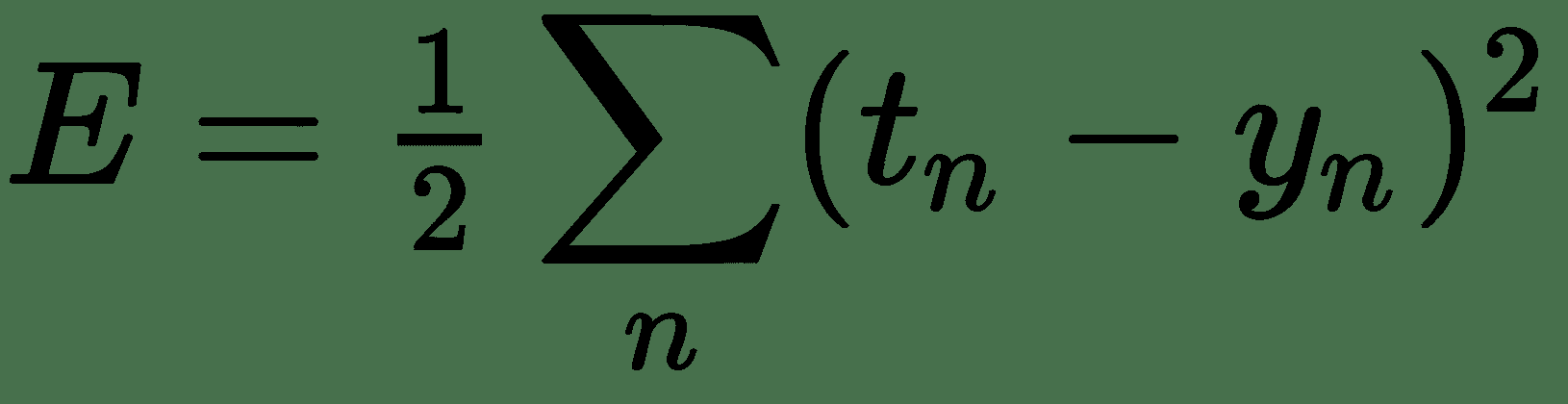 處理此問題的一種方法是使用平方和殘差：  如果我們能夠最大程度地減少此誤差，則可以對每件商品的一組權重/價格進行很好的估計。 因此，我們得出了一個優化問題。 讓我們首先討論一些解決優化問題的方法。 # 基于梯度的優化 優化基本上涉及最小化或最大化某些函數`f(x)`，其中`x`是數值向量或標量。 在此，`f(x)`被稱為**目標函數**或**準則**。 在神經網絡中，我們稱其為成本函數，損失函數或誤差函數。 在前面的示例中，我們要最小化的損失函數為`E`。 假設我們有一個函數`y = f(x)`，其中`x`和`y`是實數。 此函數的導數告訴我們此函數如何隨`x`的微小變化而變化。 因此，可以通過無窮大地更改`x`來使用導數來減小函數的值。 假設對于`x`，`f'(x) > 0`。 這意味著，如果我們沿著`x`的正數增加`x`，則`f(x)`將會增加，因此對于足夠小的`ε`，`f(x-ε) < f(x)`。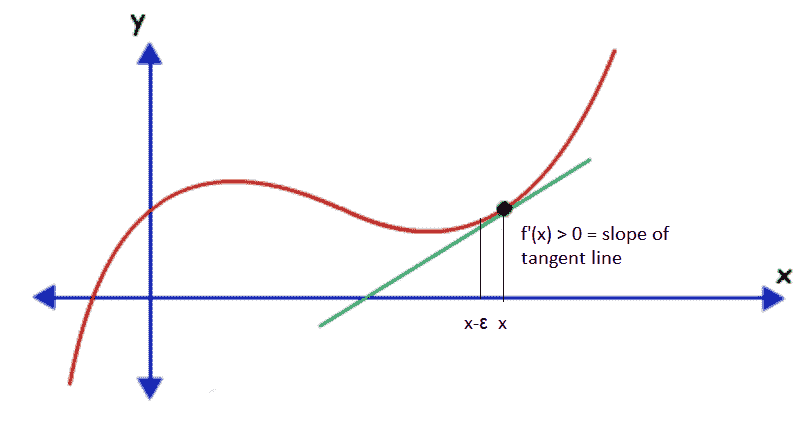 注意`f(x)`可以通過在導數的相反方向以小步長移動`x`來減少：  函數值沿導數的相反方向或相反方向的變化方式 如果導數`f'(x) < 0`，則導數不提供信息，我們需要朝哪個方向移動以達到函數最小值。 在局部最優（最小/最大）時，導數可以為零。 如果`x`處的函數`f(x)`的值小于所有相鄰點，則將點稱為**局部最小值**。 同樣，我們可以定義一個局部最大值。 某些點既不能是最大值，也不能是最小值，但是導數`f'(x)`在這些點上為零。 這些稱為**鞍**點。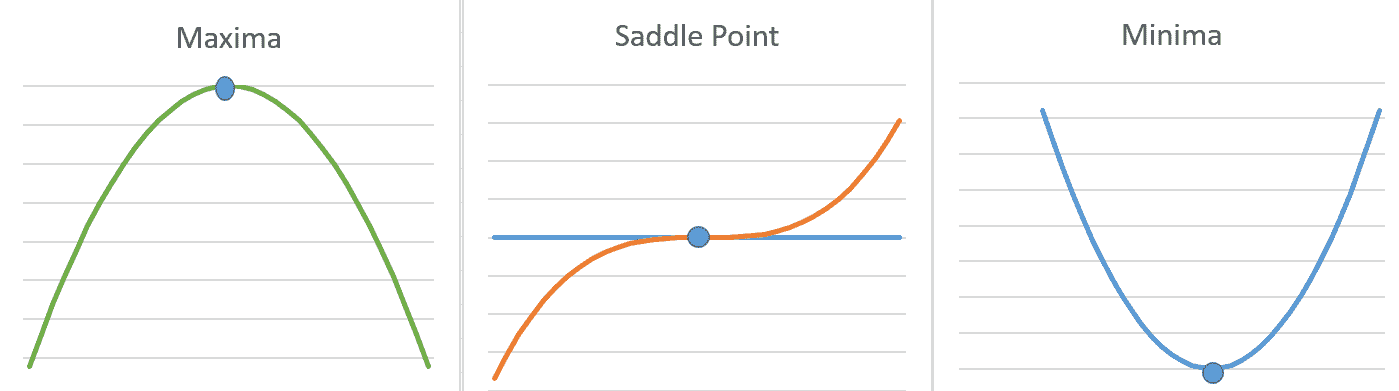 下圖說明了`f'(x) = 0`的三種情況：  單個變量函數的最小，最大和鞍點。 在所有三個突出顯示的點上導數`f'(x) = 0` 在`x`的所有可能值中達到`f`的最小值的點稱為**全局最小值**。 一個函數可以具有一個或多個全局最小值。 可能存在局部最小值，而不是全局最小值。 但是，如果函數是凸函數，則可以保證它只有一個全局最小值，而沒有局部最小值。 通常，在 ML 中，我們希望最小化幾個變量`f`的實值函數：`R^n -> R`。 幾個變量的實值函數的一個簡單示例是熱板溫度函數`f(x1, x2) = 50 - x1^2 - 2x2^2`，其在板上的坐標為`x = (x1, x2)`。 在深度學習中，我們通常最小化損失函數，該函數是多個變量（例如神經網絡中的權重）的函數。 這些函數具有許多局部最小值，許多鞍點被非常平坦的區域包圍，并且它們可能具有也可能沒有任何全局最小值。 所有這些使得優化此類函數非常困難。 幾個變量的函數的導數表示為偏導數，當我們更改其中一個輸入變量`x[i]`，并保持其他不變時，它將衡量函數的變化率。 關于所有變量的偏導數向量稱為`f`的**梯度向量**，用`?f`表示。 我們還可以找出函數相對于任意方向`v`（單位向量）的變化速度。 這是通過在單位向量`v`，即點積`?f · v`的方向上投影梯度向量`?f`來計算的。 這在`v`方向上被稱為`f`的**定向導數**，通常用`?[v]`表示。 為了使`f`最小化，我們需要找到一個方向`u`，在其中要更改`x`，以使`f`的值最大程度地減小。 令`x[a]`為非常接近`x`的點，即`||x - x[a]||`非常小。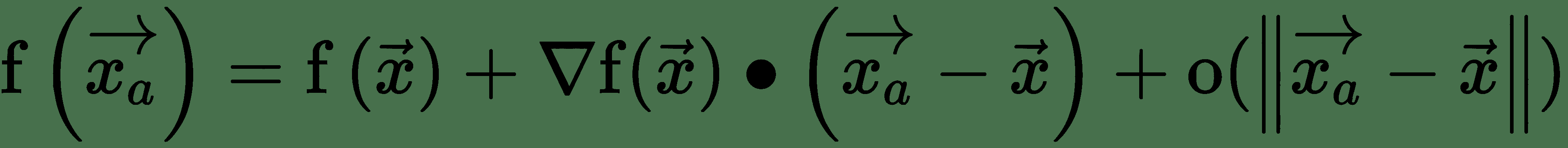 首先，泰勒級數圍繞`x`的階展開式為：  上式中的最后一項對于`x[a]`足夠接近`x`可以忽略。 第二項表示`f`沿`x[a] - x`的方向導數。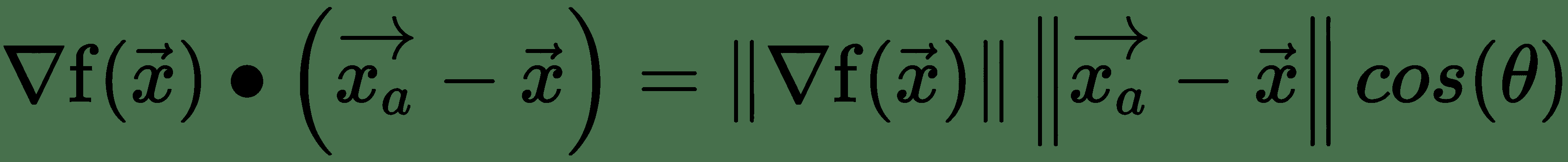 這里有：  因此，如果`cos(θ)`最小，則`f(x)`最大減小，即 -1，如果`θ = π`，即`x[a] - x`應該指向與梯度向量，`f`相反的方向，則`f(x)`會最大程度地減小。 這是最陡下降方向：`-?f`或**最陡梯度下降**的方向。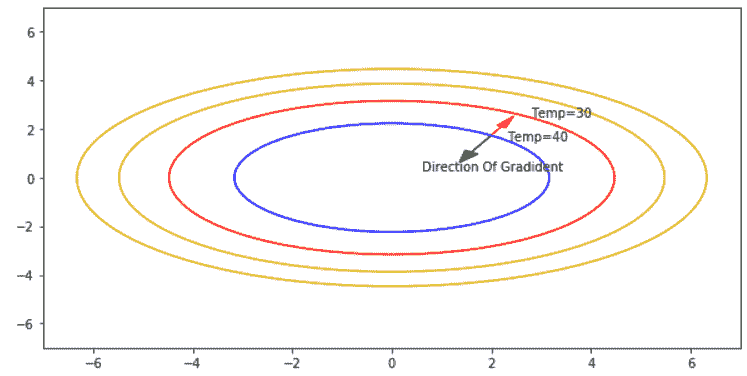 我們在下圖中對此進行說明：  熱板 *熱板*示例：給定坐標（`x`和`y`）上的溫度由函數`f(x, y) = 50 - y^2 - 2x^2`表示。 板在中心`(0, 0)`處最熱，溫度為 50。點`(x, y)`處的梯度向量由給出`f = (-4x, -2y)`。 板上的點`(2.3, 2)`的溫度為 **40**。 該點位于恒溫輪廓上。 顯然，如紅色箭頭所示，在與梯度相反的方向上移動，步長為`ε`，溫度降低至 **30**。 讓我們使用`tensorflow`實現熱板溫度函數的梯度下降優化。 我們需要初始化梯度下降，所以讓我們從`x = y = 2`開始： ```py import tensorflow as tf #Initialize Gradient Descent at x,y =(2, 2) x = tf.Variable(2, name='x', dtype=tf.float32) y = tf.Variable(2, name='y', dtype=tf.float32) temperature = 50 - tf.square(y) - 2*tf.square(x) #Initialize Gradient Descent Optimizer optimizer = tf.train.GradientDescentOptimizer(0.1) #0.1 is the learning rate train = optimizer.minimize(temperature) grad = tf.gradients(temperature, [x,y]) #Lets calculate the gradient vector init = tf.global_variables_initializer() with tf.Session() as session: session.run(init) print("Starting at coordinate x={}, y={} and temperature there is {}".format( session.run(x),session.run(y),session.run(temperature))) grad_norms = [] for step in range(10): session.run(train) g = session.run(grad) print("step ({}) x={},y={}, T={}, Gradient={}".format(step, session.run(x), session.run(y), session.run(temperature), g)) grad_norms.append(np.linalg.norm(g)) plt.plot(grad_norms) ``` 以下是前面代碼的輸出。 在每個步驟中，如梯度向量所建議的，計算`x`，`y`的新值，以使總溫度最大程度地降低。 請注意，計算出的梯度與前面所述的公式完全匹配。 我們還在每個步驟之后計算梯度范數。 以下是梯度在 10 次迭代中的變化方式： ```py Starting at coordinate x=2.0, y=2.0 and temperature there is 38.0 step (0) x=2.79,y=2.40000, T=28.55, Gradient=[-11.2, -4.8000002] step (1) x=3.92,y=2.88000, T=10.97, Gradient=[-15.68, -5.7600002] .......... step (9) x=57.85,y=12.38347, T=-6796.81, Gradient=[-231.40375, -24.766947] ``` # Jacobian 矩陣和 Hessian 矩陣 有時，我們需要優化其輸入和輸出為向量的函數。 因此，對于輸出向量的每個分量，我們需要計算梯度向量。 對于`f: R^n -> R^m`，我們將有`m`個梯度向量。 通過將它們排列成矩陣形式，我們得到`n x m`個偏導數`J[ij] = ?f(x)[i]/?x[j]`的矩陣，稱為 **Jacobian 矩陣**。 對于單個變量的實值函數，如果要在某個點測量函數曲線的曲率，則需要計算在更改輸入時導數將如何變化。 這稱為**二階導數**。 二階導數為零的函數沒有曲率，并且是一條平線。 現在，對于幾個變量的函數，有許多二階導數。 這些導數可以布置在稱為 **Hessian 矩陣**的矩陣中。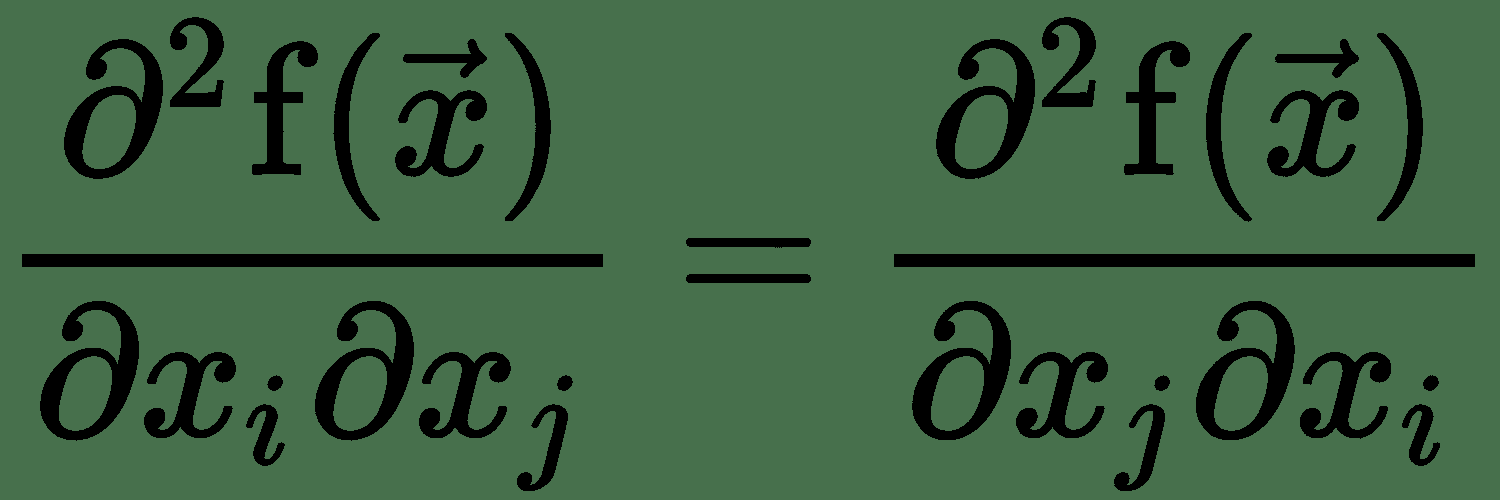 由于二階偏導數是對稱的，即：  Hessian 矩陣是實對稱的，因此具有實特征值。 相應的特征向量代表不同的曲率方向。 最大和最小特征值的大小之比稱為黑森州的**條件數**。 它測量沿每個本征維的曲率彼此相差多少。 當 Hessian 條件數較差時，梯度下降的效果較差。 這是因為，在一個方向上，導數迅速增加，而在另一個方向上，它緩慢地增加。 梯度下降并沒有意識到這一變化，因此，可能需要很長時間才能收斂。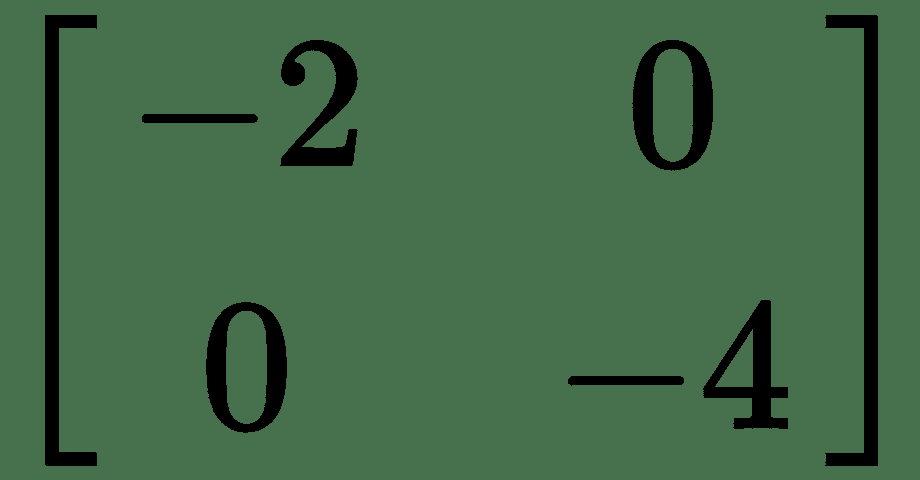 對于我們的溫度示例，Hessian 為：  最大曲率的方向是最小曲率的方向的兩倍。 因此，沿著`y`遍歷，我們將更快地到達最小點。 從前面的*熱板*圖中所示的溫度輪廓中也可以看出這一點。 我們可以使用二階導數曲率信息來檢查最佳點是最小還是最大。 對于單個變量，`f'(x) = 0`，`f''(x) > 0`表示`x`是`f`的局部最小值， 并且`f'(x) = 0`，`f''(x) < 0`表示`x`是局部最大值。 這稱為**二階導數測試**（請參見下圖*解釋曲率*）。 類似地，對于幾個變量的函數，如果 Hessian 在`x`為正定（即所有本征值均為正），則`f`會在`x`達到局部最小值。 如果 Hessian 在`x`處為負定值，則`f`在`x`處達到局部最大值。 如果 Hessian 同時具有正和負特征值，則`x`是`f`的鞍點。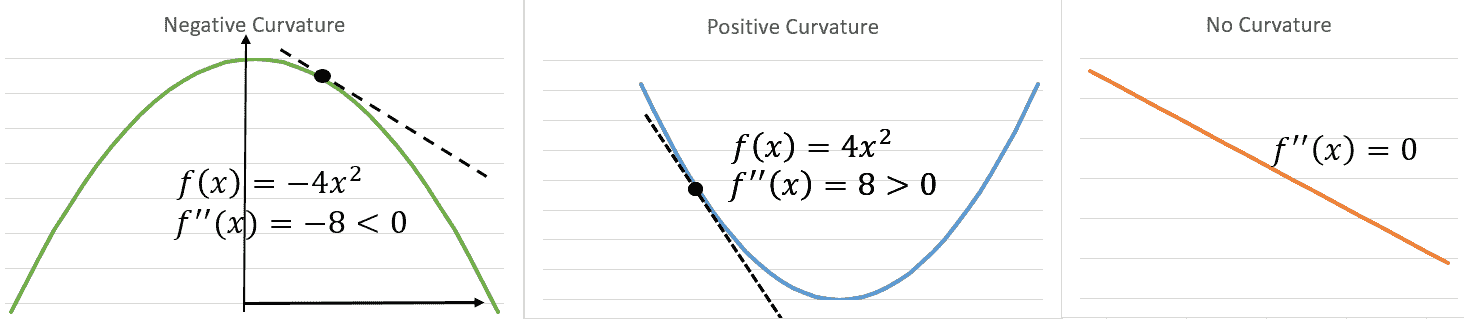 否則，測試沒有定論：  解釋曲率 存在基于使用曲率信息的二階導數的優化算法。 牛頓法就是這樣一種方法，對于凸函數，它只需一步就可以達到最佳點。 # 導數鏈式規則 令`f`和`g`均為單個變量的實值函數。 假設`y = g(x)`和`z = f(g(x)) = f(y)`。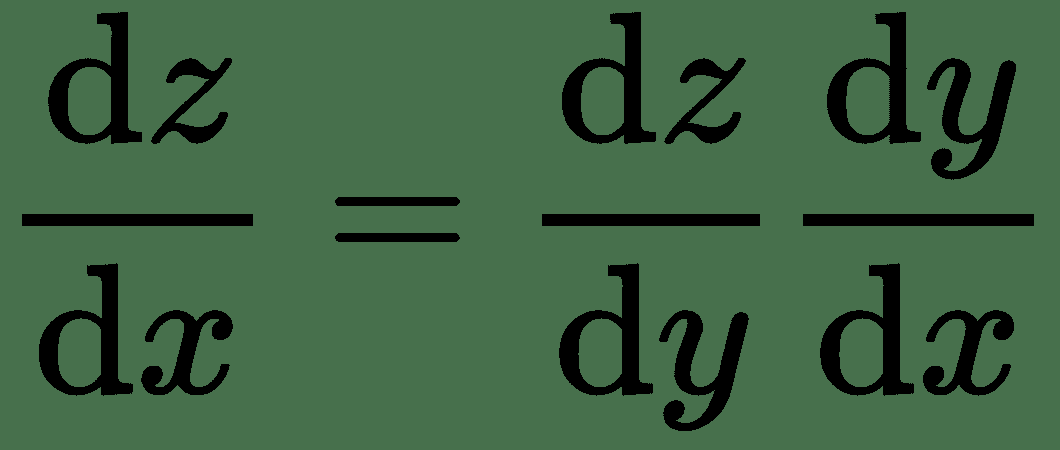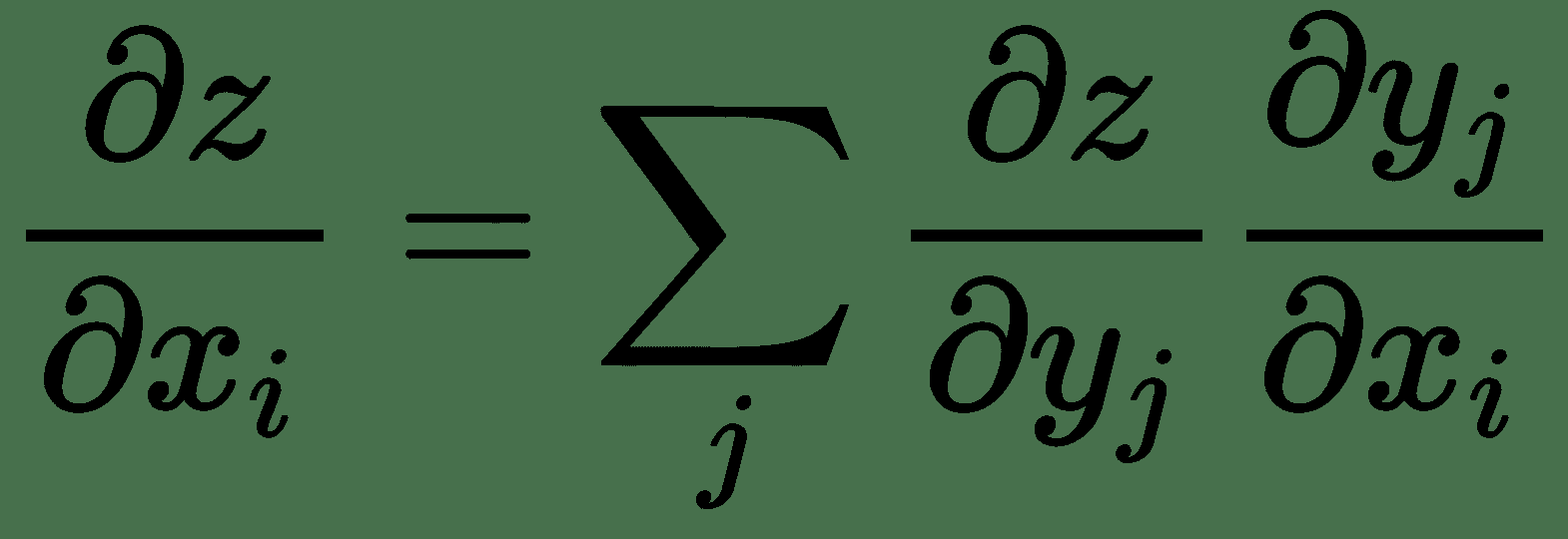 然后，導數的鏈式規則指出：  同樣，對于幾個變量的函數，令`x ∈ R^m`，`y ∈ R^n`，`g: R^m -> R^n`，`f: R^n -> R`，`y = g(x)`，`z = f(y)`，然后：  因此，`z`相對于`x`的梯度`?z/?x`表示為 Jacobian `?y/?x`與`?z/?y`梯度向量的乘積。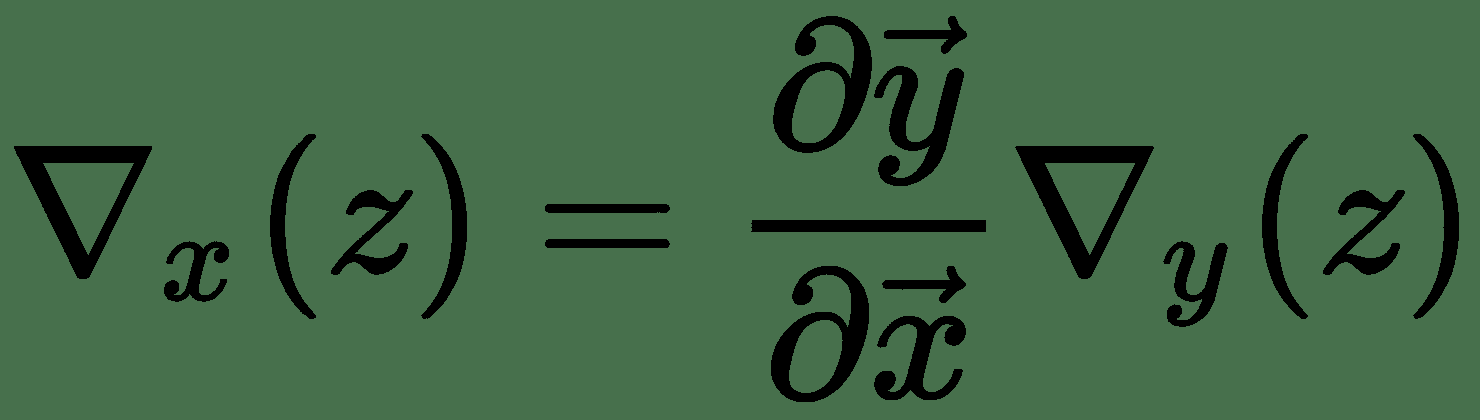 因此，對于多個變量的函數，我們具有導數的鏈式規則，如下所示：  神經網絡學習算法由幾個這樣的雅可比梯度乘法組成。 # 隨機梯度下降 幾乎所有的神經網絡學習都由一種非常重要的算法提供支持：SGD。 這是常規梯度下降算法的擴展。 在 ML 中，損失函數通常寫為樣本損失函數之和，作為*自助餐廳示例*中的平方誤差`E`。 因此，如果我們有`m`個訓練示例，則梯度函數也將具有`m`個可加項。 梯度的計算成本隨著`m`線性增加。 對于十億大小的訓練集，前面的梯度計算將花費很長時間，并且梯度下降算法將朝著收斂的方向非常緩慢地進行，從而在實踐中無法進行學習。 SGD 取決于對梯度實際上是期望值的簡單理解。 我們可以通過在小樣本集上計算期望值來近似。 可以從訓練集中隨機抽取`m'`（比`m`小得多的**小批量**）樣本大小，并且梯度可以近似為計算單個梯度下降步驟。 讓我們再次考慮*自助餐廳示例*。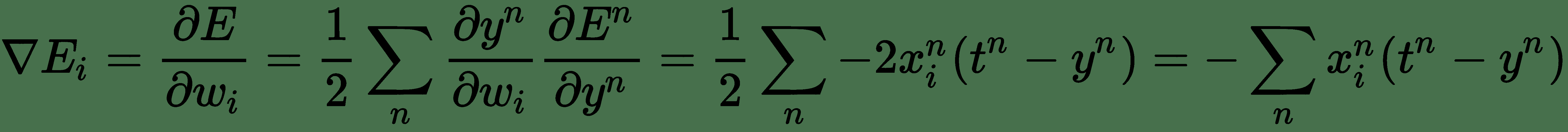 應用鏈式規則，誤差函數（三個變量的函數）的梯度由下式給出：  現在，代替使用所有 *n* 訓練示例來計算導數，如果我們從訓練示例中抽取少量隨機樣本，我們仍然可以合理地近似導數。 `E`的梯度給出了權重更新的估計值。 我們可以通過將其乘以一個常數`ε`（稱為**學習率**）來進一步控制它。 取得非常高的學習率可能會增加而不是使優化目標函數值最小化。 在 SGD 中，在將每個小批量展示給算法后，將更新權重。 將整個訓練數據一次呈現給訓練算法需要很多數據點/批量大小的步驟。 一個周期描述了算法看到*整個*數據集的次數。 以下是自助餐廳問題的`keras`代碼。 假設魚類的實際價格為 150 美分，薯條為 50 美分，番茄醬為 100 美分。 我們已隨機生成餐中物品的樣本部分。 假設初始的價格為每份 50 美分。 30 個周期后，我們得到的估計值與商品的真實價格非常接近： ```py #The true prices used by the cashier p_fish = 150; p_chips = 50; p_ketchup = 100 #sample meal prices: generate data meal prices for 10 days. np.random.seed(100) portions = np.random.randint(low=1, high=10, size=3 ) X = []; y = []; days = 10 for i in range(days): portions = np.random.randint(low=1, high=10, size=3 ) price = p_fish * portions[0] + p_chips * portions[1] + p_ketchup * portions[2] X.append(portions) y.append(price) X = np.array(X) y = np.array(y) #Create a linear model from keras.layers import Input, Dense from keras.models import Model from keras.optimizers import SGD price_guess = [np.array([[ 50 ], [ 50],[ 50 ]]) ] #initial guess of the price model_input = Input(shape=(3,), dtype='float32') model_output = Dense(1, activation='linear', use_bias=False, name='LinearNeuron', weights=price_guess)(model_input) sgd = SGD(lr=0.01) model = Model(model_input, model_output) #define the squared error loss E stochastic gradient descent (SGD) optimizer model.compile(loss="mean_squared_error", optimizer=sgd) model.summary() _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= input_4 (InputLayer) (None, 3) 0 _________________________________________________________________ LinearNeuron (Dense) (None, 1) 3 ================================================================= Total params: 3 Trainable params: 3 Non-trainable params: 0 _________________________________________________________________ #train model by iterative optimization: SGD with mini-batch of size 5. 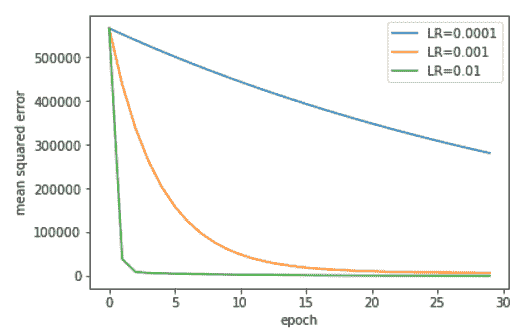history = model.fit(X, y, batch_size=5, epochs=30,verbose=2) ``` 在下圖中，我們顯示了學習率對迭代 SGD 算法收斂的影響：  學習率對自助餐廳問題 SGD 收斂速度的影響 下表顯示了 SGD 在`LR = 0.01`的連續周期如何更新價格猜測： | **周期** | **`w_fish`** | **`w_chips`** | **`w_ketchup`** | | --- | --- | --- | --- | | 0（初始） | 50 | 50 | 50 | | 1 | 124.5 | 96.3 | 127.4 | | 5 | 120.6 | 81.7 | 107.48 | | 10 | 128.4 | 74.7 | 104.6 | | 15 | 133.8 | 68.9 | 103.18 | | 30 | 143.07 | 58.2 | 101.3 | | 50 | 148.1 | 52.6 | 100.4 | # 非線性神經元 線性神經元很簡單，但是在計算上受到限制。 即使我們使用多層線性單元的深層棧，我們仍然具有僅學習線性變換的線性網絡。 為了設計可以學習更豐富的轉換集（非線性）的網絡，我們需要一種在神經網絡的設計中引入非線性的方法。 通過使輸入的線性加權總和通過非線性函數，我們可以在神經單元中引起非線性。 盡管非線性函數是固定的，但是它可以通過線性單元的權重來適應數據，權重是該函數的參數。 此非線性函數稱為非線性神經元的**激活函數**。 一個簡單的激活函數示例是二元閾值激活，相應的非線性單元稱為 **McCulloch-Pitts 單元**。 這是一個階躍函數，不可微分為零。 同樣，在非零點，其導數為零。 其他常用的激活函數是 Sigmoid，tanh 和 ReLu。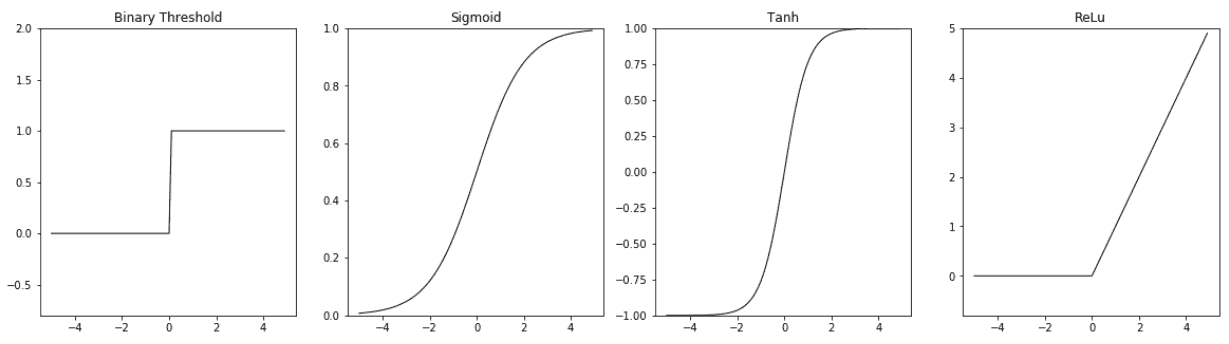 下圖提供了這些函數的定義和圖解：  激活函數圖 這是激活函數定義： | **函數名稱** | **定義** | | --- | --- | | 二元閾值 | 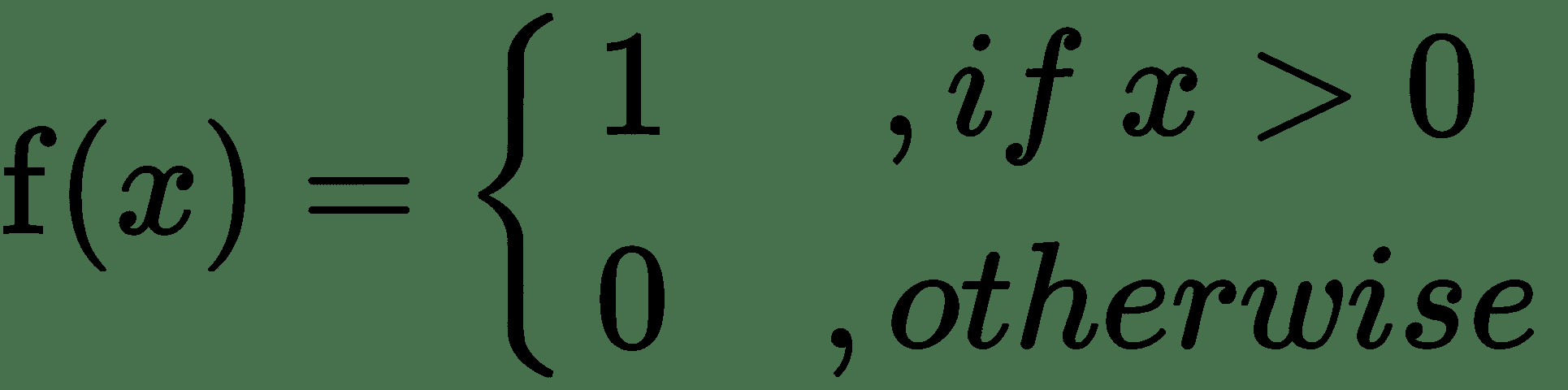 | | Sigmoid | 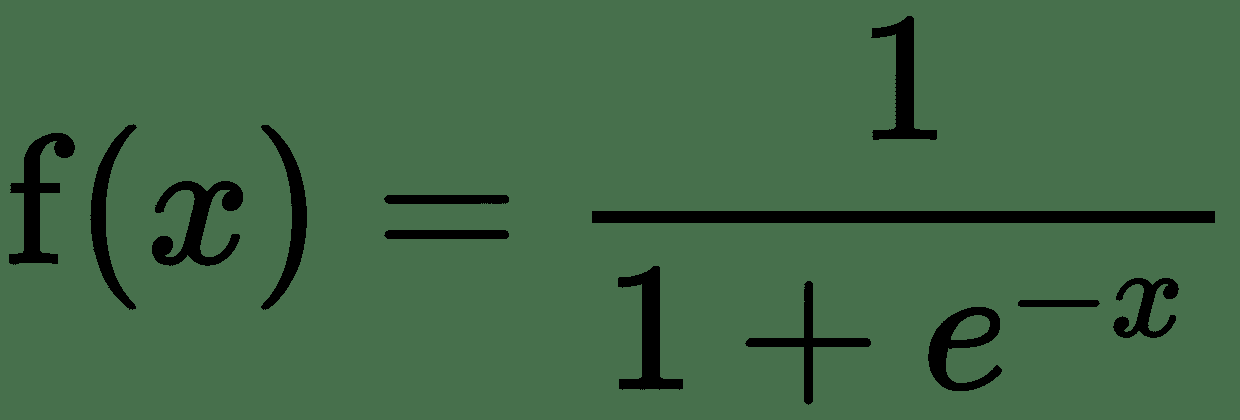 | | tanh | 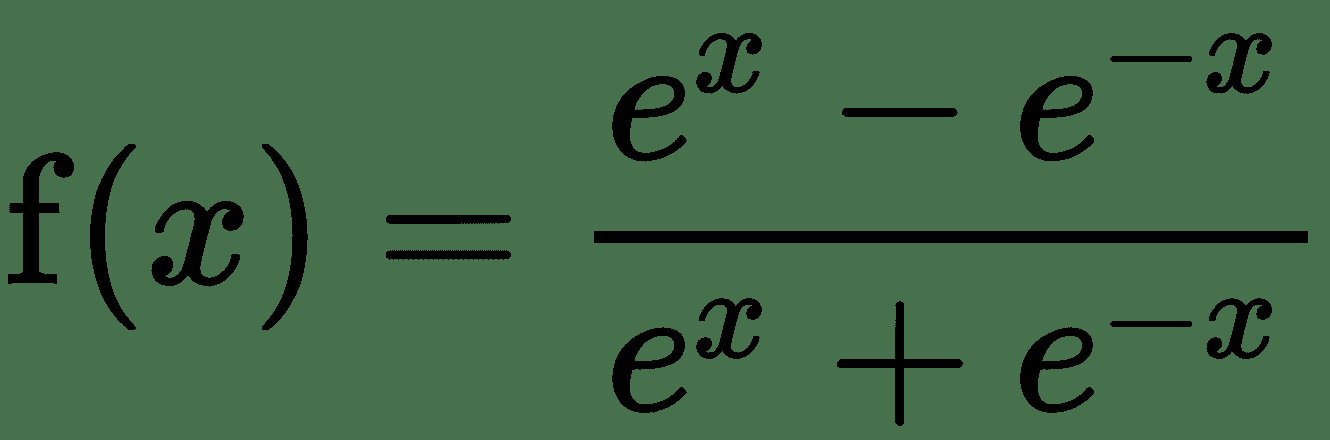 | | ReLU | 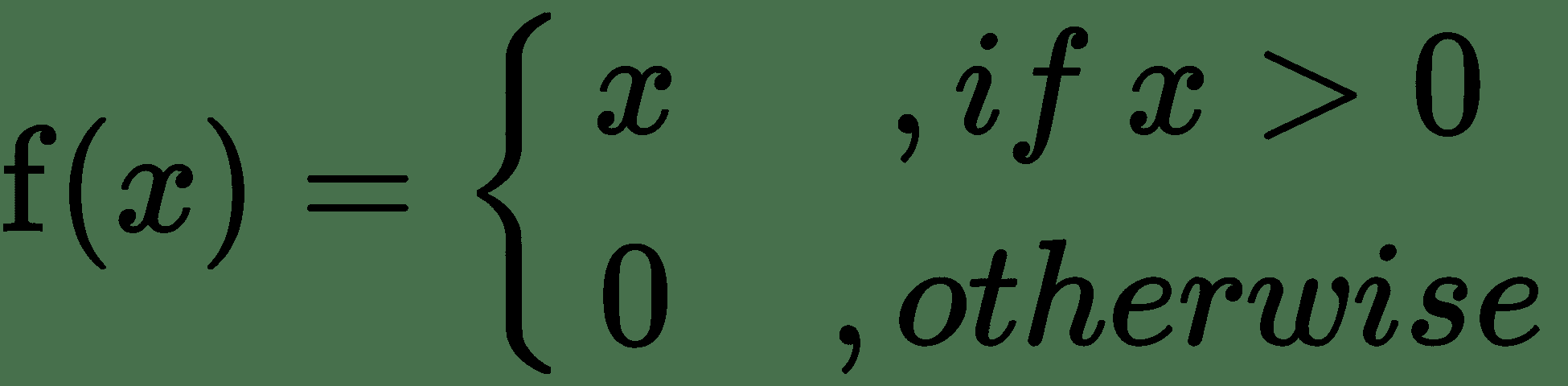 | | | 或 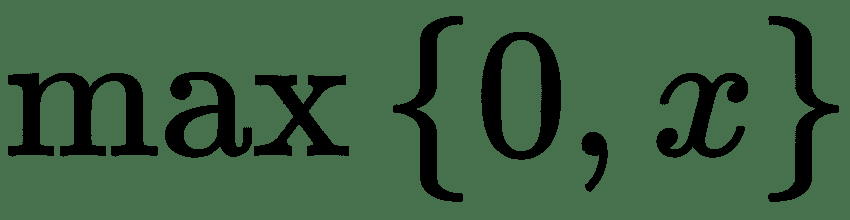 | 如果我們有一個 K 類（`K > 2`）分類問題，那么我們基本上想學習條件概率分布`P(y | x)`。 因此，輸出層應具有 K 個神經元，其值應為 1。為了使網絡了解所有 K 單元的輸出應為 1， 使用 **softmax 激活**函數。 這是 Sigmoid 激活的概括。 像 Sigmoid 函數一樣，softmax 函數將每個單元的輸出壓縮為 0 到 1 之間。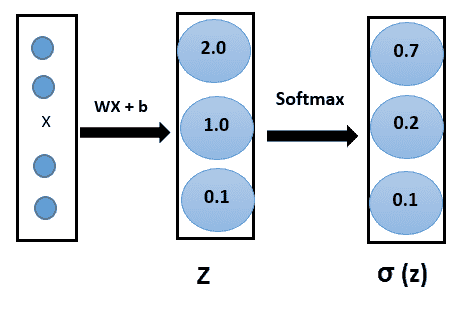 而且，它會將每個輸出相除，以使輸出的總和等于 1：  數學上，softmax 函數如下所示，其中`z`是輸出層輸入的向量（如果有 10 個輸出單元，則`z`中有 10 個元素）。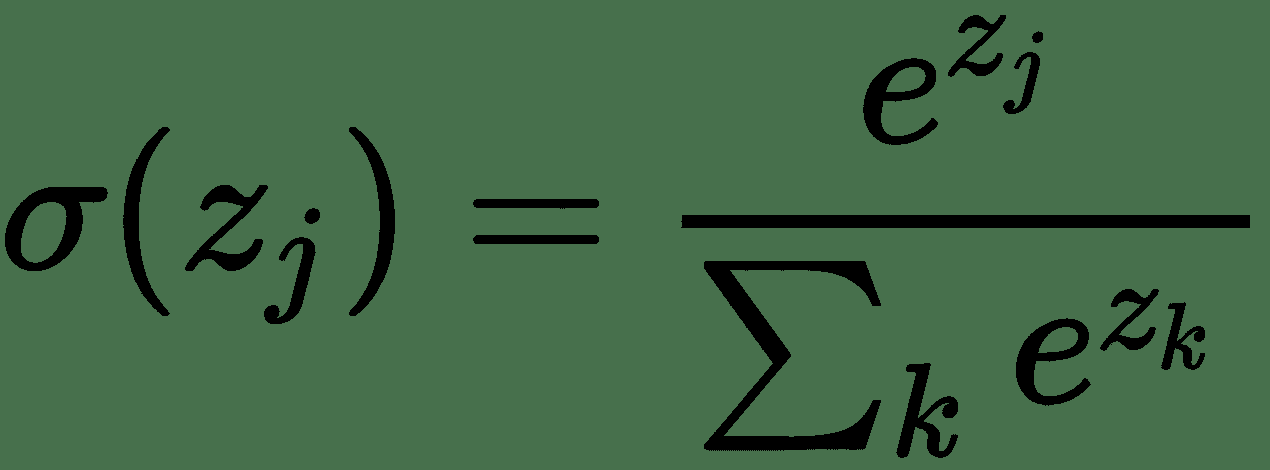 同樣，`j`索引輸出單元，因此`j = 1, 2, ..., K`：  # 學習一個簡單的非線性單元 – Logistic 單元 假設我們有兩個類分類問題； 也就是說，我們需要預測二元結果變量`y`的值。 就概率而言，結果`y`取決于特征`x`的伯努利分布。 神經網絡需要預測概率`P(y = 1 | x)`。 為了使神經網絡的輸出成為有效概率，它應該位于`[0, 1]`中。 為此，我們使用 Sigmoid 激活函數并獲得非線性邏輯單元。 要學習邏輯單元的權重，首先我們需要一個成本函數并找到成本函數的導數。 從概率的角度來看，如果我們想最大化輸入數據的可能性，則交叉熵損失會作為自然成本函數出現。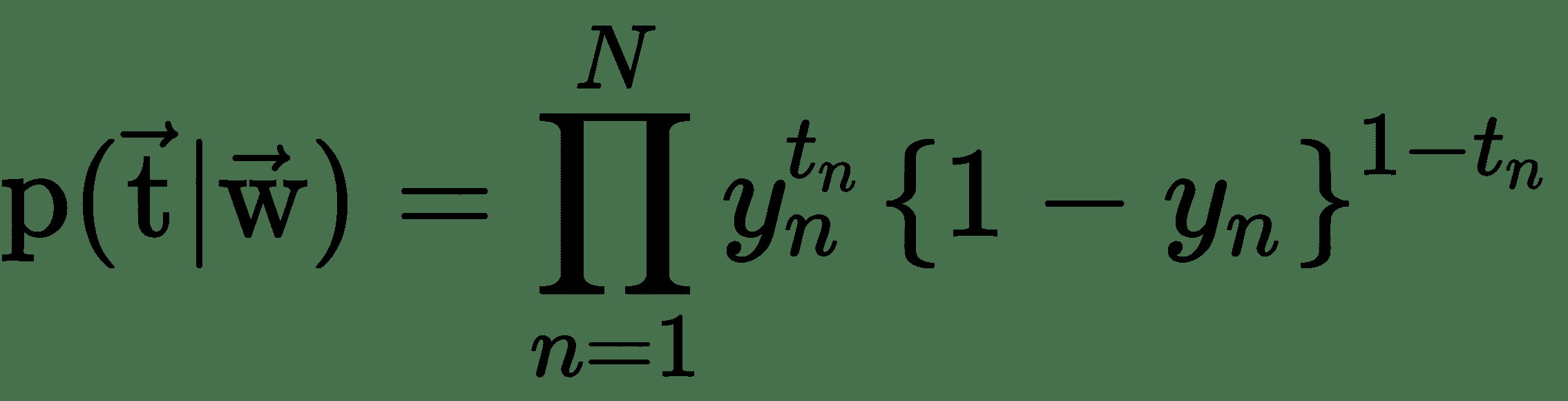 假設我們有一個訓練數據集`X = {x[n], t[n]}`，`n = 1, …, N`，似然函數可以寫成：  其中`y[n]`是在將`x[n]`作為輸入數據傳遞到邏輯單元之后，Sigmoid 單元的輸出。 注意`t`和`w`分別表示 Sigmoid 單元的目標向量（訓練集中的所有`N`個目標值）和權重向量（所有權重的集合）。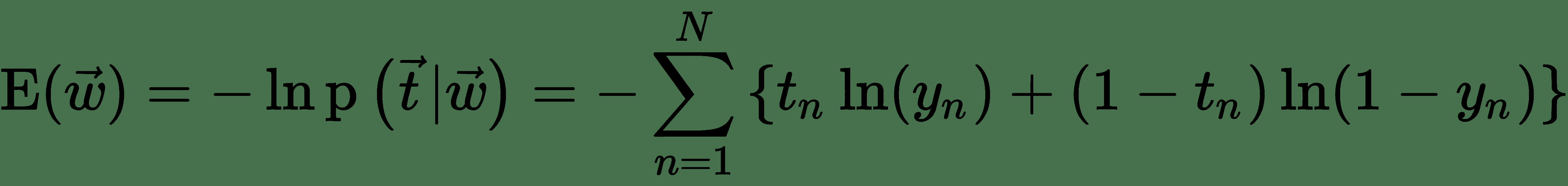 可以通過采用似然性的負算法來定義誤差函數，這給出了交叉熵代價函數：  要學習邏輯神經單元的權重，我們需要關于每個權重的輸出導數。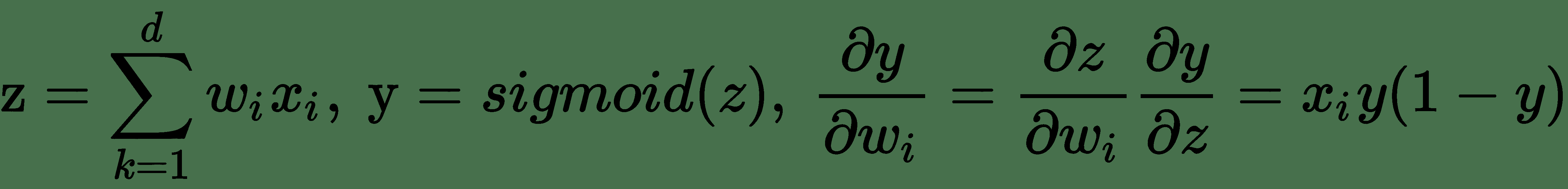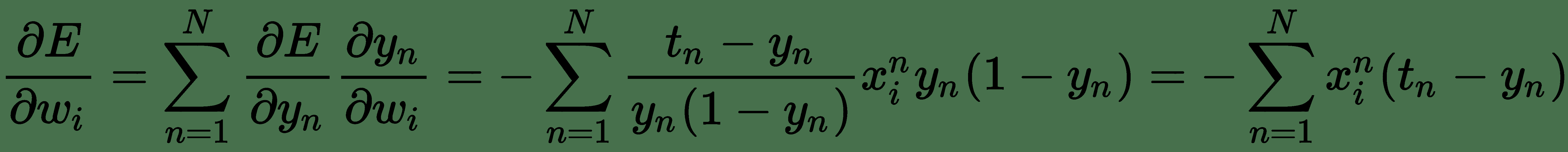 我們將使用導數的*鏈式規則*來導出邏輯單元的誤差導數： 讓：  因此：  就線性單元的平方誤差損失而言，我們發現的導數看起來與導數非常相似，但它們并不相同。 讓我們仔細看一下交叉熵損失，看看它與平方誤差有何不同。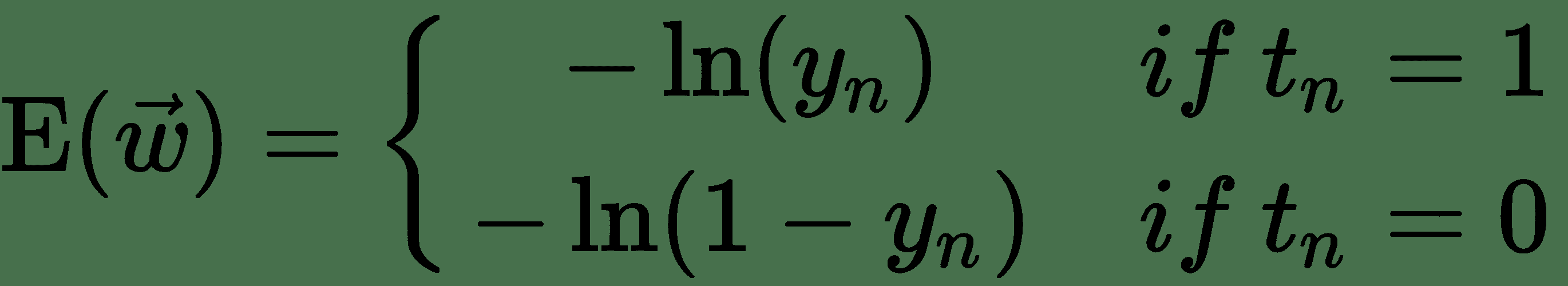 我們可以如下重寫交叉熵損失：  * 因此，對于`t[n] = 1`，`y[n] = 1 => E(w) = 0`，但`y[n] = 0 => E(w) = +∞` * 對于`t[n] = 0`，`y[n] = 1 => E(w) = +∞`，但`y[n] = 0 => E(w) = 0` * 也就是說，如果類別標簽的預測和真實值不同，則該算法將受到很大的懲罰。 現在，讓我們嘗試將*平方誤差損失*與邏輯輸出一起使用。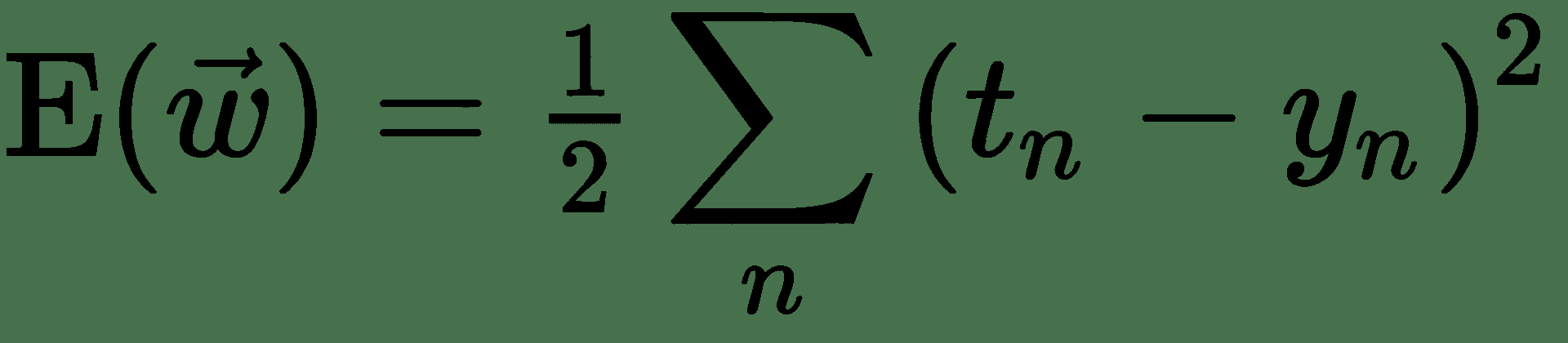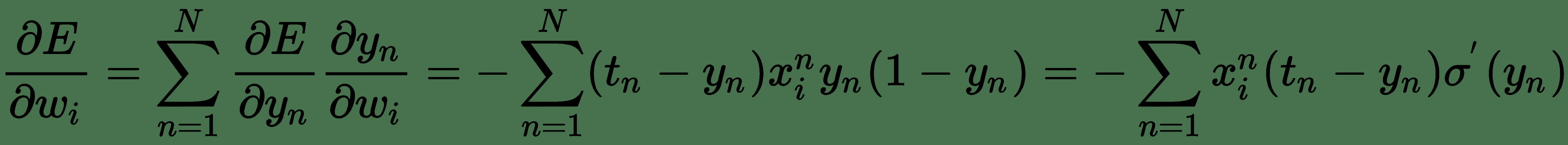 因此，我們的成本函數為：  因此：  該誤差導數直接取決于 Sigmoid 函數`σ'(y[n])`的導數。 現在，當`y[n]`高度負值時，Sigmoid 函數趨于 0；當`y[n]`高度正值時，Sigmoid 函數趨于 1。 從 Sigmoid 曲線的平坦水平區域可以明顯看出，對于`y[n]`的這種值，梯度可以縮小得太小。 因此，即使`t[n]`和`y[n]`不一致，對于這些數據點，平方誤差導數也將具有很小的更新。 也就是說，它們被網絡嚴重錯誤分類。 這稱為**消失梯度問題**。 因此，基于最大似然的交叉熵損失幾乎始終是訓練邏輯單元的首選損失函數。 # 損失函數 損失函數將神經網絡的輸出與訓練中的目標值進行比較，產生一個損失值/分數，以測量網絡的預測與期望值的匹配程度。 在上一節中，我們看到了針對不同任務（例如回歸和二分類）的不同類型損失函數的需求。 以下是一些其他流行的損失函數： * **二元交叉熵**：關于邏輯單元的上一節討論的兩類分類問題的對數損失或交叉熵損失。 * **分類交叉熵**：如果我們有 *K* 類分類問題，那么我們將廣義交叉熵用于 *K* 類。 * **均方誤差**：這是我們討論過幾次的均方和誤差。 這廣泛用于各種回歸任務。 * **平均絕對誤差**：測量一組預測中誤差的平均大小，而不考慮其方向。 這是測試樣本中預測值與實際觀測值之間的絕對差異的平均值。 **平均絕對誤差**（**MAE**）對大誤差賦予相對較高的權重，因為它會平方誤差。 * **平均絕對百分比誤差**：以百分比形式度量誤差的大小。 計算為無符號百分比誤差的平均值。 使用**平均絕對百分比誤差**（**MAPE**）是因為容易理解百分比。 * **鉸鏈損失/平方鉸鏈損失**：鉸鏈損耗用于 SVM。 他們對邊際錯誤分類點的懲罰不同。 它們是克服交叉熵損失的好選擇，并且還可以更快地訓練神經網絡。 對于某些分類任務，更高階的鉸鏈損耗（例如平方鉸損耗）甚至更好。 * **Kullback-Leibler（KL）散度**：KL 散度是一種概率分布與第二個預期概率分布之間如何偏離的度量。 # 數據表示 神經網絡訓練的訓練集中的所有輸入和目標都必須表示為張量（或多維數組）。 張量實際上是將二維矩陣推廣到任意數量的維。 通常，這些是浮點張量或整數張量。 無論原始輸入數據類型是什么（圖像，聲音，文本），都應首先將其轉換為合適的張量表示形式。 此步驟稱為**數據向量化**。 以下是本書中經常使用的不同維度的張量： * **零維張量或標量**：僅包含一個數字的張量稱為零維張量，零維張量或標量。 * **一維張量或向量**：包含數字數組的張量稱為向量或一維張量。 張量的維數也稱為張量的**軸**。 一維張量恰好具有一個軸。 * **矩陣（二維張量）**：包含向量數組的張量是矩陣或二維張量。 矩陣具有兩個軸（由*行*和*列*表示）。 * **三維張量**：通過將一組（相同維度的）矩陣堆疊在一個數組中，我們得到一個三維張量。 通過將三維張量放置在一個數組中，可以創建三維張量。 等等。 在深度學習中，通常我們使用零維到四維張量。 張量具有三個關鍵屬性： * 軸的尺寸或數量 * 張量的形狀，即張量在每個軸上具有多少個元素 * 數據類型 - 是整數張量還是浮點型張量 # 張量示例 以下是在討論遷移學習用例時將經常使用的一些示例張量。 * **時間序列數據**：典型的時間序列數據將具有時間維度，并且該維度將對應于每個時間步的特征。 例如，一天中每小時的溫度和濕度測量是一個時間序列數據，可以用形狀為`(24, 2)`的 2D 張量表示。 因此，數據批量將由 3D 張量表示。 * **圖像數據**：圖像通常具有三個維度：寬度，高度和顏色通道。 因此，可以用 3D 張量表示。 圖像批量由 4D 張量表示，如下圖所示。 * **視頻數據**：視頻由圖像幀組成。 因此，要表示單個視頻，我們還需要一個尺寸。 一幀是彩色圖像，需要三個維度來表示一幀。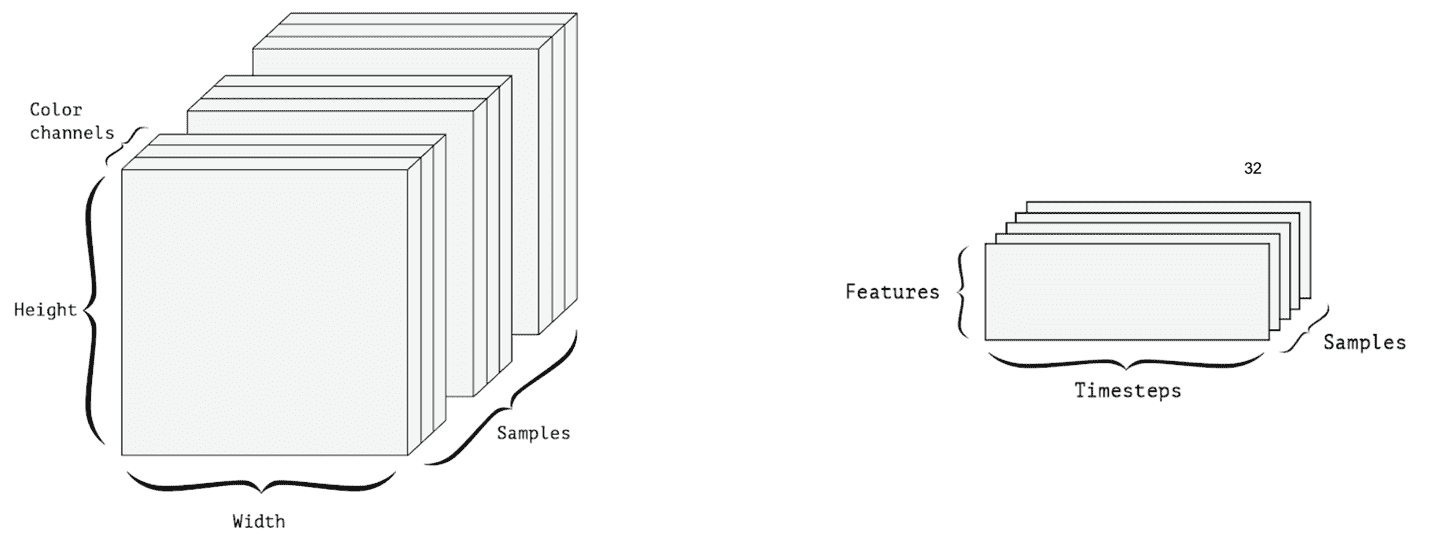 該視頻由形狀（幀，寬度，高度，顏色通道）的 4D 張量表示：  * **作為張量的數據批次**：假設我們有一批 10 張圖像。 諸如 MNIST 數據中的二元圖像可以由 2D 張量表示。 對于一批 10 張圖像，可以用 3D 張量表示。 此 3D 張量的第一個軸（軸 0）稱為**批次尺寸**。 # 張量運算 可以通過一組張量運算來表述用于訓練/測試深度神經網絡的所有計算。 例如，張量的相加，相乘和相減。 以下是本書中一些常用的張量運算： * **逐元素運算**：在深度學習中非常普遍地將函數獨立地應用于張量的所有元素。 例如，將激活函數應用于層中的所有單元。 其他按元素進行的運算包括將基本數學運算符（例如`+`，`-`和`*`）按元素進行對相同形狀的兩個張量進行運算。 * **張量點積**：兩個張量的點積與兩個張量的元素乘積不同。 兩個向量的點積是一個標量，等于兩個向量的元素乘積之和。 矩陣和兼容形狀的向量的點積是向量，而兼容形狀的兩個矩陣的點積是另一個矩陣。 對于具有兼容形狀的兩個矩陣 x，y，我們的意思是要定義點`(x, y)`，我們應具有`x.shape[1] = y.shape[0]`。 * **廣播**：假設我們要添加兩個形狀不同的張量。 這通常出現在神經網絡的每一層。 讓我們以 ReLU 層為例。 ReLU 層可以通過張量操作表示如下：`output = relu(dot(W, input) + b)`。 在這里，我們正在計算權重矩陣與輸入向量`x`的點積。 這將產生一個向量，然后添加一個標量偏差項。 實際上，我們希望將偏置項添加到點積輸出向量的每個元素中。 但是，偏置張量是零維張量，向量是一維。 因此，這里我們需要廣播較小的張量以匹配較大張量的形狀。 廣播涉及兩個步驟：將軸添加到較小的張量以匹配較大張量的尺寸。 然后，重復較小的張量以匹配較大張量的形狀。 我們將通過一個具體示例對此進行說明：令`x`為形狀`(32, 10)`，`y`為形狀`(10)`。 我們要計算`x + y`。 在廣播的第一步之后，我們將軸添加到`y`（較小的張量），并得到形狀為`(1, 10)`的張量`y1`。 為了匹配`x`的尺寸，我們將`y1`重復 32 次，并得到形狀為`(32, 10)`的`y2`張量。 然后，我們計算元素加法`x + y2`。 * **重塑**：張量重塑是沿軸向重新排列張量元素的操作。 重塑的一個簡單示例是轉置 2D 張量。 在矩陣的轉置操作中，*行*和*列*互換。 重塑的另一個例子是拉緊張量。 通過將張量的所有元素沿一個軸放置，可以將多維張量重塑為向量或一維張量。 以下是 TensorFlow 中的一些張量操作實現示例： ```py #EXAMPLE of Tensor Operations using tensorflow. import tensorflow as tf # Initialize 3 constants: 2 vectors, a scalar and a 2D tensor x1 = tf.constant([1,2,3,4]) x2 = tf.constant([5,6,7,8]) b = tf.constant(10) W = tf.constant(-1, shape=[4, 2]) # Elementwise Multiply/subtract res_elem_wise_mult = tf.multiply(x1, x2) res_elem_wise_sub = tf.subtract(x1, x2) #dot product of two tensors of compatable shapes res_dot_product = tf.tensordot(x1, x2, axes=1) #broadcasting : add scalar 10 to all elements of the vector res_broadcast = tf.add(x1, b) #Calculating Wtx res_matrix_vector_dot = tf.multiply(tf.transpose(W), x1) #scalar multiplication scal_mult_matrix = tf.scalar_mul(scalar=10, x=W) # Initialize Session and execute with tf.Session() as sess: output = sess.run([res_elem_wise_mult,res_elem_wise_sub, res_dot_product, res_broadcast,res_matrix_vector_dot, scal_mult_matrix]) print(output) ``` # 多層神經網絡 單層非線性單元對于它可以學習的輸入輸出轉換的能力仍然有限。 可以通過查看 XOR 問題來解釋。 在 XOR 問題中，我們需要一個神經網絡模型來學習 XOR 函數。 XOR 函數采用兩個布爾輸入，如果它們不同則輸出 1，如果輸入相同則輸出 0。 我們可以將其視為輸入模式為`X = {(0, 0), (0, 1), (1, 0), (1, 1)}`的模式分類問題。 第一個和第四個在類 0 中，其他在第 1 類中。讓我們將此問題視為回歸問題，損失為**均方誤差**（**MSE**），并嘗試使用線性單元。 通過分析求解，得出所需權重：`w = (0, 0)`和偏差：`b = 1/2`。 該模型為所有輸入值輸出 0.5。 因此，簡單的線性神經元無法學習 XOR 函數。 解決 XOR 問題的一種方法是使用輸入的不同表示形式，以便線性模型能夠找到解決方案。 這可以通過向網絡添加非線性隱藏層來實現。 我們將使用帶有兩個隱藏單元的 ReLU 層。 輸出是布爾值，因此最適合的輸出神經元是邏輯單元。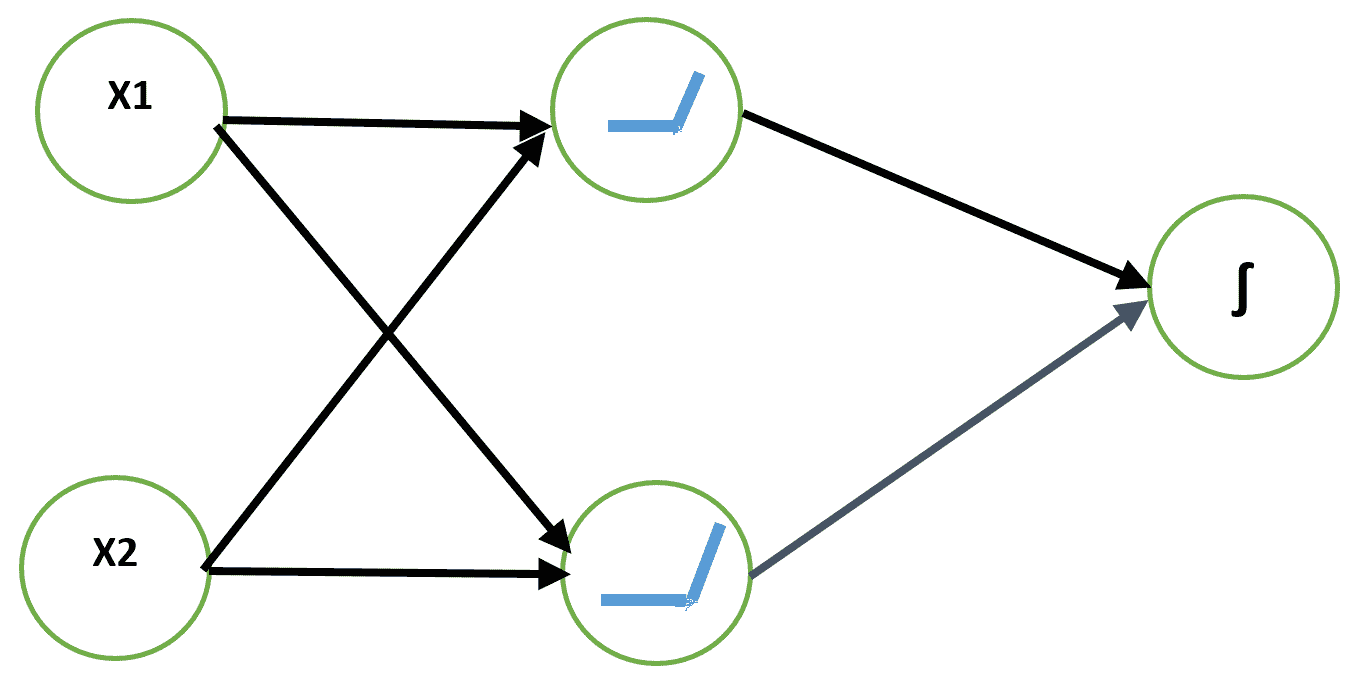 我們可以使用二元交叉熵損失來學習權重：  讓我們使用 SGD 學習此網絡的權重。 以下是 XOR 函數學習問題的`keras`代碼： ```py model_input = Input(shape=(2,), dtype='float32') z = Dense(2,name='HiddenLayer', kernel_initializer='ones')(model_input) z = Activation('relu')(z) #hidden activation ReLu z = Dense(1, name='OutputLayer')(z) model_output = Activation('sigmoid')(z) #Output activation model = Model(model_input, model_output) model.summary() #Compile model with SGD optimization, with learning rate = 0.5 sgd = SGD(lr=0.5) model.compile(loss="binary_crossentropy", optimizer=sgd) #The data set is very small - will use full batch - setting batch size = 4 model.fit(X, y, batch_size=4, epochs=300,verbose=0) #Output of model preds = np.round(model.predict(X),decimals=3) pd.DataFrame({'Y_actual':list(y), 'Predictions':list(preds)}) ``` 前面代碼的輸出如下：  （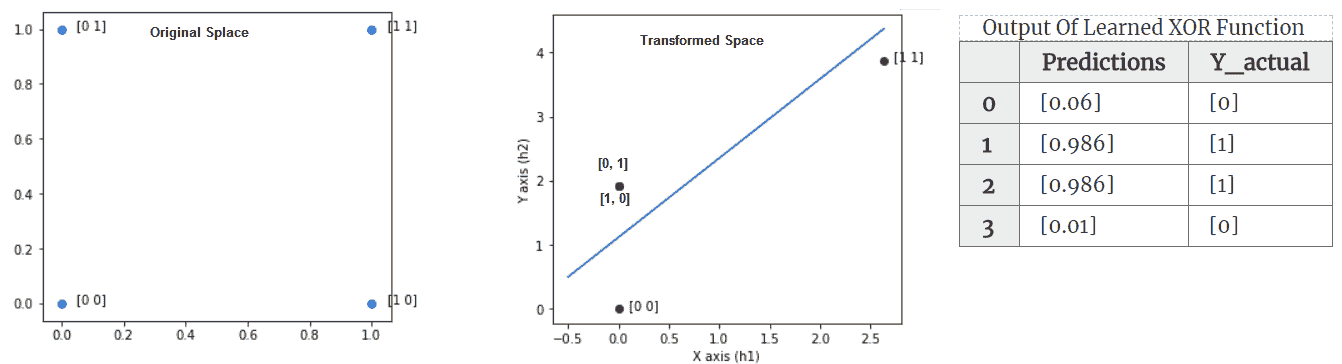左）顯示 4 點的原始空間-顯然沒有行可以將 0 類`{(0, 0), (1, 1)}`與其他類分開。 （中心）顯示隱藏的 ReLU 層學習到的變換空間。 （右）該表顯示了通過該函數獲得的預測值 具有一層隱藏層的神經網絡能夠學習 XOR 函數。 這個例子說明了神經網絡需要非線性隱藏層來做有意義的事情。 讓我們仔細看一下隱藏層學習了哪些輸入轉換，從而使輸出邏輯神經元學習該函數。 在 Keras 中，我們可以從學習的模型中提取中間隱藏層，并使用它來提取傳遞給輸出層之前輸入的轉換。 上圖顯示了如何轉換四個點的輸入空間。 轉換后，可以用一條線輕松地分隔 1 類和 0 類點。 這是為原始空間和變換后的空間生成圖的代碼： ```py import matplotlib.pyplot as plt #Extract intermediate Layer function from Model hidden_layer_output = Model(inputs=model.input, outputs=model.get_layer('HiddenLayer').output) projection = hidden_layer_output.predict(X) #use predict function to extract the transformations ``` ```py #Plotting the transformed input fig = plt.figure(figsize=(5,10)) ax = fig.add_subplot(211) plt.scatter(x=projection[:, 0], y=projection[:, 1], c=('g')) ``` 通過堆疊多個非線性隱藏層，我們可以構建能夠學習非常復雜的非線性輸入輸出轉換的網絡。 # 反向傳播 – 訓練深度神經網絡 為了訓練深層的神經網絡，我們仍然可以使用梯度下降 SGD。 但是，SGD 將需要針對網絡的所有權重計算損失函數的導數。 我們已經看到了如何應用導數鏈式規則來計算邏輯單元的導數。 現在，對于更深的網絡，我們可以逐層遞歸地應用相同的鏈式規則，以獲得與網絡中不同深度處的層對應的權重有關的損失函數的導數。 這稱為反向傳播算法。 反向傳播技術是在 1970 年代發明的，它是一種用于對復雜的嵌套函數或函數的函數進行自動微分的一般優化方法。 但是，直到 1986 年，Rumelhart，Hinton 和 Williams 發表了一篇論文，標題為[《通過反向傳播的誤差學習算法》](https://www.iro.umontreal.ca/~vincentp/ift3395/lectures/backprop_old.pdf)，該算法的重要性已為大型 ML 社區所認可。 反向傳播是最早能夠證明人工神經網絡可以學習良好內部表示的方法之一。 也就是說，它們的隱藏層學習了非平凡的特征。 反向傳播算法是在單個訓練示例上針對每個權重計算誤差導數`dE/dθ`的有效方法。 為了理解反向傳播算法，讓我們首先代表一個帶有計算圖符號的神經網絡。 神經網絡的計算圖將具有節點和有向邊，其中節點代表變量（張量），邊代表連接到下一個變量的變量的運算。 如果`y = f(x)`，則變量`x`通過有向邊連接到`y`，對于某些函數`f`。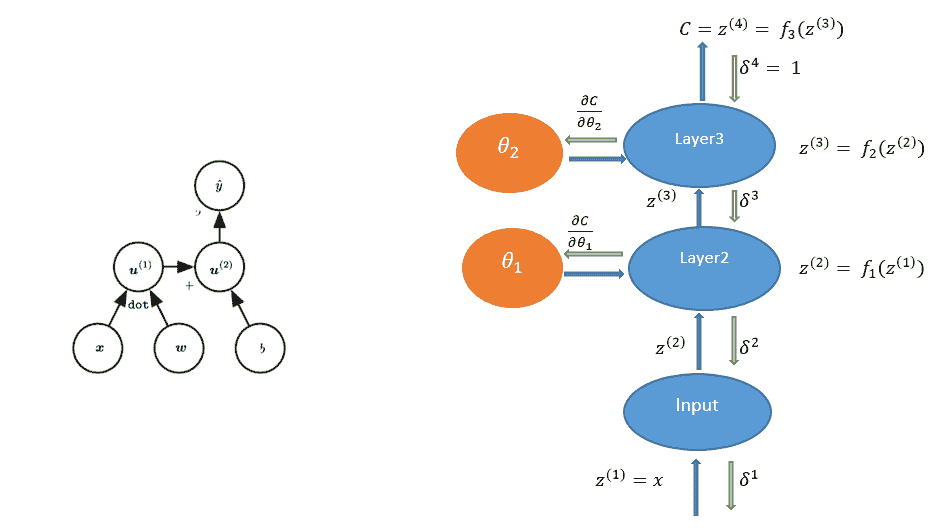 例如，邏輯單元的圖形可以表示如下：  （左）邏輯回歸作為計算圖。 （右）三層網絡計算圖的 BP 算法信息流 我們用`u[1], u[2], ..., u[n]`表示計算節點。 另外，我們按順序排列節點，以便可以一個接一個地計算它們。 `u[n]`是一個標量-損失函數。 讓我們用節點`θ[k]`表示網絡的參數或權重。 要應用梯度下降，我們需要計算所有導數`?u^n/?θ[k]`。 可以通過遵循從輸入節點到最終節點`?u^n`的計算圖中的有向路徑來計算該圖的正向計算。 這稱為**前向傳播**。 由于圖中的節點為張量，因此要計算偏導數`?u^n/?θ[k]`，將使用多個變量函數的導數鏈式規則，該規則由雅可比矩陣與梯度的乘積表示。 反向傳播算法涉及一系列這樣的雅可比梯度積。 反向傳播算法表示如下： 1. 給定輸入向量`X = {x[n]}`，目標向量`Y = {t[n]}`，用于測量網絡誤差的成本函數`C`以及網絡的初始權重集，以計算網絡的前向通過并計算損耗`C` 2. 向后傳遞-對于每個訓練示例`(x[n], t[n])`，針對每個層參數/權重計算損耗的導數`C`-此步驟討論如下： 1. 通過對輸入目標對或它們的小批量的所有梯度求平均值來組合各個梯度 2. 更新每個參數`Δθ[l] = -α · ?C/?θ[l]`，`α`為學習率 我們將使用完全連接的三層神經網絡解釋*反向傳播*。 上圖顯示了為此的計算圖。 令`z(i)`表示圖中的計算節點。 為了執行反向傳播，導數`?C/?z(i)`的計算將與正向傳遞的反向順序完全相同。 這些由向下箭頭指示。 讓我們表示關于層`l`的輸入`z(l)`的成本函數的導數`δ(l)`。 對于最頂層，讓`δ(4) = 1`。 為了遞歸計算，讓我們考慮一個單層。 一層具有輸入`z(l)`和輸出`z(l+1)`。 同樣，該層將接受輸入`δ(l + 1)`并產生`δ(l)`和`?C/?θ[l]`。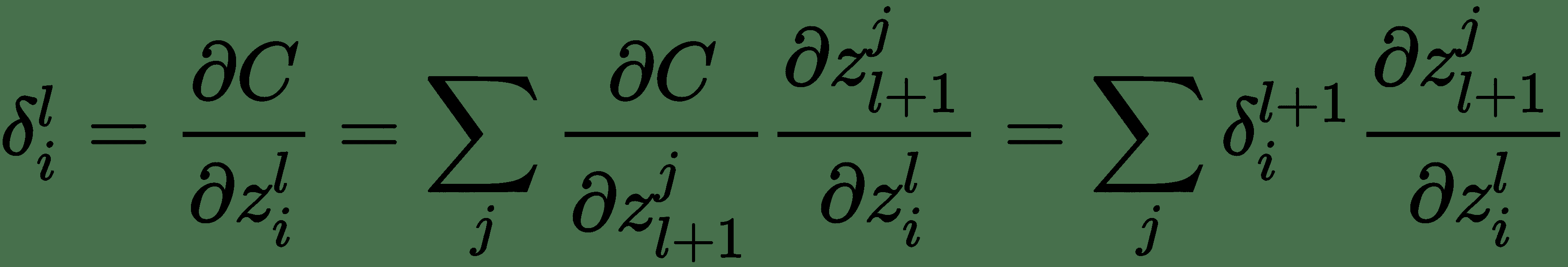 對于層`l`：  `i`代表梯度`δ(l)[i]`的第`i`個分量。 因此，我們得出了用于計算反向消息的遞歸公式。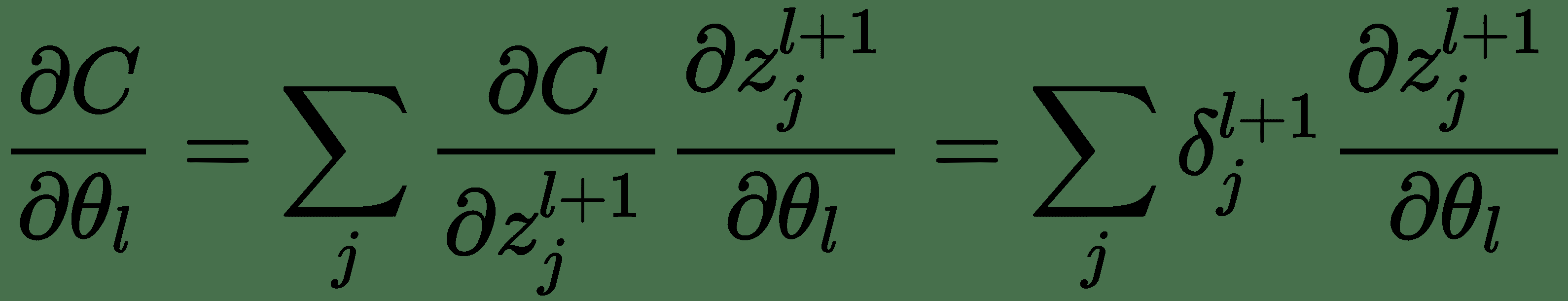 使用這些，我們還可以計算關于模型參數的成本導數，如下所示：  反向傳播算法在計算圖中相對于其祖先`x`，計算標量成本函數`z`的梯度。 該算法開始于計算關于其本身的成本`z`的導數`?z/?z = 1`。 可以通過將當前梯度乘以產生`z`的運算的雅可比行列式來計算關于`z`父級的梯度。 我們一直向后遍歷計算圖并乘以雅可比行列式，直到達到輸入`x`為止。 # 神經網絡學習中的挑戰 通常，優化是一項非常困難的任務。 在本節中，我們討論了用于訓練深度模型的優化方法所涉及的一些常見挑戰。 了解這些挑戰對于評估神經網絡模型的訓練表現并采取糾正措施以緩解問題至關重要。 # 病態條件 矩陣的條件數是最大奇異值與最小奇異值之比。 如果條件數非常高，則矩陣是病態的，通常表示最低的奇異值比最高的奇異值小幾個數量級，并且矩陣的行彼此高度相關。 這是優化中非常普遍的問題。 實際上，這甚至使凸優化問題也難以解決。 通常，神經網絡會出現此問題，這會導致 SGD 卡住，即，盡管存在很強的梯度，學習也會變得非常緩慢。 對于具有良好條件數（接近 1）的數據集，誤差輪廓幾乎是圓形的，并且負梯度始終筆直指向誤差表面的最小值。 對于條件差的數據集，誤差表面在一個或多個方向上相對平坦，而在其他方向上則強烈彎曲。 對于復雜的神經網絡，可能無法通過解析找到 Hessian 和病態效應。 但是，可以通過在訓練周期內繪制平方梯度范數和`g^T H[g]`來繪制圖表，以監控疾病的影響。 讓我們考慮我們要優化的`f(x)`函數的二階泰勒級數逼近。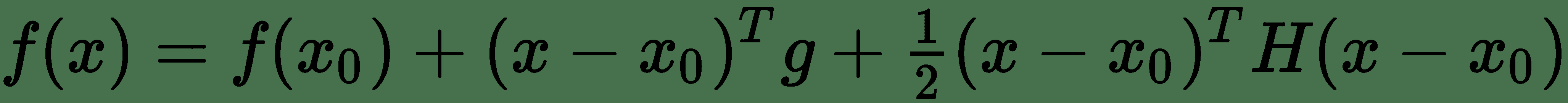`z[0]`點的泰勒級數由下式給出：  其中`g`是梯度向量， `H`是`f(x)`在`x[0]`時的 Hessian。 如果`ε`是我們使用的學習率，則根據梯度下降的新點為`x[0] - ε[g]`。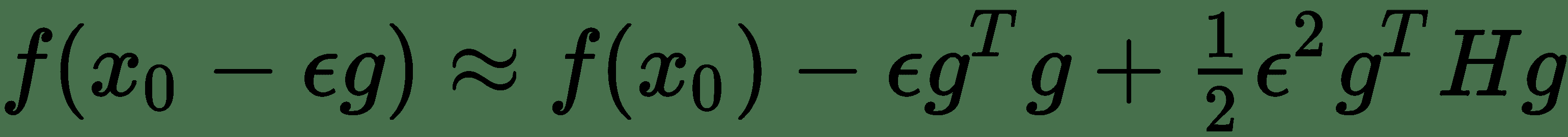 將其替換為 Taylor 系列展開式，我們得到：  注意，如果`-ε g^t g + ?ε^2 g^T H[g] > 0`，則與`x[0]`相比，新點的函數值會增加。 同樣，在存在強梯度的情況下，我們將具有較高的平方梯度范數`||g||^2 = g^T g`，但同時，如果其他數量為`g^T H[g]`增長一個數量級，那么我們將看到`f(x)`的下降速度非常緩慢。 但是，如果此時可以縮小學習率`ε`，則可能會在某種程度上使這種影響無效，因為`g^T H[g]`數量乘以`ε^2`。 可以通過在訓練周期繪制平方梯度范數和`g^T H[g]`來監測疾病的影響。 我們在*熱板*中看到了如何計算梯度范數的示例。 # 局部最小值和鞍點 DNN 模型實質上可以保證具有極大數量的局部最小值。 如果局部最小值與全局最小值相比成本較高，則可能會出現問題。 長期以來，人們一直認為，由于存在這樣的局部極小值，神經網絡訓練受到了困擾。 這仍然是一個活躍的研究領域，但是現在懷疑對于 DNN，大多數局部最小值具有較低的成本值，沒有必要找到全局最小值，而是在權重空間中具有足夠低的成本函數值。 可以通過監視梯度范數來檢測強局部極小值的存在。 如果梯度范數減小到很小的數量級，則表明存在局部極小值。 鞍點是既不是最大值也不是最小值的點，而是被平坦區域圍繞，該平坦區域的一側目標函數值增大，而另一側目標函數減小。 由于該平坦區域，梯度變得非常小。 然而，已經觀察到，憑經驗梯度下降迅速逃離了這些區域。 # 懸崖和梯度爆炸 高度非線性 DNN 的目標函數具有非常陡峭的區域，類似于懸崖，如下圖所示。 在極陡峭的懸崖結構的負梯度方向上移動會使權重移得太遠，以致我們完全跳下懸崖結構。 因此，在我們非常接近的時候錯過了極小值。 因此，取消了為達到當前解決方案所做的許多工作：  解釋何時需要裁剪梯度范數 我們可以通過裁剪梯度來避免梯度下降中的此類不良動作，也就是說，設置梯度幅度的上限。 我們記得梯度下降是基于函數的一階泰勒近似。 這種近似在計算梯度的點附近的無窮小區域中保持良好。 如果我們跳出該區域，成本函數可能開始增加或向上彎曲。 因此，我們需要限制移動的時間。 梯度仍然可以給出大致正確的方向。 必須將更新選擇為足夠小，以避免越過向上的彎曲。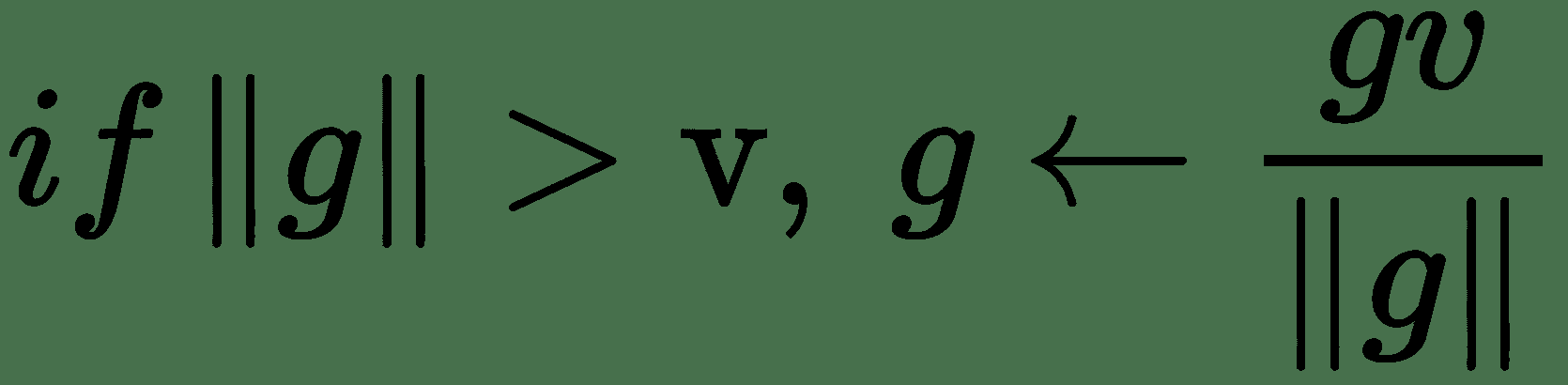 一種實現此目的的方法是通過設置標準的上限閾值來限制**梯度邊界**：  在 Keras 中，可以如下實現： ```py #The parameters clipnorm and clipvalue can be used with all optimizers #to control gradient clipping: from keras import optimizers # All parameter gradients will be clipped to max norm of 1.0 sgd = optimizers.SGD(lr=0.01, clipnorm=1.) #Similarly for ADAM optmizer adam = optimizers.Adam(clipnorm=1.) ``` # 初始化 – 目標的本地和全局結構之間的不良對應關系 要啟動數值優化算法（例如 SGD），我們需要初始化權重。 如果我們具有目標函數，如下圖所示，通過進行 SGD 建議的局部移動，我們將浪費大量時間，如果我們從真正的極小值所在的山側開始。 在這種情況下，目標函數的局部結構不會給出任何關于最小值位于何處的提示。 可以通過適當的初始化來避免這種情況。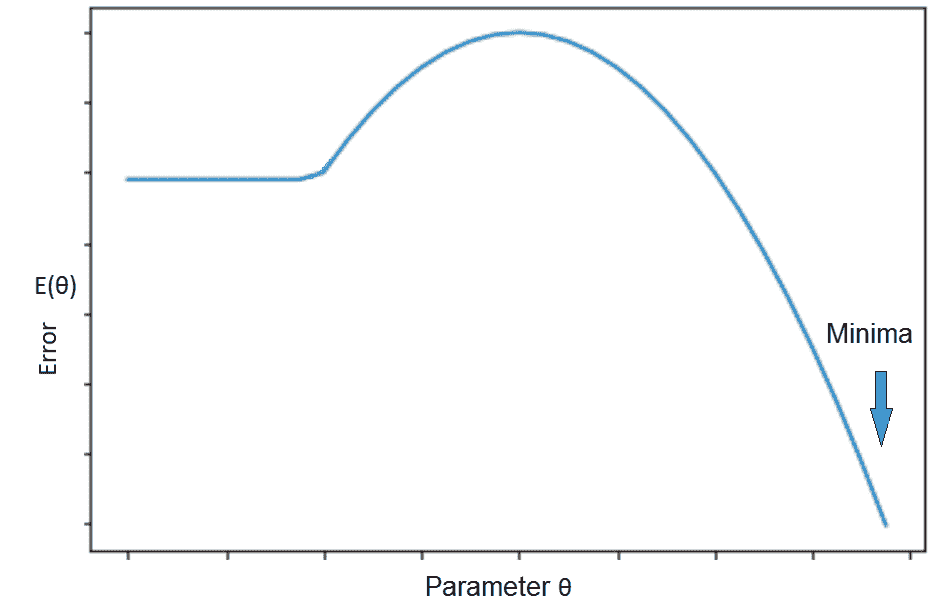 如果我們可以在山的另一側的某個位置啟動 SGD，則優化會快得多：  解釋初始化誤差的情況以及對基于梯度的優化的影響 # 不精確的梯度 大多數優化算法都是基于這樣的假設，即我們在給定點具有已知的精確梯度。 但是，實際上我們只對梯度有一個估計。 這個估計有多好？ 在 SGD 中，批次大小會極大地影響隨機優化算法的行為，因為它確定了梯度估計的方差。 總之，可以通過以下四個技巧來解決神經網絡訓練中面臨的不同問題： * 選擇合適的學習率，可能是每個參數的自適應學習率 * 選擇合適的批次大小 - 梯度估計取決于此 * 選擇權重的良好初始化 * 為隱藏層選擇正確的激活函數 現在，讓我們簡要討論一下各種啟發式方法/策略，這些方法使學習 DNN 切實可行并繼續使深度學習取得巨大成功。 # 模型參數的初始化 以下是初始點的選擇如何影響深度神經網絡的迭代學習算法的表現： * 初始點可以確定學習是否會收斂 * 即使學習收斂，收斂的速度也取決于起始點 * 成本相似的初始點可能具有不同的泛化誤差 初始化算法主要是啟發式的。 良好初始化的全部要點是可以以某種方式使學習更快。 初始化的重要方面之一是*破壞初始權重集對隱藏層單元的對稱性*。 如果以相同的權重對其進行初始化，則在網絡相同級別上具有相同激活函數的兩個單元將被同等更新。 多個單元保留在隱藏層中的原因是它們應該學習不同的特征。 因此，獲得同等更新不會影響其他特征的學習。 打破對稱性的一種簡單方法是使用隨機初始化-從高斯或均勻分布中采樣。 模型中的偏差參數可以通過啟發式選擇常量。 選擇權重的大小取決于優化和正則化之間的權衡。 正則化要求權重不應太大-這可能導致不良的泛化表現。 優化需要權重足夠大，才能成功地通過網絡傳播信息。 # 啟發式初始化 讓我們考慮具有`m`輸入和`n`輸出單元的密集層： 1. 從均勻分布`[-1/√m, 1/√m]`中采樣每個權重。 2. 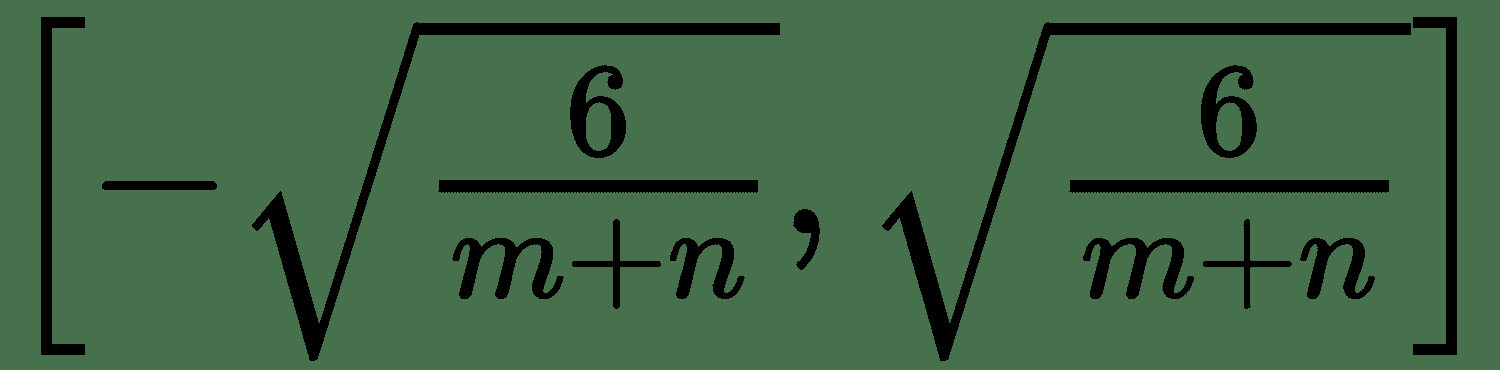Glorot 和 Bengio 建議使用統一分布初始化的規范化版本：  它被設計為在每一層中具有相同的梯度變化，稱為 **Glorot Uniform** 。 3. 從平均值為 0 且方差為`√(2/(m+n))`的正態分布中采樣每個權重。 這類似于 Glorot Uniform，稱為 **Glorot Normal**。 4. 對于非常大的層，單個權重將變得非常小。 要解決此問題，另一種方法是僅初始化 *k* 非零權重。 這稱為**稀疏初始化**。 5. 將權重初始化為隨機正交矩陣。 可以在初始權重矩陣上使用 Gram-Schmidt 正交化。 初始化方案也可以視為神經網絡訓練中的超參數。 如果我們有足夠的計算資源，則可以評估不同的初始化方案，我們可以選擇具有最佳泛化表現和更快的收斂速度的方案。 # SGD 的改進 近年來，已提出了不同的優化算法，這些算法使用不同的方程式更新模型的參數。 # 動量法 成本函數可能具有高曲率和較小但一致的梯度的區域。 這是由于 Hessian 矩陣的條件不佳以及隨機梯度的方差。 SGD 在這些地區可能會放慢很多速度。 動量算法會累積先前梯度的**指數加權移動平均值**（**EWMA**），并朝該方向移動，而不是 SGD 建議的局部梯度方向。 指數加權由超參數`α ∈ [0, 1)`控制，該超參數確定先前梯度的影響衰減的速度。 動量法通過組合相反符號的梯度來阻尼高曲率方向上的振蕩。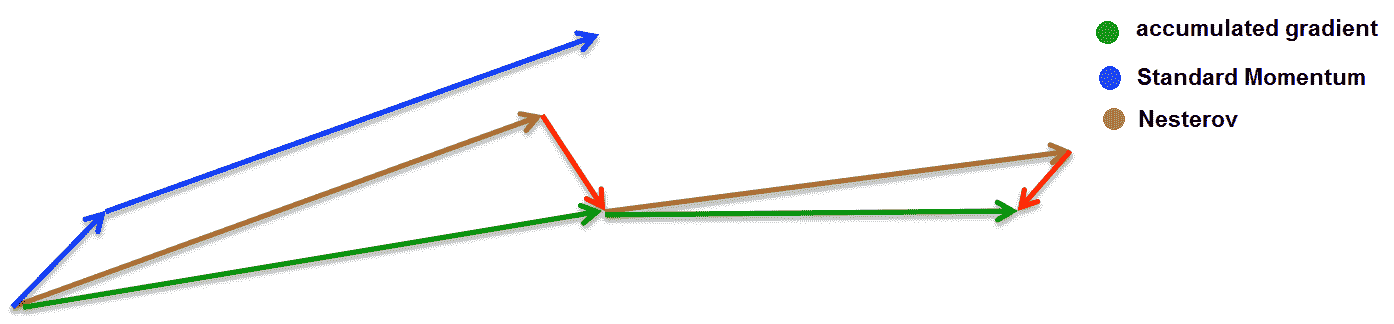 # Nesterov 動量 Nesterov 動量是動量算法的一種變體，僅在計算梯度時與動量方法不同。 標準動量法首先在當前位置計算梯度，然后在累積梯度的方向上發生較大的跳躍。 涅斯特羅夫動量首先沿先前累積的梯度的方向躍升，然后計算新點的梯度。 通過再次采用所??有先前梯度的 EWMA 來校正新梯度：  # 自適應學習率 – 每個連接均獨立 在前面的方法中，將相同的學習率應用于所有參數更新。 由于數據稀疏，我們可能想在不同程度上更新參數。 諸如 AdaGrad，AdaDelta，RMSprop 和 Adam 之類的自適應梯度下降算法通過保持每個參數的學習率，提供了經典 SGD 的替代方法。 # AdaGrad AdaGrad 算法通過按與先前所有梯度的平方和值的平方根成比例的方式將它們成反比例縮放來調整每個連接的學習率。 因此，在誤差表面的平緩傾斜方向上進行了較大的移動。 但是，從一開始就采用這種技巧可能會導致某些學習率急劇下降。 但是，AdaGrad 在一些深度學習任務上仍然表現出色。 # RMSprop RMSprop 通過采用先前平方梯度的 EWMA 來修改 AdaGrad 算法。 它具有移動平均參數`ρ`，它控制移動平均的長度和比例。 這是深度神經網絡訓練最成功的算法之一。 # Adam **自適應力矩**（**Adam**）。 它充分利用了基于動量的算法和自適應學習率算法，并將它們組合在一起。 在此，動量算法應用于由 RMSprop 計算的重新縮放的梯度。 # 神經網絡中的過擬合和欠擬合 與其他任何 ML 訓練一樣，用于訓練深度學習模型的數據集也分為訓練，測試和驗證。 在模型的迭代訓練期間，通常，驗證誤差比訓練誤差略大。 如果測試誤差和驗證誤差之間的差距隨著迭代的增加而增加，則是**過擬合**的情況。 如果訓練誤差不再減小到足夠低的值，我們可以得出結論，該模型是**欠擬合**的。 # 模型容量 模型的能力描述了模型可以建模的輸入輸出關系的復雜性。 也就是說，在模型的假設空間中允許有多大的函數集。 例如，可以將線性回歸模型推廣為包括多項式，而不只是線性函數。 這可以通過在構建模型時將 *x* 的 *n* 積分乘以 *x* 作為積分來完成。 還可以通過向網絡添加多個隱藏的非線性層來控制模型的容量。 因此，我們可以使神經網絡模型更寬或更深，或兩者同時進行，以增加模型的容量。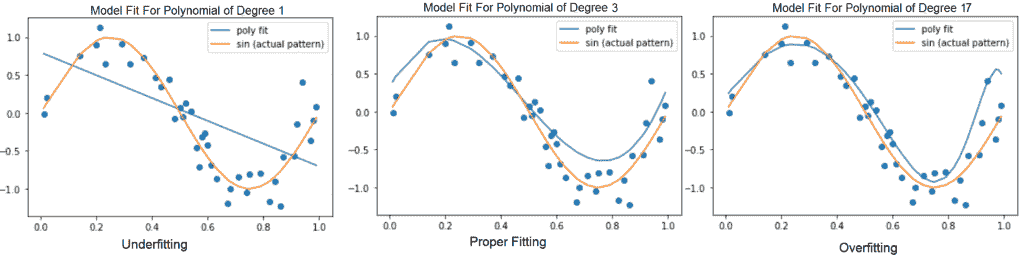 但是，在模型容量和模型的泛化誤差之間需要權衡：  （左）：線性函數根據數據擬合而擬合。 （中）：適合數據的二次函數可以很好地推廣到看不見的點 （右）適合數據的次數為 9 的多項式存在過擬合的問題 具有極高容量的模型可能通過訓練集中的學習模式而過擬合訓練集，而訓練模式可能無法很好地推廣到看不見的測試集。 而且，它非常適合少量的訓練數據。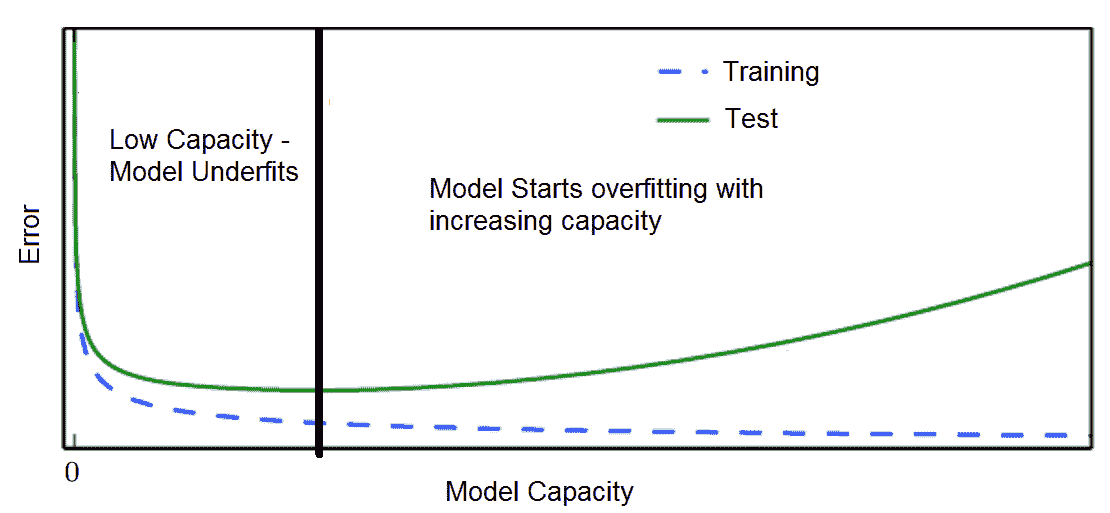 另一方面，低容量的模型可能難以適應訓練集：  在訓練和驗證損失方面過擬合/欠擬合 # 如何避免過擬合 - 正則化 過擬合是 ML 中的核心問題。 對于神經網絡，開發了許多策略來避免過擬合并減少泛化誤差。 這些策略統稱為**正則化**。 # 權重共享 權重共享意味著同一組權重在網絡的不同層中使用，因此我們需要優化的參數更少。 在一些流行的深度學習架構中可以看到這一點，例如暹羅網絡和 RNN。 在幾層中使用共享權重可以通過控制模型容量來更好地推廣模型。 反向傳播可以輕松合并線性權重約束，例如權重共享。 CNN 中使用了另一種權重分配方式，其中與完全連接的隱藏層不同，卷積層在局部區域之間具有連接。 在 CNN 中，假設可以將要由網絡處理的輸入（例如圖像或文本）分解為具有相同性質的一組局部區域，因此可以使用相同的一組轉換來處理它們。 是，共享權重。 RNN 可以被視為前饋網絡，其中每個連續的層共享相同的權重集。 # 權重衰減 可以看到，像前面示例中的多項式一樣，過擬合模型的權重非常大。 為了避免這種情況，可以將罰分項`Ω`添加到目標函數中，這將使權重更接近原點。 因此，懲罰項應該是權重范數的函數。 同樣，可以通過乘以超參數`α`來控制懲罰項的效果。 因此我們的目標函數變為：`E(w) + αΩ(w)`。 常用的懲罰條款是： * **L2 正則化**：懲罰項由`Ω = 1/2 · ||w||^2`給出。 在回歸文獻中，這稱為**嶺回歸**。 * **L1 正則化**：懲罰項由`Ω = ||w||[1] = Σ[i](w[i])`給出。 這稱為 **LASSO 回歸**。 L1 正則化導致稀疏解； 也就是說，它會將許多權重設置為零，因此可以作為回歸問題的良好特征選擇方法。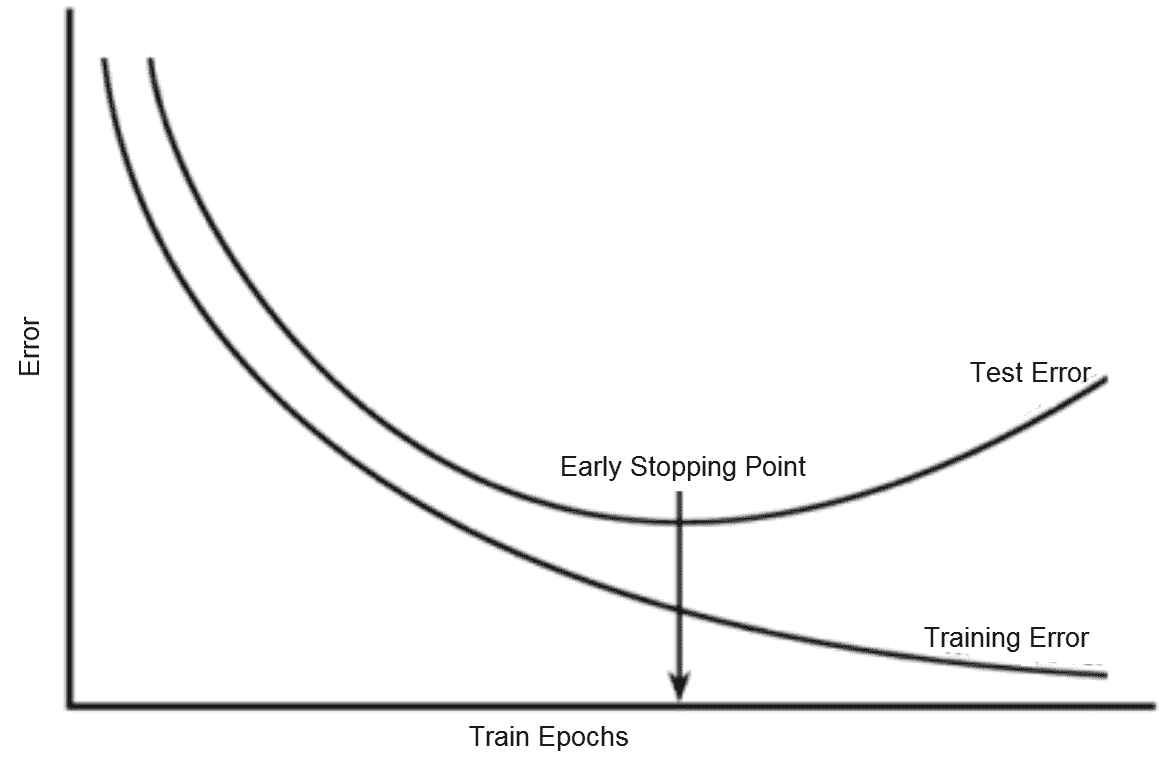 # 早期停止 隨著對大型神經網絡的訓練的進行，訓練誤差會隨著時間的推移而穩步減少，但如下圖所示，驗證集誤差開始增加，超出了某些迭代：  提前停止：訓練與驗證誤差 如果在驗證誤差開始增加的時候停止訓練，我們可以建立一個具有更好泛化表現的模型。 這稱為**提前停止**。 它由耐心超參數控制，該參數設置了中止訓練之前觀察增加的驗證集誤差的次數。 提前停止可以單獨使用，也可以與其他正則化策略結合使用。 # 丟棄法 丟棄法是一種在深度神經網絡中進行正則化的計算廉價但功能強大的方法。 它可以分別應用于輸入層和隱藏層。 通過在正向傳遞過程中將節點的輸出設置為零，丟棄法隨機掩蓋了一部分節點的輸出。 這等效于從層中刪除一部分節點，并創建一個具有更少節點的新神經網絡。 通常，在輸入層上會刪除 0.2 個節點，而在隱藏層中最多會刪除 0.5 個節點。 **模型平均**（集成方法）在 ML 中被大量使用，通過組合各種模型的輸出來減少泛化誤差。 套袋是一種整體方法，其中通過從訓練集中替換并隨機抽樣來構建 *k* 不同的數據集，并在每個模型上訓練單獨的 *k* 模型。 特別地，對于回歸問題，模型的最終輸出是 *k* 模型的輸出的平均值。 還有其他組合策略。 還可以將丟棄視為一種模型平均方法，其中通過更改應用了丟棄的基本模型的各個層上的活動節點數來創建許多模型。 # 批量標準化 在 ML 中，通常的做法是先縮放并標準化輸入的訓練數據，然后再將其輸入模型進行訓練。 對于神經網絡而言，縮放也是預處理步驟之一，并且已顯示出模型表現的一些改進。 在將數據饋送到隱藏層之前，我們可以應用相同的技巧嗎？ 批量規范化基于此思想。 它通過減去激活的最小批量平均值`μ`并除以最小批量標準差`σ`來歸一化前一層的激活。 在進行預測時，我們一次可能只有一個示例。 因此，不可能計算批次均值`μ`和批次`σ`。 將這些值替換為訓練時收集的所有值的平均值。 # 我們需要更多數據嗎？ 使神經模型具有更好的概括性或測試表現的最佳方法是通過訓練它獲得更多數據。 實際上，我們的訓練數據非常有限。 以下是一些用于獲取更多訓練數據的流行策略： * **模擬合成一些訓練樣本**：生成假訓練數據并不總是那么容易。 但是，對于某些類型的數據，例如圖像/視頻/語音，可以將轉換應用于原始數據以生成新數據。 例如，可以平移，旋轉或縮放圖像以生成新的圖像樣本。 * **帶噪聲的訓練**：將受控隨機噪聲添加到訓練數據是另一種流行的數據增強策略。 噪聲也可以添加到神經網絡的隱藏層中。 # 神經網絡的超參數 神經網絡的架構級參數，例如隱藏層數，每個隱藏層的單元數，以及與訓練相關的參數，例如學習率，優化器算法，優化器參數-動量，L1/L2 正則化器和丟棄法統稱為神經網絡的**超參數**。 神經網絡的權重稱為神經網絡的**參數**。 一些超參數影響訓練算法的時間和成本，而一些影響模型的泛化表現。 # 自動超參數調整 開發了多種用于超參數調整的方法。 但是，對于大多數參數，需要為每個超參數指定一個特定范圍的值。 可以通過了解它們對模型容量的影響來設置大多數超參數。 # 網格搜索 網格搜索是對超參數空間的手動指定子集的詳盡搜索。 網格搜索算法需要表現指標，例如交叉驗證誤差或驗證集誤差，以評估最佳可能參數。 通常，網格搜索涉及選擇對數刻度的參數。 例如，可以從集合`{50, 100, 200, 500, 1000，...}`中選擇在集合`{0.1, 0.01, 0.001, 0.0001}`內獲得的學習率或多個隱藏單元。 網格搜索的計算成本隨著超參數的數量呈指數增長。 因此，另一種流行的技術是隨機網格搜索。 隨機搜索從所有指定的參數范圍中對參數采樣固定次數。 當我們具有高維超參數空間時，發現這比窮舉搜索更有效。 更好，因為可能存在一些不會顯著影響損耗的超參數。 # 總結 在本章中，我們涉及了深度學習的基礎知識。 我們真的贊揚您為實現這一目標所做的努力！ 本章的目的是向您介紹與深度學習領域有關的核心概念和術語。 我們首先簡要介紹了深度學習，然后介紹了當今深度學習領域中流行的框架。 還包括詳細的分步指南，用于設置您自己的深度學習環境，以在 GPU 上開發和訓練大規模深度學習模型。 最后，我們涵蓋了圍繞神經網絡的基本概念，包括線性和非線性神經元，數據表示，鏈式規則，損失函數，多層網絡和 SGD。 還討論了神經網絡中的學習挑戰，包括圍繞局部極小值和梯度爆炸的常見警告。 我們研究了神經網絡中過擬合和欠擬合的問題，以及處理這些問題的策略。 然后，我們介紹了神經網絡單元的流行初始化啟發法。 除此之外，我們還探索了一些更新的優化技術，它們是對香草 SGD 的改進，其中包括 RMSprop 和 Adam 之類的流行方法。 在下一章中，我們將探討深度學習模型周圍的各種架構，這些架構可用于解決不同類型的問題。