# 七、無監督學習
到目前為止,我們在本書中涵蓋的所有模型都是基于監督學習范式的。 訓練數據集包括輸入和該輸入的所需標簽。 相反,本章重點介紹無監督的學習范式。 本章將包括以下主題:
* 主成分分析
* K 均值聚類
* 自組織圖
* 受限玻爾茲曼機
* 使用 RBM 的推薦系統
* 用于情感檢測的 DBN
# 介紹
在機器學習中,存在三種不同的學習范式:監督學習,無監督學習和強化學習。
在**監督學習**(也稱為與老師一起學習)中,向網絡提供輸入和各自所需的輸出。 例如,在 MNIST 數據集中,手寫數字的每個圖像都有一個標簽,表示與之關聯的數字值。
在**強化學習**(也稱為與批評家學習)中,沒有為網絡提供所需的輸出; 相反,環境會提供獎勵或懲罰方面的反饋。 當其輸出正確時,環境獎勵網絡,而當輸出不正確時,環境對其進行懲罰。
在**無監督學習**(也稱為無老師學習)中,沒有向網絡提供有關其輸出的信息。 網絡接收輸入,但是既不提供期望的輸出,也不提供來自環境的獎勵; 網絡自己學習輸入的隱藏結構。 無監督學習非常有用,因為正常情況下可用的數據沒有標簽。 它可以用于模式識別,特征提取,數據聚類和降維等任務。 在本章和下一章中,您將學習基于無監督學習的不同機器學習和 NN 技術。
# 主成分分析
**主成分分析**(**PCA**)是用于降維的最流行的多元統計技術。 它分析了由幾個因變量組成的訓練數據,這些因變量通常是相互關聯的,并以一組稱為**主成分**的新正交變量的形式從訓練數據中提取重要信息。 我們可以使用兩種方法執行 PCA -- **特征值分解**或**奇異值分解**(**SVD**)。
# 準備
PCA 將`n`維輸入數據還原為`r`維輸入數據,其中`r < n`。 簡單來說,PCA 涉及平移原點并執行軸的旋轉,以使其中一個軸(主軸)與數據點的差異最小。 通過執行此變換,然后以高方差落下(刪除)正交軸,可以從原始數據集中獲得降維數據集。 在這里,我們采用 SVD 方法降低 PCA 尺寸。 考慮`X`,`n`維數據,具有`p`個點`X[p,n]`。 任何實數(`p × n`)矩陣都可以分解為:
`X = U ∑ V^T`
在這里, `U`和`V`是正交矩陣(即`U · U^T = V^T · V = E`),大小分別為`p × n`和`n × n`。 `∑`是大小為`n × n`的對角矩陣。 接下來,將`∑`矩陣切成`r`列,得到`∑[r]`; 使用`U`和`V`,我們找到了降維數據點`Y[r]`:
`Y[r] = U ∑[r]`
[此處提供的代碼已從以下 GitHub 鏈接進行改編](https://github.com/eliorc/Medium/blob/master/PCA-tSNE-AE.ipynb)
# 操作步驟
我們按以下步驟進行操作:
1. 導入所需的模塊。 我們肯定會使用 TensorFlow; 我們還需要`numpy`進行一些基本矩陣計算,并需要`matplotlib`,`mpl_toolkit`和`seaborn`進行繪圖:
```py
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns
%matplotlib inline
```
2. 我們加載數據集-我們將使用我們最喜歡的 MNIST 數據集:
```py
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/")
```
3. 我們定義了一個`TF_PCA`類,它將實現我們的所有工作。 該類的初始化如下:
```py
def __init__(self, data, dtype=tf.float32):
self._data = data
self._dtype = dtype
self._graph = None
self._X = None
self._u = None
self._singular_values = None
self._sigma = None)
```
4. 給定輸入數據的 SVD 用`fit`方法計算。 該方法定義了計算圖,并執行該計算圖以計算奇異值和正交矩陣`U`。需要`self.data`來輸入占位符`self._X`。 `tf.svd`以降序返回形狀`[..., p]`的`s`(`singular_values`)。 我們使用`tf.diag`將其轉換為對角矩陣:
```py
def fit(self):
self._graph = tf.Graph()
with self._graph.as_default():
self._X = tf.placeholder(self._dtype, shape=self._data.shape)
# Perform SVD
singular_values, u, _ = tf.svd(self._X)
# Create sigma matrix
sigma = tf.diag(singular_values)
with tf.Session(graph=self._graph) as session:
self._u, self._singular_values, self._sigma = session.run([u, singular_values, sigma], feed_dict={self._X: self._data})
```
5. 現在我們有了`sigma`矩陣,正交`U`矩陣和奇異值,我們通過定義`reduce`方法來計算降維數據。 該方法需要兩個輸入參數之一`n_dimensions`或`keep_info`。 `n_dimensions`參數表示我們要保留在降維數據集中的維數。 另一方面,`keep_info`參數確定我們要保留的信息的百分比(值為 0.8 表示我們要保留 80% 的原始數據)。 該方法創建一個切片 Sigma 矩陣的圖,并計算降維數據集`Y[r]`:
```py
def reduce(self, n_dimensions=None, keep_info=None):
if keep_info:
# Normalize singular values
normalized_singular_values = self._singular_values / sum(self._singular_values)
# information per dimension
info = np.cumsum(normalized_singular_values) # Get the first index which is above the given information threshold
it = iter(idx for idx, value in enumerate(info) if value >= keep_info)
n_dimensions = next(it) + 1
with self.graph.as_default():
# Cut out the relevant part from sigma
sigma = tf.slice(self._sigma, [0, 0], [self._data.shape[1], n_dimensions])
# PCA
pca = tf.matmul(self._u, sigma)
with tf.Session(graph=self._graph) as session:
return session.run(pca, feed_dict={self._X: self._data})
```
6. 我們的`TF_PCA`類已準備就緒。 現在,我們將使用它來將 MNIST 數據從尺寸為 784(`28 x 28`)的每個輸入減少為尺寸為 3 的每個點的新數據。這里,我們僅保留了 10% 的信息以便于查看,但是通常需要保留大約 80% 的信息:
```py
tf_pca.fit()
pca = tf_pca.reduce(keep_info=0.1) # The reduced dimensions dependent upon the % of information
print('original data shape', mnist.train.images.shape)
print('reduced data shape', pca.shape)
```
以下是以下代碼的輸出:

7. 現在,讓我們在三維空間中繪制 55,000 個數據點:
```py
Set = sns.color_palette("Set2", 10)
color_mapping = {key:value for (key,value) in enumerate(Set)}
colors = list(map(lambda x: color_mapping[x], mnist.train.labels))
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(pca[:, 0], pca[:, 1],pca[:, 2], c=colors)
```
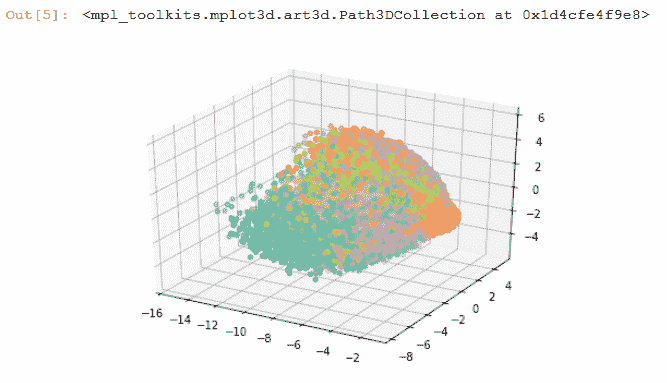
# 工作原理
前面的代碼對 MNIST 圖像執行降維。 每個原始圖像的尺寸為`28 x 28`; 使用 PCA 方法,我們可以將其減小到較小的尺寸。 通常,對于圖像數據,降維是必要的。 之所以如此,是因為圖像很大,并且包含大量的冗余數據。
# 更多
TensorFlow 提供了一種稱為**嵌入**的技術,該技術是將對象映射到向量中。 TensorBoard 的嵌入式投影儀允許我們以交互方式可視化模型中的嵌入。 嵌入式投影儀提供了三種降低尺寸的方法:PCA,t-SNE 和自定義。 我們可以使用 TensorBoard 的嵌入投影器實現與上一個類似的結果。 我們需要從`tensorflow.contrib.tensorboard.plugins`導入`projector`類,以從`tensorflow.contrib.tensorboard.plugins`導入`projector`進行相同的操作。 我們可以通過三個簡單的步驟來做到這一點:
1. 加載要探索其嵌入的數據:
```py
mnist = input_data.read_data_sets('MNIST_data')
images = tf.Variable(mnist.test.images, name='images')
```
2. 創建一個`metadata`文件((`metadata`文件是制表符分隔的`.tsv`文件):
```py
with open(metadata, 'w') as metadata_file:
for row in mnist.test.labels:
metadata_file.write('%d\n' % row)
```
3. 將嵌入內容保存在所需的`Log_DIR`中:
```py
with tf.Session() as sess:
saver = tf.train.Saver([images])
sess.run(images.initializer)
saver.save(sess, os.path.join(LOG_DIR, 'images.ckpt'))
config = projector.ProjectorConfig()
# One can add multiple embeddings.
embedding = config.embeddings.add()
embedding.tensor_name = images.name
# Link this tensor to its metadata file (e.g. labels).
embedding.metadata_path = metadata
# Saves a config file that TensorBoard will read during startup.
projector.visualize_embeddings(tf.summary.FileWriter(LOG_DIR), config)
```
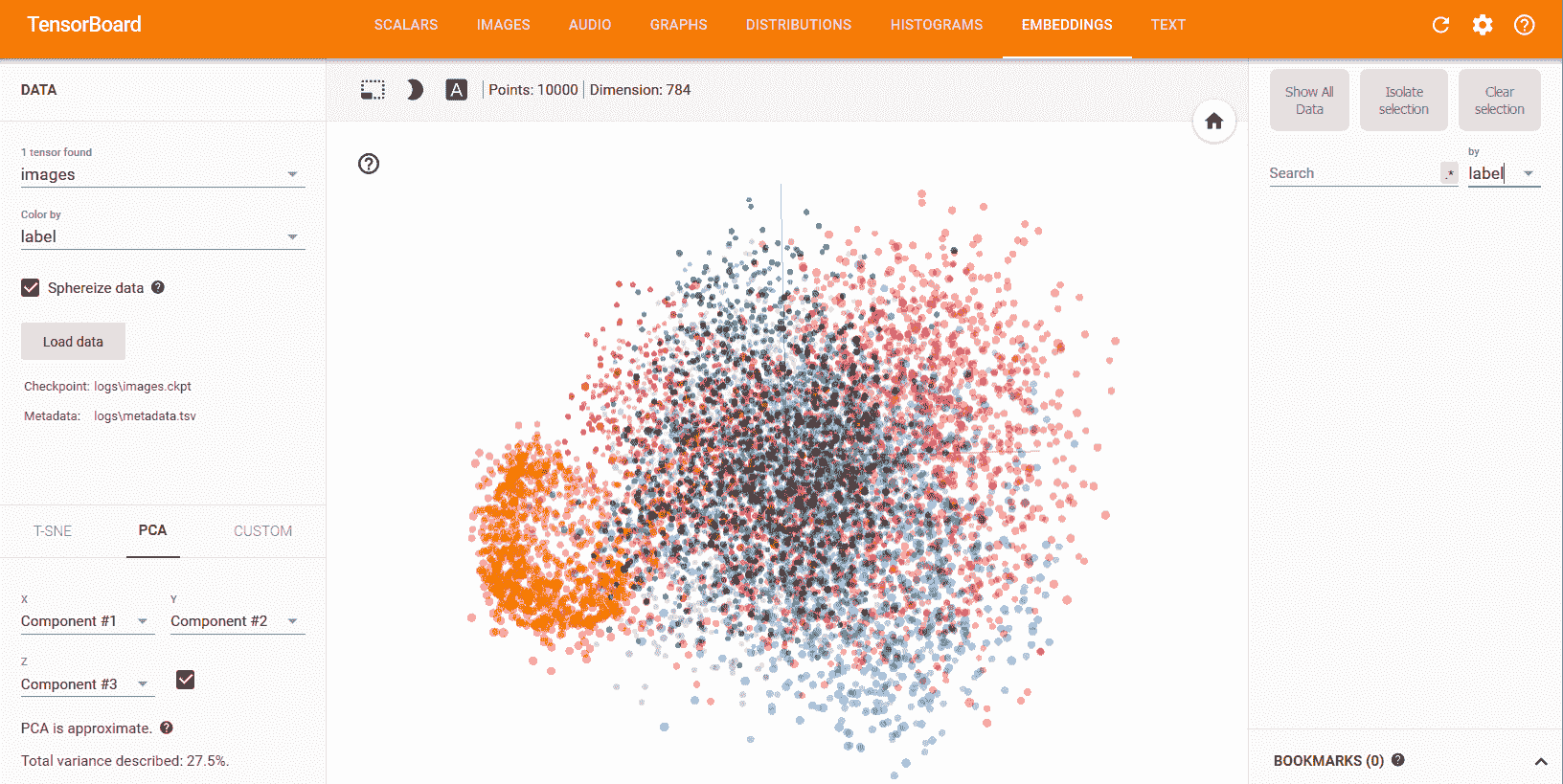
嵌入已準備就緒,現在可以使用 TensorBoard 看到。 通過 CLI `tensorboard --logdir=log`啟動 TensorBoard,在 Web 瀏覽器中打開 TensorBoard,然后轉到`EMBEDDINGS`選項卡。 這是使用 PCA 的 TensorBoard 投影,前三個主要成分為軸:
# 另見
* <https://arxiv.org/abs/1404.1100>
* <http://www.cs.otago.ac.nz/cosc453/student_tutorials/principal_components.pdf>
* <http://mplab.ucsd.edu/tutorials/pca.pdf>
* <http://projector.tensorflow.org/>
# K 均值聚類
顧名思義,K 均值聚類是一種對數據進行聚類的技術,即將數據劃分為指定數量的數據點。 這是一種無監督的學習技術。 它通過識別給定數據中的模式來工作。 還記得哈利波特成名的分揀帽子嗎? 書中的工作是聚類-將新生(未標記)的學生分成四個不同的類:格蘭芬多,拉文克勞,赫奇帕奇和斯萊特林。
人類非常擅長將對象分組在一起。 聚類算法試圖為計算機提供類似的功能。 有許多可用的聚類技術,例如“層次”,“貝葉斯”或“局部”。 K 均值聚類屬于部分聚類; 它將數據劃分為`k`簇。 每個簇都有一個中心,稱為**重心**。 簇數`k`必須由用戶指定。
K 均值算法以以下方式工作:
1. 隨機選擇`k`個數據點作為初始質心(集群中心)
2. 將每個數據點分配給最接近的質心; 可以找到接近度的不同方法,最常見的是歐幾里得距離
3. 使用當前簇成員資格重新計算質心,以使平方和的距離減小
4. 重復最后兩個步驟,直到達到收斂
# 準備
我們將使用 TensorFlow `KmeansClustering`估計器類來實現 K 均值。 它在[這個鏈接](https://github.com/tensorflow/tensorflow/blob/r1.3/tensorflow/contrib/learn/python/learn/estimators/kmeans.py)中定義。它創建一個模型來運行 K 均值和推理。 根據 TensorFlow 文檔,一旦創建了`KmeansClustering`類對象,就可以使用以下`__init__`方法實例化該對象:
```py
__init__(
num_clusters,
model_dir=None,
initial_clusters=RANDOM_INIT,
distance_metric=SQUARED_EUCLIDEAN_DISTANCE,
random_seed=0,
use_mini_batch=True,
mini_batch_steps_per_iteration=1,
kmeans_plus_plus_num_retries=2,
relative_tolerance=None,
config=None
)
```
TensorFlow 文檔對這些參數的定義如下:
**Args:**
**num_clusters**: The number of clusters to train.
**model_dir:** The directory to save the model results and log files.
**initial_clusters:** Specifies how to initialize the clusters for training. See clustering_ops.kmeans for the possible values.
**distance_metric:** The distance metric used for clustering. See clustering_ops.kmeans for the possible values.
**random_seed**: Python integer. Seed for PRNG used to initialize centers.
**use_mini_batch**: If true, use the mini-batch k-means algorithm. Or else assume full batch.
**mini_batch_steps_per_iteration**: The number of steps after which the updated cluster centers are synced back to a master copy. See clustering_ops.py for more details.
**kmeans_plus_plus_num_retries:** For each point that is sampled during kmeans++ initialization, this parameter specifies the number of additional points to draw from the current distribution before selecting the best. If a negative value is specified, a heuristic is used to sample O(log(num_to_sample)) additional points.
**relative_tolerance**: A relative tolerance of change in the loss between iterations. Stops learning if the loss changes less than this amount. Note that this may not work correctly if use_mini_batch=True.
**config**: See Estimator.
TensorFlow 支持歐幾里得距離和余弦距離作為質心的量度。 TensorFlow `KmeansClustering`提供了各種與`KmeansClustering`對象進行交互的方法。 在本秘籍中,我們將使用`fit()`,`clusters()`和`predict_clusters_idx()`方法:
```py
fit(
x=None,
y=None,
input_fn=None,
steps=None,
batch_size=None,
monitors=None,
max_steps=None
)
```
根據 TensorFlow 文檔,對于`KmeansClustering`估計器,我們需要向`fit()`提供`input_fn()`。 `cluster`方法返回聚類中心,`predict_cluster_idx`方法返回預測的聚類索引。
# 操作步驟
這是我們進行秘籍的方法:
1. 和以前一樣,我們從加載必要的模塊開始。 我們將像往常一樣需要 TensorFlow,NumPy 和 Matplotlib。 在本秘籍中,我們使用的是鳶尾花數據集,該數據集包含三個類別,每個類別有 50 個實例,其中每個類別都代表一種鳶尾花植物。 我們可以從[這里](https://archive.ics.uci.edu/ml/datasets/iris)下載數據作為`.csv`文件,也可以使用 sklearn 的數據集模塊(scikit-learn) 做任務:
```py
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
# dataset Iris
from sklearn import datasets
%matplotlib inline
```
2. 我們加載數據集:
```py
# import some data to play with
iris = datasets.load_iris()
x = iris.data[:, :2] # we only take the first two features.
y = iris.target
```
3. 讓我們看看該數據集的外觀:
```py
# original data without clustering
plt.scatter(hw_frame[:,0], hw_frame[:,1])
plt.xlabel('Sepia Length')
plt.ylabel('Sepia Width')
```
以下是以下代碼的輸出:
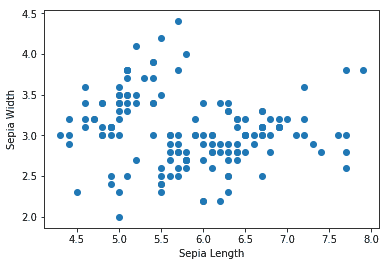
4. 我們可以看到在數據中沒有明顯可見的聚類。 現在我們定義`input_fn`,它將用于提供`fit`方法。 我們的輸入函數返回一個 TensorFlow 常數,該常數被分配了`x`的值和形狀,并且類型為`float`:
```py
def input_fn():
return tf.constant(np.array(x), tf.float32, x.shape),None
```
5. 現在我們使用`KmeansClustering`類; 在這里,我們已經知道類的數量為 3,因此我們將`num_clusters=3`設置為。 通常,我們不知道集群的數量。 在這種情況下,常用的方法是**肘部法則**:
```py
kmeans = tf.contrib.learn.KMeansClustering(num_clusters=3, relative_tolerance=0.0001, random_seed=2)
kmeans.fit(input_fn=input_fn)
```
6. 我們使用`clusters()`方法找到聚類,并使用`predict_cluster_idx()`方法為每個輸入點分配聚類索引:
```py
clusters = kmeans.clusters()
assignments = list(kmeans.predict_cluster_idex(input_fn=input_fn))
```
7. 現在讓我們可視化由 K 均值創建的聚類。 為此,我們創建一個包裝器函數`ScatterPlot`,該函數將`X`和`Y`值以及每個數據點的簇和簇索引一起使用:
```py
def ScatterPlot(X, Y, assignments=None, centers=None):
if assignments is None:
assignments = [0] * len(X)
fig = plt.figure(figsize=(14,8))
cmap = ListedColormap(['red', 'green', 'blue'])
plt.scatter(X, Y, c=assignments, cmap=cmap)
if centers is not None:
plt.scatter(centers[:, 0], centers[:, 1], c=range(len(centers)),
marker='+', s=400, cmap=cmap)
plt.xlabel('Sepia Length')
plt.ylabel('Sepia Width')
```
我們用它來繪制我們的`clusters`:
```py
ScatterPlot(x[:,0], x[:,1], assignments, clusters)
```
情節如下:
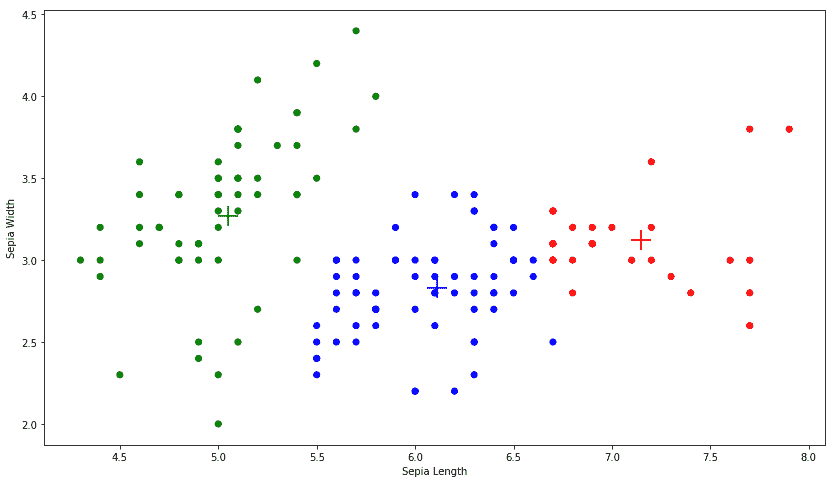
`+`標記是三個簇的質心。
# 工作原理
前面的秘籍使用 TensorFlow 的 K 均值聚類估計器將給定數據聚類為聚類。 在這里,由于我們知道集群的數量,我們決定保留`num_clusters=3`,但是在大多數情況下,如果使用未標記的數據,則永遠無法確定存在多少集群。 可以使用彎頭法確定最佳簇數。 該方法基于以下原則:我們應選擇能減少**平方誤差和**(**SSE**)距離的簇數。 如果`k`是簇數,則隨著`k`增加,SSE 減少,`SSE = 0`; 當`k`等于數據點數時,每個點都是其自己的簇。 我們想要一個`k`較低的值,以使 SSE 也較低。 在 TensorFlow 中,我們可以使用`KmeansClustering`類中定義的`score()`方法找到 SSE; 該方法將距離的總和返回到最近的聚類:
```py
sum_distances = kmeans.score(input_fn=input_fn, steps=100)
```
對于鳶尾數據,如果我們針對不同的`k`值繪制 SSE,則可以看到對于`k = 3`而言,SSE 的方差最高; 之后,它開始減小,因此肘點為`k = 3`:
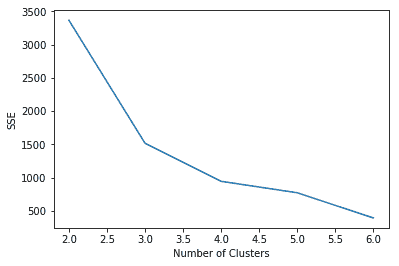
# 更多
K 均值聚類非常流行,因為它快速,簡單且健壯。 它還有一些缺點:最大的缺點是用戶必須指定簇的數量。 其次,該算法不能保證全局最優。 第三,它對異常值非常敏感。
# 另見
* `Kanungo, Tapas, et al. An efficient k-means clustering algorithm: Analysis and implementation. IEEE transactions on pattern analysis and machine intelligence 24.7 (2002): 881-892.`
* `Ortega, Joaquín Pérez, et al. Research issues on k-means algorithm: An experimental trial using matlab. CEUR Workshop Proceedings: Semantic Web and New Technologies.`
* <http://home.deib.polimi.it/matteucc/Clustering/tutorial_html/kmeans.html>
* `Chen, Ke. On coresets for k-median and k-means clustering in metric and euclidean spaces and their applications. SIAM Journal on Computing 39.3 (2009): 923-947.`
* <https://en.wikipedia.org/wiki/Determining_the_number_of_clusters_in_a_data_set>
# 自組織圖
**自組織映射**(**SOM**),有時也稱為 **Kohonen 網絡**或**勝者通吃單元**(**WTU**),是一種非常特殊的神經網絡,受人腦的獨特特征驅動。 在我們的大腦中,不同的感覺輸入以拓撲有序的方式表示。 與其他神經網絡不同,神經元并非都通過權重相互連接,而是會影響彼此的學習。 SOM 的最重要方面是神經元以拓撲方式表示學習的輸入。
在 SOM 中,神經元通常放置在(1D 或 2D)晶格的節點上。 更大的尺寸也是可能的,但實際上很少使用。 晶格中的每個神經元都通過權重矩陣連接到所有輸入單元。 在這里,您可以看到一個具有`3 x 4`(12 個神經元)和七個輸入的 SOM。 為了清楚起見,僅顯示將所有輸入連接到一個神經元的權重向量。 在這種情況下,每個神經元將具有七個元素,從而形成大小為(`12 x 7`)的組合權重矩陣:
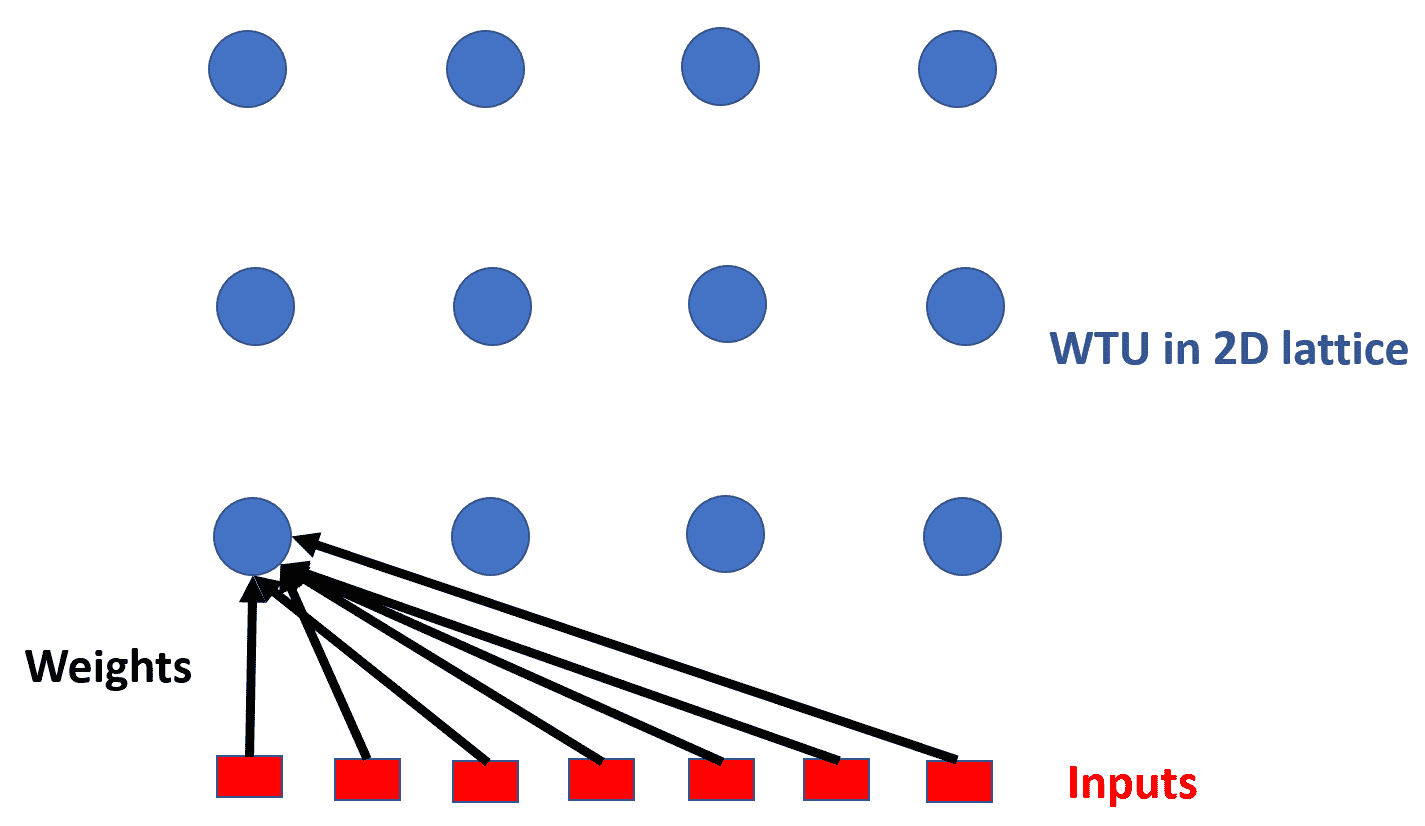
SOM 通過競爭性學習來學習。 可以將其視為 PCA 的非線性概括,因此,像 PCA 一樣,可以用于降維。
# 準備
為了實現 SOM,讓我們首先了解它是如何工作的。 第一步,將網絡的權重初始化為某個隨機值,或者通過從輸入中獲取隨機樣本進行初始化。 占據晶格中空間的每個神經元將被分配特定的位置。 現在,作為輸入出現,與輸入距離最小的神經元被宣布為 Winner(WTU)。 這是通過測量所有神經元的權重向量(`W`)和輸入向量(`X`)之間的距離來完成的:
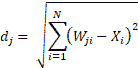
在此,`d[j]`是神經元`j`的權重與輸入`X`的距離。 最小`d`值的神經元是贏家。
接下來,以一種方式調整獲勝神經元及其相鄰神經元的權重,以確保如果下次出現相同的輸入,則相同的神經元將成為獲勝者。 為了確定哪些相鄰神經元需要修改,網絡使用鄰域函數`Λ(r)`; 通常,選擇高斯墨西哥帽函數作為鄰域函數。 鄰域函數在數學上表示如下:
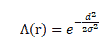
在這里,`σ`是神經元的時間依賴性半徑,`d`是其與獲勝神經元的距離:
鄰域函數的另一個重要屬性是其半徑隨時間減小。 結果,一開始,許多相鄰神經元的權重被修改,但是隨著網絡的學習,最終在學習過程中,一些神經元的權重(有時只有一個或沒有)被修改。 權重變化由以下公式給出:
`dW = η * Λ(X - W)`
我們繼續所有輸入的過程,并重復給定的迭代次數。 隨著迭代的進行,我們將學習率和半徑減小一個取決于迭代次數的因素。
# 操作步驟
我們按以下步驟進行:
1. 與往常一樣,我們從導入必要的模塊開始:
```py
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
2. 接下來,我們聲明一個類 WTU,它將執行所有任務。 用`m x n` 2D SOM 格的大小,`dim`輸入數據中的維數以及迭代總數來實例化該類:
```py
def __init__(self, m, n, dim, num_iterations, eta = 0.5, sigma = None):
"""
m x n : The dimension of 2D lattice in which neurons are arranged
dim : Dimension of input training data
num_iterations: Total number of training iterations
eta : Learning rate
sigma: The radius of neighbourhood function.
"""
self._m = m
self._n = n
self._neighbourhood = []
self._topography = []
self._num_iterations = int(num_iterations)
self._learned = False
```
3. 在`__init__`本身中,我們定義了計算圖和會話。
4. 如果網絡未提供任何`sigma`值,它將采用默認值,該值通常是 SOM 晶格最大尺寸的一半:
```py
if sigma is None:
sigma = max(m,n)/2.0 # Constant radius
else:
sigma = float(sigma)
```
5. 接下來,在圖中,我們聲明權重矩陣的變量,輸入的占位符以及計算獲勝者并更新其及其鄰居權重的計算步驟。 由于 SOM 提供了地形圖,因此我們還添加了操作以獲得神經元的地形位置:
```py
self._graph = tf.Graph()
# Build Computation Graph of SOM
with self._graph.as_default():
# Weight Matrix and the topography of neurons
self._W = tf.Variable(tf.random_normal([m*n, dim], seed = 0))
self._topography = tf.constant(np.array(list(self._neuron_location(m, n))))
# Placeholders for training data
self._X = tf.placeholder('float', [dim])
# Placeholder to keep track of number of iterations
self._iter = tf.placeholder('float')
# Finding the Winner and its location
d = tf.sqrt(tf.reduce_sum(tf.pow(self._W - tf.stack([self._X
for i in range(m*n)]),2),1))
self.WTU_idx = tf.argmin(d,0)
slice_start = tf.pad(tf.reshape(self.WTU_idx, [1]),np.array([[0,1]]))
self.WTU_loc = tf.reshape(tf.slice(self._topography, slice_start, [1,2]), [2])
# Change learning rate and radius as a function of iterations
learning_rate = 1 - self._iter/self._num_iterations
_eta_new = eta * learning_rate
_sigma_new = sigma * learning_rate
# Calculating Neighbourhood function
distance_square = tf.reduce_sum(tf.pow(tf.subtract(
self._topography, tf.stack([self.WTU_loc for i in range(m * n)])), 2), 1)
neighbourhood_func = tf.exp(tf.negative(tf.div(tf.cast(
distance_square, "float32"), tf.pow(_sigma_new, 2))))
# multiply learning rate with neighbourhood func
eta_into_Gamma = tf.multiply(_eta_new, neighbourhood_func)
# Shape it so that it can be multiplied to calculate dW
weight_multiplier = tf.stack([tf.tile(tf.slice(
eta_into_Gamma, np.array([i]), np.array([1])), [dim])
for i in range(m * n)])
delta_W = tf.multiply(weight_multiplier,
tf.subtract(tf.stack([self._X for i in range(m * n)]),self._W))
new_W = self._W + delta_W
self._training = tf.assign(self._W,new_W)
# Initialize All variables
init = tf.global_variables_initializer()
self._sess = tf.Session()
self._sess.run(init)
```
6. 我們為該類定義一個`fit`方法,該方法執行在該類的默認圖中聲明的訓練操作。 該方法還計算質心網格:
```py
def fit(self, X):
"""
Function to carry out training
"""
for i in range(self._num_iterations):
for x in X:
self._sess.run(self._training, feed_dict= {self._X:x, self._iter: i})
# Store a centroid grid for easy retreival
centroid_grid = [[] for i in range(self._m)]
self._Wts = list(self._sess.run(self._W))
self._locations = list(self._sess.run(self._topography))
for i, loc in enumerate(self._locations):
centroid_grid[loc[0]].append(self._Wts[i])
self._centroid_grid = centroid_grid
self._learned = True
```
7. 我們定義一個函數來確定獲勝神經元在 2D 晶格中的索引和位置:
```py
def winner(self, x):
idx = self._sess.run([self.WTU_idx,self.WTU_loc], feed_dict = {self._X:x})
return idx
```
8. 我們定義一些更多的輔助函數,以執行晶格中神經元的 2D 映射并將輸入向量映射到 2D 晶格中的相關神經元:
```py
def _neuron_location(self,m,n):
"""
Function to generate the 2D lattice of neurons
"""
for i in range(m):
for j in range(n):
yield np.array([i,j])
def get_centroids(self):
"""
Function to return a list of 'm' lists, with each inner list containing the 'n' corresponding centroid locations as 1-D NumPy arrays.
"""
if not self._learned:
raise ValueError("SOM not trained yet")
return self._centroid_grid
```
```py
def map_vects(self, X):
"""
Function to map each input vector to the relevant neuron in the lattice
"""
if not self._learned:
raise ValueError("SOM not trained yet")
to_return = []
for vect in X:
min_index = min([i for i in range(len(self._Wts))],
key=lambda x: np.linalg.norm(vect -
self._Wts[x]))
to_return.append(self._locations[min_index])
return to_return
```
9. 現在我們的 WTU 類已經準備好,我們從`.csv`文件中讀取數據并對其進行規范化:
```py
def normalize(df):
result = df.copy()
for feature_name in df.columns:
max_value = df[feature_name].max()
min_value = df[feature_name].min()
result[feature_name] = (df[feature_name] - min_value) / (max_value - min_value)
return result
# Reading input data from file
import pandas as pd
df = pd.read_csv('colors.csv') # The last column of data file is a label
data = normalize(df[['R', 'G', 'B']]).values
name = df['Color-Name'].values
n_dim = len(df.columns) - 1
# Data for Training
colors = data
color_names = name
```
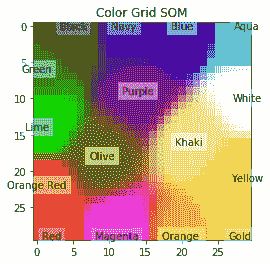
10. 最后,我們使用我們的類執行降維并將其布置在美麗的地形圖中:
```py
som = WTU(30, 30, n_dim, 400, sigma=10.0)
som.fit(colors)
# Get output grid
image_grid = som.get_centroids()
# Map colours to their closest neurons
mapped = som.map_vects(colors)
# Plot
plt.imshow(image_grid)
plt.title('Color Grid SOM')
for i, m in enumerate(mapped):
plt.text(m[1], m[0], color_names[i], ha='center', va='center', bbox=dict(facecolor='white', alpha=0.5, lw=0))
```
情節如下:
# 工作原理
SOM 在計算上很昂貴,因此對于非常大的數據集并沒有真正的用處。 盡管如此,它們仍然易于理解,并且可以很好地找到輸入數據之間的相似性。 因此,它們已被用于圖像分割和確定 NLP 中的單詞相似度圖。
# 另見
* [這是一篇非常不錯的博客文章,用簡單的語言解釋了 SOM](http://www.ai-junkie.com/ann/som/som1.html)
* [關于 SOM 的簡要介紹](https://en.wikipedia.org/wiki/Self-organizing_map)
* [Kohonen 關于 SOM 的開創性論文:“自組織圖”。 神經計算 21.1(1998):1-6](https://pdfs.semanticscholar.org/8c6a/aea3159e9f49283de252d0548b337839ca6f.pdf)
# 受限玻爾茲曼機
**受限玻爾茲曼機**(**RBM**)是兩層神經網絡,第一層稱為**可見層**,第二層稱為隱藏層。 它們被稱為**淺層神經網絡**,因為它們只有兩層深。 它們最初是由 1986 年由保羅·斯莫倫斯基(Paul Smolensky)提出的(他稱其為 Harmony Networks),后來由 Geoffrey Hinton 提出,于 2006 年提出了**對比發散**(**CD**)作為訓練他們的方法。 可見層中的所有神經元都與隱藏層中的所有神經元相連,但是存在**限制**-同一層中沒有神經元可以連接。 所有神經元本質上都是二進制的:
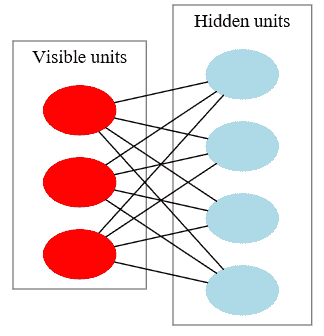
[資料來源:Qwertyus 自己的作品,CC BY-SA 3.0](https://commons.wikimedia.org/w/index.php?curid=22717044)
RBM 可用于降維,特征提取和協作過濾。 RBM 中的訓練可分為三個部分:前進,后退和比較。
# 準備
讓我們看看制作 RBM 所需的表達式:
**正向傳遞**:可見單元(`V`)上的信息通過權重(`W`)和偏差(`c`)傳遞給隱藏的對象單元(`h[0]`)。 隱藏單元是否可以觸發取決于隨機概率(`σ`是隨機概率):
`p(h[i]|v[0]) = σ(V^T · W + c)[i]`
**向后傳遞**:隱藏的單元表示(`h[0]`)然后通過相同的權重`W`但不同的偏置`c`傳遞回可見單元,它們在其中重構輸入。 再次,對輸入進行采樣:
`p(v[i]|h[0]) = σ(W^T · h[0] + b)[i]`*
將這兩個遍重復 k 步或直到達到收斂。 根據研究人員的說法,`k = 1`給出了很好的結果,因此我們將保持`k = 1`。
可見向量`V`和隱藏向量的聯合構型具有如下能量:
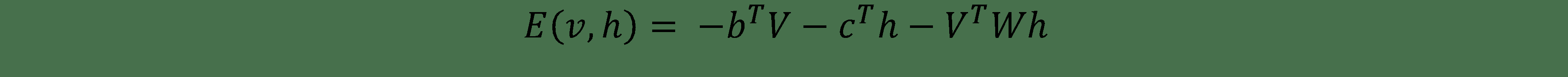
自由能還與每個可見向量`V`相關,為與具有`V`的所有構型具有相同概率的單個配置所需的能量:

使用對比度發散目標函數,即`Mean(F(Voriginal))- Mean(F(Vreconstructed))`,權重的變化由此給出:
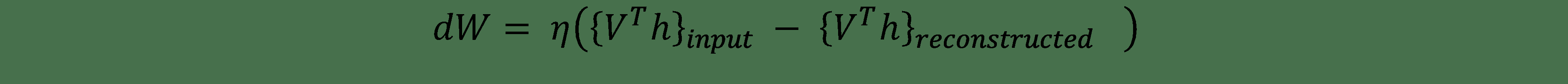
在此,`η`是學習率。 對于偏差`b`和`c`存在相似的表達式。
# 操作步驟
我們按以下步驟進行:
1. 導入模塊:
```py
import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt
%matplotlib inline
```
2. 聲明 RBM 類,它將完成主要任務。 `__init__`將建立完整的圖,正向和反向傳遞以及目標函數; 我們將使用 TensorFlow 內置的優化器來更新權重和偏差:
```py
class RBM(object):
def __init__(self, m, n):
"""
m: Number of neurons in visible layer
n: number of neurons in hidden layer
"""
self._m = m
self._n = n
# Create the Computational graph
# Weights and biases
self._W = tf.Variable(tf.random_normal(shape=(self._m,self._n)))
self._c = tf.Variable(np.zeros(self._n).astype(np.float32)) #bias for hidden layer
self._b = tf.Variable(np.zeros(self._m).astype(np.float32)) #bias for Visible layer
# Placeholder for inputs
self._X = tf.placeholder('float', [None, self._m])
# Forward Pass
_h = tf.nn.sigmoid(tf.matmul(self._X, self._W) + self._c)
self.h = tf.nn.relu(tf.sign(_h - tf.random_uniform(tf.shape(_h))))
#Backward pass
_v = tf.nn.sigmoid(tf.matmul(self.h, tf.transpose(self._W)) + self._b)
self.V = tf.nn.relu(tf.sign(_v - tf.random_uniform(tf.shape(_v))))
# Objective Function
objective = tf.reduce_mean(self.free_energy(self._X)) - tf.reduce_mean(
self.free_energy(self.V))
self._train_op = tf.train.GradientDescentOptimizer(1e-3).minimize(objective)
# Cross entropy cost
reconstructed_input = self.one_pass(self._X)
self.cost = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(
labels=self._X, logits=reconstructed_input))
```
3. 我們在`RBM`類中定義`fit()`方法。 在`__init__`中聲明了所有操作后,訓練只是在會話中調用`train_op`。 我們使用批量訓練:
```py
def fit(self, X, epochs = 1, batch_size = 100):
N, D = X.shape
num_batches = N // batch_size
obj = []
for i in range(epochs):
#X = shuffle(X)
for j in range(num_batches):
batch = X[j * batch_size: (j * batch_size + batch_size)]
_, ob = self.session.run([self._train_op,self.cost ], feed_dict={self._X: batch})
if j % 10 == 0:
print('training epoch {0} cost {1}'.format(j,ob))
obj.append(ob)
return obj
```
4. 還有其他輔助函數可計算對率誤差并從網絡返回重建的圖像:
```py
def set_session(self, session):
self.session = session
def free_energy(self, V):
b = tf.reshape(self._b, (self._m, 1))
term_1 = -tf.matmul(V,b)
term_1 = tf.reshape(term_1, (-1,))
term_2 = -tf.reduce_sum(tf.nn.softplus(tf.matmul(V,self._W) +
self._c))
return term_1 + term_2
def one_pass(self, X):
h = tf.nn.sigmoid(tf.matmul(X, self._W) + self._c)
return tf.matmul(h, tf.transpose(self._W)) + self._b
def reconstruct(self,X):
x = tf.nn.sigmoid(self.one_pass(X))
return self.session.run(x, feed_dict={self._X: X})
```
5. 我們加載 MNIST 數據集:
```py
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
trX, trY, teX, teY = mnist.train.images, mnist.train.labels, mnist.test.images, mnist.test.labels
```
6. 接下來,我們在 MNIST 數據集上訓練`RBM`:
```py
Xtrain = trX.astype(np.float32)
Xtest = teX.astype(np.float32)
_, m = Xtrain.shape
rbm = RBM(m, 100)
#Initialize all variables
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
rbm.set_session(sess)
err = rbm.fit(Xtrain)
out = rbm.reconstruct(Xest[0:100]) # Let us reconstruct Test Data
```
7. 不同**周期**的函數誤差:
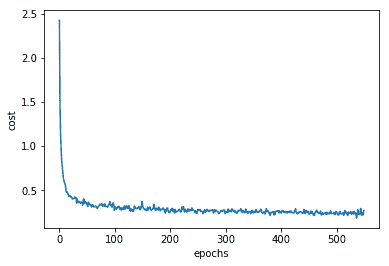
# 工作原理
由于其具有重建圖像的能力,RBM 可用于從現有數據中生成更多數據。 通過制作一個小的助手繪圖代碼,我們可以看到原始和重建的 MNIST 圖像:
```py
row, col = 2, 8
idx = np.random.randint(0, 100, row * col // 2)
f, axarr = plt.subplots(row, col, sharex=True, sharey=True, figsize=(20,4))
for fig, row in zip([Xtest_noisy,out], axarr):
for i,ax in zip(idx,row):
ax.imshow(fig[i].reshape((28, 28)), cmap='Greys_r')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
```
我們得到的結果如下:

# 另見
* `Smolensky, Paul. Information processing in dynamical systems: Foundations of harmony theory. No. CU-CS-321-86. COLORADO UNIV AT BOULDER DEPT OF COMPUTER SCIENCE, 1986.`
<http://stanford.edu/~jlmcc/papers/PDP/Volume%201/Chap6_PDP86.pdf>
* `Salakhutdinov, Ruslan, Andriy Mnih, and Geoffrey Hinton. Restricted Boltzmann machines for collaborative filtering. Proceedings of the 24th international conference on Machine learning. ACM, 2007.`
<http://machinelearning.wustl.edu/mlpapers/paper_files/icml2007_SalakhutdinovMH07.pdf>
* `Hinton, Geoffrey. A practical guide to training restricted Boltzmann machines. Momentum 9.1 (2010): 926.`
<http://www.csri.utoronto.ca/~hinton/absps/guideTR.pdf)>
* 如果您對數學感興趣,[這是一個很好的教程](http://deeplearning.net/tutorial/rbm.html#rbm)
# 使用 RBM 的推薦系統
網上零售商廣泛使用推薦系統向客戶推薦產品。 例如,亞馬遜會告訴您購買此商品的其他客戶對什么感興趣,或者 Netflix 根據您所觀看的內容以及有相同興趣的其他 Netflix 用戶所觀看的內容推薦電視連續劇和電影。 這些推薦器系統在協作篩選的基礎上工作。 在協作過濾中,系統根據用戶的過去行為來構建模型。 我們將使用上一個秘籍中的 RBM 構建一個使用協作過濾來推薦電影的推薦器系統。 這項工作中的一個重要挑戰是,大多數用戶不會對所有產品/電影進行評分,因此大多數數據都將丟失。 如果有 M 個產品和 N 個用戶,則我們需要構建一個數組`N x M`,其中包含用戶的已知等級并將所有未知值設為零。
# 準備
為了使用協作過濾創建推薦系統,我們需要修改數據。 作為說明,我們將使用來自[這里](https://grouplens.org/datasets/movielens/)的電影數據集。 數據由兩個`.dat`文件組成:`movies.dat`和`ratings.dat`。 `movies.dat`文件包含 3 列:3883 個電影的 MovieID,Title 和 Genre。 `ratings.dat`文件包含四列:UserID,MovieID,Rating 和 Time。 我們需要合并這兩個數據文件,以便能夠構建一個數組,其中對于每個用戶,我們對所有 3,883 部電影都有一個評分。 問題在于用戶通常不會對所有電影進行評級,因此我們僅對某些電影進行非零(標準化)評級。 其余部分設為零,因此不會對隱藏層有所貢獻。
# 操作步驟
1. 我們將使用在先前秘籍中創建的`RBM`類。 讓我們定義我們的 RBM 網絡; 可見單元的數量將是電影的數量,在我們的示例中為 3883(`movies_df`是包含`movies.dat`文件中的數據的數據幀):
```py
m = len(movies_df) # Number of visible units
n = 20 # Number of Hidden units
recommender = rbm.RBM(m,n)
```
2. 我們使用 Pandas 合并和`groupby`命令創建了一個列表`trX`,該列表包含大約 1,000 個用戶的規范化電影評分。 列表的大小為`1000 x 3883`。我們使用它來訓練我們的 RBM:
```py
Xtrain = np.array(trX)
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
recommender.set_session(sess)
err = recommender.fit(Xtrain, epochs=10)
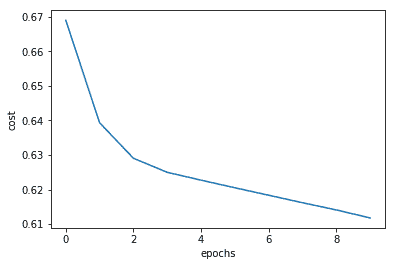
```
3. 每個周期的跨邏輯誤差減少:
4. 網絡現已接受訓練; 我們使用它為索引為 150 的隨機用戶(可能是任何現有用戶)獲得推薦:
```py
user_index = 150
x = np.array([Xtrain[user_index, :]])
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
recommender.set_session(sess)
out = recommender.reconstruct(x.astype(np.float32))
```
5. 結果與現有數據幀合并,我們可以看到該用戶的推薦分數:
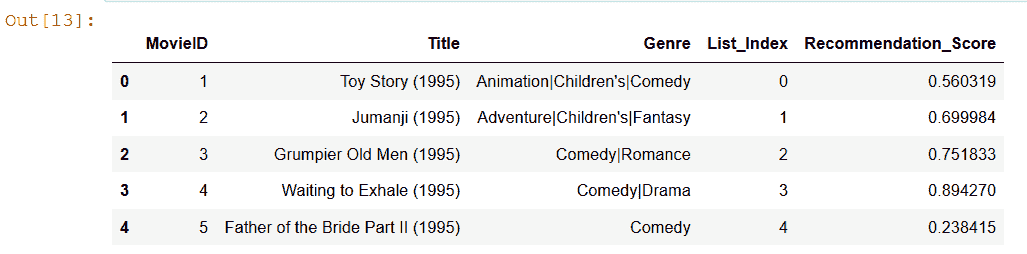
# 更多
杰弗里·欣頓(Geoffrey Hinton)教授領導的多倫多大學團隊贏得了 Netflix 最佳協作過濾競賽的冠軍,該協作過濾使用 [RBM](https://en.wikipedia.org/wiki/Netflix_Prize) 來預測電影的用戶收視率。 [可以從他們的論文中獲取其工作的詳細信息](http://www.cs.toronto.edu/~hinton/absps/netflixICML.pdf)。
一個 RBM 的隱藏單元的輸出可以饋送到另一個 RBM 的可見單元,可以重復此過程以形成 RBM 的棧。 這導致**棧式 RBM** 。 假定不存在其他堆疊式 RBM,則對其進行獨立訓練。 大量棧式 RBM 構成了**深度信念網絡(DBN)**。 可以使用有監督或無監督的訓練來訓練 DBN。 您將在下一個秘籍中了解有關它們的更多信息。
# 用于情感檢測的 DBN
在本秘籍中,我們將學習如何首先堆疊 RBM 來制作 DBN,然后訓練它來檢測情感。 秘籍中有趣的部分是我們采用了兩種不同的學習范例:首先,我們使用無監督學習對 RBM 進行了預訓練,最后,我們有了一個 MLP 層,該層是使用監督學習進行了訓練的。
# 準備
我們使用已經在秘籍*受限玻爾茲曼機*中創建的 RBM 類,只需進行一次更改即可,現在無需在訓練后重建圖像。 取而代之的是,我們棧式 RBM 將僅將數據轉發至 DBN 的最后一個 MLP 層。 這是通過從類中刪除`reconstruct()`函數并將其替換為`rbm_output()`函數來實現的:
```py
def rbm_output(self,X):
x = tf.nn.sigmoid(tf.matmul(X, self._W) + self._c)
return self.session.run(x, feed_dict={self._X: X})
```
對于數據,我們考慮了 Kaggle 面部表情識別數據,該數據可從[這里](https://www.kaggle.com/c/challenges-in-representation-learning-facial-expression-recognition-challenge)獲得。 此處給出的數據描述為:
數據由`48 x 48`像素的面部灰度圖像組成。 面部已自動注冊,因此面部或多或少居中,并且在每個圖像中占據大約相同的空間量。 任務是根據面部表情中顯示的情感將每個面孔分類為七個類別之一(0 為憤怒,1 惡心,2 為恐懼,3 為快樂,4 為悲傷,5 為驚奇,6 為中性) 。
`train.csv`包含兩列,“情感”和“像素”。 “情感”列包含圖像中存在的情感的數字代碼,范圍從 0 到 6(含)。 “像素”列包含每個圖像用引號引起來的字符串。 該字符串的內容是按行主要順序分隔的像素值。 `test.csv`僅包含“像素”列,您的任務是預測情感列。
訓練集包含 28,709 個示例。 用于排行榜的公共測試集包含 3,589 個示例。 最終測試集用于確定比賽的獲勝者,另外還有 3,589 個示例。
該數據集由 Pierre-Luc Carrier 和 Aaron Courville 進行,是正在進行的研究項目的一部分。 他們為研討會的組織者提供了他們數據集的初步版本,供比賽使用。
完整的數據合而為一。 名為`fer2013.csv`的`csv`文件。 我們從中分離出訓練,驗證和測試數據:
```py
data = pd.read_csv('data/fer2013.csv')
tr_data = data[data.Usage == "Training"]
test_data = data[data.Usage == "PublicTest"]
mask = np.random.rand(len(tr_data)) < 0.8
train_data = tr_data[mask]
val_data = tr_data[~mask]
```
我們將需要預處理數據,即將像素和情感標簽分開。 為此,我們制作了兩個函數`dense_to_one_hot ()`,它對標簽執行了單熱編碼。 第二個函數是`preprocess_data()`,它將單個像素分離為一個數組。 在這兩個函數的幫助下,我們生成了訓練,驗證和測試數據集的輸入特征和標簽:
```py
def dense_to_one_hot(labels_dense, num_classes):
num_labels = labels_dense.shape[0]
index_offset = np.arange(num_labels) * num_classes
labels_one_hot = np.zeros((num_labels, num_classes))
labels_one_hot.flat[index_offset + labels_dense.ravel()] = 1
return labels_one_hot
def preprocess_data(dataframe):
pixels_values = dataframe.pixels.str.split(" ").tolist()
pixels_values = pd.DataFrame(pixels_values, dtype=int)
images = pixels_values.values
images = images.astype(np.float32)
images = np.multiply(images, 1.0/255.0)
labels_flat = dataframe["emotion"].values.ravel()
labels_count = np.unique(labels_flat).shape[0]
labels = dense_to_one_hot(labels_flat, labels_count)
labels = labels.astype(np.uint8)
return images, labels
```
使用前面代碼中定義的函數,我們以訓練所需的格式獲取數據。 基于本文針對 MNIST 提到的相似原理,我們構建了[情感檢測 DBN](https://www.cs.toronto.edu/~hinton/absps/fastnc.pdf)。
# 操作步驟
我們按以下步驟進行:
1. 我們需要導入標準模塊 TensorFlow,NumPy 和 Pandas,以讀取`.csv`文件和 Matplolib:
```py
import tensorflow as tf
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
```
2. 訓練,驗證和測試數據是使用輔助函數獲得的:
```py
X_train, Y_train = preprocess_data(train_data)
X_val, Y_val = preprocess_data(val_data)
X_test, Y_test = preprocess_data(test_data)
```
3. 讓我們來探討一下我們的數據。 我們繪制平均圖像并找到每個訓練,驗證和測試數據集中的圖像數量:
```py
# Explore Data
mean_image = X_train.mean(axis=0)
std_image = np.std(X_train, axis=0)
print("Training Data set has {} images".format(len(X_train)))
print("Validation Data set has {} images".format(len(X_val)))
print("Test Data set has {} images".format(len(X_test)))
plt.imshow(mean_image.reshape(48,48), cmap='gray')
```
我們得到的結果如下:
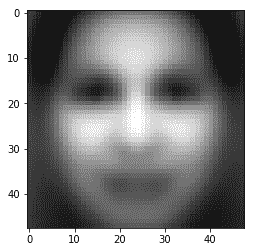
4. 我們還會看到訓練樣本中的圖像及其各自的標簽:
```py
classes = ['angry','disgust','fear','happy','sad','surprise','neutral']
num_classes = len(classes)
samples_per_class = 7
for y,cls in enumerate(classes):
idxs = np.flatnonzero(np.argmax(Y_train, axis =1) == y)
idxs = np.random.choice(idxs, samples_per_class, replace=False)
for i, idx in enumerate(idxs):
plt_idx = i * num_classes + y + 1
plt.subplot(samples_per_class, num_classes, plt_idx)
plt.imshow(X_train[idx].reshape(48,48), cmap='gray') #pixel height and width
plt.axis('off')
if i == 0:
plt.title(cls)
plt.show()
```
情節如下:

5. 接下來,我們定義 RBM 棧; 每個 RBM 都將先前 RBM 的輸出作為其輸入:
```py
RBM_hidden_sizes = [1500, 700, 400] #create 4 layers of RBM with size 1500, 700, 400 and 100
#Set input as training data
inpX = X_train
#Create list to hold our RBMs
rbm_list = []
#Size of inputs is the number of inputs in the training set
input_size = inpX.shape[1]
#For each RBM we want to generate
for i, size in enumerate(RBM_hidden_sizes):
print ('RBM: ',i,' ',input_size,'->', size)
rbm_list.append(RBM(input_size, size))
input_size = size
```
這將生成三個 RBM:第一個 RBM 具有 2304(`48×48`)個輸入和 1500 個隱藏單元,第二個 RBM 具有 1500 個輸入和 700 個隱藏單元,最后第三個 RBM 具有 700 個輸入和 400 個隱藏單元。
6. 我們逐一訓練每個 RBM。 該技術也稱為**貪婪訓練**。 在原始論文中,用于在 MNIST 上訓練每個 RBM 的周期數是 30,因此在這里,增加周期也應會改善網絡的表現:
```py
# Greedy wise training of RBMs
init = tf.global_variables_initializer()
for rbm in rbm_list:
print ('New RBM:')
#Train a new one
with tf.Session() as sess:
sess.run(init)
rbm.set_session(sess)
err = rbm.fit(inpX, 5)
inpX_n = rbm.rbm_output(inpX)
print(inpX_n.shape)
inpX = inpX_n
```
7. 我們定義一個`DBN`類。 在類中,我們用三層 RBM 和另外兩層 MLP 構建完整的 DBN。 從預訓練的 RBM 中加載 RBM 層的權重。 我們還聲明了訓練和預測 DBN 的方法; 為了進行微調,網絡嘗試最小化均方損失函數:
```py
class DBN(object):
def __init__(self, sizes, X, Y, eta = 0.001, momentum = 0.0, epochs = 10, batch_size = 100):
#Initialize hyperparameters
self._sizes = sizes
print(self._sizes)
self._sizes.append(1000) # size of the first FC layer
self._X = X
self._Y = Y
self.N = len(X)
self.w_list = []
self.c_list = []
self._learning_rate = eta
self._momentum = momentum
self._epochs = epochs
self._batchsize = batch_size
input_size = X.shape[1]
#initialization loop
for size in self._sizes + [Y.shape[1]]:
#Define upper limit for the uniform distribution range
max_range = 4 * math.sqrt(6\. / (input_size + size))
#Initialize weights through a random uniform distribution
self.w_list.append(
np.random.uniform( -max_range, max_range, [input_size, size]).astype(np.float32))
#Initialize bias as zeroes
self.c_list.append(np.zeros([size], np.float32))
input_size = size
# Build DBN
#Create placeholders for input, weights, biases, output
self._a = [None] * (len(self._sizes) + 2)
self._w = [None] * (len(self._sizes) + 1)
self._c = [None] * (len(self._sizes) + 1)
self._a[0] = tf.placeholder("float", [None, self._X.shape[1]])
self.y = tf.placeholder("float", [None, self._Y.shape[1]])
#Define variables and activation function
for i in range(len(self._sizes) + 1):
self._w[i] = tf.Variable(self.w_list[i])
self._c[i] = tf.Variable(self.c_list[i])
for i in range(1, len(self._sizes) + 2):
self._a[i] = tf.nn.sigmoid(tf.matmul(self._a[i - 1], self._w[i - 1]) + self._c[i - 1])
#Define the cost function
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=self.y, logits= self._a[-1]))
#cost = tf.reduce_mean(tf.square(self._a[-1] - self.y))
#Define the training operation (Momentum Optimizer minimizing the Cost function)
self.train_op = tf.train.AdamOptimizer(learning_rate=self._learning_rate).minimize(cost)
#Prediction operation
self.predict_op = tf.argmax(self._a[-1], 1)
#load data from rbm
def load_from_rbms(self, dbn_sizes,rbm_list):
#Check if expected sizes are correct
assert len(dbn_sizes) == len(self._sizes)
for i in range(len(self._sizes)):
#Check if for each RBN the expected sizes are correct
assert dbn_sizes[i] == self._sizes[i]
#If everything is correct, bring over the weights and biases
for i in range(len(self._sizes)-1):
self.w_list[i] = rbm_list[i]._W
self.c_list[i] = rbm_list[i]._c
def set_session(self, session):
self.session = session
#Training method
def train(self, val_x, val_y):
#For each epoch
num_batches = self.N // self._batchsize
batch_size = self._batchsize
for i in range(self._epochs):
#For each step
for j in range(num_batches):
batch = self._X[j * batch_size: (j * batch_size + batch_size)]
batch_label = self._Y[j * batch_size: (j * batch_size + batch_size)]
self.session.run(self.train_op, feed_dict={self._a[0]: batch, self.y: batch_label})
for j in range(len(self._sizes) + 1):
#Retrieve weights and biases
self.w_list[j] = sess.run(self._w[j])
self.c_list[j] = sess.run(self._c[j])
train_acc = np.mean(np.argmax(self._Y, axis=1) ==
self.session.run(self.predict_op, feed_dict={self._a[0]: self._X, self.y: self._Y}))
val_acc = np.mean(np.argmax(val_y, axis=1) ==
self.session.run(self.predict_op, feed_dict={self._a[0]: val_x, self.y: val_y}))
print (" epoch " + str(i) + "/" + str(self._epochs) + " Training Accuracy: " + str(train_acc) + " Validation Accuracy: " + str(val_acc))
def predict(self, X):
return self.session.run(self.predict_op, feed_dict={self._a[0]: X})
```
8. 現在,我們訓練實例化`DBN`對象并對其進行訓練。 并預測測試數據的標簽:
```py
nNet = DBN(RBM_hidden_sizes, X_train, Y_train, epochs = 80)
with tf.Session() as sess:
#Initialize Variables
sess.run(tf.global_variables_initializer())
nNet.set_session(sess)
nNet.load_from_rbms(RBM_hidden_sizes,rbm_list)
nNet.train(X_val, Y_val)
y_pred = nNet.predict(X_test)
```
# 工作原理
RBM 使用無監督學習來學習模型的隱藏表示/特征,然后對與預訓練 RBM 一起添加的全連接層進行微調。
這里的精度在很大程度上取決于圖像表示。 在前面的秘籍中,我們沒有使用圖像處理,僅使用了 0 到 1 之間縮放的灰度圖像。但是,如果我們按照以下論文所述添加圖像處理,[則會進一步提高精度](http://deeplearning.net/wp-content/uploads/2013/03/dlsvm.pdf)。 因此,我們在`preprocess_data`函數中將每個圖像乘以 100.0/255.0,然后將以下幾行代碼添加到主代碼中:
```py
std_image = np.std(X_train, axis=0)
X_train = np.divide(np.subtract(X_train,mean_image), std_image)
X_val = np.divide(np.subtract(X_val,mean_image), std_image)
X_test = np.divide(np.subtract(X_test,mean_image), std_image)
```
# 更多
在前面的示例中,沒有進行預處理,這三個數據集的準確率大約為 40%。 但是,當我們添加預處理時,訓練數據的準確率將提高到 90%,但是對于驗證和測試,我們仍然可以獲得約 45% 的準確率。
可以引入許多更改來改善結果。 首先,我們在秘籍中使用的數據集是只有 22,000 張圖像的 Kaggle 數據集。 如果觀察這些圖像,則會發現僅過濾面部的步驟會改善結果。 如下文所述,[另一種策略是增加隱藏層的大小而不是減小它們的大小](https://www.cs.swarthmore.edu/~meeden/cs81/s14/papers/KevinVincent.pdf)。
在識別情感方面確實非常成功的另一個更改是[使用面部關鍵點而不是整個面部訓練](http://cs229.stanford.edu/proj2010/McLaughlinLeBayanbat-RecognizingEmotionsWithDeepBeliefNets.pdf)。
使用前面的秘籍,您可以嘗試這些更改并探索表現如何提高。 愿 GPU 力量與您同在!
- TensorFlow 1.x 深度學習秘籍
- 零、前言
- 一、TensorFlow 簡介
- 二、回歸
- 三、神經網絡:感知器
- 四、卷積神經網絡
- 五、高級卷積神經網絡
- 六、循環神經網絡
- 七、無監督學習
- 八、自編碼器
- 九、強化學習
- 十、移動計算
- 十一、生成模型和 CapsNet
- 十二、分布式 TensorFlow 和云深度學習
- 十三、AutoML 和學習如何學習(元學習)
- 十四、TensorFlow 處理單元
- 使用 TensorFlow 構建機器學習項目中文版
- 一、探索和轉換數據
- 二、聚類
- 三、線性回歸
- 四、邏輯回歸
- 五、簡單的前饋神經網絡
- 六、卷積神經網絡
- 七、循環神經網絡和 LSTM
- 八、深度神經網絡
- 九、大規模運行模型 -- GPU 和服務
- 十、庫安裝和其他提示
- TensorFlow 深度學習中文第二版
- 一、人工神經網絡
- 二、TensorFlow v1.6 的新功能是什么?
- 三、實現前饋神經網絡
- 四、CNN 實戰
- 五、使用 TensorFlow 實現自編碼器
- 六、RNN 和梯度消失或爆炸問題
- 七、TensorFlow GPU 配置
- 八、TFLearn
- 九、使用協同過濾的電影推薦
- 十、OpenAI Gym
- TensorFlow 深度學習實戰指南中文版
- 一、入門
- 二、深度神經網絡
- 三、卷積神經網絡
- 四、循環神經網絡介紹
- 五、總結
- 精通 TensorFlow 1.x
- 一、TensorFlow 101
- 二、TensorFlow 的高級庫
- 三、Keras 101
- 四、TensorFlow 中的經典機器學習
- 五、TensorFlow 和 Keras 中的神經網絡和 MLP
- 六、TensorFlow 和 Keras 中的 RNN
- 七、TensorFlow 和 Keras 中的用于時間序列數據的 RNN
- 八、TensorFlow 和 Keras 中的用于文本數據的 RNN
- 九、TensorFlow 和 Keras 中的 CNN
- 十、TensorFlow 和 Keras 中的自編碼器
- 十一、TF 服務:生產中的 TensorFlow 模型
- 十二、遷移學習和預訓練模型
- 十三、深度強化學習
- 十四、生成對抗網絡
- 十五、TensorFlow 集群的分布式模型
- 十六、移動和嵌入式平臺上的 TensorFlow 模型
- 十七、R 中的 TensorFlow 和 Keras
- 十八、調試 TensorFlow 模型
- 十九、張量處理單元
- TensorFlow 機器學習秘籍中文第二版
- 一、TensorFlow 入門
- 二、TensorFlow 的方式
- 三、線性回歸
- 四、支持向量機
- 五、最近鄰方法
- 六、神經網絡
- 七、自然語言處理
- 八、卷積神經網絡
- 九、循環神經網絡
- 十、將 TensorFlow 投入生產
- 十一、更多 TensorFlow
- 與 TensorFlow 的初次接觸
- 前言
- 1.?TensorFlow 基礎知識
- 2. TensorFlow 中的線性回歸
- 3. TensorFlow 中的聚類
- 4. TensorFlow 中的單層神經網絡
- 5. TensorFlow 中的多層神經網絡
- 6. 并行
- 后記
- TensorFlow 學習指南
- 一、基礎
- 二、線性模型
- 三、學習
- 四、分布式
- TensorFlow Rager 教程
- 一、如何使用 TensorFlow Eager 構建簡單的神經網絡
- 二、在 Eager 模式中使用指標
- 三、如何保存和恢復訓練模型
- 四、文本序列到 TFRecords
- 五、如何將原始圖片數據轉換為 TFRecords
- 六、如何使用 TensorFlow Eager 從 TFRecords 批量讀取數據
- 七、使用 TensorFlow Eager 構建用于情感識別的卷積神經網絡(CNN)
- 八、用于 TensorFlow Eager 序列分類的動態循壞神經網絡
- 九、用于 TensorFlow Eager 時間序列回歸的遞歸神經網絡
- TensorFlow 高效編程
- 圖嵌入綜述:問題,技術與應用
- 一、引言
- 三、圖嵌入的問題設定
- 四、圖嵌入技術
- 基于邊重構的優化問題
- 應用
- 基于深度學習的推薦系統:綜述和新視角
- 引言
- 基于深度學習的推薦:最先進的技術
- 基于卷積神經網絡的推薦
- 關于卷積神經網絡我們理解了什么
- 第1章概論
- 第2章多層網絡
- 2.1.4生成對抗網絡
- 2.2.1最近ConvNets演變中的關鍵架構
- 2.2.2走向ConvNet不變性
- 2.3時空卷積網絡
- 第3章了解ConvNets構建塊
- 3.2整改
- 3.3規范化
- 3.4匯集
- 第四章現狀
- 4.2打開問題
- 參考
- 機器學習超級復習筆記
- Python 遷移學習實用指南
- 零、前言
- 一、機器學習基礎
- 二、深度學習基礎
- 三、了解深度學習架構
- 四、遷移學習基礎
- 五、釋放遷移學習的力量
- 六、圖像識別與分類
- 七、文本文件分類
- 八、音頻事件識別與分類
- 九、DeepDream
- 十、自動圖像字幕生成器
- 十一、圖像著色
- 面向計算機視覺的深度學習
- 零、前言
- 一、入門
- 二、圖像分類
- 三、圖像檢索
- 四、對象檢測
- 五、語義分割
- 六、相似性學習
- 七、圖像字幕
- 八、生成模型
- 九、視頻分類
- 十、部署
- 深度學習快速參考
- 零、前言
- 一、深度學習的基礎
- 二、使用深度學習解決回歸問題
- 三、使用 TensorBoard 監控網絡訓練
- 四、使用深度學習解決二分類問題
- 五、使用 Keras 解決多分類問題
- 六、超參數優化
- 七、從頭開始訓練 CNN
- 八、將預訓練的 CNN 用于遷移學習
- 九、從頭開始訓練 RNN
- 十、使用詞嵌入從頭開始訓練 LSTM
- 十一、訓練 Seq2Seq 模型
- 十二、深度強化學習
- 十三、生成對抗網絡
- TensorFlow 2.0 快速入門指南
- 零、前言
- 第 1 部分:TensorFlow 2.00 Alpha 簡介
- 一、TensorFlow 2 簡介
- 二、Keras:TensorFlow 2 的高級 API
- 三、TensorFlow 2 和 ANN 技術
- 第 2 部分:TensorFlow 2.00 Alpha 中的監督和無監督學習
- 四、TensorFlow 2 和監督機器學習
- 五、TensorFlow 2 和無監督學習
- 第 3 部分:TensorFlow 2.00 Alpha 的神經網絡應用
- 六、使用 TensorFlow 2 識別圖像
- 七、TensorFlow 2 和神經風格遷移
- 八、TensorFlow 2 和循環神經網絡
- 九、TensorFlow 估計器和 TensorFlow HUB
- 十、從 tf1.12 轉換為 tf2
- TensorFlow 入門
- 零、前言
- 一、TensorFlow 基本概念
- 二、TensorFlow 數學運算
- 三、機器學習入門
- 四、神經網絡簡介
- 五、深度學習
- 六、TensorFlow GPU 編程和服務
- TensorFlow 卷積神經網絡實用指南
- 零、前言
- 一、TensorFlow 的設置和介紹
- 二、深度學習和卷積神經網絡
- 三、TensorFlow 中的圖像分類
- 四、目標檢測與分割
- 五、VGG,Inception,ResNet 和 MobileNets
- 六、自編碼器,變分自編碼器和生成對抗網絡
- 七、遷移學習
- 八、機器學習最佳實踐和故障排除
- 九、大規模訓練
- 十、參考文獻
