七、TensorFlow 和 Keras 中的用于時間序列數據的 RNN · ApacheCN 深度學習譯文集

# 七、TensorFlow 和 Keras 中的用于時間序列數據的 RNN 時間序列數據是一系列值，以不同的時間間隔記錄或測量。作為序列，RNN 架構是從這些數據訓練模型的最佳方法。在本章中，我們將使用示例時間序列數據集來展示如何使用 TensorFlow 和 Keras 構建 RNN 模型。我們將在本章中介紹以下主題： * 航空公司乘客（`airpass`）時間序列數據集： * 描述和下載數據集 * 可視化數據集 * 在 TensorFlow 中預處理 RNN 的數據集 * TensorFlow 中用于時間序列數據的 RNN： * TensorFlow 中的`SimpleRNN` * TensorFlow 中的 LSTM * TensorFlow 中的 GRU * 在 Keras 中為 RNN 預處理數據集 * Keras 中用于時間序列數據的 RNN： * Keras 的`SimpleRNN` * Keras 的 LSTM * Keras 的 GRU 讓我們從了解樣本數據集開始。您可以按照 Jupyter 筆記本中的代碼`ch-07a_RNN_TimeSeries_TensorFlow`。 # 航空公司乘客數據集為了簡潔起見，我們選擇了一個名為國際航空公司乘客（航空通票）的非常小的數據集。該數據包含從 1949 年 1 月到 1960 年 12 月的每月總乘客數量。數據集中的數字是指數千的數量。該數據集最初由 Box 和 Jenkins 在 1976 年的工作中使用。它作為 **時間序列數據集庫**（**TSDL**）的一部分與 Rob Hyndman 教授的各種其他時間序列數據集一起收集。在澳大利亞莫納什大學。后來，TSDL 被轉移到 [DataMarket](http://datamarket.com)。 [您可以從此鏈接下載數據集](https://datamarket.com/data/set/22u3/international-airline-passengers-monthly-totals-in-thousands-jan-49-dec-60)。 # 加載 airpass 數據集我們將數據集保存為數據集根目錄（`~/datasets`）中`ts-data`文件夾中的 CSV 文件，并使用以下命令將數據加載到 pandas 數據框中： ```py filepath = os.path.join(datasetslib.datasets_root, 'ts-data', 'international-airline-passengers-cleaned.csv' ) dataframe = pd.read_csv(filepath,usecols=[1],header=0) dataset = dataframe.values dataset = dataset.astype(np.float32) ``` 從 NumPy 數組中的數據框中提取值并轉換為`np.float32`： ```py dataset = dataframe.values dataset = dataset.astype(np.float32) ``` # 可視化 airpass 數據集讓我們看一下數據集的外觀： ```py plt.plot(dataset,label='Original Data') plt.legend() plt.show() ``` `airpass`數據集的圖如下所示： ![](https://img.kancloud.cn/42/3a/423ac636198e460e377356aea74d8eb9_923x610.png)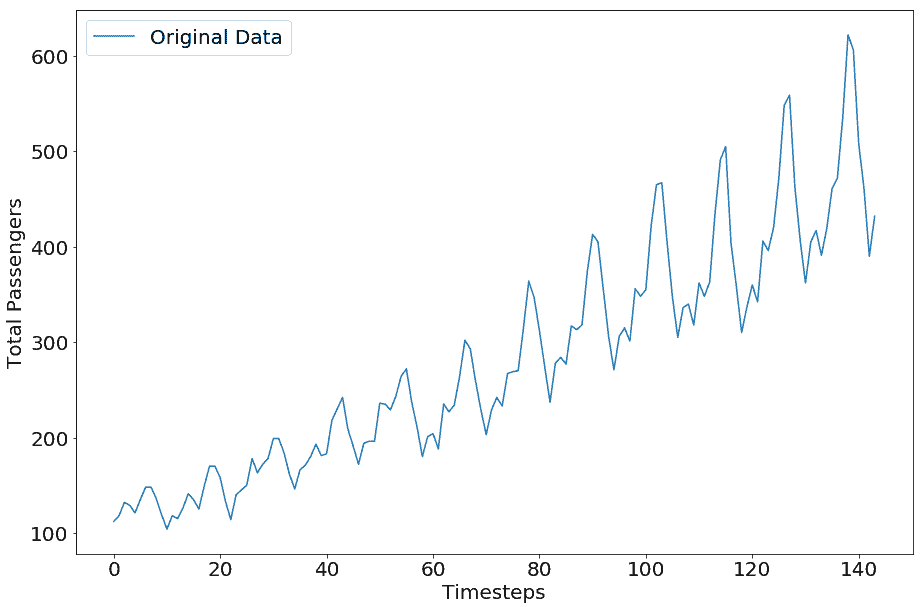Airline Passengers Dataset # 用于 TensorFlow RNN 模型的數據集預處理為了使其為學習模型做好準備，通過應用 MinMax 縮放來正則化數據集，該縮放使數據集值介于 0 和 1 之間。您可以嘗試根據數據的性質對數據應用不同的縮放方法。 ```py # normalize the dataset scaler = skpp.MinMaxScaler(feature_range=(0, 1)) normalized_dataset = scaler.fit_transform(dataset) ``` 我們使用自己開發的實用函數將數據集拆分為訓練和測試數據集。必須拆分數據而不對數據集進行混洗，因為改組數據集會破壞序列。維護數據序列對于訓練時間序列模型非常重要。 ```py train,test=tsu.train_test_split(normalized_dataset,train_size=0.67) ``` 然后我們將訓練和測試數據集轉換為有監督的機器學習集。讓我們試著理解監督學習集的含義。假設我們有一系列數據：`1,2,3,4,5`。我們想要了解生成數據集的概率分布。為了做到這一點，我們可以假設時間步長`t`的值是從時間步長`t-1`到`tk`的值的結果，其中`k`是窗口大小。為簡化起見，假設窗口大小為 1。因此，時間步長`t`的值（稱為輸入特征）是時間步長值`t-1`的結果，被稱為目標。讓我們重復一遍所有時間步驟，我們得到下表： | 輸入值或特征 | 輸出值或目標 | | --- | --- | | 1 | 2 | | 2 | 3 | | 3 | 4 | | 4 | 5 | 我們展示的示例只有一個變量值，它將轉換為特征和目標。當目標值取決于一個變量時，它被稱為單變量時間序列。同樣的邏輯可以應用于多變量時間序列，其中目標取決于多個變量。我們使用`x`來表示輸入特征，使用`y`來表示輸出目標。考慮到這一背景，為了將`airpass`數據轉換為監督機器學習數據，我們設置了以下超參數： 1. 設置用于學習或預測下一個時間步的過去時間步數： ```py n_x=1 ``` 1. 設置學習或預測的未來時間步長的數量： ```py n_y=1 ``` 1. 設置用于學習的`x`變量的數量；由于當前示例是單變量的，因此設置為 1： ```py n_x_vars = 1 ``` 1. 設置要預測的`y`變量的數量；由于當前示例是單變量的，因此設置為 1： ```py n_y_vars = 1 ``` 1. 最后，我們通過應用本節開頭所述的邏輯將訓練和測試數據集轉換為`X`和`Y`集： ```py X_train, Y_train, X_test, Y_test = tsu.mvts_to_xy(train, test,n_x=n_x,n_y=n_y) ``` 現在數據已經過預處理并可以輸入到我們的模型中，讓我們使用 TensorFlow 準備一個`SimpleRNN`模型。 # TensorFlow 中的簡單 RNN 在 TensorFlow 中定義和訓練簡單 RNN 的工作流程如下： 1. 定義模型的超參數： ```py state_size = 4 n_epochs = 100 n_timesteps = n_x learning_rate = 0.1 ``` 這里新的超參數是`state_size`。`state_size`表示 RNN 單元的權重向量的數量。 1. 為模型定義`X`和`Y`參數的占位符。`X`占位符的形狀為`(batch_size, number_of_input_timesteps, number_of_inputs)`，`Y`占位符的形狀為`(batch_size, number_of_output_timesteps, number_of_outputs)`。對于`batch_size`，我們使用`None`，以便我們以后可以輸入任意大小的批次。 ```py X_p = tf.placeholder(tf.float32, [None, n_timesteps, n_x_vars], name='X_p') Y_p = tf.placeholder(tf.float32, [None, n_timesteps, n_y_vars], name='Y_p') ``` 1. 將輸入占位符`X_p`轉換為長度等于時間步數的張量列表，在此示例中為`n_x`或 1： ```py # make a list of tensors of length n_timesteps rnn_inputs = tf.unstack(X_p,axis=1) ``` 1. 使用`tf.nn.rnn_cell.BasicRNNCell`創建一個簡單的 RNN 單元： ```py cell = tf.nn.rnn_cell.BasicRNNCell(state_size) ``` 1. TensorFlow 提供`static_rnn`和`dynamic_rnn`便利方法（以及其他方法）分別創建靜態和動態 RNN。創建靜態 RNN： ```py rnn_outputs, final_state = tf.nn.static_rnn(cell, rnn_inputs, dtype=tf.float32 ) ``` 靜態 RNN 在編譯時創建單元，即展開循環。動態 RNN 創建單元，即在運行時展開循環。在本章中，我們僅展示了`static_rnn`的示例，但是一旦獲得靜態 RNN 的專業知識，就應該探索`dynamic_rnn`。 `static_rnn`方法采用以下參數： * `cell`：我們之前定義的基本 RNN 單元對象。它可能是另一種單元，我們將在本章中進一步看到。 * `rnn_inputs`：形狀`(batch_size, number_of_inputs)`的張量列表。 * `dtype`：初始狀態和預期輸出的數據類型。 1. 定義預測層的權重和偏差參數： ```py W = tf.get_variable('W', [state_size, n_y_vars]) b = tf.get_variable('b', [n_y_vars], initializer=tf.constant_initializer(0.0)) ``` 1. 將預測層定義為密集線性層： ```py predictions = [tf.matmul(rnn_output, W) + b \ for rnn_output in rnn_outputs] ``` 1. 輸出 Y 是張量的形狀；將其轉換為張量列表： ```py y_as_list = tf.unstack(Y_p, num=n_timesteps, axis=1) ``` 1. 將損失函數定義為預測標簽和實際標簽之間的均方誤差： ```py mse = tf.losses.mean_squared_error losses = [mse(labels=label, predictions=prediction) for prediction, label in zip(predictions, y_as_list) ] ``` 1. 將總損失定義為所有預測時間步長的平均損失： ```py total_loss = tf.reduce_mean(losses) ``` 1. 定義優化器以最小化`total_loss`： ```py optimizer = tf.train.AdagradOptimizer(learning_rate).minimize(total_loss) ``` 1. 現在我們已經定義了模型，損耗和優化器函數，讓我們訓練模型并計算訓練損失： ```py with tf.Session() as tfs: tfs.run(tf.global_variables_initializer()) epoch_loss = 0.0 for epoch in range(n_epochs): feed_dict={X_p: X_train.reshape(-1, n_timesteps, n_x_vars), Y_p: Y_train.reshape(-1, n_timesteps, n_x_vars) } epoch_loss,y_train_pred,_=tfs.run([total_loss,predictions, optimizer], feed_dict=feed_dict) print("train mse = {}".format(epoch_loss)) ``` 我們得到以下值： ```py train mse = 0.0019413739209994674 ``` 1. 讓我們在測試數據上測試模型： ```py feed_dict={X_p: X_test.reshape(-1, n_timesteps,n_x_vars), Y_p: Y_test.reshape(-1, n_timesteps,n_y_vars) } test_loss, y_test_pred = tfs.run([total_loss,predictions], feed_dict=feed_dict ) print('test mse = {}'.format(test_loss)) print('test rmse = {}'.format(math.sqrt(test_loss))) ``` 我們在測試數據上得到以下 mse 和 rmse（均方根誤差）： ```py test mse = 0.008790395222604275 test rmse = 0.09375710758446143 ``` 這非常令人印象深刻。這是一個非常簡單的例子，只用一個變量值預測一個時間步。在現實生活中，輸出受到多個特征的影響，并且需要預測不止一個時間步。后一類問題被稱為多變量多時間步進預測問題。這些問題是使用循環神經網絡進行更好預測的積極研究領域。現在讓我們重新調整預測和原始值并繪制原始值（請在筆記本中查找代碼）。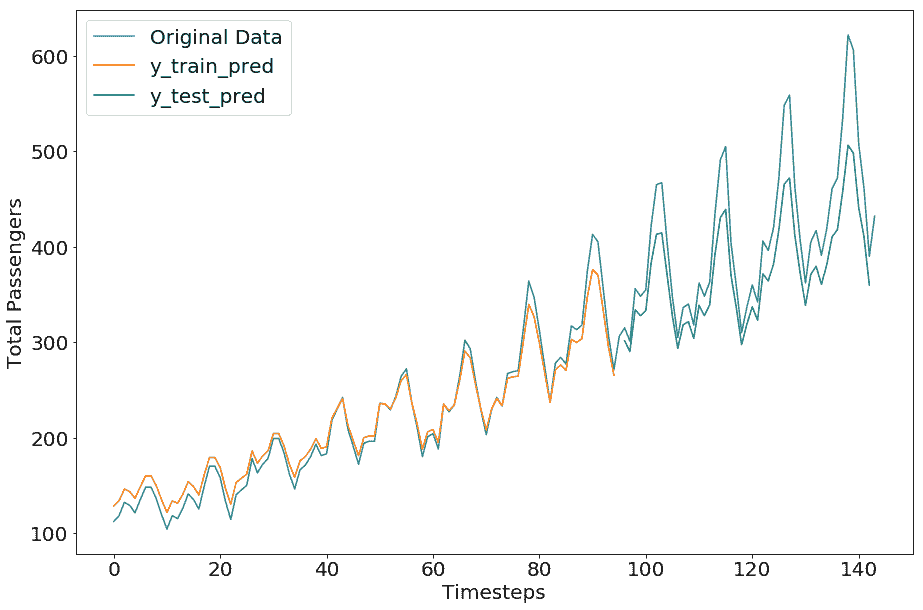我們得到以下繪圖： ![](https://img.kancloud.cn/68/ed/68eda0faf0b9085c6ca1a412061aa36c_923x610.png) 令人印象深刻的是，在我們的簡單示例中，預測數據幾乎與原始數據相匹配。對這種準確預測的一種可能解釋是，單個時間步的預測基于來自最后一個時間步的單個變量的預測，因此它們總是在先前值的附近。盡管如此，前面示例的目的是展示在 TensorFlow 中創建 RNN 的方法。現在讓我們使用 RNN 變體重新創建相同的示例。 # TensorFlow 中的 LSTM 由于爆炸和消失梯度的問題，簡單的 RNN 架構并不總是有效，因此使用了改進的 RNN 架構，例如 LSTM 網絡。 TensorFlow 提供 API 來創建 LSTM RNN 架構。在上一節中展示的示例中，要將簡單 RNN 更改為 LSTM 網絡，我們所要做的就是更改單元類型，如下所示： ```py cell = tf.nn.rnn_cell.LSTMCell(state_size) ``` 其余代碼保持不變，因為 TensorFlow 會為您在 LSTM 單元內創建門。筆記本`ch-07a_RNN_TimeSeries_TensorFlow`中提供了 LSTM 模型的完整代碼。然而，對于 LSTM，我們必須運行 600 個周期的代碼才能使結果更接近基本 RNN。原因是 LSTM 需要學習更多參數，因此需要更多的訓練迭代。對于我們的簡單示例，它似乎有點過分，但對于較大的數據集，與簡單的 RNN 相比，LSTM 顯示出更好的結果。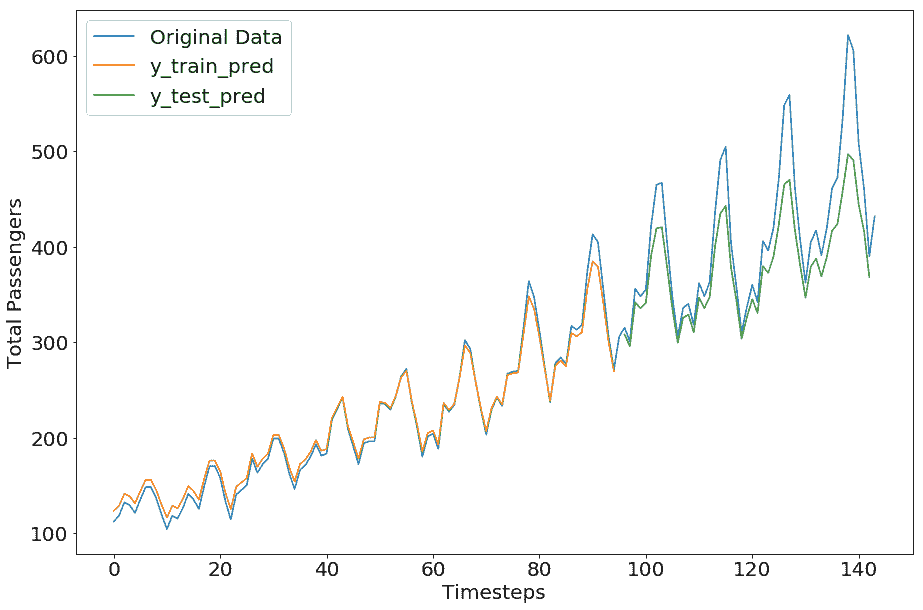具有 LSTM 架構的模型的輸出如下： ```py train mse = 0.0020806745160371065 test mse = 0.01499235536903143 test rmse = 0.12244327408653947 ``` ![](https://img.kancloud.cn/28/7b/287b8f2cf8db72517a962a5f15bbd66e_923x610.png) # TensorFlow 中的 GRU 要將最后一節中的 LSTM 示例更改為 GRU 網絡，按如下方式更改單元類型，TensorFlow 將為您處理其余部分： ```py cell = tf.nn.rnn_cell.GRUCell(state_size) ``` 筆記本`ch-07a_RNN_TimeSeries_TensorFlow`中提供了 GRU 模型的完整代碼。對于小`airpass`數據集，GRU 在相同數量的周期中表現出更好的表現。在實踐中，GRU 和 LSTM 表現出相當的表現。就執行速度而言，與 LSTM 相比，GRU 模型訓練和預測更快。 GRU 模型的完整代碼在 Jupyter 筆記本中提供。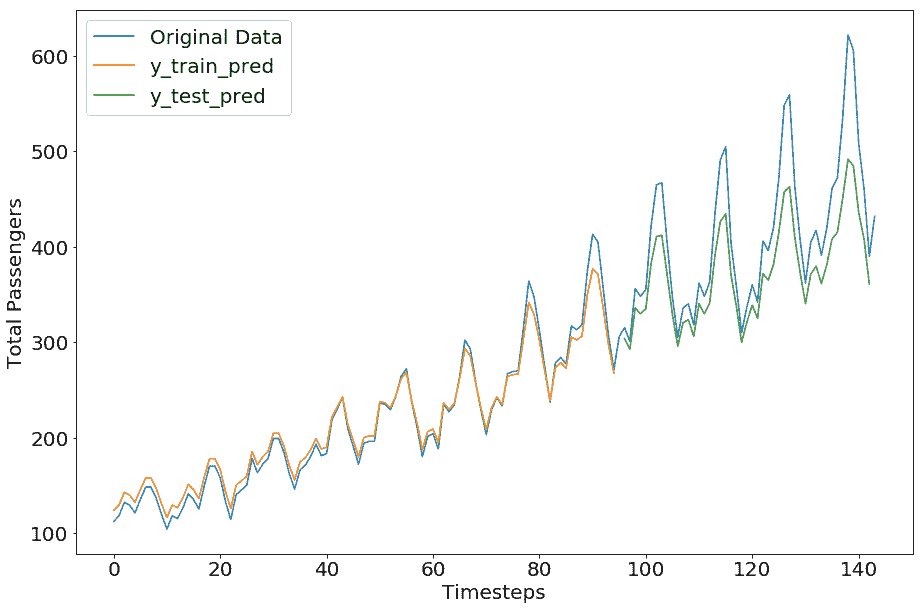GRU 模型的結果如下： ```py train mse = 0.0019633215852081776 test mse = 0.014307591132819653 test rmse = 0.11961434334066987 ``` ![](https://img.kancloud.cn/8f/04/8f044d43dad4c7695853e4dc31d9fbf2_923x610.png) 我們鼓勵您探索 TensorFlow 中可用的其他選項來創建循環神經網絡。現在讓我們在 TensorFlow 的一個高級庫中嘗試相同的示例。對于下一節，您可以按照 Jupyter 筆記本中的代碼`ch-07b_RNN_TimeSeries_Keras`。 # 用于 Keras RNN 模型的數據集預處理與使用較低級別 TensorFlow 類和方法構建相比，在 Keras 中構建 RNN 網絡要簡單得多。對于 Keras，我們預先處理數據，如前面部分所述，以獲得受監督的機器學習時間序列數據集：`X_train, Y_train, X_test, Y_test`。從這里開始，預處理有所不同。對于 Keras，輸入必須是`(samples, time steps, features)`形狀。當我們將數據轉換為監督機器學習格式時，在重塑數據時，我們可以將時間步長設置為 1，從而將所有輸入時間步長作為特征，或者我們可以設置時間步長為實際的時間步數，從而為每個時間步長提供特征集。換句話說，我們之前獲得的`X_train`和`X_test`數據集可以重新整形為以下方法之一：方法 1：`n`時間步長與`1`特征： ```py X_train.reshape(X_train.shape[0], X_train.shape[1],1) ``` 方法 2：`1`時間步長`n`特征： ```py X_train.reshape(X_train.shape[0], 1, X_train.shape[1]) ``` 在本章中，我們將對特征大小為 1 的數據集進行整形，因為我們只使用一個變量作為輸入： ```py # reshape input to be [samples, time steps, features] X_train = X_train.reshape(X_train.shape[0], X_train.shape[1],1) X_test = X_test.reshape(X_test.shape[0], X_train.shape[1], 1) ``` # Keras 中的簡單 RNN 通過添加具有內部神經元數量和輸入張量形狀的`SimpleRNN`層，可以在 Keras 中輕松構建 RNN 模型，不包括樣本維數。以下代碼創建，編譯和擬合`SimpleRNN`： ```py # create and fit the SimpleRNN model model = Sequential() model.add(SimpleRNN(units=4, input_shape=(X_train.shape[1], X_train.shape[2]))) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') model.fit(X_train, Y_train, epochs=20, batch_size=1) ``` 由于我們的數據集很小，我們使用`batch_size`為 1 并訓練 20 次迭代，但對于較大的數據集，您需要調整這些和其他超參數的值。該模型的結構如下： ```py _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= simple_rnn_1 (SimpleRNN) (None, 4) 24 _________________________________________________________________ dense_1 (Dense) (None, 1) 5 ================================================================= Total params: 29 Trainable params: 29 Non-trainable params: 0 ``` 訓練的結果如下： ```py Epoch 1/20 95/95 [==============================] - 0s - loss: 0.0161 Epoch 2/20 95/95 [==============================] - 0s - loss: 0.0074 Epoch 3/20 95/95 [==============================] - 0s - loss: 0.0063 Epoch 4/20 95/95 [==============================] - 0s - loss: 0.0051 -- epoch 5 to 14 removed for the sake of brevity -- Epoch 14/20 95/95 [==============================] - 0s - loss: 0.0021 Epoch 15/20 95/95 [==============================] - 0s - loss: 0.0020 Epoch 16/20 95/95 [==============================] - 0s - loss: 0.0020 Epoch 17/20 95/95 [==============================] - 0s - loss: 0.0020 Epoch 18/20 95/95 [==============================] - 0s - loss: 0.0020 Epoch 19/20 95/95 [==============================] - 0s - loss: 0.0020 Epoch 20/20 95/95 [==============================] - 0s - loss: 0.0020 ``` 損失從 0.0161 開始，平穩在 0.0020。讓我們做出預測并重新調整預測和原件。我們使用 Keras 提供的函數來計算均方根誤差： ```py from keras.losses import mean_squared_error as k_mse from keras.backend import sqrt as k_sqrt import keras.backend as K # make predictions y_train_pred = model.predict(X_train) y_test_pred = model.predict(X_test) # invert predictions y_train_pred = scaler.inverse_transform(y_train_pred) y_test_pred = scaler.inverse_transform(y_test_pred) #invert originals y_train_orig = scaler.inverse_transform(Y_train) y_test_orig = scaler.inverse_transform(Y_test) # calculate root mean squared error trainScore = k_sqrt(k_mse(y_train_orig[:,0], y_train_pred[:,0]) ).eval(session=K.get_session()) print('Train Score: {0:.2f} RMSE'.format(trainScore)) testScore = k_sqrt(k_mse(y_test_orig[:,0], y_test_pred[:,0]) ).eval(session=K.get_session()) print('Test Score: {0:.2f} RMSE'.format(testScore)) ``` 我們得到以下結果： ```py Train Score: 23.27 RMSE Test Score: 54.13 RMSE ``` ![](https://img.kancloud.cn/38/52/3852a234f04d6ddde82326fa939b4b18_923x610.png) 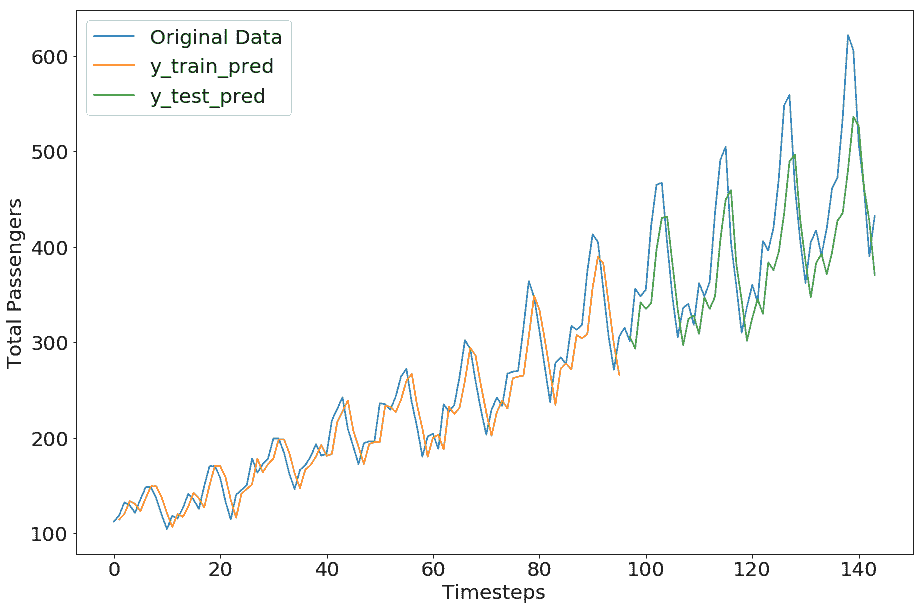我們可以看到，這不像我們在 TensorFlow 部分得到的那樣完美；但是，這種差異是因為超參數值。我們留給您嘗試不同的超參數值來調整此 Keras 模型以獲得更好的結果。 # Keras 中的 LSTM 創建 LSTM 模型只需添加 LSTM 層而不是`SimpleRNN`層，如下所示： ```py model.add(LSTM(units=4, input_shape=(X_train.shape[1], X_train.shape[2]))) ``` 模型結構如下所示： ```py _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= lstm_1 (LSTM) (None, 4) 96 _________________________________________________________________ dense_1 (Dense) (None, 1) 5 ================================================================= Total params: 101 Trainable params: 101 Non-trainable params: 0 _________________________________________________________________ ``` 筆記本`ch-07b_RNN_TimeSeries_Keras`中提供了 LSTM 模型的完整代碼。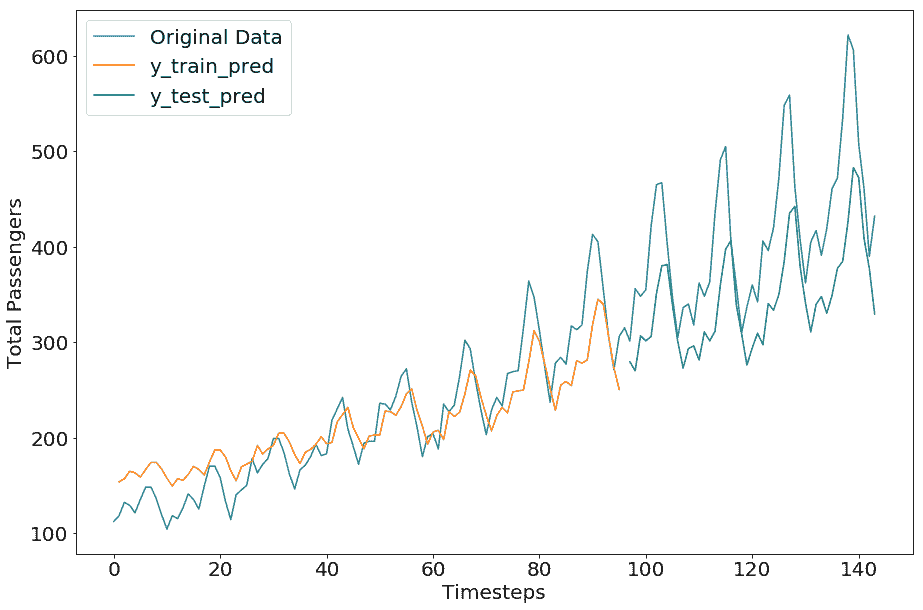由于 LSTM 模型具有更多需要訓練的參數，對于相同數量的迭代（20 個周期），我們得到更高的誤差分數。我們留給您探索周期和其他超參數的各種值，以獲得更好的結果： ```py Train Score: 32.21 RMSE Test Score: 84.68 RMSE ``` ![](https://img.kancloud.cn/f8/5a/f85a12af2372baafadb51b7479f6f7bf_923x610.png) # Keras 中的 GRU 使用 TensorFlow 和 Keras 的一個優點是它們可以輕松創建模型。與 LSTM 一樣，創建 GRU 模型只需添加 GRU 層而不是 LSTM 或`SimpleRNN`層，如下所示： ```py model.add(GRU(units=4, input_shape=(X_train.shape[1], X_train.shape[2]))) ``` 模型結構如下： ```py Layer (type) Output Shape Param # ================================================================= gru_1 (GRU) (None, 4) 72 _________________________________________________________________ dense_1 (Dense) (None, 1) 5 ================================================================= Total params: 77 Trainable params: 77 Non-trainable params: 0 ``` 筆記本`ch-07b_RNN_TimeSeries_Keras`中提供了 GRU 模型的完整代碼。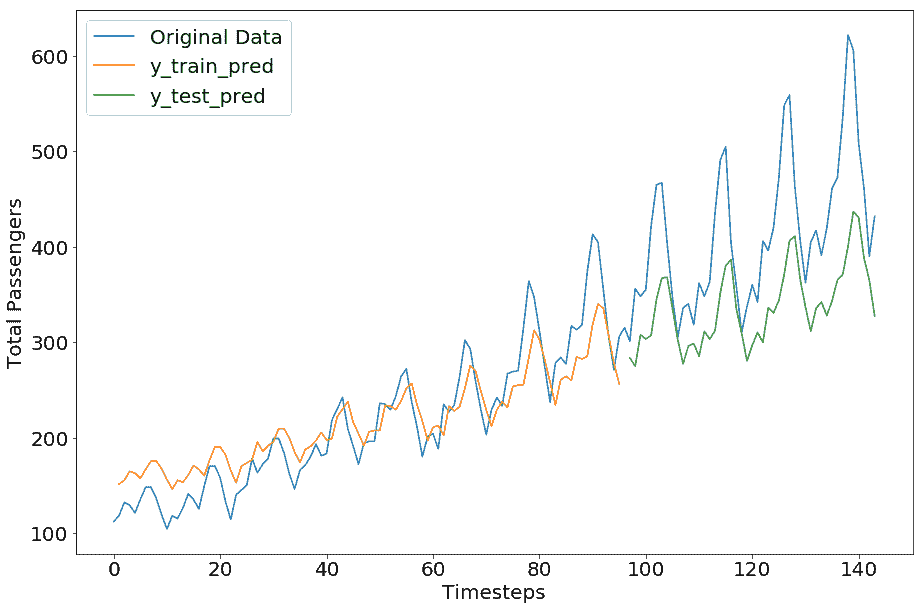正如預期的那樣，GRU 模型顯示出與 LSTM 幾乎相同的表現，我們讓您嘗試使用不同的超參數值來優化此模型： ```py Train Score: 31.49 RMSE Test Score: 92.75 RMSE ``` ![](https://img.kancloud.cn/a8/41/a8410aa05a7cdefa8209a77e4d0ce814_923x610.png) # 總結時間序列數據是基于序列的數據，因此 RNN 模型是從時間序列數據中學習的相關架構。在本章中，您學習了如何使用 TensorFlow（一個低級庫）和 Keras（一個高級庫）創建不同類型的 RNN 模型。我們只介紹了`SimpleRNN`，LSTM 和 GRU，但您應該探索可以使用 TensorFlow 和 Keras 創建的許多其他 RNN 變體。在下一章中，我們將使用當前章節和前幾章中構建的基礎為各種**自然語言處理**（**NLP**）任務創建文本數據的 RNN 模型。