# 三、實現前饋神經網絡 自動識別手寫數字是一個重要的問題，可以在許多實際應用中找到。在本節中，我們將實現一個前饋網絡來解決這個問題。  圖 3：從 MNIST 數據庫中提取的數據示例 為了訓練和測試已實現的模型，我們將使用一個名為 MNIST 的手寫數字最著名的數據集。 MNIST 數據集是一個包含 60,000 個示例的訓練集和一個包含 10,000 個示例的測試集。存儲在示例文件中的數據示例如上圖所示。 源圖像最初是黑白的。之后，為了將它們標準化為`20×20`像素的大小，由于抗混疊濾波器用于調整大小的效果，引入了中間亮度級別。隨后，在`28×28`像素的區域中將圖像聚焦在像素的質心中，以便改善學習過程。整個數據庫存儲在四個文件中： * `train-images-idx3-ubyte.gz`：訓練集圖像（9912422 字節） * `train-labels-idx1-ubyte.gz`：訓練集標簽（28881 字節） * `t10k-images-idx3-ubyte.gz`：測試集圖像（1648877 字節） * `t10k-labels-idx1-ubyte.gz`：測試集標簽（4542 字節） 每個數據庫包含兩個文件的 ;第一個包含圖像，而第二個包含相應的標簽。 ## 探索 MNIST 數據集 讓我們看一下如何訪問 MNIST 數據的簡短示例，以及如何顯示所選圖像。為此，只需執行`Explore_MNIST.py`腳本。首先，我們必須導入 numpy，因為我們必須進行一些圖像處理： ```py import numpy as np ``` Matplotlib 中的`pyplot`函數用于繪制圖像： ```py import matplotlib.pyplot as plt ``` 我們將使用`tensorflow.examples.tutorials.mnist`中的`input_data`類，它允許我們下載 MNIST 數據庫并構建數據集： ```py import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data ``` 然后我們使用`read_data_sets`方法加載數據集： ```py import os dataPath = "temp/" if not os.path.exists(dataPath): os.makedirs(dataPath) input = input_data.read_data_sets(dataPath, one_hot=True) ``` 圖像將保存在`temp/`目錄中。現在讓我們看看圖像和標簽的形狀： ```py print(input.train.images.shape) print(input.train.labels.shape) print(input.test.images.shape) print(input.test.labels.shape) ``` 以下是上述代碼的輸出： ```py >>> (55000, 784) (55000, 10) (10000, 784) (10000, 10) ``` 使用 Python 庫`matplotlib`，我們想要可視化一個數字： ```py image_0 = input.train.images[0] image_0 = np.resize(image_0,(28,28)) label_0 = input.train.labels[0] print(label_0) ``` 以下是上述代碼的輸出： ```py >>> [ 0\. 0\. 0\. 0\. 0\. 0\. 0\. 1\. 0\. 0.] ``` 數字`1`是數組的第八個位置。這意味著我們圖像的數字是數字 7。最后，我們必須驗證數字是否真的是 7。我們可以使用導入的`plt`函數來繪制`image_0`張量： ```py plt.imshow(image_0, cmap='Greys_r') plt.show() ```  圖 4：從 MNIST 數據集中提取的圖像 ### Softmax 分類器 在上一節中，我們展示了如何訪問和操作 MNIST 數據集。在本節中，我們將看到如何使用前面的數據集來解決 TensorFlow 手寫數字的分類問題。我們將應用所學的概念來構建更多神經網絡模型，以便評估和比較所采用的不同方法的結果。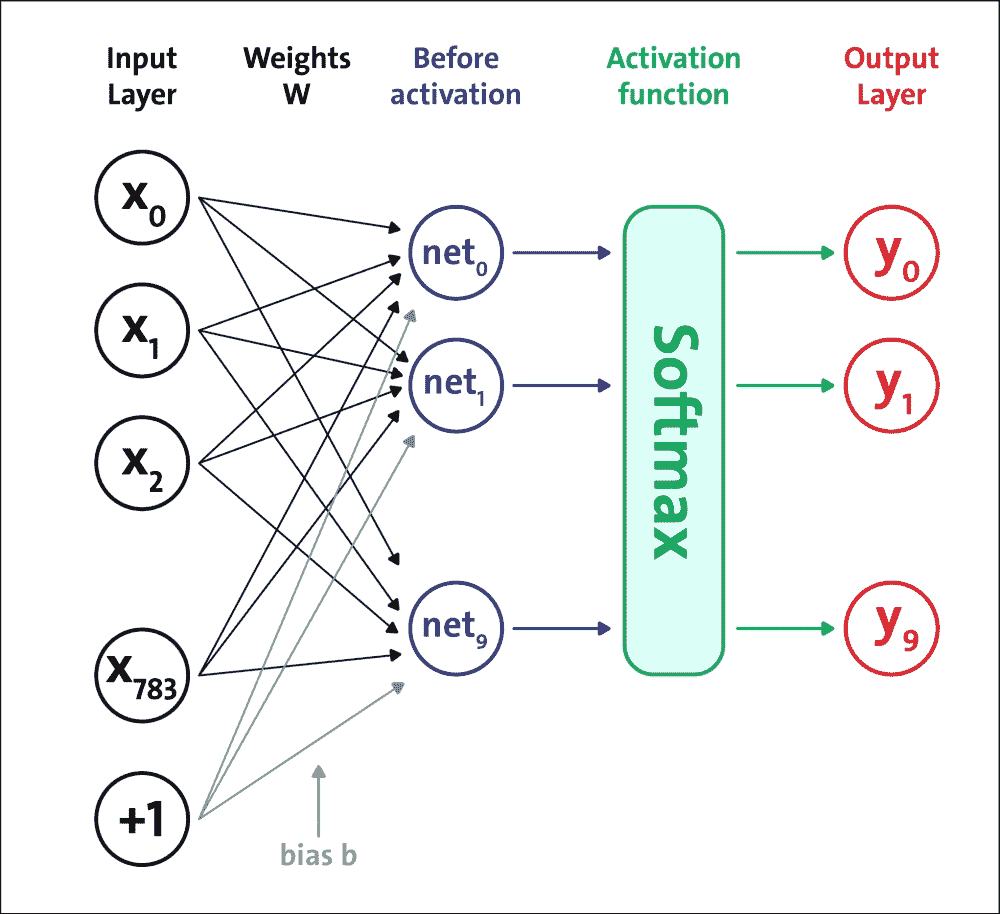 將要實現的第一個前饋網絡架構如下圖所示：  圖 5：softmax 神經網絡架構 我們將構建一個五層網絡：第一層到第四層是 Sigmoid 結構，第五層是 softmax 激活函數。請記住，定義此網絡是為了激活它是一組正值，總和等于 1。這意味著輸出的第`j`個值是與網絡輸入對應的類`j`的概率。讓我們看看如何實現我們的神經網絡模型。 為了確定網絡的適當大小（即，層中的神經元或單元的數量），即隱藏層的數量和每層神經元的數量，通常我們依賴于一般的經驗標準，個人經驗或適當的測試。這些是需要調整的一些超參數。在本章的后面，我們將看到一些超參數優化的例子。 下表總結了已實現的網絡架構。它顯示了每層神經元的數量，以及相應的激活函數： | 層 | 神經元數量 | 激活函數 | | --- | --- | --- | | 1 | `L = 200` | Sigmoid | | 2 | `M = 100` | Sigmoid | | 3 | `N = 60` | Sigmoid | | 4 | `O = 30` | Sigmoid | | 5 | `10` | Softmax | 前四層的激活函數是 Sigmoid 函數。激活函數的最后一層始終是 softmax，因為網絡的輸出必須表示輸入數字的概率。通常，中間層的數量和大小會極大地影響的網絡表現： * 以積極的方式，因為在這些層上是基于網絡推廣的能力，并檢測輸入的特殊特征 * 以負面的方式，因為如果網絡是冗余的，那么它會不必要地減輕學習階段的負擔 為此，只需執行`five_layers_sigmoid.py`腳本。首先，我們將通過導入以下庫來開始實現網絡： ```py import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data import math from tensorflow.python.framework import ops import random import os ``` 接下來，我們將設置以下配置參數： ```py logs_path = 'log_sigmoid/' # logging path batch_size = 100 # batch size while performing training learning_rate = 0.003 # Learning rate training_epochs = 10 # training epoch display_epoch = 1 ``` 然后，我們將下載圖像和標簽，并準備數據集： ```py dataPath = "temp/" if not os.path.exists(dataPath): os.makedirs(dataPath) mnist = input_data.read_data_sets(dataPath, one_hot=True) # MNIST to be downloaded ``` 從輸入層開始，我們現在將看看如何構建網絡架構。輸入層現在是形狀`[1×784]`的張量 - 即`[1,28 * 28]`，它代表要分類的圖像： ```py X = tf.placeholder(tf.float32, [None, 784], name='InputData') # image shape 28*28=784 XX = tf.reshape(X, [-1, 784]) # reshape input Y_ = tf.placeholder(tf.float32, [None, 10], name='LabelData') # 0-9 digits => 10 classes ``` 第一層接收要分類的輸入圖像的像素，與`W1`權重連接組合，并添加到`B1`偏差張量的相應值： ```py W1 = tf.Variable(tf.truncated_normal([784, L], stddev=0.1)) # Initialize random weights for the hidden layer 1 B1 = tf.Variable(tf.zeros([L])) # Bias vector for layer 1 ``` 第一層通過 sigmoid 激活函數將其輸出發送到第二層： ```py Y1 = tf.nn.sigmoid(tf.matmul(XX, W1) + B1) # Output from layer 1 ``` 第二層從第一層接收`Y1`輸出，將其與`W2`權重連接組合，并將其添加到`B2`偏差張量的相應值： ```py W2 = tf.Variable(tf.truncated_normal([L, M], stddev=0.1)) # Initialize random weights for the hidden layer 2 B2 = tf.Variable(tf.ones([M])) # Bias vector for layer 2 ``` 第二層通過 sigmoid 激活函數將其輸出發送到第三層： ```py Y2 = tf.nn.sigmoid(tf.matmul(Y1, W2) + B2) # Output from layer 2 ``` 第三層接收來自第二層的`Y2`輸出，將其與`W3`權重連接組合，并將其添加到`B3`偏差張量的相應值： ```py W3 = tf.Variable(tf.truncated_normal([M, N], stddev=0.1)) # Initialize random weights for the hidden layer 3 B3 = tf.Variable(tf.ones([N])) # Bias vector for layer 3 ``` 第三層通過 sigmoid 激活函數將其輸出發送到第四層： ```py Y3 = tf.nn.sigmoid(tf.matmul(Y2, W3) + B3) # Output from layer 3 ``` 第四層接收來自第三層的`Y3`輸出，將其與`W4`權重連接組合，并將其添加到`B4`偏差張量的相應值： ```py W4 = tf.Variable(tf.truncated_normal([N, O], stddev=0.1)) # Initialize random weights for the hidden layer 4 B4 = tf.Variable(tf.ones([O])) # Bias vector for layer 4 ``` 然后通過 Sigmoid 激活函數將第四層的輸出傳播到第五層： ```py Y4 = tf.nn.sigmoid(tf.matmul(Y3, W4) + B4) # Output from layer 4 ``` 第五層將在輸入中接收來自第四層的激活`O = 30`，該激活將通過`softmax`激活函數，轉換為每個數字的相應概率類別： ```py W5 = tf.Variable(tf.truncated_normal([O, 10], stddev=0.1)) # Initialize random weights for the hidden layer 5 B5 = tf.Variable(tf.ones([10])) # Bias vector for layer 5 Ylogits = tf.matmul(Y4, W5) + B5 # computing the logits Y = tf.nn.softmax(Ylogits)# output from layer 5 ``` 這里，我們的損失函數是目標和`softmax`激活函數之間的交叉熵，應用于模型的預測： ```py cross_entropy = tf.nn.softmax_cross_entropy_with_logits_v2(logits=Ylogits, labels=Y) # final outcome using softmax cross entropy cost_op = tf.reduce_mean(cross_entropy)*100 ``` 另外，我們定義`correct_prediction`和模型的準確率： ```py correct_prediction = tf.equal(tf.argmax(Y, 1), tf.argmax(Y_, 1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) ``` 現在我們需要使用優化器來減少訓練誤差。與簡單的`GradientDescentOptimizer`相比，`AdamOptimizer`具有幾個優點。實際上，它使用更大的有效步長，算法將收斂到此步長而不進行微調： ```py # Optimization op (backprop) train_op = tf.train.AdamOptimizer(learning_rate).minimize(cost_op) ``` `Optimizer`基類提供了計算損失梯度的方法，并將梯度應用于變量。子類集合實現了經典的優化算法，例如`GradientDescent`和`Adagrad`。在 TensorFlow 中訓練 NN 模型時，我們從不實例化`Optimizer`類本身，而是實例化以下子類之一 * [`tf.train.Optimizer`](https://www.tensorflow.org/api_docs/python/tf/train/Optimizer) * [`tf.train.GradientDescentOptimizer`](https://www.tensorflow.org/api_docs/python/tf/train/GradientDescentOptimizer) * [`tf.train.AdadeltaOptimizer`](https://www.tensorflow.org/api_docs/python/tf/train/AdadeltaOptimizer) * [`tf.train.AdagradOptimizer`](https://www.tensorflow.org/api_docs/python/tf/train/AdagradOptimizer) * [`tf.train.AdagradDAOptimizer`](https://www.tensorflow.org/api_docs/python/tf/train/AdagradDAOptimizer) * [`tf.train.MomentumOptimizer`](https://www.tensorflow.org/api_docs/python/tf/train/MomentumOptimizer) * [`tf.train.AdamOptimizer`](https://www.tensorflow.org/api_docs/python/tf/train/AdamOptimizer) * [`tf.train.FtrlOptimizer`](https://www.tensorflow.org/api_docs/python/tf/train/FtrlOptimizer) * [`tf.train.ProximalGradientDescentOptimizer`](https://www.tensorflow.org/api_docs/python/tf/train/ProximalGradientDescentOptimizer) * [`tf.train.ProximalAdagradOptimizer`](https://www.tensorflow.org/api_docs/python/tf/train/ProximalAdagradOptimize) * [`tf.train.RMSPropOptimizer`](https://www.tensorflow.org/api_docs/python/tf/train/RMSPropOptimizer) 見[此鏈接](https://www.tensorflow.org/api_guides/python/train)和[`tf.contrib.opt`](https://www.tensorflow.org/api_docs/python/tf/contrib/opt)用于更多優化器。 然后讓我們構建一個將所有操作封裝到范圍中的模型，使 TensorBoard 的圖可視化更加方便： ```py # Create a summary to monitor cost tensor tf.summary.scalar("cost", cost_op) # Create a summary to monitor accuracy tensor tf.summary.scalar("accuracy", accuracy) # Merge all summaries into a single op summary_op = tf.summary.merge_all() ``` 最后，我們將開始訓練： ```py with tf.Session() as sess: # Run the initializer sess.run(init_op) # op to write logs to TensorBoard writer = tf.summary.FileWriter(logs_path, graph=tf.get_default_graph()) for epoch in range(training_epochs): batch_count = int(mnist.train.num_examples/batch_size) for i in range(batch_count): batch_x, batch_y = mnist.train.next_batch(batch_size) _,summary = sess.run([train_op, summary_op], feed_dict={X: batch_x, Y_: batch_y}) writer.add_summary(summary, epoch * batch_count + i) print("Epoch: ", epoch) print("Optimization Finished!") print("Accuracy: ", accuracy.eval(feed_dict={X: mnist.test.images, Y_: mnist.test.labels})) ``` 定義摘要和會話運行的源代碼幾乎與前一個相同。我們可以直接轉向評估實現的模型。運行模型時，我們有以下輸出： 運行此代碼后的最終測試設置準確率應約為 97%： ```py Extracting temp/train-images-idx3-ubyte.gz Extracting temp/train-labels-idx1-ubyte.gz Extracting temp/t10k-images-idx3-ubyte.gz Extracting temp/t10k-labels-idx1-ubyte.gz Epoch: 0 Epoch: 1 Epoch: 2 Epoch: 3 Epoch: 4 Epoch: 5 Epoch: 6 Epoch: 7 Epoch: 8 Epoch: 9 Optimization Finished! Accuracy: 0.9 715 ``` 現在我們可以通過在運行文件夾中打開終端然后執行以下命令來移動到 TensorBoard： ```py $> tensorboard --logdir='log_sigmoid/' # if required, provide absolute path ``` 然后我們在`localhost`上打開瀏覽器。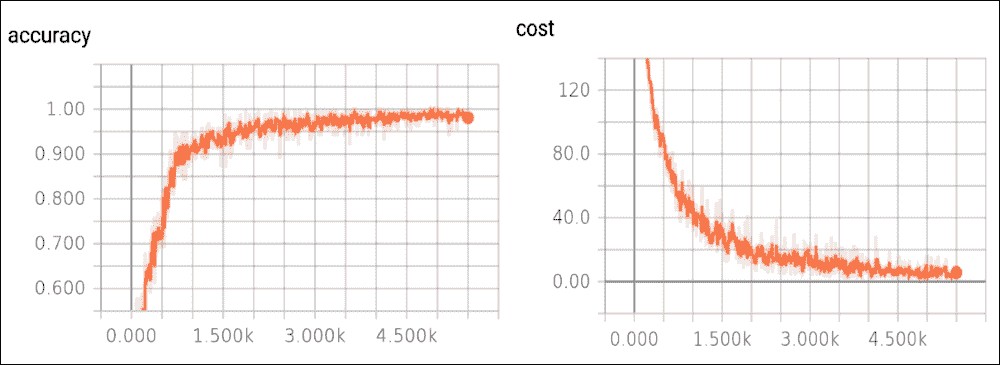在下圖中，我們顯示了成本函數的趨勢，作為示例數量的函數，在訓練集上，以及測試集的準確率：  圖 6：測試集上的準確率函數，以及訓練集上的成本函數 成本函數隨著迭代次數的增加而減少。如果沒有發生這種情況，則意味著出現了問題。在最好的情況下，這可能只是因為某些參數未正確設置。在最壞的情況下，構建的數據集中可能存在問題，例如，信息太少或圖像質量差。如果發生這種情況，我們必須直接修復數據集。 到目前為止，我們已經看到了 FFNN 的實現。但是，使用真實數據集探索更有用的 FFNN 實現會很棒。我們將從 MLP 開始。 # 實現多層感知器（MLP） 感知器單層 LTU 組成，每個神經元連接到所有輸入。這些連接通常使用稱為輸入神經元的特殊傳遞神經元來表示：它們只輸出它們被輸入的任何輸入。此外，通常添加額外的偏置特征（`x0 = 1`）。 這種偏置特征通常使用稱為偏置神經元的特殊類型的神經元來表示，一直輸出 1。具有兩個輸入和三個輸出的感知器在圖 7 中表示。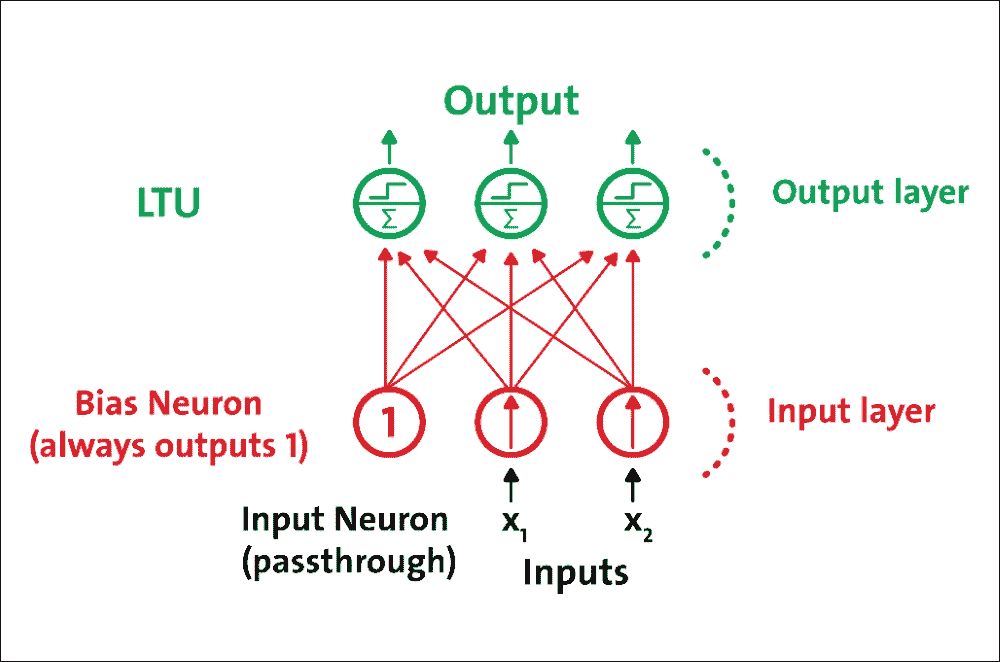該感知器可以同時將實例分類為三個不同的二元類，這使其成為多輸出分類器：  圖 7：具有兩個輸入和三個輸出的感知器 由于每個輸出神經元的決策邊界是線性的，因此感知器無法學習復雜模式。然而，如果訓練實例是線性可分的，研究表明該算法將收斂于稱為“感知器收斂定理”的解決方案。 MLP 是 FFNN，這意味著它是來自不同層的神經元之間的唯一連接。更具體地，MLP 由一個（通過）輸入層，一個或多個 LTU 層（稱為隱藏層）和一個稱為輸出層的 LTU 的最后一層組成。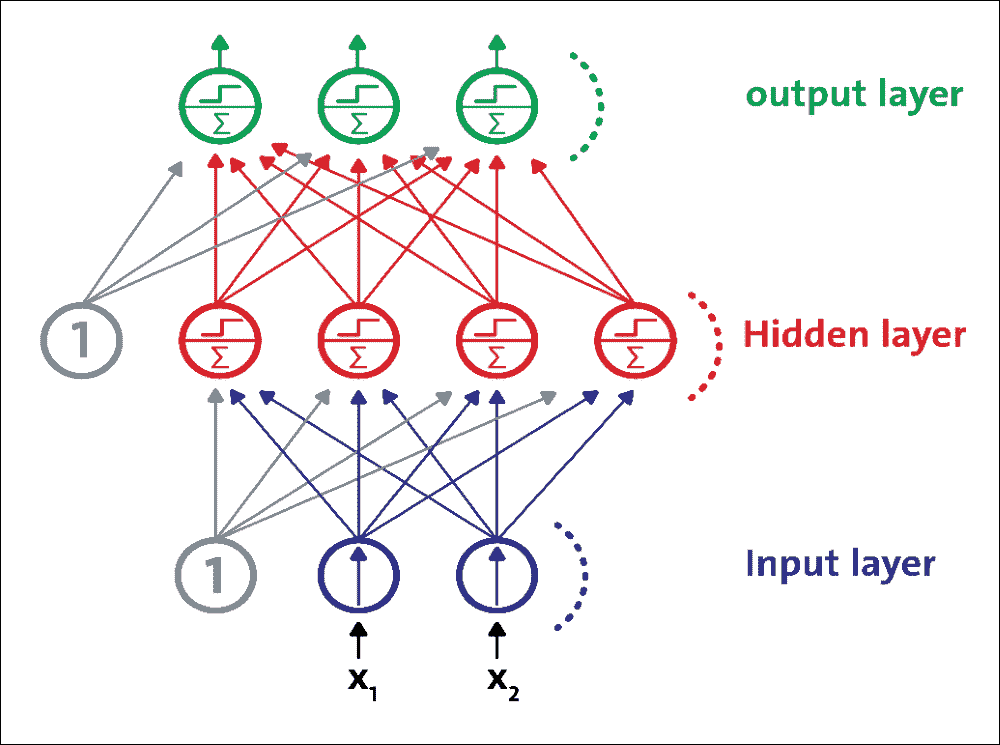除輸出層外，每一層都包含一個偏置神經元，并作為完全連接的二分圖連接到下一層：  圖 8：MLP 由一個輸入層，一個隱藏層和一個輸出層組成 ## 訓練 MLP MLP 在 1986 年首次使用反向傳播訓練算法成功訓練。然而，現在這種算法的優化版本被稱為梯度下降。在訓練階段期間，對于每個訓練實例，算法將其饋送到網絡并計算每個連續層中的每個神經元的輸出。 訓練算法測量網絡的輸出誤差（即，期望輸出和網絡的實際輸出之間的差異），并計算最后隱藏層中每個神經元對每個輸出神經元誤差的貢獻程度。然后，它繼續測量這些誤差貢獻中有多少來自先前隱藏層中的每個神經元，依此類推，直到算法到達輸入層。通過在網絡中向后傳播誤差梯度，該反向傳遞有效地測量網絡中所有連接權重的誤差梯度。 在技??術上，通過反向傳播方法計算每層的成本函數的梯度。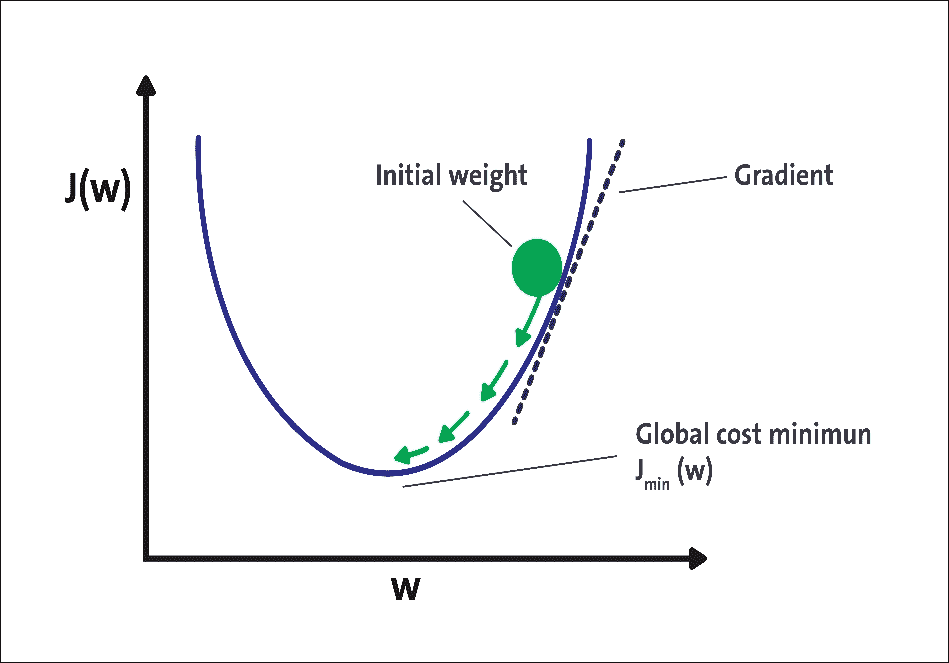梯度下降的想法是有一個成本函數，顯示某些神經網絡的預測輸出與實際輸出之間的差異：  圖 9：用于無監督學習的 ANN 的示例實現 有幾種已知類型的代價函數，例如平方誤差函數和對數似然函數。該成本函數的選擇可以基于許多因素。梯度下降法通過最小化此成本函數來優化網絡的權重。步驟如下： 1. 權重初始化 2. 計算神經網絡的預測輸出，通常稱為轉發傳播步驟 3. 計算成本/損失函數。一些常見的成本/損失函數包括對數似然函數和平方誤差函數 4. 計算成本/損失函數的梯度。對于大多數 DNN 架構，最常見的方法是反向傳播 5. 基于當前權重的權重更新，以及成本/損失函數的梯度 6. 步驟 2 到 5 的迭代，直到成本函數，達到某個閾值或經過一定量的迭代 圖 9 中可以看到梯度下降的圖示。該圖顯示了基于網絡權重的神經網絡的成本函數。在梯度下降的第一次迭代中，我們將成本函數應用于一些隨機初始權重。對于每次迭代，我們在梯度方向上更新權重，這對應于圖 9 中的箭頭。重復更新直到一定次數的迭代或直到成本函數達到某個閾值。 ## 使用 MLP 多層感知器通常用于以監督方式解決分類和回歸問題。盡管 CNN 逐漸取代了它們在圖像和視頻數據中的實現，但仍然可以有效地使用低維和數字特征 MLP：可以解決二元和多類分類問題。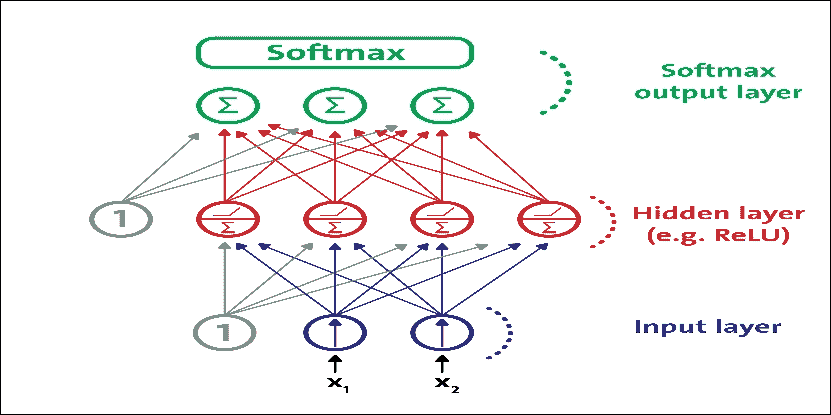  圖 10：用于分類的現代 MLP（包括 ReLU 和 softmax） 然而，對于多類分類任務和訓練，通常通過用共享 softmax 函數替換各個激活函數來修改輸出層。每個神經元的輸出對應于相應類的估計概率。請注意，信號僅在一個方向上從輸入流向輸出，因此該架構是 FFNN 的示例。 作為案例研究，我們將使用銀行營銷數據集。這些數據與葡萄牙銀行機構的直接營銷活動有關。營銷活動基于電話。通常，不止一次聯系同一個客戶，以評估產品（銀行定期存款）是（是）還是不（否）訂閱。 目標是使用 MLP 來預測客戶是否會訂閱定期存款（變量 y），即二元分類問題。 ### 數據集描述 我想在此承認有兩個來源。這個數據集被用于 Moro 和其他人發表的一篇研究論文中：一種數據驅動的方法來預測銀行電話營銷的成功，決策支持系統，Elsevier，2014 年 6 月。后來，它被捐贈給了 UCI 機器學習庫，可以從[此鏈接](https://archive.ics.uci.edu/ml/datasets/bank+marketing)下載。 根據數據集描述，有四個數據集： * `bank-additional-full.csv`：這包括所有示例（41,188）和 20 個輸入，按日期排序（從 2008 年 5 月到 2010 年 11 月）。這些數據非常接近 Moro 和其他人分析的數據 * `bank-additional.csv`：這包括 10% 的例子（4119），從 1 和 20 個輸入中隨機選擇 * `bank-full.csv`：這包括按日期排序的所有示例和 17 個輸入（此數據集的較舊版本，輸入較少） * `bank.csv`：這包括 10% 的示例和 17 個輸入，從 3 中隨機選擇（此數據集的較舊版本，輸入較少） 數據集中有 21 個屬性。獨立變量可以進一步分類為與客戶相關的數據（屬性 1 到 7），與當前活動的最后一次聯系（屬性 8 到 11）相關。其他屬性（屬性 12 至 15）以及社會和經濟背景屬性（屬性 16 至 20）被分類。因變量由 y 指定，最后一個屬性（21）： | ID | 屬性 | 說明 | | --- | --- | --- | | 1 | `age` | 年齡數字。 | | 2 | `job` | 這是類別格式的職業類型，具有可能的值：`admin`，`blue-collar`，`entrepreneur`，`housemaid`，`management`，`retired`，`self-employed`，`services`，`student`，`technician`，`unemployed`和`unknown`。 | | 3 | `marital` | 這是類別格式的婚姻狀態，具有可能的值：`divorced`（或`widowed`），`married`，`single`和`unknown`。 | | 4 | `education` | 這是類別格式的教育背景，具有如下可能的值：`basic.4y`，`basic.6y`，`basic.9y`，`high.school`，`illiterate`，`professional.course`，`university.degree`和`unknown`。 | | 五 | `default` | 這是類別格式的信用，默認情況下可能包含：`no`，`yes`和`unknown`。 | | 6 | `housing` | 客戶是否有住房貸款？ | | 7 | `loan` | 類別格式的個人貸款，具有可能的值：`no`，`yes`和`unknown`。 | | 8 | `contact` | 這是類別格式的通信類型，具有可能的值：`cellular`或`telephone`。 | | 9 | `month` | 這是類別格式的一年中最后一個通話月份，具有可能的值：`jan`，`feb`，`mar`，... `nov`和`dec`。 | | 10 | `day_of_week` | 這是類別格式的一周中的最后一個通話日，具有可能的值：`mon`，`tue`，`wed`，`thu`和`fri`。 | | 11 | `duration` | 這是以秒為單位的最后一次通話持續時間（數值）。此屬性高度影響輸出目標（例如，如果`duration = 0`，則`y = no`）。然而，在通話之前不知道持續時間。另外，在通話結束后，`y`顯然是已知的。因此，此輸入僅應包括在基準目的中，如果打算采用現實的預測模型，則應將其丟棄。 | | 12 | `campaign` | 這是活動期間此客戶的通話數量。 | | 13 | `pdays` | 這是上一個廣告系列和客戶的上次通話之后經過的天數（數字 -999 表示之前未聯系過客戶）。 | | 14 | `previous` | 這是之前此廣告系列和此客戶的通話數量（數字）。 | | 15 | `poutcome` | 上一次營銷活動的結果（類別：`failure`，`nonexistent`和`success`）。 | | 16 | `emp.var.rate` | 這是就業變化率的季度指標（數字）。 | | 17 | `cons.price.idx` | 這是消費者價格指數的月度指標（數字）。 | | 18 | `cons.conf.idx` | 這是消費者信心指數的月度指標（數字）。 | | 19 | `euribor3m` | 這是 3 個月的 euribor 費率的每日指標（數字）。 | | 20 | `nr.employed` | 這是員工數的季度指標（數字）。 | | 21 | `y` | 表示客戶是否擁有定期存款，可能值是二元：`yes`和`no`。 | ### 預處理 您可以看到數據集尚未準備好直接輸入 MLP 或 DBN 分類器，因為該特征與數值和分類值混合在一起。此外，結果變量具有分類值。因此，我們需要將分類值轉換為數值，以便特征和結果變量以數字形式。下一步顯示了此過程。有關此預處理，請參閱`preprocessing_b.py`文件。 首先，我們必須加載預處理所需的所需包和庫： ```py import pandas as pd import numpy as np from sklearn import preprocessing ``` 然后從上述 URL 下載數據文件并將其放在方便的位置 - 比如說`input`： 然后，我們加載并解析數據集： ```py data = pd.read_csv('input/bank-additional-full.csv', sep = ";") ``` 接下來，我們將提取變量名稱： ```py var_names = data.columns.tolist() ``` 現在，基于表 1 中的數據集描述，我們將提取分類變量： ```py categs = ['job','marital','education','default','housing','loan','contact','month','day_of_week','duration','poutcome','y'] ``` 然后，我們將提取定量變量： ```py # Quantitative vars quantit = [i for i in var_names if i not in categs] ``` 然后讓我們得到分類變量的虛擬變量： ```py job = pd.get_dummies(data['job']) marital = pd.get_dummies(data['marital']) education = pd.get_dummies(data['education']) default = pd.get_dummies(data['default']) housing = pd.get_dummies(data['housing']) loan = pd.get_dummies(data['loan']) contact = pd.get_dummies(data['contact']) month = pd.get_dummies(data['month']) day = pd.get_dummies(data['day_of_week']) duration = pd.get_dummies(data['duration']) poutcome = pd.get_dummies(data['poutcome']) ``` 現在，是時候映射變量來預測： ```py dict_map = dict() y_map = {'yes':1,'no':0} dict_map['y'] = y_map data = data.replace(dict_map) label = data['y'] df_numerical = data[quantit] df_names = df_numerical .keys().tolist() ``` 一旦我們將分類變量轉換為數值變量，下一個任務就是正則化數值變量。因此，使用歸一化，我們將單個樣本縮放為具有單元規范。如果您計劃使用二次形式（如點積或任何其他內核）來量化任何樣本對的相似性，則此過程非常有用。該假設是在文本分類和聚類上下文中經常使用的[向量空間模型](https://en.wikipedia.org/wiki/Vector_space_model)的基礎。 那么，讓我們來衡量量化變量： ```py min_max_scaler = preprocessing.MinMaxScaler() x_scaled = min_max_scaler.fit_transform(df_numerical) df_temp = pd.DataFrame(x_scaled) df_temp.columns = df_names ``` 現在我們有（原始）數值變量的臨時數據幀，下一個任務是將所有數據幀組合在一起并生成正則化數據幀。我們將使用熊貓： ```py normalized_df = pd.concat([df_temp, job, marital, education, default, housing, loan, contact, month, day, poutcome, duration, label], axis=1) ``` 最后，我們需要將結果數據幀保存在 CSV 文件中，如下所示： ```py normalized_df.to_csv('bank_normalized.csv', index = False) ``` ### 用于客戶訂閱評估的 TensorFlow 中的 MLP 實現 對于這個例子，我們將使用我們在前面的例子中正則化的銀行營銷數據集。有幾個步驟可以遵循。首先，我們需要導入 TensorFlow，以及其他必要的包和模塊： ```py import tensorflow as tf import pandas as pd import numpy as np import os from sklearn.cross_validation import train_test_split # for random split of train/test ``` 現在，我們需要加載正則化的銀行營銷數據集，其中所有特征和標簽都是數字。為此，我們使用 pandas 庫中的`read_csv()`方法： ```py FILE_PATH = 'bank_normalized.csv' # Path to .csv dataset raw_data = pd.read_csv(FILE_PATH) # Open raw .csv print("Raw data loaded successfully...\n") ``` 以下是上述代碼的輸出： ```py >>> Raw data loaded successfully... ``` 如前一節所述，調整 DNN 的超參數并不簡單。但是，它通常取決于您正在處理的數據集。對于某些數據集，可能的解決方法是根據與數據集相關的統計信息設置這些值，例如，訓練實例的數量，輸入大小和類的數量。 DNN 不適用于小型和低維數據集。在這些情況下，更好的選擇是使用線性模型。首先，讓我們放置一個指向標簽列本身的指針，計算實例數和類數，并定義訓練/測試分流比，如下所示： ```py Y_LABEL = 'y' # Name of the variable to be predicted KEYS = [i for i in raw_data.keys().tolist() if i != Y_LABEL]# Name of predictors N_INSTANCES = raw_data.shape[0] # Number of instances N_INPUT = raw_data.shape[1] - 1 # Input size N_CLASSES = raw_data[Y_LABEL].unique().shape[0] # Number of classes TEST_SIZE = 0.25 # Test set size (% of dataset) TRAIN_SIZE = int(N_INSTANCES * (1 - TEST_SIZE)) # Train size ``` 現在，讓我們看一下我們將用于訓練 MLP 模型的數據集的統計數據： ```py print("Variables loaded successfully...\n") print("Number of predictors \t%s" %(N_INPUT)) print("Number of classes \t%s" %(N_CLASSES)) print("Number of instances \t%s" %(N_INSTANCES)) print("\n") ``` 以下是上述代碼的輸出： ```py >>> Variables loaded successfully... Number of predictors 1606 Number of classes 2 Number of instances 41188 ``` 下一個任務是定義其他參數，例如學習率，訓練周期，批量大小和權重的標準偏差。通常，較低的訓練率會幫助您的 DNN 學習更慢，但需要集中精力。請注意，我們需要定義更多參數，例如隱藏層數和激活函數。 ```py LEARNING_RATE = 0.001 # learning rate TRAINING_EPOCHS = 1000 # number of training epoch for the forward pass BATCH_SIZE = 100 # batch size to be used during training DISPLAY_STEP = 20 # print the error etc. at each 20 step HIDDEN_SIZE = 256 # number of neurons in each hidden layer # We use tanh as the activation function, but you can try using ReLU as well ACTIVATION_FUNCTION_OUT = tf.nn.tanh STDDEV = 0.1 # Standard Deviations RANDOM_STATE = 100 ``` 前面的初始化是基于反復試驗設置的 。因此，根據您的用例和數據類型，明智地設置它們，但我們將在本章后面提供一些指導。此外，對于前面的代碼，`RANDOM_STATE`用于表示訓練的隨機狀態和測試分割。首先，我們將原始特征和標簽分開： ```py data = raw_data[KEYS].get_values() # X data labels = raw_data[Y_LABEL].get_values() # y data ``` 現在我們有標簽，他們必須編碼： ```py labels_ = np.zeros((N_INSTANCES, N_CLASSES)) labels_[np.arange(N_INSTANCES), labels] = 1 ``` 最后，我們必須拆分訓練和測試集。如前所述，我們將保留 75% 的訓練輸入，剩下的 25% 用于測試集： ```py data_train, data_test, labels_train, labels_test = train_test_split(data,labels_,test_size = TEST_SIZE,random_state = RANDOM_STATE) print("Data loaded and splitted successfully...\n") ``` 以下是上述代碼的輸出： ```py >>> Data loaded and splitted successfully ``` 由于這是一個監督分類問題，我們應該有特征和標簽的占位符： 如前所述，MLP 由一個輸入層，幾個隱藏層和一個稱為輸出層的最終 LTU 層組成。對于這個例子，我將把訓練與四個隱藏層結合起來。因此，我們將分類器稱為深度前饋 MLP。請注意，我們還需要在每個層中使用權重（輸入層除外），以及每個層中的偏差（輸出層除外）。通常，每個隱藏層包括偏置神經元，并且作為從一個隱藏層到另一個隱藏層的完全連接的二分圖（前饋）完全連接到下一層。那么，讓我們定義隱藏層的大小： ```py n_input = N_INPUT # input n labels n_hidden_1 = HIDDEN_SIZE # 1st layer n_hidden_2 = HIDDEN_SIZE # 2nd layer n_hidden_3 = HIDDEN_SIZE # 3rd layer n_hidden_4 = HIDDEN_SIZE # 4th layer n_classes = N_CLASSES # output m classes ``` 由于這是一個監督分類問題，我們應該有特征和標簽的占位符： ```py # input shape is None * number of input X = tf.placeholder(tf.float32, [None, n_input]) ``` 占位符的第一個維度是`None`，這意味著我們可以有任意數量的行。第二個維度固定在多個特征上，這意味著每行需要具有該列數量的特征。 ```py # label shape is None * number of classes y = tf.placeholder(tf.float32, [None, n_classes]) ``` 另外，我們需要另一個占位符用于丟棄，這是通過僅以某種可能性保持神經元活動（例如`p < 1.0`，或者將其設置為零來實現）來實現的。請注意，這也是要調整的超參數和訓練時間，而不是測試時間： ```py dropout_keep_prob = tf.placeholder(tf.float32) ``` 使用此處給出的縮放，可以將相同的網絡用于訓練（使用`dropout_keep_prob < 1.0`）和評估（使用`dropout_keep_prob == 1.0`）。現在，我們可以定義一個實現 MLP 分類器的方法。為此，我們將提供四個參數，如輸入，權重，偏置和丟棄概率，如下所示： ```py def DeepMLPClassifier(_X, _weights, _biases, dropout_keep_prob): layer1 = tf.nn.dropout(tf.nn.tanh(tf.add(tf.matmul(_X, _weights['h1']), _biases['b1'])), dropout_keep_prob) layer2 = tf.nn.dropout(tf.nn.tanh(tf.add(tf.matmul(layer1, _weights['h2']), _biases['b2'])), dropout_keep_prob) layer3 = tf.nn.dropout(tf.nn.tanh(tf.add(tf.matmul(layer2, _weights['h3']), _biases['b3'])), dropout_keep_prob) layer4 = tf.nn.dropout(tf.nn.tanh(tf.add(tf.matmul(layer3, _weights['h4']), _biases['b4'])), dropout_keep_prob) out = ACTIVATION_FUNCTION_OUT(tf.add(tf.matmul(layer4, _weights['out']), _biases['out'])) return out ``` 上述方法的返回值是激活函數的輸出。前面的方法是一個存根實現，它沒有告訴任何關于權重和偏置的具體內容，所以在我們開始訓練之前，我們應該定義它們： ```py weights = { 'w1': tf.Variable(tf.random_normal([n_input, n_hidden_1],stddev=STDDEV)), 'w2': tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2],stddev=STDDEV)), 'w3': tf.Variable(tf.random_normal([n_hidden_2, n_hidden_3],stddev=STDDEV)), 'w4': tf.Variable(tf.random_normal([n_hidden_3, n_hidden_4],stddev=STDDEV)), 'out': tf.Variable(tf.random_normal([n_hidden_4, n_classes],stddev=STDDEV)), } biases = { 'b1': tf.Variable(tf.random_normal([n_hidden_1])), 'b2': tf.Variable(tf.random_normal([n_hidden_2])), 'b3': tf.Variable(tf.random_normal([n_hidden_3])), 'b4': tf.Variable(tf.random_normal([n_hidden_4])), 'out': tf.Variable(tf.random_normal([n_classes])) } ``` 現在我們可以使用真實參數（輸入層，權重，偏置和退出）調用前面的 MLP 實現，保持概率如下： ```py pred = DeepMLPClassifier(X, weights, biases, dropout_keep_prob) ``` 我們建立了 MLP 模型，是時候訓練網絡了。首先，我們需要定義成本操作，然后我們將使用 Adam 優化器，它將慢慢學習并嘗試盡可能減少訓練損失： ```py cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=pred, labels=y)) # Optimization op (backprop) optimizer = tf.train.AdamOptimizer(learning_rate = LEARNING_RATE).minimize(cost_op) ``` 接下來，我們需要定義用于計算分類準確率的其他參數： ```py correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) print("Deep MLP networks has been built successfully...") print("Starting training...") ``` 之后，我們需要在啟動 TensorFlow 會話之前初始化所有變量和占位符： ```py init_op = tf.global_variables_initializer() ``` 現在，我們非常接近開始訓練，但在此之前，最后一步是創建 TensorFlow 會話并按如下方式啟動它： ```py sess = tf.Session() sess.run(init_op) ``` 最后，我們準備開始在訓練集上訓練我們的 MLP。我們遍歷所有批次并使用批量數據擬合以計算平均訓練成本。然而，顯示每個周期的訓練成本和準確率會很棒： ```py for epoch in range(TRAINING_EPOCHS): avg_cost = 0.0 total_batch = int(data_train.shape[0] / BATCH_SIZE) # Loop over all batches for i in range(total_batch): randidx = np.random.randint(int(TRAIN_SIZE), size = BATCH_SIZE) batch_xs = data_train[randidx, :] batch_ys = labels_train[randidx, :] # Fit using batched data sess.run(optimizer, feed_dict={X: batch_xs, y: batch_ys, dropout_keep_prob: 0.9}) # Calculate average cost avg_cost += sess.run(cost, feed_dict={X: batch_xs, y: batch_ys, dropout_keep_prob:1.})/total_batch # Display progress if epoch % DISPLAY_STEP == 0: print("Epoch: %3d/%3d cost: %.9f" % (epoch, TRAINING_EPOCHS, avg_cost)) train_acc = sess.run(accuracy, feed_dict={X: batch_xs, y: batch_ys, dropout_keep_prob:1.}) print("Training accuracy: %.3f" % (train_acc)) print("Your MLP model has been trained successfully.") ``` 以下是上述代碼的輸出： ```py >>> Starting training... Epoch: 0/1000 cost: 0.356494816 Training accuracy: 0.920 … Epoch: 180/1000 cost: 0.350044933 Training accuracy: 0.860 …. Epoch: 980/1000 cost: 0.358226758 Training accuracy: 0.910 ``` 干得好，我們的 MLP 模型已經成功訓練！現在，如果我們以圖形方式看到成本和準確率怎么辦？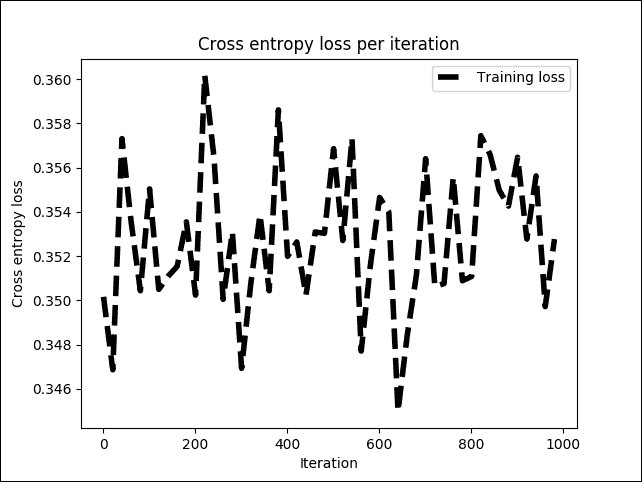我們來試試吧： ```py # Plot loss over time plt.subplot(221) plt.plot(i_data, cost_list, 'k--', label='Training loss', linewidth=1.0) plt.title('Cross entropy loss per iteration') plt.xlabel('Iteration') plt.ylabel('Cross entropy loss') plt.legend(loc='upper right') plt.grid(True) ``` 以下是上述代碼的輸出 ： ```py >>> ```  圖 11：訓練階段每次迭代的交叉熵損失 上圖顯示交叉熵損失在 0.34 和 0.36 之間或多或少穩定，但波動很小。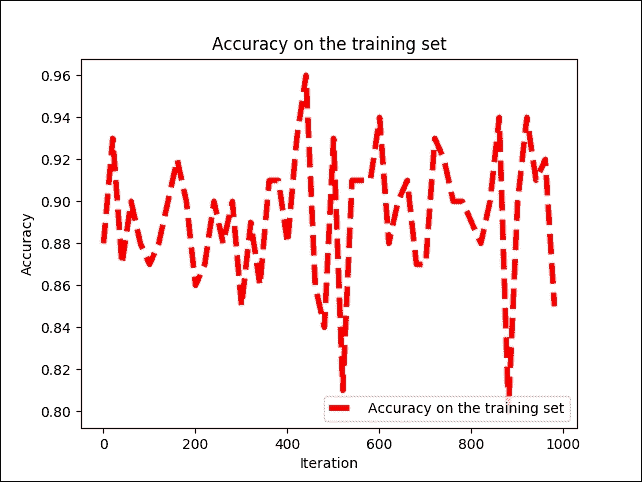現在，讓我們看看這對整體訓練準確率有何影響： ```py # Plot train and test accuracy plt.subplot(222) plt.plot(i_data, acc_list, 'r--', label='Accuracy on the training set', linewidth=1.0) plt.title('Accuracy on the training set') plt.xlabel('Iteration') plt.ylabel('Accuracy') plt.legend(loc='upper right') plt.grid(True) plt.show() ``` 以下是前面代碼的輸出： ```py >>> ```  圖 12：每次迭代時訓練集的準確率 我們可以看到訓練準確率在 79% 和 96% 之間波動，但不會均勻地增加或減少。解決此問題的一種可能方法是添加更多隱藏層并使用不同的優化器，例如本章前面討論的梯度下降。我們將丟棄概率提高到 100%，即 1.0。原因是也有相同的網絡用于測試： ```py print("Evaluating MLP on the test set...") test_acc = sess.run(accuracy, feed_dict={X: data_test, y: labels_test, dropout_keep_prob:1.}) print ("Prediction/classification accuracy: %.3f" % (test_acc)) ``` 以下是上述代碼的輸出： ```py >>> Evaluating MLP on the test set... Prediction/classification accuracy: 0.889 Session closed! ``` 因此，分類準確率約為 89%。一點也不差！現在，如果需要更高的精度，我們可以使用稱為深度信任網絡（DBN）的另一種 DNN 架構，可以以有監督或無監督的方式進行訓練。 這是在其應用中作為分類器觀察 DBN 的最簡單方法。如果我們有一個 DBN 分類器，那么預訓練方法是以類似于自編碼器的無監督方式完成的，這將在第 5 章中描述，優化 TensorFlow 自編碼器，分類器以受監督的方式訓練（微調），就像 MLP 中的那樣。 ## 深度信念網絡（DBNs） 為了克服 MLP 中的過擬合問題，我們建立了一個 DBN，進行無監督的預訓練，為輸入獲得一組不錯的特征表示，然后對訓練集進行微調以獲得預測。網絡。 雖然 MLP 的權重是隨機初始化的，但 DBN 使用貪婪的逐層預訓練算法通過概率生成模型初始化網絡權重。這些模型由可見層和多層隨機潛在變量組成，這些變量稱為隱藏單元或特征檢測器。 堆疊 DBN 中的 RBM，形成無向概率圖模型，類似于馬爾可夫隨機場（MRF）：兩層由可見神經元和隱藏神經元組成。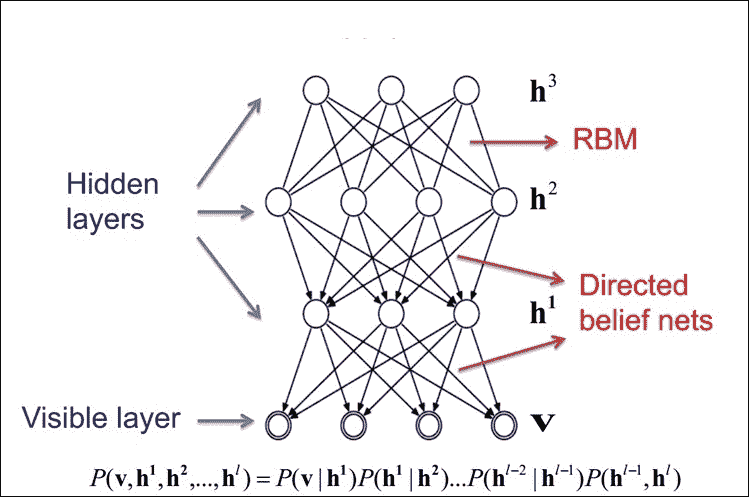 堆疊 RBM 中的頂部兩層在它們之間具有無向的對稱連接并形成關聯存儲器，而較低層從上面的層接收自上而下的定向連接：  圖 13：RBM 作為構建塊的 DBN 的高級視圖 頂部兩層在它們之間具有無向的對稱連接并形成關聯存儲器，而較低層從前面的層接收自上而下的定向連接。幾個 RBM 一個接一個地堆疊以形成 DBN。 ### 受限玻爾茲曼機（RBMs） RBM 是無向概率圖模型，稱為馬爾科夫隨機場。它由兩層組成。第一層由可見神經元組成，第二層由隱藏神經元組成。圖 14 顯示了簡單 RBM 的結構。可見單元接受輸入，隱藏單元是非線性特征檢測器。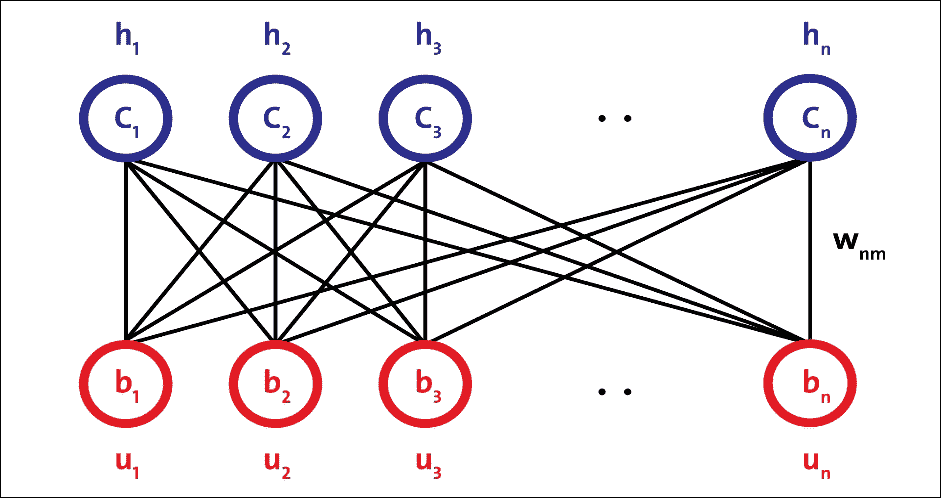每個可見神經元都連接到所有隱藏的神經元，但同一層中的神經元之間沒有內部連接：  圖 14：簡單 RBM 的結構 圖 14 中的 RBM 由`m`個可見單元組成，`V = (v[1] ... v[m])`和`n`個隱藏單元，`H = (h[1] ... h[n])`。可見單元接受 0 到 1 之間的值，隱藏單元的生成值介于 0 和 1 之間。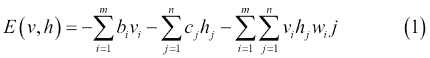模型的聯合概率是由以下等式給出的能量函數：  在前面的等式中，`i = 1 ... m`，`j = 1 ... n`，`bi`和`cj`分別是可見和隱藏單元的偏差，并且`w[ij]`是`v[i]`和`h[j]`之間的權重。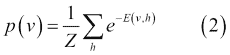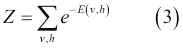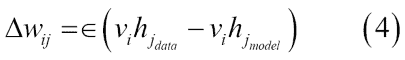模型分配給可見向量`v`的概率由下式給出：  在第二個等式中，`Z`是分區函數，定義如下：  權重的學習可以通過以下等式獲得：  在等式 4 中，學習率由`eps`定義。通常，較小的`eps`值可確保訓練更加密集。但是，如果您希望網絡快速學習，可以將此值設置得更高。 由于同一層中的單元之間沒有連接，因此很容易計算第一項。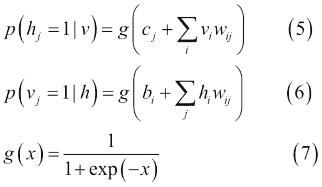`p(h | v)`和`p(v | h)`的條件分布是階乘的，并且由以下等式中的邏輯函數給出：  因此，樣本`v[i] h[j]`是無偏的。然而，計算第二項的對數似然的計算成本是指數級的。雖然有可能得到第二項的無偏樣本，但使用馬爾可夫鏈蒙特卡羅（MCMC）的吉布斯采樣，這個過程也不具有成本效益。相反，RBM 使用稱為對比發散的有效近似方法。 通常，MCMC 需要許多采樣步驟才能達到靜止的收斂。運行吉布斯采樣幾步（通常是一步）足以訓練一個模型，這稱為對比分歧學習。對比分歧的第一步是用訓練向量初始化可見單元。 下一步是使用等式 5 計算所有隱藏單元，同時使用可見單元，然后使用等式 4 從隱藏單元重建可見單元。最后，隱藏單元用重建的可見單元更新。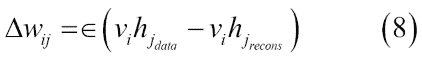因此，代替方程式 4，我們最終得到以下的權重學習模型：  簡而言之，該過程試圖減少輸入數據和重建數據之間的重建誤差。算法收斂需要多次參數更新迭代。迭代稱為周期。輸入數據被分成小批量，并且在每個小批量之后更新參數，具有參數的平均值。 最后，如前所述，RBM 最大化可見單元`p(v)`的概率，其由模式和整體訓練數據定義。它相當于最小化模型分布和經驗數據分布之間的 [KL 散度](https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence)。 對比分歧只是這個目標函數的粗略近似，但它在實踐中非常有效。雖然方便，但重建誤差實際上是衡量學習進度的一個非常差的指標。考慮到這些方面，RBM 需要一些時間來收斂，但是如果你看到重建是不錯的，那么你的算法效果很好。 ### 構建一個簡單的 DBN 單個隱藏層 RBM 無法從輸入數據中提取所有特征，因為它無法對變量之間的關系進行建模。因此，一層接一個地使用多層 RBM 來提取非線性特征。在 DBN 中，首先使用輸入數據訓練 RBM，并且隱藏層以貪婪學習方法表示學習的特征。 第一 RBM 的這些學習特征用作第二 RBM 的輸入，作為 DBN 中的另一層，如圖 15 所示。類似地，第二層的學習特征用作另一層的輸入。 這樣，DBN 可以從輸入數據中提取深度和非線性特征。最后一個 RBM 的隱藏層代表整個網絡的學習特征。前面針對所有 RBM 層描述的學習特征的過程稱為預訓練。 ### 無監督的預訓練 假設您要處理復雜任務，您沒有多少標記的訓練數據。很難找到合適的 DNN 實現或架構來進行訓練并用于預測分析。然而，如果您有大量未標記的訓練數據，您可以嘗試逐層訓練層，從最低層開始，然后使用無監督的特征檢測器算法向上移動。這就是 RBM（圖 15）或自編碼器（圖 16）的工作原理。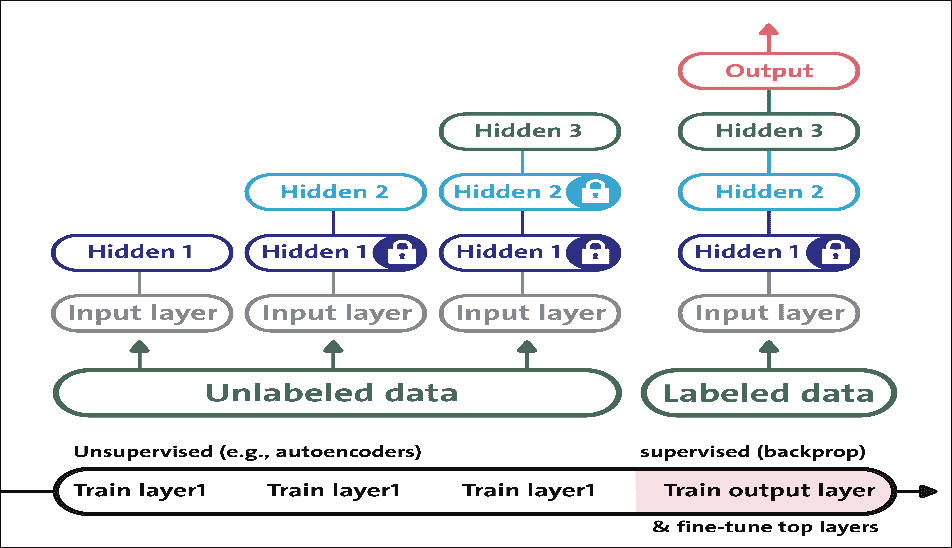  圖 15：使用自編碼器在 DBN 中進行無監督的預訓練 當您有一個復雜的任務需要解決時，無監督的預訓練仍然是一個不錯的選擇，沒有類似的模型可以重復使用，并且標記很少的訓練數據，但是大量未標記的訓練數據。目前的趨勢是使用自編碼器而不是 RBM；但是，對于下一節中的示例，RBM 將用于簡化。讀者也可以嘗試使用自編碼器而不是 RBM。 預訓練是一種無監督的學習過程。在預訓練之后，通過在最后一個 RBM 層的頂部添加標記層來執行網絡的微調。此步驟是受監督的學習過程。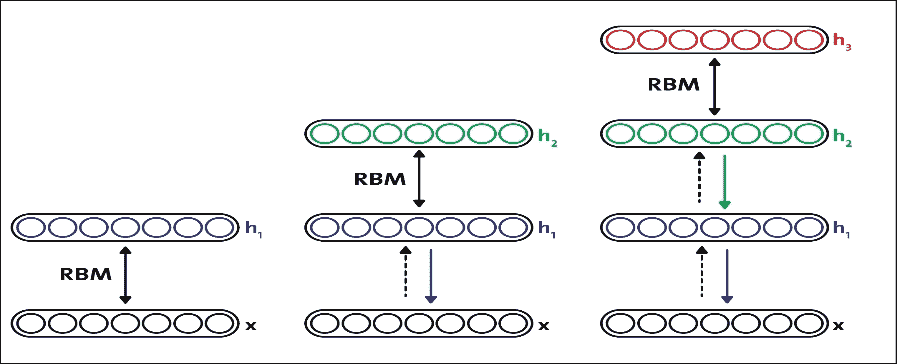無監督的預訓練步驟嘗試查找網絡權重：  圖 16：通過構建具有 RBM 棧的簡單 DBN 在 DBN 中進行無監督預訓練 ### 監督的微調 在監督學習階段（也稱為監督微調）中，不是隨機初始化網絡權重，而是使用在預訓練步驟中計算的權重來初始化它們。這樣，當使用監督梯度下降時，DBN 可以避免收斂到局部最小值。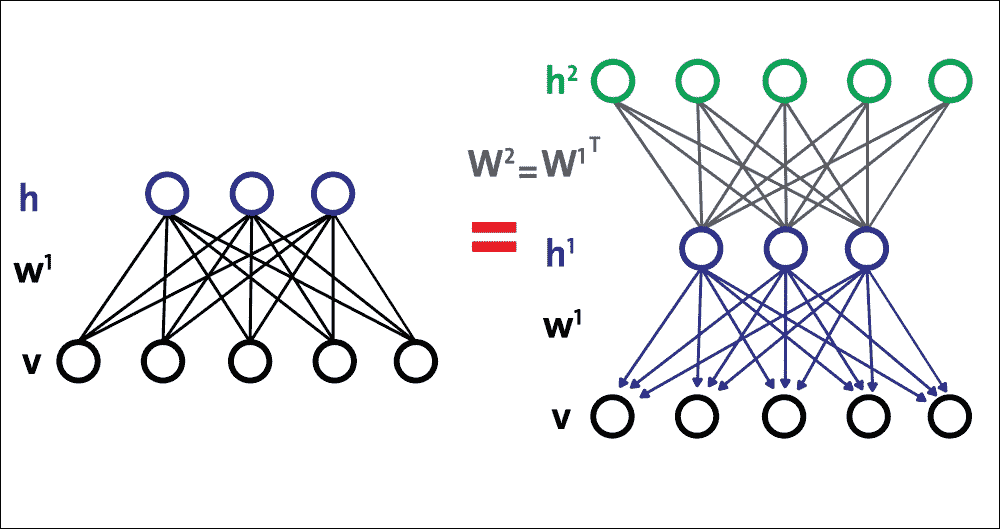 如前所述，使用 RBM 棧，DBN 可以構造如下： * 使用參數`W[1]`訓練底部 RBM（第一個 RBM） * 將第二層權重初始化為`W[2] = W[1]^T`，這可確保 DBN 至少與我們的基礎 RBM 一樣好 因此，將這些步驟放在一起，圖 17 顯示了由三個 RBM 組成的簡單 DBN 的構造：  圖 17：使用多個 RBM 構建簡單的 DBN 現在，當調整 DBN 以獲得更好的預測準確率時，我們應該調整幾個超參數，以便 DBN 通過解開和改進`W[2]`來擬合訓練數據。綜上所述，我們有了創建基于 DBN 的分類器或回歸器的概念工作流程。 現在我們已經有足夠的理論背景來介紹如何使用幾個 RBM 構建 DBN，現在是時候將我們的理論應用于實踐中了。在下一節中，我們將了解如何開發用于預測分析的監督 DBN 分類器。 ## 用于客戶訂閱評估的 TensorFlow 中的 DBN 實現 在銀行營銷數據集的前一個示例中，我們使用 MLP 觀察到大約 89% 的分類準確率。我們還將原始數據集標準化，然后將其提供給 MLP。在本節中，我們將了解如何為基于 DBN 的預測模型使用相同的數據集。 我們將使用 Md.Rezaul Karim 最近出版的書籍 Predictive Analytics with TensorFlow 的 DBN 實現，可以從 [GitHub](https://github.com/PacktPublishing/Predictive-Analytics-with-TensorFlow/tree/master/Chapter07/DBN) 下載。 前面提到的實現是基于 RBM 的簡單，干凈，快速的 DBN 實現，并且基于 NumPy 和 TensorFlow 庫，以便利用 GPU 計算。該庫基于以下兩篇研究論文實現： * Geoffrey E. Hinton，Simon Osindero 和 Yee-Whye Teh 的深度信念網快速學習算法。 Neural Computation 18.7（2006）：1527-1554。 * 訓練受限制的玻爾茲曼機：簡介，Asja Fischer 和 Christian Igel。模式識別 47.1（2014）：25-39。 我們將看到如何以無監督的方式訓練 RBM，然后我們將以有監督的方式訓練網絡。簡而言之，有幾個步驟需要遵循。主分類器是`classification_demo.py`。 ### 提示 雖然在以監督和無監督的方式訓練 DBN 時數據集不是那么大或高維度，但是在訓練時間中會有如此多的計算，這需要巨大的資源。然而，RBM 需要大量時間來收斂。因此，我建議讀者在 GPU 上進行訓練，至少擁有 32 GB 的 RAM 和一個 Corei7 處理器。 我們將從加載所需的模塊和庫開始： ```py import numpy as np import pandas as pd from sklearn.datasets import load_digits from sklearn.model_selection import train_test_split from sklearn.metrics.classification import accuracy_score from sklearn.metrics import precision_recall_fscore_support from sklearn.metrics import confusion_matrix import itertools from tf_models import SupervisedDBNClassification import matplotlib.pyplot as plt ``` 然后，我們加載前一個 MLP 示例中使??用的已經正則化的數據集： ```py FILE_PATH = '../input/bank_normalized.csv' raw_data = pd.read_csv(FILE_PATH) ``` 在前面的代碼中，我們使用了 pandas `read_csv()`方法并創建了一個`DataFrame`。現在，下一個任務是按如下方式擴展特征和標簽： ```py Y_LABEL = 'y' KEYS = [i for i in raw_data.keys().tolist() if i != Y_LABEL] X = raw_data[KEYS].get_values() Y = raw_data[Y_LABEL].get_values() class_names = list(raw_data.columns.values) print(class_names) ``` 在前面的行中，我們已經分離了特征和標簽。這些特征存儲在`X`中，標簽位于`Y`中。接下來的任務是將它們分成訓練（75%）和測試集（25%），如下所示： ```py X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.25, random_state=100) ``` 現在我們已經有了訓練和測試集，我們可以直接進入 DBN 訓練步驟。但是，首先我們需要實例化 DBN。我們將以受監督的方式進行分類，但我們需要為此 DNN 架構提供超參數： ```py classifier = SupervisedDBNClassification(hidden_layers_structure=[64, 64],learning_rate_rbm=0.05,learning_rate=0.01,n_epochs_rbm=10,n_iter_backprop=100,batch_size=32,activation_function='relu',dropout_p=0.2) ``` 在前面的代碼段中，`n_epochs_rbm`是預訓練（無監督）和`n_iter_backprop`用于監督微調的周期數。盡管如此，我們已經為這兩個階段定義了兩個單獨的學習率，分別使用`learning_rate_rbm`和`learning_rate`。 不過，我們將在本節后面描述`SupervisedDBNClassification`的這個類實現。 該庫具有支持 sigmoid，ReLU 和 tanh 激活函數的實現。此外，它利用 l2 正則化來避免過擬合。我們將按如下方式進行實際擬合： ```py classifier.fit(X_train, Y_train) ``` 如果一切順利，你應該在控制臺上觀察到以下進展： ```py [START] Pre-training step: >> Epoch 1 finished RBM Reconstruction error 1.681226 …. >> Epoch 3 finished RBM Reconstruction error 4.926415 >> Epoch 5 finished RBM Reconstruction error 7.185334 … >> Epoch 7 finished RBM Reconstruction error 37.734962 >> Epoch 8 finished RBM Reconstruction error 467.182892 …. >> Epoch 10 finished RBM Reconstruction error 938.583801 [END] Pre-training step [START] Fine tuning step: >> Epoch 0 finished ANN training loss 0.316619 >> Epoch 1 finished ANN training loss 0.311203 >> Epoch 2 finished ANN training loss 0.308707 …. >> Epoch 98 finished ANN training loss 0.288299 >> Epoch 99 finished ANN training loss 0.288900 ``` 由于 RBM 的權重是隨機初始化的，因此重建和原始輸入之間的差異通常很大。 從技術上講，我們可以將重建誤差視為重建值與輸入值之間的差異。然后，在迭代學習過程中，將該誤差反向傳播 RBM 的權重幾次，直到達到最小誤差。 然而，在我們的情況下，重建達到 938，這不是那么大（即，不是無限），所以我們仍然可以期望良好的準確率。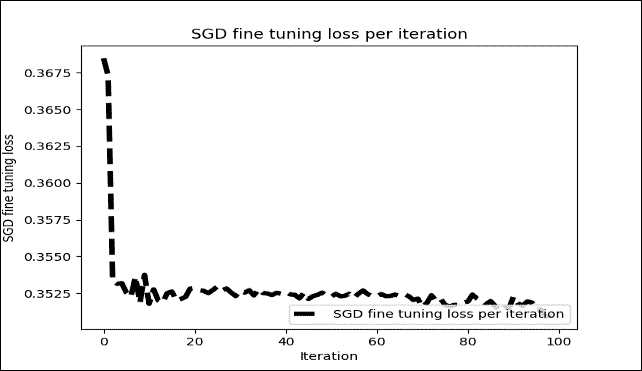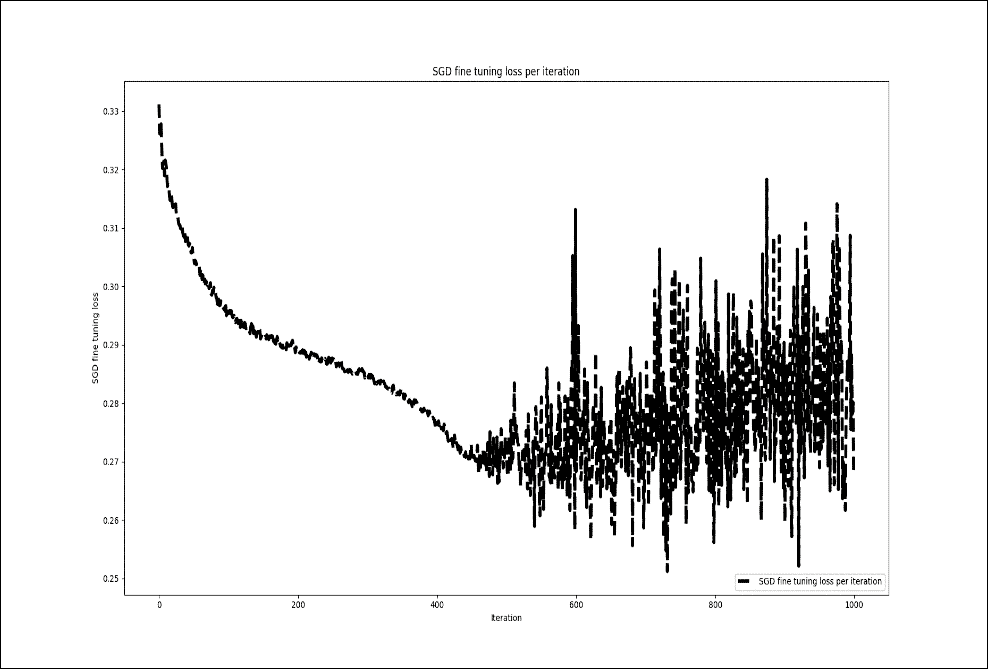無論如何，經過 100 次迭代后，顯示每個周期訓練光澤的微調圖如下：  圖 18：每次迭代的 SGD 微調損失（僅 100 次迭代） 然而，當我重復前面的訓練并微調 1000 個周期時，我沒有看到訓練損失有任何顯著改善：  圖 19：每次迭代的 SGD 微調損失（1000 次迭代） 這是監督的 DBN 分類器的實現。此類為分類問題實現 DBN。它將網絡輸出轉換為原始標簽。在對標簽映射執行索引之后，它還需要網絡參數并返回列表。 然后，該類預測給定數據中每個樣本的類的概率分布，并返回字典列表（每個樣本一個）。最后，它附加了 softmax 線性分類器作為輸出層： ```py class SupervisedDBNClassification(TensorFlowAbstractSupervisedDBN, ClassifierMixin): def _build_model(self, weights=None): super(SupervisedDBNClassification, self)._build_model(weights) self.output = tf.nn.softmax(self.y) self.cost_function = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=self.y, labels=self.y_)) self.train_step = self.optimizer.minimize(self.cost_function) @classmethod def _get_param_names(cls): return super(SupervisedDBNClassification, cls)._get_param_names() + ['label_to_idx_map', 'idx_to_label_map'] @classmethod def from_dict(cls, dct_to_load): label_to_idx_map = dct_to_load.pop('label_to_idx_map') idx_to_label_map = dct_to_load.pop('idx_to_label_map') instance = super(SupervisedDBNClassification, cls).from_dict(dct_to_load) setattr(instance, 'label_to_idx_map', label_to_idx_map) setattr(instance, 'idx_to_label_map', idx_to_label_map) return instance def _transform_labels_to_network_format(self, labels): """ Converts network output to original labels. :param indexes: array-like, shape = (n_samples, ) :return: """ new_labels, label_to_idx_map, idx_to_label_map = to_categorical(labels, self.num_classes) self.label_to_idx_map = label_to_idx_map self.idx_to_label_map = idx_to_label_map return new_labels def _transform_network_format_to_labels(self, indexes): return list(map(lambda idx: self.idx_to_label_map[idx], indexes)) def predict(self, X): probs = self.predict_proba(X) indexes = np.argmax(probs, axis=1) return self._transform_network_format_to_labels(indexes) def predict_proba(self, X): """ Predicts probability distribution of classes for each sample in the given data. :param X: array-like, shape = (n_samples, n_features) :return: """ return super(SupervisedDBNClassification, self)._compute_output_units_matrix(X) def predict_proba_dict(self, X): """ Predicts probability distribution of classes for each sample in the given data. Returns a list of dictionaries, one per sample. Each dict contains {label_1: prob_1, ..., label_j: prob_j} :param X: array-like, shape = (n_samples, n_features) :return: """ if len(X.shape) == 1: # It is a single sample X = np.expand_dims(X, 0) predicted_probs = self.predict_proba(X) result = [] num_of_data, num_of_labels = predicted_probs.shape for i in range(num_of_data): # key : label # value : predicted probability dict_prob = {} for j in range(num_of_labels): dict_prob[self.idx_to_label_map[j]] = predicted_probs[i][j] result.append(dict_prob) return result def _determine_num_output_neurons(self, labels): return len(np.unique(labels)) ``` 正如我們在前面的例子和運行部分中提到的那樣，微調神經網絡的參數是一個棘手的過程。有很多不同的方法，但我的知識并沒有一刀切的方法。然而，通過前面的組合，我收到了更好的分類結果。另一個要選擇的重要參數是學習率。根據您的模型調整學習率是一種可以采取的方法，以減少訓練時間，同時避免局部最小化。在這里，我想討論一些能夠幫助我提高預測準確率的技巧，不僅適用于此應用，也適用于其他應用。 現在我們已經建立了模型，現在是評估其表現的時候了。為了評估分類準確率，我們將使用幾個表現指標，如`precision`，`recall`和`f1 score`。此外，我們將繪制混淆矩陣，以觀察與真實標簽相對應的預測標簽。首先，讓我們計算預測精度如下： ```py Y_pred = classifier.predict(X_test) print('Accuracy: %f' % accuracy_score(Y_test, Y_pred)) ``` 接下來，我們需要計算分類的`precision`，`recall`和`f1 score`： ```py p, r, f, s = precision_recall_fscore_support(Y_test, Y_pred, average='weighted') print('Precision:', p) print('Recall:', r) print('F1-score:', f) ``` 以下是上述代碼的輸出： ```py >>> Accuracy: 0.900554 Precision: 0.8824140209830381 Recall: 0.9005535592891133 F1-score: 0.8767190584424599 ``` 太棒了！使用我們的 DBN 實現，我們解決了與使用 MLP 相同的分類問題。盡管如此，與 MLP 相比，我們設法獲得了稍微更好的準確率。 現在，如果要解決回歸問題，要預測的標簽是連續的，則必須使用`SupervisedDBNRegression()`函數進行此實現。 DBN 文件夾中的回歸腳本（即`regression_demo.py`）也可用于執行回歸操作。 但是，使用專門為回歸 y 準備的另一個數據集將是更好的主意。您需要做的就是準備數據集，以便基于 TensorFlow 的 DBN 可以使用它。因此，為了最小化演示，我使用房價：高級回歸技術數據集來預測房價。 # 調整超參數和高級 FFNN 神經網絡的靈活性也是它們的主要缺點之一：有很多超參數可以調整。即使在簡單的 MLP 中，您也可以更改層數，每層神經元的數量以及每層中使用的激活函數的類型。您還可以更改權重初始化邏輯，退出保持概率等。 另外，FFNN 中的一些常見問題，例如梯度消失問題，以及選擇最合適的激活函數，學習率和優化器，是最重要的。 ## 調整 FFNN 超參數 超參數是不在估計器中直接學習的參數。有可能并建議您在超參數空間中搜索[最佳交叉驗證](http://scikit-learn.org/stable/modules/cross_validation.html#cross-validation)得分。在構造估計器時提供的任何參數可以以這種方式優化。現在，問題是：您如何知道超參數的哪種組合最適合您的任務？當然，您可以使用網格搜索和交叉驗證來為線性機器學習模型找到正確的超參數。 但是，對于 DNN，有許多超參數可供調整。由于在大型數據集上訓練神經網絡需要花費大量時間，因此您只能在合理的時間內探索超參數空間的一小部分。以下是一些可以遵循的見解。 此外，當然，正如我所說，您可以使用網格搜索或隨機搜索，通過交叉驗證，為線性機器學習模型找到正確的超參數。我們將在本節后面看到一些可能的詳盡和隨機網格搜索和交叉驗證方法。 ### 隱藏層數 對于許多問題，你可以從一個或兩個隱藏層開始，這個設置可以很好地使用兩個隱藏層，具有相同的神經元總數（見下文以了解一些神經元），訓練時間大致相同。現在讓我們看一些關于設置隱藏層數的樸素估計： * 0：僅能表示線性可分離函數或決策 * 1：可以近似包含從一個有限空間到另一個有限空間的連續映射的任何函數 * 2：可以用任意精度表示任意決策邊界，具有合理的激活函數，并且可以近似任何平滑映射到任何精度 但是，對于更復雜的問題，您可以逐漸增加隱藏層的數量，直到您開始過擬合訓練集。非常復雜的任務，例如大圖像分類或語音識別，通常需要具有數十層的網絡，并且它們需要大量的訓練數據。 不過，您可以嘗試逐漸增加神經元的數量，直到網絡開始過擬合。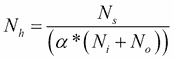這意味著不會導致過擬合的隱藏神經元數量的上限是：  在上面的等式中： `N[i]`為輸入神經元的數量 `N[o]`為輸出神經元的數量 `N[s]`為訓練數據集中的樣本數 `α`為任意比例因子，通常為 2-10。 請注意，上述等式不是來自任何研究，而是來自我的個人工作經驗。但是，對于自動程序，您將以 2 的`α`值開始，即訓練數據的自由度是模型的兩倍，如果訓練數據的誤差明顯小于 10，則可以達到 10。用于交叉驗證數據集。 ### 每個隱藏層的神經元數量 顯然，輸入和輸出層中神經元的數量取決于您的任務所需的輸入和輸出類型。例如，如果您的數據集的形狀為`28x28`，則它應該具有大小為 784 的輸入神經元，并且輸出神經元應該等于要預測的類的數量。 我們將在下一個例子中看到它如何在實踐中工作，使用 MLP，其中將有四個具有 256 個神經元的隱藏層（只有一個超參數可以調整，而不是每層一個）。就像層數一樣，您可以嘗試逐漸增加神經元的數量，直到網絡開始過擬合。 有一些經驗導出的經驗法則，其中最常用的是：“隱藏層的最佳大小通常在輸入的大小和輸出層的大小之間。” 總之，對于大多數問題，通過僅使用兩個規則設置隱藏層配置，您可能可以獲得不錯的表現（即使沒有第二個優化步驟）： * 隱藏層的數量等于一 * 該層中的神經元數量是輸入和輸出層中神經元的平均值 然而，就像層數一樣，你可以嘗試逐漸增加神經元的數量，直到網絡開始過擬合。 ### 權重和偏置初始化 正如我們將在下一個示例中看到的那樣，初始化權重和偏置，隱藏層是一個重要的超參數，需要注意： * 不要做所有零初始化：一個聽起來合理的想法可能是將所有初始權重設置為零，但它在實踐中不起作用。這是因為如果網絡中的每個神經元計算相同的輸出，如果它們的權重被初始化為相同，則神經元之間將不存在不對稱的來源。 * 小隨機數：也可以將神經元的權重初始化為小數，但不能相同為零。或者，可以使用從均勻分布中抽取的小數字。 * 初始化偏差：通常將偏差初始化為零，因為權重中的小隨機數提供不對稱性破壞。將偏差設置為一個小的常量值，例如所有偏差的 0.01，確保所有 ReLU 單元都可以傳播一些梯度。但是，它既沒有表現良好，也沒有表現出持續改進因此，建議堅持使用零。 ### 選擇最合適的優化器 因為在 FFNN 中， 目標函數之一是最小化評估成本，我們必須定義一個優化器。我們已經看到了如何使用[`tf.train.AdamOptimizer`](https://www.tensorflow.org/api_docs/python/tf/train/AdamOptimizer)。[`Tensorflow tf.train`](https://www.tensorflow.org/api_docs/python/tf/train)提供了一組有助于訓練模型的類和函數。就個人而言，我發現 Adam 優化器在實踐中對我很有效，而不必考慮學習率等等。 對于大多數情況，我們可以利用 Adam，但有時我們可以采用實現的`RMSPropOptimizer`函數，這是梯度下降的高級形式。`RMSPropOptimizer`函數實現`RMSProp`算法。 `RMSPropOptimizer`函數還將學習率除以指數衰減的平方梯度平均值。衰減參數的建議設置值為`0.9`，而學習率的良好默認值為`0.001`： ```py optimizer = tf.train.RMSPropOptimizer(0.001, 0.9).minimize(cost_op) ``` 使用最常見的優化器 SGD，學習率必須隨`1/T`縮放才能獲得收斂，其中`T`是迭代次數。`RMSProp`嘗試通過調整步長來自動克服此限制，以使步長與梯度的比例相同。 因此，如果您正在訓練神經網絡，但計算梯度是必需的，使用`tf.train.RMSPropOptimizer()`將是在小批量設置中學習的更快方式。研究人員還建議在訓練 CNN 等深層網絡時使用動量優化器。 最后，如果您想通過設置這些優化器來玩游戲，您只需要更改一行。由于時間限制，我沒有嘗試過所有這些。然而，根據 Sebastian Ruder 最近的一篇研究論文（見[此鏈接](https://arxiv.org/abs/1609.04747)），自適應學習率方法的優化者，`Adagrad`，`Adadelta`，`RMSprop`和`Adam`是最合適的，并為這些情況提供最佳收斂。 ### 網格搜索和隨機搜索的超參數調整 采樣搜索的兩種通用候選方法在其他基于 Python 的機器學習庫（如 Scikit-learn）中提供。對于給定值，[`GridSearchCV`](http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html#sklearn.model_selection.GridSearchCV)詳盡考慮所有參數組合，而[`RandomizedSearchCV`](http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.RandomizedSearchCV.html#sklearn.model_selection.RandomizedSearchCV)可以從具有指定分布的參數空間中對給定數量的候選進行采樣。 `GridSearchCV`是自動測試和優化超參數的好方法。我經常在 Scikit-learn 中使用它。然而，`TensorFlowEstimator`優化`learning_rate`，`batch_size`等等還不是那么簡單。而且，正如我所說，我們經常調整這么多超參數以獲得最佳結果。不過，[我發現這篇文章對于學習如何調整上述超參數非常有用](https://machinelearningmastery.com/grid-search-hyperparameters-deep-learning-models-python-keras/)。 隨機搜索和網格搜索探索完全相同的參數空間。參數設置的結果非常相似，而隨機搜索的運行時間則大大降低。 一些基準測試（例如[此鏈接](http://scikit-learn.org/stable/auto_examples/model_selection/)）已經報告了隨機搜索的表現略差，盡管這很可能是一種噪音效應并且不會延續到堅持不懈的測試集。 ## 正則化 有幾種方法可以控制 DNN 的訓練，以防止在訓練階段過擬合，例如，L2/L1 正則化，最大范數約束和退出： * L2 正則化：這可能是最常見的正則化形式。使用梯度下降參數更新，L2 正則化表示每個權重將線性地向零衰減。 * L1 正則化：對于每個權重 w，我們將項`λ|w|`添加到目標。然而， 也可以組合 L1 和 L2 正則化以實現彈性網絡正則化。 * 最大范數約束：這強制了每個隱藏層神經元的權重向量的大小的絕對上限。可以進一步使用投影的梯度下降來強制約束。 消失梯度問題出現在非常深的神經網絡（通常是 RNN，它將有一個專門的章節），它使用激活函數，其梯度往往很小（在 0 到 1 的范圍內）。 由于這些小梯度在反向傳播期間進一步增加，因此它們傾向于在整個層中“消失”，從而阻止網絡學習遠程依賴性。解決這個問題的常用方法是使用激活函數，如線性單元（又名 ReLU），它不會受到小梯度的影響。我們將看到一種改進的 RNN 變體，稱為長短期記憶 （又名 LSTM），它可以解決這個問題。我們將在第 5 章，優化 TensorFlow 自編碼器中看到關于該主題的更詳細討論。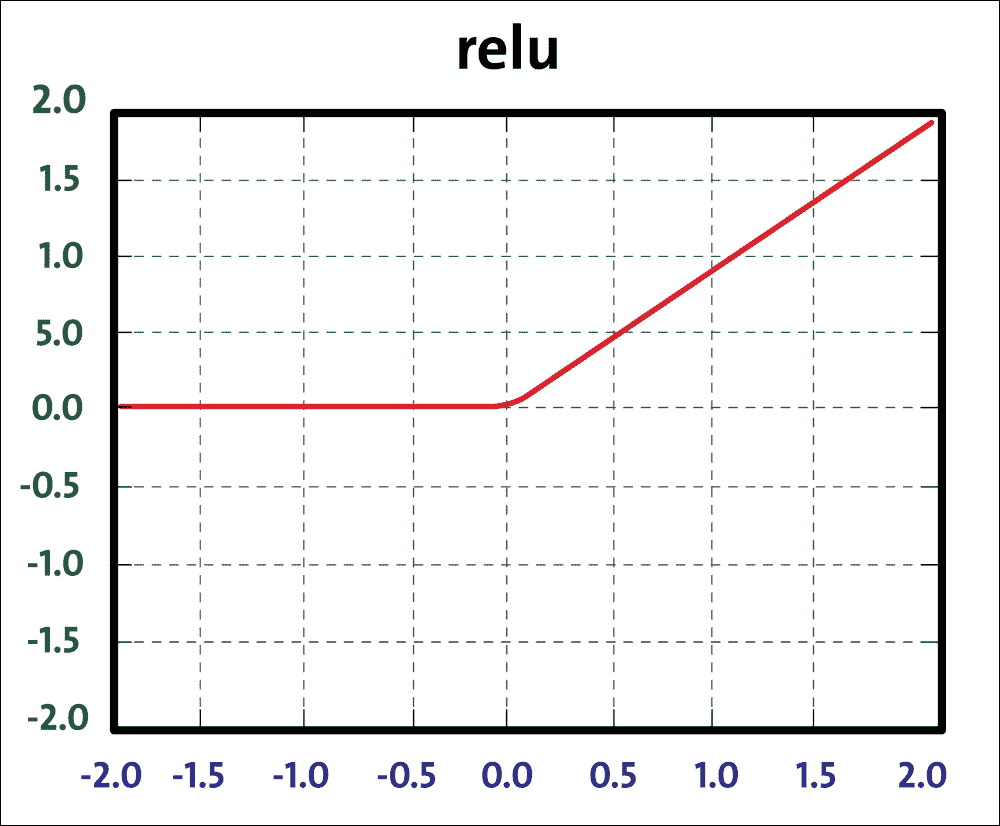 盡管如此，我們已經看到最后的架構更改提高了模型的準確率，但我們可以通過使用 ReLU 更改 sigmoid 激活函數來做得更好，如下所示：  圖 20：ReLU 函數 ReLU 單元計算函數`f(x) = max(0, x)`。 ReLU 計算速度快，因為它不需要任何指數計算，例如 sigmoid 或 tanh 激活所需的計算。此外，與 sigmoid/tanh 函數相比，發現它大大加速了隨機梯度下降的收斂。要使用 ReLU 函數，我們只需在先前實現的模型中更改前四個層的以下定義： 第一層輸出： ```py Y1 = tf.nn.relu(tf.matmul(XX, W1) + B1) # Output from layer 1 ``` 第二層輸出： ```py Y2 = tf.nn.relu(tf.matmul(Y1, W2) + B2) # Output from layer 2 ``` 第三層輸出： ```py Y3 = tf.nn.relu(tf.matmul(Y2, W3) + B3) # Output from layer 3 ``` 第四層輸出： ```py Y4 = tf.nn.relu(tf.matmul(Y3, W4) + B4) # Output from layer 4 ``` 輸出層： ```py Ylogits = tf.matmul(Y4, W5) + B5 # computing the logits Y = tf.nn.softmax(Ylogits) # output from layer 5 ``` 當然，`tf.nn.relu`是 TensorFlow 的 ReLU 實現。模型的準確率幾乎達到 98%，您可以看到運行網絡： ```py >>> Loading data/train-images-idx3-ubyte.mnist Loading data/train-labels-idx1-ubyte.mnist Loading data/t10k-images-idx3-ubyte.mnist Loading data/t10k-labels-idx1-ubyte.mnist Epoch: 0 Epoch: 1 Epoch: 2 Epoch: 3 Epoch: 4 Epoch: 5 Epoch: 6 Epoch: 7 Epoch: 8 Epoch: 9 Accuracy:0.9789 done >>> ``` 關注 TensorBoard 分析，從源文件執行的文件夾中，您應該數字： ```py $> Tensorboard --logdir = 'log_relu' # Don't put space before or after '=' ``` 然后在`localhost`上打開瀏覽器以顯示 TensorBoard 的起始頁面。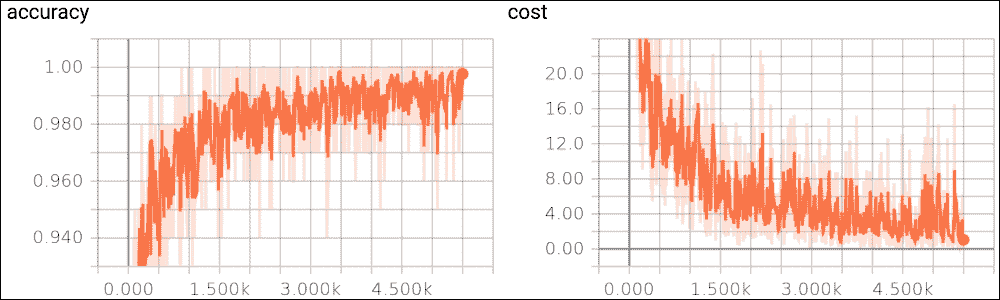在下圖中，我們顯示了趨勢對訓練集示例數量的準確率：  圖 21：訓練集上的準確率函數 在大約 1000 個示例之后，您可以很容易地看到在不良的初始趨勢之后，準確率如何開始快速漸進式改進。 ## 丟棄優化 在使用 DNN 時，我們需要另一個占位符用于丟棄，這是一個需要調整的超參數。它僅通過以某種概率保持神經元活動（比如`p > 1.0`）或者將其設置為零來實現。這個想法是在測試時使用單個神經網絡而不會丟棄。該網絡的權重是訓練權重的縮小版本。如果在訓練期間使用`dropout_keep_prob < 1.0`保留單元，則在測試時將該單元的輸出權重乘以`p`。 在學習階段，與下一層的連接可以限于神經元的子集，以減少要更新的權重。這種學習優化技術稱為丟棄。因此，丟棄是一種用于減少具有許多層和/或神經元的網絡中的過擬合的技術。通常，丟棄層位于具有大量可訓練神經元的層之后。 該技術允許將前一層的一定百分比的神經元設置為 0，然后排除激活。神經元激活被設置為 0 的概率由層內的丟棄率參數通過 0 和 1 之間的數字表示。實際上，神經元的激活保持等于丟棄率的概率；否則，它被丟棄，即設置為 0。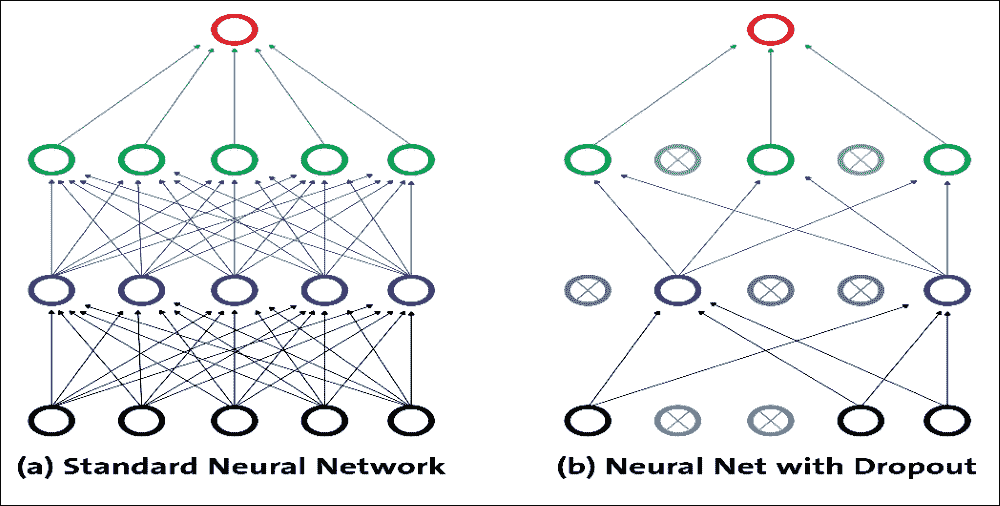  圖 22：丟棄表示 通過這種方式，對于每個輸入，網絡擁有與前一個略有不同的架構。即使這些架構具有相同的權重，一些連接也是有效的，有些連接不是每次都以不同的方式。上圖顯示了丟棄的工作原理：每個隱藏單元都是從網絡中隨機省略的，概率為`p`。 但需要注意的是，每個訓練實例的選定丟棄單元不同；這就是為什么這更像是一個訓練問題。丟棄可以被視為在大量不同的神經網絡中執行模型平均的有效方式，其中可以以比架構問題低得多的計算成本來避免過擬合。丟棄降低了神經元依賴于其他神經元存在的可能性。通過這種方式，它被迫更多地了解強大的特征，并且它們與其他不同神經元的聯系非常有用。 允許構建丟棄層的 TensorFlow 函數是`tf.nn.dropout`。此函數的輸入是前一層的輸出，并且丟棄參數`tf.nn.dropout`返回與輸入張量相同大小的輸出張量。該模型的實現遵循與五層網絡相同的規則。在這種情況下，我們必須在一層和另一層之間插入丟棄函數： ```py pkeep = tf.placeholder(tf.float32) Y1 = tf.nn.relu(tf.matmul(XX, W1) + B1) # Output from layer 1 Y1d = tf.nn.dropout(Y1, pkeep) Y2 = tf.nn.relu(tf.matmul(Y1, W2) + B2) # Output from layer 2 Y2d = tf.nn.dropout(Y2, pkeep) Y3 = tf.nn.relu(tf.matmul(Y2, W3) + B3) # Output from layer 3 Y3d = tf.nn.dropout(Y3, pkeep) Y4 = tf.nn.relu(tf.matmul(Y3, W4) + B4) # Output from layer 4 Y4d = tf.nn.dropout(Y4, pkeep) Ylogits = tf.matmul(Y4d, W5) + B5 # computing the logits Y = tf.nn.softmax(Ylogits) # output from layer 5 ``` 退出優化產生以下結果： ```py >>> Loading data/train-images-idx3-ubyte.mnist Loading data/train-labels-idx1-ubyte.mnist Loading data/t10k-images-idx3-ubyte.mnist Loading data/t10k-labels-idx1-ubyte.mnist Epoch: 0 Epoch: 1 Epoch: 2 Epoch: 3 Epoch: 4 Epoch: 5 Epoch: 6 Epoch: 7 Epoch: 8 Epoch: 9 Accuracy: 0.9666 done >>> ``` 盡管有這種實現， 之前的 ReLU 網絡仍然更好，但您可以嘗試更改網絡參數以提高模型的準確率。此外，由于這是一個很小的網絡，我們處理的是小規模的數據集，當您處理具有更復雜網絡的大規模高維數據集時，您會發現丟棄可能非常重要。我們將在下一章中看到一些動手實例。 現在，要了解丟棄優化的效果，讓我們開始 TensorBoard 分析。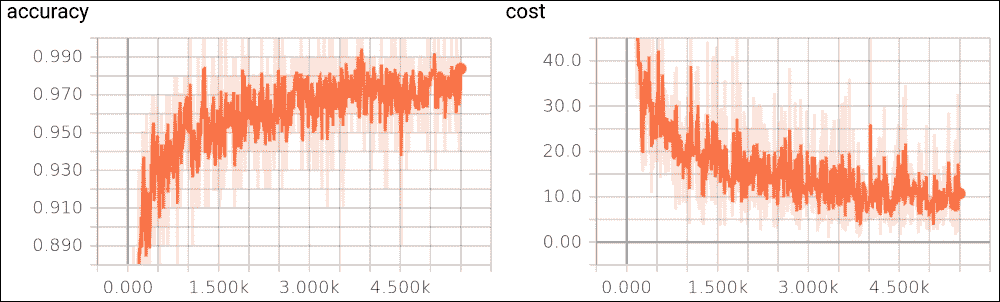只需鍵入以下內容： ```py $> Tensorboard --logdir=' log_softmax_relu_dropout/' ``` 下圖顯示了作為訓練示例函數的精度成本函數：  圖 23：a）丟棄優化的準確率，b）訓練集的成本函數 在上圖中，我們顯示成本函數作為訓練樣例的函數。這兩種趨勢都是我們所期望的：隨著訓練樣例的增加，準確率會提高，而成本函數會隨著迭代次數的增加而減 # 總結 我們已經了解了如何實現 FFNN 架構，其特征在于一組輸入單元，一組輸出單元以及一個或多個連接該輸出的輸入級別的隱藏單元。我們已經看到如何組織網絡層，以便級別之間的連接是完全的并且在單個方向上：每個單元從前一層的所有單元接收信號并發送其輸出值，適當地權衡到所有單元的下一層。 我們還看到了如何為每個層定義激活函數（例如，sigmoid，ReLU，tanh 和 softmax），其中激活函數的選擇取決于架構和要解決的問題。 然后，我們實現了四種不同的 FFNN 模型。第一個模型有一個隱藏層，具有 softmax 激活函數。其他三個更復雜的模型總共有五個隱藏層，但具有不同的激活函數。我們還看到了如何使用 TensorFlow 實現深度 MLP 和 DBN，以解決分類任務。使用這些實現，我們設法達到了 90% 以上的準確率。最后，我們討論了如何調整 DNN 的超參數以獲得更好和更優化的表現。 雖然常規的 FFNN（例如 MLP）適用于小圖像（例如，MNIST 或 CIFAR-10），但由于需要大量參數，它會因較大的圖像而分解。例如，100×100 圖像具有 10,000 個像素，并且如果第一層僅具有 1,000 個神經元（其已經嚴格限制傳輸到下一層的信息量），則這意味著 1000 萬個連接。另外，這僅適用于第一層。 重要的是，DNN 不知道像素的組織方式，因此不知道附近的像素是否接近。 CNN 的架構嵌入了這種先驗知識。較低層通常識別圖像的單元域中的特征，而較高層將較低層特征組合成較大特征。這適用于大多數自然圖像，與 DNN 相比，CNN 具有決定性的先機性。 在下一章中，我們將進一步探討神經網絡模型的復雜性，引入 CNN，這可能對深度學習技術產生重大影響。我們將研究主要功能并查看一些實現示例。